Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.

388
CHAPTER
8.
ELEMENTS
OF
STRUCTURAL
GEOLOGY
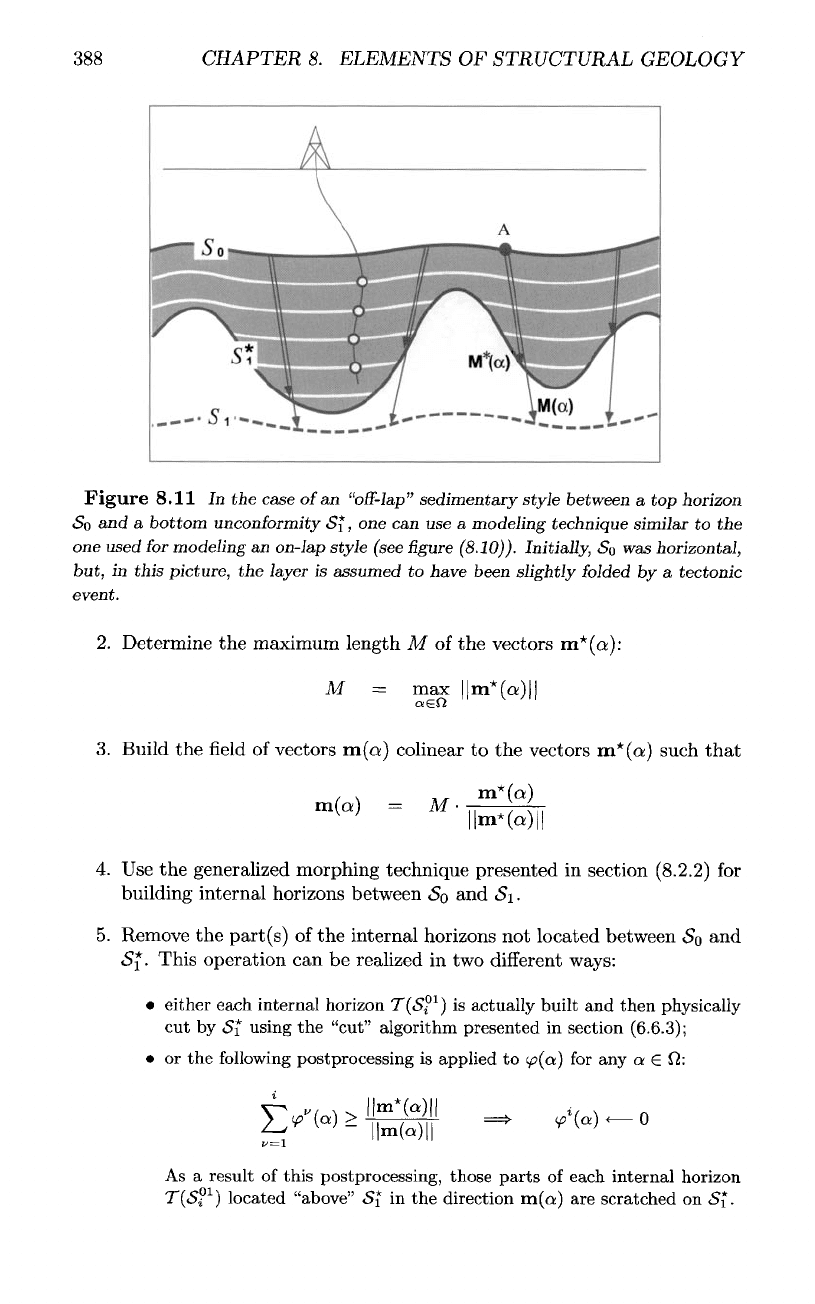
Figure
8.11
In the
case
of an
"off-lap"
sedimentary style between
a top
horizon
(So
and a
bottom
unconformity
<Sjf,
one can use a
modeling technique similar
to the
one
used
for
modeling
an
on-lap
style (see
figure
(8.10)).
Initially,
So was
horizontal,
but,
in
this picture,
the
layer
is
assumed
to
have been slightly
folded
by a
tectonic
event.
2.
Determine
the
maximum
length
M
of the
vectors
m*(a):
3.
Build
the field of
vectors
m(a)
colinear
to the
vectors
m*(ct:)
such
that
4.
Use the
generalized
morphing
technique
presented
in
section
(8.2.2)
for
building
internal
horizons
between
<S
0
and
Si.
5.
Remove
the
part(s)
of the
internal
horizons
not
located
between
<S
0
and
$i.
This
operation
can be
realized
in two
different ways:
•
either each
internal
horizon
T(5°
1
)
is
actually
built
and
then
physically
cut by
<Si
using
the
"cut" algorithm presented
in
section (6.6.3);
• or the
following
postprocessing
is
applied
to
if>(oi)
for any a £
fi:
As
a
result
of
this postprocessing, those
parts
of
each internal horizon
T(Sf
l
)
located "above"
<Si
in the
direction
m(o;)
are
scratched
on
<Si.

8.2.
MODELING
STRATIFIED
MEDIA
389
Off-lap
style
The
on-lap
sedimentary style presented above
was
justified
by the
fact
that
the
bottom
of the sea at the
time
of
sedimentation
was
sub-horizontal.
As
shown
in
figure
(8.11), there
are
cases where this hypothesis
is
untrue
and the
sedi-
mentation progrades
on a
preexisting
relief
corresponding
to an
unconformity
on
which
the
sediments stack more
or
less horizontally.
Such
a
sedimentation style
is
called
the
"off-lap"
style and,
as
suggested
in
figure
(8.11),
the
same modeling technique
as the one
used
for
modeling
the
on-lap style
can be
used:
the
roles
of
SQ
and
Si
have merely
to be
permuted.
8.2.7
Building
a
3-grid
by
extrusion
of a
2-grid
Any
regular
or
irregular 2-grid
denned
on the
bottom horizon
of a
layer
can
be
transformed into
a
(regular
or
irregular) 3-grid
by
extrusion along
the
morphing
vectors
that
bridge
the top and
bottom horizons
of the
layer.
For
that
purpose,
it is
sufficient
to
proceed
as
follows
for
each
2-cell
C
2
located
on
the
bottom horizon:
•
Determine
the
location
on the
bottom
horizon
of the
vertices
{x^
: i —
1,2,...,
N(C
2
}}
of C
2
and
interpolate
the
associated
morphing
vector
m(xi)
and the
local
relative
thickness
function
v?(xj)
at
these
locations.
• For
each
integer
j
belonging
to the
range
{0,
n},
build
the
2-cell
C
2
(j)
whose
vertices
Xi(j')
are
defined
by
• For
each
pair
of
2-cells
(C
2
(j),
C
2
(j
—
1)),
build
an
associated
cylindrical
3-cell
C
3
(j)
whose
top and
bottom
are
identical
to
C
2
(j
—
1) and
C
2
(j),
respectively.
The
process
so
defined
for
transforming
a
2-grid into
a
3-grid
is
called "ex-
trusion".
Such
a
process
can be
applied whether
the
initial 2-grid
is
regular
or
irregular.
On
page 133,
figure
(3.23) shows
an
example
of
irregular 3-grid
built
by
extrusion
of an
irregular 2-grid.
8.2.8
Curvilinear morphing
So
far,
for the
sake
of
simplicity,
the
concept
of
morphing
was
based
on a
family
of
morphing vectors
attached
to the
nodes
of a
triangulated
surface
T(So).
In
practice,
these
vectors
can be
replaced
by a
family
of
curves
{m(s|o:)
: a 6
f2}
joining
the
nodes
of the
bottom surface
T(So)
to the top
surface
Si
and
such
that
s
represents
the
curvilinear abscissa
on
these curves oriented
from
T(So)
to
Si.
If
the
curves
{m(s|o;)
: a
e
0}
so
defined
are
given, then
the
concept
of
morphing
introduced
in the
previous sections
can be
adapted
as
follows
to
define
a
Curvilinear morphing:
•
interpret
each
curve
m(s a) as a
"morphing
curve,"
and
note
m(si\a)
the
intersection
of
this
curve
with
the
ith
sub-horizon
T(5j
01
);
7
8

390
CHAPTER
8.
ELEMENTS
OF
STRUCTURAL
GEOLOGY
•
interpret
the
component
<p
l
(a)
of the
relative
thickness
function
as the
pro-
portion
of the
curve
m(s|a)
comprised
between
the
sub-horizons
T(«S°1
1
)
and
T^
01
):
Proceeding this
way
allows
the
node
XJ(Q)
of the
sub-horizon
T(Sf
l
)
to be
denned
as
follows:
On
page 122,
figure
(3.17) shows
an
example
of a
regular 3-grids built
by
curvilinear extrusion
of a
regular 2-grid.
8.3
Merging
seismic
data
with
well
data
Most
of the
time,
a first
draft
S*
of an
(unknown) geological horizon
5 is
modeled
from
seismic
data.
It is
necessary
to
merge this
first
draft with well
data
to
obtain
a
better
approximation
S**
closer
to S.
As
suggested
in figure
(8.12), "well-markers"
{wi,w
2
,...}
correspond-
ing
to the
intersections
of the
well-paths with
the
actual horizon
<S
provide
sparse,
but
accurate,
information
on the
shape
of
<S.
Conversely,
the
seismic
data
provide dense information
on the
shape
of
S]
however,
in
general, such
information
is
biased
due to
errors
in the
modeling
of
seismic velocities used
for
building
«S*.
Therefore,
in
general,
S*
does
not
honor
the
well-markers;
to
each marker
Wj
can be
associated
a
"discrepancy" vector
dj,
as
defined
by
dj
=
Wi
—
w*
In the
above definition,
w* is the
point
of S*
that
should
be
coincident with
Wi
if
there were
no
error.
If the
seismic information
was
coherent with
the
well-markers,
the
discrepancy vectors
{dj}
should
all be
equal
to
zero.
Unfor-
tunately,
as
suggested
in figure
(8.12), this
is
generally
not the
case,
so it is
necessary
to
look
for a
technique
to
reconcile
these
two
sources
of
data.
For
this purpose,
it is
assumed below
that
• S* is
approximated
by a
triangulated
surface
T(<S*);
• the
geometry
of S* is
denned
by the set of
vectors
(x*(a)
: a
G
£1}
corre-
sponding
to the
location
of the
vertices
of
T(«S*).
8.3.1
A first
approach
Determining
the
observed
discrepancies
{dj}
Assuming
that
S*
is not too far
from
the
actual
horizon
S
implies
that
the
discrepancies
d(a)
for all the
nodes
of
<S*
must
be
small.
In
particular, each
observed discrepancy
dj
must
be as
small
as
possible, implying
that
we
should
have
11
is
minimal
11
This
implication
is a
direct consequence
of the
orthogonal projection theorem
[141].

8.3. MERGING
SEISMIC
DATA WITH WELL DATA
391
Figure
8.12
Cross
section
showing
the
discrepancies
{di}
observed
between
a
seismic
horizon
<S*
and a
series
of
well-markers
{Wj}.
^=>-
w*
=
point
of S*
closest
from
Wj
•<=>•
di
orthogonal
to
<S*
Adopting
this
model
for the
direction
of the
discrepancy makes
it
easy
to
compute
the
observed discrepancies
{dj}
thanks
to the
following
algorithm:
let
P(S*)
be a
dense
set of
points
covering
S*
for_all(
well-marker
Wi ) {
•
look
for w*
€
P(S*)
such
that
||wi-w*||
=
min
w
*
e
p
(<
s*)
||wi
-
w*||
•
compute
di = (wi
—
w*)
}
The
model proposed above
for
determining
the
observed discrepancies
{d^}
has the
advantage
of
being simple,
but it
does
not
take into account
the
origin
of
the
discrepancies.
If
need
be, as
proposed
in
[49],
it is
possible
to
adapt
the
above algorithm
to
take into account cases where
the
direction
of
d;
depends
both
on the
geometry
of S* and on the
model describing
the
variations
of the
seismic
velocity used
for
building
the
initial
surface
<S*.
Removing
the
discrepancies
The
discrepancies between
<S*
and
<S
can be
removed easily once
the
discrep-
ancy
d(a)
is
known
at
each node
a of the
initial triangulated
surface
T(«S*).
In
this
case,
it
suffices
to
build
an
improved solution
T(e>**)
whose vertices
have
a
location
x**(a)
deduced
as
follows
from
the
location
x*(a)
of
each
node
a of
T(5*):

392
CHAPTER
8.
ELEMENTS
OF
STRUCTURAL
GEOLOGY
The
three components
of the
discrepancy
are
considered
as
fuzzy
Control-
Properties
to be
interpolated
from
the
initial observed discrepancies.
For
this
purpose,
two
different
techniques
can be
used:
• The first
technique
consists
of
attaching
each
observed
discrepancy
di
to its
associated
point
Wj
and
interpolating
these
discrepancies,
with
DSI
on
T(S*)
directly.
•
Most
of the
time,
T(S*}
is not
unique
and,
in
fact,
a
series
{Tj(S*}}
of
triangulated
surfaces
needs
to be
reconciled
with
the
well
data.
In
such
a
case,
the
full
set of
discrepancies
observed
on the
series
{7}(<S*)}
must
be
globally
interpolated
with
DSI on a
regular
3-grid
covering
the
studied
domain.
For
each
node
QLJ
of a
particular
surface
T,
(»$*),
the
associated
discrepancy
d(aj)
can
then
be
interpolated
from
values
of the
discrepancy
attached
to the
neighboring
nodes
of the
3-grid.
8.3.2
A
second approach
Let
us
assume
that
the
surface
to be
modeled
is
embedded
in a
domain
of the
3D
space covered
by a 3D
seismic survey.
The
basic idea behind
the
method
proposed
in
this section
is
that
the
seismic
data
provide
the
correct shape
of
the
horizons while
the
well
data
provide
the
correct location
of
these horizons.
From
the 3D
seismic survey,
and for any
location
x in the
studied domain,
it is
possible
to
build
a
field
of
vectors
n(x)
approximately orthogonal
to the
geological
horizons.
It
makes sense
to use
this
field of
vectors
for
controlling
the
shape
of the
triangulated
surface
T(<S*)
corresponding
to the
horizon
to be
modeled.
In
practice,
the
discrete model
A'f
3
(0,
N,
x,C
x
)
associated
12
with
T(S]
can be
constrained
in
such
a way
that
• for
each
well-marker
Wj,
a
"Control-Node"
or a
"fuzzy
Control-Point"
con-
straint
(see
page
263)
specifying
that
T(S*}
must
interpolate
Wj
is
added
to
Cx;
• for
each
node
a £
fJ,
a
"Control-Parallelism"
constraint
(see
page
268)
speci-
fying
that
is
added
to
Cx-
This modeling technique
is
particularly
efficient.
At the
extreme,
as
shown
in
figure
(6.9),
it is
even possible
to
model
an
anticline when only
one
well-marker
is
given.
8.4
Deformation analysis
The
analysis
of the
deformations
of
geological surfaces
and
volumes through-
out
geological time plays
a
central role
in
structural geology. This section
shows,
in a
concise
and
unified
way,
how to
characterize these deformations
using
a
differential
geometry approach. Applications
of
such
a
characteriza-
tion
will
be
presented
in
sections
(8.5)
and
(8.6).
12
See
definition, page
246.

8.4.
DEFORMATION ANALYSIS
Figure
8.13
Displacement
and
deformations
of
a
region
71
through time.
8.4.1
Notations
By
definition,
a
parametric representation
of a
volume
V or,
more simply,
a
parametric volume,
is the
name given
to any
continuously twice
differentiable
mapping
x
from
a 3D
parametric domain
D
onto
V:
As
can be
seen, this definition generalizes
the
definitions (5.1)
and
(5.10) given
for
parametric curves
and
surfaces.
For the
sake
of
generality,
these
definitions
can
be
unified
by
introducing
an
n-dimensional
parameter
u
belonging
to an n-
dimensional
parametric
domain
D and by
defining
a
parametric
representation
x(u)
of an
n-dimensional region
7£
as
follows:
In
geological applications,
K
belongs
to the 3D
space
and
x(u)
has
three
components
that
can be
noted
in any of the
following
ways:
We
will
assume
that
x is
twice continuously derivable relative
to
u
1
.
Further-
more,
we
will
use the
following
notations
similar
to
those
used
in
chapter
5
for
parametric curves
and
surfaces:
In
practice,
• if n = 1,
then
7£
is a
parametric
curve;
• if n = 2,
then
~R,
is a
parametric
surface;
• if n = 3,
then
JL
is a
parametric
volume.
393

394
CHAPTER
8.
ELEMENTS
OF
STRUCTURAL GEOLOGY
Thanks
to
these
unified
notations,
no
distinction
is
made below between
curves,
surfaces
and
volumes.
As
shown
in figure
(8.13),
we
consider
a
con-
tinuum
of
material points
that,
at
initial time
t = 0 fills the
region
7£[o]
and,
at final
time
t fills the
region
'R,.
To
describe
the
motion
of a
point
x, we
consider
the
frame
(Ui,...,
U
n
),
which moves through time with
the
medium
and is
defined
as
follows:
The
components
{g
u
i
u
j}
of the
metric tensor associated with
7£
are
stored
in
an (n x
n)
symmetric matrix
G,
as
defined
by
Similarly,
the
components
{(g^u^lo}}
°f the
metric tensor associated with
7£[o]
are
stored
in an (n x n)
symmetric matrix
G^
and are
defined
by
The
coordinates
of any
point
of
7£
relative
to
this
frame
do not
change through
time
so
that
the
vector
cbcjo]
observed
at
initial time
t = 0 is
transformed into
a
vector
cbc
at
time
t
such
that
As
will
be
shown
in the
next sections,
by
comparing
|
dx[o]||
and |
dx.
|, the
deformation
of the
region
7£
through time
can be
characterized.
8.4.2 Strain
tensor
and
notion
of
dilatation
As
shown
in figure
(8.13),
a
pair
of
twin regions
7£[
0
]
and
71
corresponds
to the
same
set of
points
before
and
after
deformation.
As can be
seen
in
this
figure,
any
infinitesimal
step
dx[
0
]
G
7£[o]
is
transformed into
a
twin
step
dx
e
7£.
According
to
equations (8.19),
(8.20)
and
(8.21),
it
should
be
noted
that
the
(contravariant) components
{du
1
}
of
these vectors
are the
same,
but
their
lengths
may be
different:
In the
mechanics
of
continuous media
(e.g.,
see
[205,
198]),
"covariant
Strain
tensor"
is the
name given
to the
(twice covariant) tensor whose components

8.4.
DEFORMATION ANALYSIS
{£
u
i
u
j}
relative
to the
frame
{Ui,...,
U
n
}
are
stored
in the
(n
x
n)
symmetric
matrix
£,
as
defined
by
13
Using
this
definition
of
£,
it may be
noted
that
the
variations
of the
square
length
of the
segment having (contravariant) components
{du
1
}
is
such
that
It is
also interesting
to
evaluate
the
variation
of the
(Lebesgue) measure
of
the
region element
G?7£[o]
when transformed into
dTZ.
As
with equation (5.19),
it
can be
shown
that
By
definition,
one
calls "dilatation"
the
coefficient
9 as
defined
by
Prom equations
(8.24),
it is
easy
to
show
that
the
coefficient
0 so
defined
can
be
deduced
from
the
metric tensors
G^
and G as
follows:
In
practice,
as
shown
in figure
(8.22)
this parameter
can be
displayed
in
7£
to
point
out the
variations
of the
deformations.
8.4.3 Principal
strains
Any
vector
W
located
in the
region
72.
can be
written
as
Let
us now
consider
a
unit
vector
W in the
region
72.;
according
to
(8.27)
and
(8.19),
such
a
vector
is
characterized
by
If
the
increment
dx.
is
chosen
as
being colinear
to W
13
Note
that
the
coefficient
|
used
in
the
definition
of
S
plays
no
role
in
this book
a
introduced
to be
consistent with traditional notations used
in the
mechanics
of
continuous
media.
395

396
CHAPTER
8.
ELEMENTS
OF
STRUCTURAL GEOLOGY
then
the
strain
A(W)
in the
direction
W
between
the
initial
state
7£[oj
and
the final
state
7£
is
denned
by
Prom
equations (8.23)
and
(8.28),
it can be
seen
that
(8.29)
is
equivalent
to
the
following
system
of
equations:
According
to the
Lagrange multiplier technique [141,
90,
163],
the
extremum
values
of
A(W)
honoring equations (8.30)
are
those
for
which
the
derivatives
of
the
following
function
C(W,
A)
vanish:
From equations (8.30)
and
using
the
vectorial derivations rules
(4.26),
it can
be
deduced
that
the
optimum values
of
A(W.)
must honor
the
following
equa-
tion:
In
other words,
the
optimum directions
of W are
characterized
by the
follow-
ing
equation:
Introducing
the
(n
x
n)
matrix
S as
defined
by
it
can be
noted
that
equation (8.31)
can
also
be
written
as
follows:
Prom equations (8.31), (8.32),
and
(8.33),
it can be
deduced
that
W =
W
(i)
corresponds
14
to an
optimum
of
A(W)
if, and
only
if, his
associated
column
matrix
W^
is an
eigen direction
of S:
Combining
this equation with system (8.30) makes
it
possible
to see
that
the
eigen
value
A^)
associated with
the
eigen direction
W^
is
equal
to the
value
of
such
an
optimum:
From
equations (8.33)
and
(8.34),
the
following
conclusions
can be
made:
14
Subscripts
in
parentheses
are
used
to
avoid confusion with (covariant) indices
of the
components
of
vectors.

8.4.
DEFORMATION ANALYSIS
• The
function
A(W)
has n
extrema
corresponding
to the
unit
vectors
(W(i)}
colinear
to the
vectors
(D^)}
associated
with
the n
eigen
directions
{D^}
of
S as
follows:
• The
eigen
values
(A(j)
: i =
l,...,n}
of S
associated
with
the
directions
(W(i)
: i =
1,...,
n}
are
such
that
From equations (8.36)
and
(8.29),
it can be
easily
verified
that
the
eigen values
{X(i)}
defined
above
are
such
that
By
definition,
these eigen values
(A(^)
: i =
1,..
.,n}
are
called
the
"principal
strains"
and the
associated unit vectors
{W(^
: i =
1,..
.,n}
are
called
the
"principal
strain
directions."
It
will
be
shown
in the
next
section
that
the
vectors
{W(^}
so
defined
are
orthogonal.
The
"elongations"
{e^}
associated with these directions
are
defined
by
From equations (8.36)
and
(8.37)
and
from
the
definition
(8.29)
of
A(W
W
),
it
can be
checked
that
these elongations
are
such
that
Note that,
from
definition (8.38),
it can be
deduced easily
that
Moreover,
it can be
deduced
from
equation (8.37)
that
the
elongations
so
defined
are
such
that
8.4.4
Orthogonality
of the
principal strain directions
It can be
observed
that
the
principal strain directions
are
intrinsic properties
independent
of the
parameterization
of
*R,
or
7£[
0
].
Consequently, without loss
of
generality,
it can
always
be
assumed
that
and, according
to
equation (8.32),
the
matrix
S
then reduces
to
397
