Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.


368
CHAPTER
7.
CURVILINEAR TRIANGULATED SURFACES
Figure
7.24
Modeling variable sharpness creases.
(A)
Initial
mesh
representing
a
cube.
(B)
Limit
surface
without
crease.
(C, D) The
edges
of the top and
bottom
faces
have been
set as
increasing sharp creases.
(E) The
edges
of
the top and
bottom
faces
have been
set as
infinitely sharp creases.
(F)
Limit
surface
obtained
for
another
set of
edges tagged
as
infinitely sharp creases.
where
|AT
0
(o;)|
is the
number
of
nodes surrounding
the
node
a.
Whatever
the
technique used
for
determining
the
angles
of the
triangles
DT((X,
ai,
a<2)
in the
parametric domain,
the
DSI
weighting
coefficients
v(a,
/3)
can
then easily
be
determined.
For
example,
as
suggested
in figure
(7.23),
if
a is an
internal node, then
In the
above equation,
$~(a,/3)
and
$
+
(a,/3)
represent
the
angles opposite
to the
edge
E(a,(3],
while
|-D(a;)|
represents
the sum of the
area
of all the
triangles surrounding
the
node
a.
In
differential
geometry
[61],
the
local mapping
of a
surface
on its
tangent
plane
is
called "exponential
map."
For
this reason,
it is
proposed
to
call
"exponential
map
weightings"
the
coefficients
{v(a,/3}}
defined
by
equation
(7.47).
Modeling
creases
of
variable
sharpness
As
illustrated
in figure
(7.24),
it is
easy
to
model
creases
of
variable
sharpness
by
modulating
the
{v(a,
(3)}
coefficients
used
to
define
the
local
DSI
roughness
at
node
a
(see equations
(4.7),
and
(7.43)).
A
crease
is
defined
to be a set of
vertices
C
connected
by a set of
edges
of the
initial triangulation,
defining
a
polygonal curve
on the
surface
to be
modeled. Each crease
is
provided with
an
associated nonnegative
coefficient
called
the
"sharpness factor,"
and the
new
coefficients
{^(a,/?)}
to be
applied
to a
vertex
a
when introducing
a

7.5.
CONCLUSIONS
crease
C
have then
to be
defined
as follows
(see
[132]):
7.5
Conclusions
In
this chapter
it has
been demonstrated that,
from
a
theoretical point
of
view,
it is
possible
to
build
a
smooth
G
1
triangulated surface consisting
of a
patchwork
of
parametric curvilinear Gregory triangles. Compared
to
linear
triangles
(see
section
(6.1.2)),
curvilinear triangles
on
average require nine
additional Control-Points.
As can be
imagined,
the
number
of
additional
Control-Points
needed
to
ensure
a
G
2
continuity would
be
considerably
higher,
making
the use of
such
an
approach
in
real applications unreasonable.
An
interesting alternative
to
these parametric models
of
curvilinear trian-
gulated surfaces consists
in
subdividing recursively linear triangles into smaller
triangles whose geometry
is
computed
to
approximate
a
smooth
G
2
solution.
As
shown
in figure
(7.16),
such
an
approach
is
very
efficient
and can
reasonably
compete with parametric methods. Moreover,
the
rich
set of
DSI
constraints
described
in
chapter
6 is
still applicable
and is
important
to
consider
from
a
practical point
of
view.
369
This page intentionally left blank

Chapter
8
Elements
of
Structural
Geology
Until
now in
this book,
surfaces
and
volumes have been considered
from
a
static
point
of
view without taking
into
account
the way
they were generated.
As a
consequence, most
of
the
modeling techniques presented
in the
previous
chapters
have
a
wide scope
of
applications
that
goes
far
beyond
the
limited
domain
of
the
geosciences
and
that potentially
can be
applied
to the
modeling
of
any
natural object.
In
geology, faults
and
horizons have evolved
differently
through geological time: this chapter
will
show
that
these
different
cinematic
behaviors
have
a
strong
influence
on
their shape
and
properties.
8.1
Geometry
of
faults
and
horizons
8.1.1 Modeling faults
In
the
modeling process
of the
subsurface, horizons
and
faults
are
both mod-
eled
as
triangulated surfaces. However,
it is
easy
to see
that
any one
surface
does
not
necessarily represent
a
real fault surface because
the two
fault blocks
on
both
sides
of the
fault surface have
to
slide
one on the
other while keeping
contact. Assuming
that
fault
blocks
are
rigid
and
remain
in
contact during
the
faulting process implies
that
the
fault
surface must necessarily belong
to
a
specific
kind
of
surface [128,
216].
For
example, planes, spheres, cylinders
and
surfaces
of
revolution
are
admissible examples
of
fault surfaces, while
an
egg-box surface
is
not. More generally, even though
the
pair
of
fault
blocks
adjacent
to a
fault
surface does
not
remain rigid during
the
faulting process,
it is
easy
to
understand
that
the
geometry
of the
associated
fault must obey
371

372
CHAPTER
8.
ELEMENTS
OF
STRUCTURAL GEOLOGY
Figure
8.1
Displacement
of
fault
blocks
along
a
fault
surface
F:
the
fault
surface
is
tangent
everywhere
to a field
of
unit
fault-throw
directions
(t(x)
: x €
f}
attached
to
F
and
defining
the
local
direction
of
the
displacement.
The
fault-throw
directions
and the
associated
fault-striae
are
drawn
in
white
in
part
(A).
The
schema
in
part
(B)
shows
that,
in the
case
of
a
ruled
surface,
t(x)
is
parallel
to the
direction
of
minimum
absolute
normal
curvature.
certain laws
to
allow
the
adjacent fault blocks
to
slide
on
each
other.
This section begins
by
presenting
an
intrinsic property
of
faults
and
then
shows
how
this characterization
can be
used
to
build
a
DSI
constraint
specific
to
faults.
For the
sake
of
simplicity,
the
fault
T
to be
modeled
is
assumed
to
be
approximated
by a
triangulated
surface
T^)
associated
with
a
discrete
model
A^
3
(ri,
JV,
x,C
x
),
where
(x(a)
: a G
17}
corresponds
to the
locations
of
the
vertices
of
T(J
7
)
in the 3D
space.
Fault characterization
As
suggested
in figure
(8.1),
let us
assume
that
the two
fault
blocks
on
both
sides
of a
fault
J-
have slid along
F.
The
direction
of
such
a
relative displace-
ment
can be
modeled
as a field of
unit fault-throw directions
t(x)
defined
at
each point
x on
J-.
Geologists
can
sometimes observe curves, called "fault-
striae," engraved
on
F
and
tangential everywhere
to
these throw vectors
(see
figure (8.1)-A).
In
the
specific
case where
F
is a
ruled surface with undulations similar
to
those represented
in figure
(8.1)-B,
it is
clear
that
these undulations directly
control
the
fault-throw directions
t(x).
More precisely,
in
this
particular case,
at any
location
x G
J-
where
the
undulations
are
sufficient
for
inducing prin-
cipal
curvatures
1
ki
(x) and
k%
(x)
such
that
it
can be
observed
that
t(x)
must
be
constant
and
parallel
to the
direction
1
See
page
213:
it is
assumed that
|fci(x)|
<
|fc2(x)|.

8.1.
GEOMETRY
OF
FAULTS
AND
HORIZONS
373
tram
(
x
)
°f
minimum
absolute
normal
curvature
2
as
defined
by
In
the
general case where
f
is not
necessarily
a
ruled surface,
let us
consider
the
subset
F(X)
of
T
denned
as a
function
of the
threshold
A > 0 as
follows:
To
allow adjacent
fault
blocks
separated
by
F
to
slide
on
each other,
it can
reasonably
be
conjectured
that,
at
each location
x 6
^(A),
the
fault-throw
direction t(x) must
be
parallel
to the
direction
of the
minimum absolute
normal curvature
t
min
(x)
as
defined
by
equation
(8.2).
Accordingly,
at any
location
x G
.F(A),
it is
proposed
to
define
the
notion
of
fault-throw direction
as
follows:
In the
following,
to
remove
the
ambiguity introduced
by the
multiplying factor
(±1), t(x)
is
assumed
to be
chosen
in
such
a way
that
its z
component
t
z
(x)
is
positive:
Let
N(x)
be the
unit normal vector
to
T
at
location
x £
J-.
It can be
observed
that
the
projection
projp(v)
of the
vertical unit vector
v =
[0,0,1]*
on the
tangent
plane
of
f
at
location
x is
such
that
In
practice, fault-throw directions
are
seldom horizontal. Using
a
second
threshold
9 G [0,
Tr/2],
this observation leads
us to
introduce
the
subset
,F(A,
0)
of
.F,
defined
as
follows:
In
other words, fault-throw directions t(x)
that
make
an
angle greater than
9
with
projf(v}
are
excluded
from
^-"(A,
0).
Filtering
the field of
fault-throw
directions
In
practice, geological faults
are
modeled
from
seismic data, which
are
known
to be of
poor quality
in the
neighborhood
of
faults.
As a
consequence,
the
geometry
of
faults
is
generally
not
very precise [127]
and the field of the
fault-
throw directions
defined
above must
be filtered to
reduce
the
influence
of the
modeling errors.
For
this
purpose,
the
following
procedure
is
proposed:
•
Build
a
discrete model
_M
3
(O,7V,
t,C^)
associated with
the
same nodes
as.M
3
(ft,Ar,x,Cx).
• For
each node
a G 0:
2
It is
assumed
that
ti(x)
corresponds
to fci(x)
while
t2(x)
corresponds
to
/C2(x).

374
CHAPTER
8.
ELEMENTS
OF
STRUCTURAL
GEOLOGY
Figure
8.2 An
example
of
computed fault-throw directions
and
fault-striae
on a
given
fault
J-:
(A)
Initial
set
J-(X,
9} of
directions
of
minimum
curvature.
(B)
Filtered fault-throw directions.
(C)
Fault-throw direction extracted
from
the
earthquake
focal
mechanism.
(D)
Computed fault-striae.
In
this example,
theta
was
taken
equal
to
Tr/2.
—
use the
algorithm
described
on
page
228 for
estimating
the
principal cur-
vatures
/ci(x(a))
and fc2(x(a)) and
their associated directions
ti(x(a))
and
t2(x(a));
—
if
x(a)
£
JF(A,
0),
then
add a
fuzzy
Control-Node constraint
c =
C(OL)
to
C-£
specifying
that
t(a)
should
be
equal
to the
vector
denned
by
equations
(8.2),
(8.4),
and
(8.5) with
a
certainty
factor
w
c
as
defined
by
In the
above
definition
of
w
c
,
<p(\x
) is
assumed
to be a
positive increasing
function
of \x
that
vanishes
for \x = 0.
• Run
DSI
on
Ai
3
(ft,
TV,
t,
C
t
)
The
modulation
of the
certainty
factor
in
function
of the
absolute
difference
|fci(x(o:))
—
/c
2
(x(a))|
allows
consideration
of the
fact
that,
when
ki(x.(o))
is
close
to
A/2(x(a)),
the
direction
t(a)
can no
longer
be
considered
as
defining
the
fault-throw
direction.
In
practice,
it can be
observed
experimentally
that
this
filtering
algorithm
is
very efficient
and
generally
produces
results
consistent
with
geological
ob-
servations
as
long
as the
fault
model
is not too far
from
its
correct
geometry.

8.1.
GEOMETRY
OF
FAULTS
AND
HORIZONS
Figure (8.2) shows
an
example
of
fault-throw directions
filtered
using this
method:
the
surface
represented
in
this
figure
corresponds
to the
"North-
Ridge"
fault
in Los
Angeles,
and the
model built with gOcad
was
provided
by
the
Structural Geology group
in
Princeton.
A
strong similarity between
figure
(8.2)-B
showing
the
computed fault-throw directions
and
figure
(8.2)-C
corresponding
to a
direct determination
of
these vectors
by
structural geolo-
gists (courtesy
of S.
Carena) using
the
earthquakes
focal
mechanism
3
can be
observed.
Note
that
the
vectors displayed
in
figure
(8.2)-A
look erratic compared
to
the
result
of
their interpolation displayed
in
figure
(8.2)-B.
This smoothing
effect
is
mainly
due to the
fact
that
the
inital vectors
in
figure
(8.2)-A
are
weighted
by
certainty factors
w
c
as
defined
by
equation
(8.7).
Practical
remarks
Computed fault-throw directions cannot
be
used
in a
blind
way
without con-
sideration
of the
context,
and the
geologist
has to
decide whether these direc-
tions
are
relevant;
for
example:
• Due to
measurement
errors,
the
fault
model
F
may be too far
from
its
cor-
rect
geometry
and
then
produce
an
inconsistent
set of
fault-throw
directions
?(\,Q\
• If the
fault
is
induced
by a
rotation
of
faults
blocks,
then
the
fault
is a
spherical
surface.
In
such
a
case,
directions
of
curvatures
are
undetermined
and the
fault-throw
directions
cannot
be
deduced
from
the
analysis
of
these
curvatures.
When
the
fault-throw directions cannot
be
estimated,
it is
always possi-
ble for the
geologist
to
choose
interactively
a
small
set of
unit vectors
(t(ai),
1(0:2)5
• • •}
tangent
to the
fault
F
and to
substitute this
set to
J-(\,
9}
in
the filtering
procedure described above with
a
high value
for the
associated
certainty factors.
It is
important
to
note
that
fault-throw
directions
can
sometimes
be de-
duced
from
the
observation
of the
fault network.
For
example,
if a
fault
inter-
sects another
fault,
it is
wise
to
install
a
constraint
specifying
that,
along this
intersection,
the
fault-throw direction must
be
aligned with
the
intersection.
Computed
fault-throw
striae
For
each
fault
F,
the
fault-throw striae
can be
represented
as a
family
of
contour lines
of a
function
(p
defined
on
T.
To
achieve this,
<p
must
be
chosen
so
that
its
gradient remains tangential
to the
fault-throw direction t(x)
at
any
point
x of the
fault.
The
following
procedure
is
proposed:
•
Build
a
discrete
model
.A/1
1
(17,
JV,
(p,Cy)
associated
with
the
same
nodes
as
.M
3
(ft,JV,x,C
x
).
•
Build
an
initial
approximation
of
</?
in
such
a way
that
its
isovalues
are ap-
proximately
tangent
to the field of
fault-throw
direction
t(x)
at any
point
x
of
the
fault.
For
example,
one can
proceed
as
follows:
3
The
original source
of the
earthquakes
focal
mechanism
is the
Southern California
Earthquake Center:
//www.scecdc.scec.org/
.
375
376
CHAPTER
8.
ELEMENTS
OF
STRUCTURAL
GEOLOGY
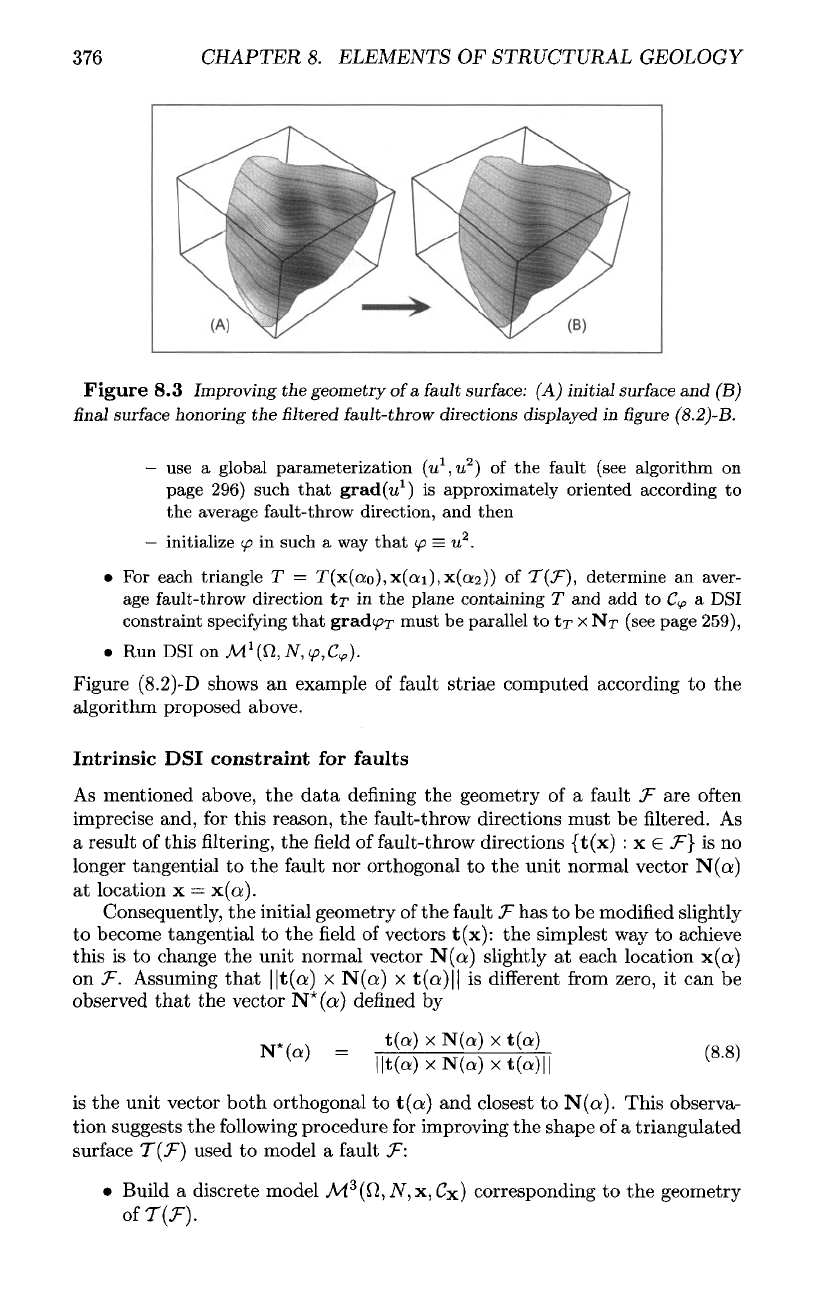
Figure
8.3
Improving
the
geometry
of a
fau7t
surface:
(A)
initial
surface
and (B)
final
surface
honoring
the filtered
fault-throw
directions
displayed
in figure
(8.2)-B.
—
use a
global
parameterization
(u
l
,u
2
)
of the
fault (see
algorithm
on
page
296)
such
that
grad(w
1
)
is
approximately
oriented
according
to
the
average
fault-throw
direction,
and
then
—
initialize
<p
in
such
a way
that
(p
=
u
2
.
• For
each
triangle
T =
T(x(ao),x(a:i),x(a2))
of
T(F),
determine
an
aver-
age
fault-throw
direction
tr
in the
plane
containing
T and add to dp a
DSI
constraint
specifying
that
grader
must
be
parallel
to
IT
x NT
(see
page
259),
• Run DSI on
M
l
(£2,
N,
(p,
C
v
).
Figure
(8.2)-D
shows
an
example
of
fault
striae
computed according
to the
algorithm proposed above.
Intrinsic
DSI
constraint
for
faults
As
mentioned above,
the
data
defining
the
geometry
of a
fault
T are
often
imprecise
and,
for
this reason,
the
fault-throw directions must
be
filtered.
As
a
result
of
this
filtering, the field of
fault-throw directions
(t(x)
: x €
F}
is no
longer
tangential
to the
fault
nor
orthogonal
to the
unit normal vector
N(o;)
at
location
x
=
x(a).
Consequently,
the
initial geometry
of the
fault
T has to be
modified
slightly
to
become tangential
to the field of
vectors t(x):
the
simplest
way to
achieve
this
is to
change
the
unit normal vector
N(a?)
slightly
at
each location
x(a)
on
F.
Assuming
that
||t(a)
x
N(o;)
x
t(a)||
is
different
from
zero,
it can be
observed
that
the
vector
N*(a)
defined
by
is
the
unit vector both orthogonal
to
t(a)
and
closest
to
N(o;).
This observa-
tion suggests
the
following
procedure
for
improving
the
shape
of a
triangulated
surface
T(F]
used
to
model
a
fault
F:
•
Build
a
discrete model
A4
3
(r2,
TV,
x,
C
x
)
corresponding
to the
geometry
ofT(.F).

8.1.
GEOMETRY
OF
FAULTS
AND
HORIZONS
• For
each node
a € fi,
compute
the
vector
N*(a)
defined
by
(8.8)
and
then
—
add a
fuzzy
Control-Normal-Vector
DSI
constraint
c'(a)
to
Cx
specifying
that
T(J-}
must
be
orthogonal
to
N*(a)
at
location
x(a)
(see page
265);
—
add a
fuzzy
Control-Straightline
DSI
constraint
c"(oi)
to
Cx
specifying
that
a can
move
only
on the
straight
line
passing
by the
point
x(a)
and
parallel
to the
direction
N*(a)
(see
page
264).
•
RunDSIonM
3
(ft,7V,x,Cx).
Figure (8.3) shows
an
example
of how filtered
fault-throw directions
can be
used
for
improving
the
geometry
of a
fault
surface
T(^):
after
applying
the
above algorithm,
the
normal vectors
to
T(F)
tend
to
become consistent with
the
computed
fault
striae.
It
should
be
noted
that
a
technique
to
align
the
minimum absolute normal
curvature directions with
specified
directions
will
be
presented
in the
next
sec-
tion.
If
need
be,
this technique
can be
combined with
the
procedure proposed
above.
8.1.2
Modeling horizons
In
sedimentary geology,
at the
time
of
deposition, horizons
are
assumed
to be
approximately horizontal
and are
thus approximately developable (see
defi-
nition
on
page 221).
Due to
tectonic events occurring throughout geological
time,
such horizons
are
deformed,
and
their shapes,
as
they
can be
observed
today, appear
as
folded
and
faulted versions
of
their initial horizontal devel-
opable shapes.
If
plastic deformations occurred during
the
tectonic events,
the
resulting
surface
for a
given horizon
<S
is no
longer "strictly" developable.
However,
in
practice,
folded
horizons remain
approximately
developable
and
their direction
of
minimum curvature
is
coincident with their (curvilinear)
axis.
For
example,
if we
consider
the two
surfaces represented
in figures
(8.4)-
A
and
(8.4)-B
respectively
and
having similar boundaries,
it can be
observed
that
the
saddle shaped surface
in figure
(8.4)-A
is far
from
being developable
while
the
anticline represented
in figure
(8.4)-B
can be
easily unfolded (devel-
oped)
on a
plane.
The
"basic"
DSI
harmonic weighting
coefficients
{v(a,fl}}
introduced
on
page
149 and
used
for
modeling most
of the
surfaces
of
this book
are
generally
quite
sufficient
for
interpolating
the
geometry
of
geological horizon. However,
as
shown
in
this section, when
the
(curvilinear) axis
of a
fold
is
known,
it is
possible
to use
anisotropic weighting
coefficients
{v(a,0}},
which take into
account such structural information.
Taking
into
account
the
axis
of a
fold
Consider
a
folded
horizon
<S
approximated
by a
triangulated surface
T(«S)
represented
by a
discrete model
,M
3
(0,
TV,
x,C
x
)-
Let us
assume
that
377
