Jean-Laurent Mallet. Geomodeling

338

CHAPTER

7.

CURVILINEAR TRIANGULATED SURFACES

• 6

boundary

Gregory

Control-Points

• 4

inner

Gregory

Control-Points

The

difficulty

arises

from

the two

pairs

of

Gregory

Control-Points

{po2'Po2}

and

{p

12

,

Pi2J5

which

are

shared with other edges

and

induce cross constraints

with

other adjacent triangles.

It can be

observed

in

figure

(7.12)

that

the

normal vector

N(w,

0) =

N(u,

0)

is

continuous through

the

common edge

-E^Po,

Pi)

if, and

only

if, the

common

axial tangent

x

u

(w,0)

and the

twin radial tangents

x

r

(w,

0) and

x

r

(w,

0) are

coplanar

for any

u

G

[0,1].

This coplanarity

is

ensured

if one can find

three

weighting

functions

a(w),

b(u),

and

c(u)

such

that

There

are

many possible choices

for the

unknown weighting

functions

a(it),

b(u),

and

c(u),

and

several

have been

studied

by Du and

Schmitt

(see [64,

65]).

For

simplicity's sake, linear

functions

have been chosen

as

follows:

This implies

that,

in

addition

to the

determination

of the 10

Gregory Control-

Points mentioned above,

the

continuity

of the

normal vector through

the

edge

E(p

0

,

p^

requires

the

determination

of the 4

additional

coefficients

60,

&i,

CQ,

and

ci

of

these linear weighting functions.

To

simplify

the

computations,

it is

wise

to

replace

(1

—

u}

by

w

in

b(u]

and

c(u)

and to

multiply a(u)

and

c(u)

by 1 = (u + w):

Using

these (unknown) linear weighting functions,

P(u]

becomes

a

polyno-

mial,

which

can be

developed

as

follows

on the

basis

of the five

monomials

{u

p

w

q

:p

+ q =

4}:

7.3.

GREGORY

Gl

PATCH

WORK

339

where

the

vectors

{Gi,...,

GS}

are

defined

as

follows:

The

polynomial

P(u)

defined

by

equation (7.8)

is

equal

to

zero

for any u G

[0,1]

if, and

only

if,

each

of its

coefficients

{Gi,...,

G

5

}

is

equal

to the

null

vector:

These

5

linear

vectorial

equations were initially proposed

by Du and

Schmitt

[64,

65] for

determining

the

unknown

10

Gregory Control-Points

and the 4

weighting

coefficients

corresponding

to the

solution

of our

problem.

7.3.2

A

solution based

on

DSI

This

section proposes

a

solution

based

on the DSI

algorithm.

The

resulting

method

is

slightly

different

from

the one

proposed

by Du and

Schmitt

arid

has the

following

advantages:

•

Knowing

an

approximation

of the

normal vectors

at the

vertices

of the

triangles

is not

required. Rather than building

the

Gregory Control-

Net

to

honor these constraints,

the

complete reverse

of

this strategy

is

proposed:

1.

compute,

with

DSI,

a first

approximation

of the

Gregory

Control-Net,

and

2.

deduce

the

normal

vectors

at the

vertices

from

this

first

approximation.

• All the

"micro edges"

of the

Gregory Control-Net

tend

to be of the

same length

(at

least locally)

and to be

distributed regularly around

the

Gregory Control-Nodes.

As a

side

effect,

this tends

to

stabilize

the

system

of

constraints (7.9)

and

avoids having

to

consider special cases

corresponding

to

pathological situations where

{62,63,04}

could

be

not

linearly independent.

340

CHAPTER

7.

CURVILINEAR

TRIANGULATED

SURFACES

•

Additional

DSI

constraints

can be

accounted for.

As

examples,

the

patchwork

can be

constrained

to

—

honor

data

points,

and

—

have approximately continuous curvatures

at the

vertices

of the

trian-

gular

patches.

In

practice,

the

proposed method

is

split into

four

steps:

Step

1:

Initializations

The first

step consists

of the

following

series

of

initializations:

•

Determine

the

location

of the

Gregory

Control-Points

{Pij}

on the

boundary

of the

patchwork.

Any

method

is

acceptable

to

accomplish

this;

however,

if the

patchwork

S to be

modeled

has to be

sewn

to an-

other

patchwork

<5*

along

a

common boundary

B(tS,<5*),

then

the

Gre-

gory

Control-Points

{p^-,p

fc

}

along

B(S,

«S*)

must

be

identical. Placing

such

a

condition

on the

Gregory Control-Points

of

B(S,S*}

guarantees

that

the two

resulting

surfaces

will

join smoothly without

any gap

along

the

sewing

curve corresponding

to

B(S,S*).

•

Create

a 2D

global

network

5

similar

to the one

shown

in

figure

(7.11)

and

linking

the

vertices

of all the

triangles

and

their associated Gregory

Control-Points.

•

Build

a

discrete model

.M

3

(Q,-/V,p,C

v

)

with

the

following

characteris-

tics:

—

Q

consists

of the set of all the

vertices

and the

Gregory

Control-Points

for

all the

triangles

of the

patchwork.

—

N(a)

is the set of

nodes

directly

linked

to a G fi in the

global

network.

—

<^(a)

is a

vector having three components

^(a),

(p

y

(a),

and

<p

z

(a)

for

any

a.

e

fl:

Ctp

is the set of DSI

constraints

that

is

initialized

to

contain

the

following

DSI

Control-Nodes:

*

All the

nodes corresponding

to

vertices

PJ

of the

triangles

are fixed

as DSI

Control-Nodes.

*

All the

Gregory Control-Points

{p^}

located

on the

boundaries

of

the

patchwork

are fixed as DSI

Control-Nodes.

5

Note

that

many

different

2D

global

networks

can be

created

from

the

initial

set of

vertices

and

Gregory

Control-Points.

However,

experimental

tests [197]

have

shown

that

the

network

shown

in figure

(7.11)

gives

the

best

results.

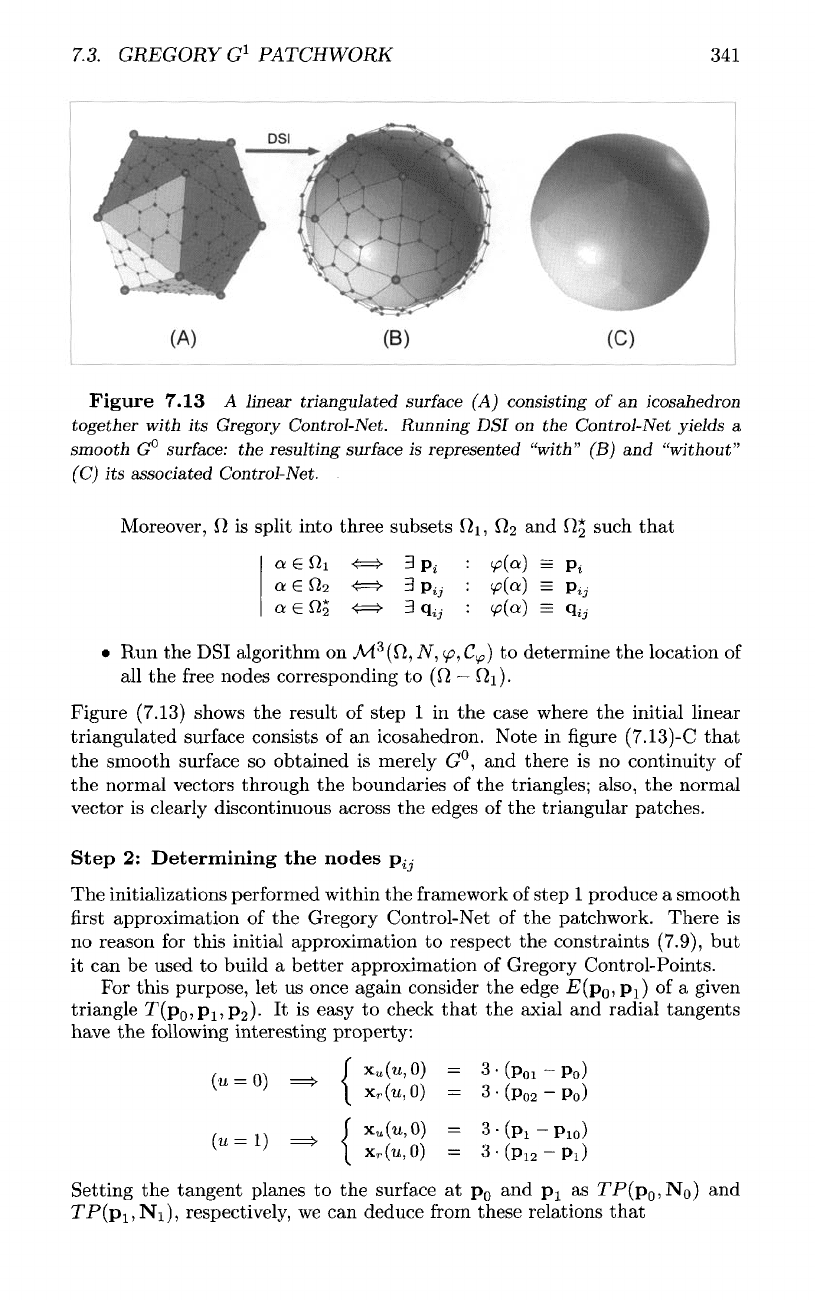
7.3.

GREGORY

G

l

PATCHWORK

341

Figure

7.13

A

linear

triangulated

surface

(A)

consisting

of an

icosahedron

together

with

its

Gregory

Control-Net.

Running

DSI

on the

Control-Net

yields

a

smooth

G°

surface:

the

resulting

surface

is

represented

"with"

(B) and

"without"

(C)

its

associated

Control-Net.

Moreover,

0 is

split into three subsets

fii,

£}

2

and

O^

such

that

• Run the DSI

algorithm

on

.M

3

(fi,

TV,

</?,

C^}

to

determine

the

location

of

all the

free

nodes corresponding

to

(17

—

f^i).

Figure (7.13) shows

the

result

of

step

1 in the

case where

the

initial linear

triangulated

surface

consists

of an

icosahedron. Note

in

figure

(7.13)-C

that

the

smooth surface

so

obtained

is

merely

G°,

and

there

is no

continuity

of

the

normal vectors through

the

boundaries

of the

triangles; also,

the

normal

vector

is

clearly discontinuous across

the

edges

of the

triangular patches.

Step

2:

Determining

the

nodes

p^

The

initializations performed within

the

framework

of

step

1

produce

a

smooth

first

approximation

of the

Gregory Control-Net

of the

patchwork. There

is

no

reason

for

this

initial approximation

to

respect

the

constraints

(7.9),

but

it

can be

used

to

build

a

better approximation

of

Gregory Control-Points.

For

this

purpose,

let us

once again consider

the

edge

E(p

Q

,

Pi)

of a

given

triangle

T(p

0

,p

1

,p

2

).

It is

easy

to

check

that

the

axial

and

radial tangents

have

the

following

interesting

property:

Setting

the

tangent planes

to the

surface

at

p

0

and

p

1

as

TP(p

0

,No)

and

TP(p

l5

Ni),

respectively,

we can

deduce

from

these relations

that

342

CHAPTER

7.

CURVILINEAR

TRIANGULATED SURFACES

Figure

7.14 Step

2 of the

construction

of a

Gregory

patchwork

yields

a

smooth

G°

surface

that

is

G

l

at the

vertices

of

the

triangles:

the

resulting

surface

is

repre-

sented

"with"

(A) and

"without"

(B) its

associated

Control-Net.

must

be

located

on the

plane

TP(p

0

,

NO)

must

be

located

on the

plane

TP(p

1

,Ni)

For

these

constraints

to be

respected,

it is

proposed

to

proceed

as

follows:

• For any

node

a\

G fii:

—

determine

the

unit

normal

vector

N(ai)

of the

average

plane

of its ad-

jacent

nodes

{(3i

£

7V(o:i)},

and

—

for

each

node

0i

e

N(a\),

add a

DSI

constraint

to

C(f>

specifying

that

<p(/3i)

must

lie in the

plane

TP(ip(cti),

N(ai)).

• Run the DSI

algorithm

on

.M

3

(Q,

TV,

</?,

C^}

to

determine

the

location

of

all the

free

nodes belonging

to

(Q

—

i7i),

while taking into account

the

newly

inserted constraints.

Due to the

fact

that

the DSI

constraints

are

honored

only

in a

least square sense,

for any

node

OL\

G

£li,

it

should

be

noted

that

the

updated locations

of the

nodes

{(3\

E

N(a\}}

do not

necessarily

respect

the

constraints

perfectly:

V?(/3i)

must

be

located

in the

plane

TP(<^(o:i),N(ai))

To

avoid possible small errors,

it is

proposed

to

project each

of

these

nodes

(p(fl\)

onto their associated plane

TP(<£>(ai),N(ai)).

• The set of

nodes

a%

G 0 are now at

their

definitive

location

and can be

added

as DSI

Control-Nodes

in the

list

C

v

so

that

the

current

set of

free

nodes

becomes

0^-

Figure (7.14) shows

the

intermediate result arising

from

step

2

described

above:

the

resulting surface

is

clearly

G

1

continuous

at the

vertices,

but is

still

G°

continuous along

the

common edges shared

by

adjacent triangles.

Poi

\

P02

J

Pio

\

Pl2 J

7.3.

GREGORY

Gl

PATCHWORK

343

Step

3:

Determining

the

coefficients

bi and

Q

So

far,

the

constraints (7.9)

specifying

that

G^

=

0

have

not

been taken into

account,

so

this

is the

goal

of

steps

3 and 4. Let us

consider

an

edge

E(p

0

,

p

1

)

shared

by two

triangles

T(p

0

,p

1

,p

2

)

and

T(p

0

,p

1

,p

2

),

and let

N

0

and

NI

be

the

unit normal vectors computed

at

step

2 at

nodes

a®

e

fii and

a\

e

QI

corresponding

to

p

0

and

p^

If

harmonic weightings

for the

{v(a,(3}}

are

used

in the

DSI

algorithm,

then

that

algorithm will tend

to

spread

the

points

p^

around each vertex

p^

uniformly,

implying

that

Moreover,

according

to

step

2, the

unit vectors

NO and

NI

have been built

in

such

a way

that

and

this implies that

It can be

deduced

from

these relations

that

the

constraints

GI

= 0 and

GS

=

0

attached

to the

edge

E(p

0

,p

l

')

will

be

honored

if

bo,

bi,

CQ,

and

c\

are

chosen

as

follows:

6

Due

to the

fact

that

DSI

tends

to

distribute

the

node

p^-

regularly around

the

vertices

p^

of the

triangles,

it can be

observed that

60 and

b\

are,

in

general,

such

that

These

coefficients

depend

on the

edge

E(p

0

,

p

x

),

which leads

to the

following

implementation

of

step

3 of the

proposed algorithm:

6

For

example,

the

value

bo is

obtained

in

this

way:

k

344

CHAPTER

7.

CURVILINEAR TRIANGULATED SURFACES

• For each edge E(p

0

,p

1

):

determine the two nodes a? E Q\ and a\ G fii corresponding to p

0

and

p

l5

respectively,

and

-

compute

the

coefficients

bo

(a?,

ai),

&i(a?,ai),

co(ai,ai),

andci(a?,ai).

Step

4:

Determining

the

nodes

q^

First,

observe

that

the

three

following

vectors

Xi,

X

2

,

and

X

3

depend solely

on

nodes

and

coefficients

(6

J5

c^)

that

have been determined

and fixed

during

the

previous steps

of the

proposed algorithm:

By

the end of

step

3

above,

the

constraints

GI

=

0 and

65

= 0 are

perfectly

honored,

leaving

the

following

three last constraints

to be

accounted for:

This

system

of

three vectorial equations

can be

turned into

a

matrix equation

(^234)

to

isolate

the

three

last

unknown vectors

of our

problem:

As

has

already been pointed out,

the

coefficients

60 and 61 are

generally

different

and the

rank

of the

3x4

matrix above

is 3. If one of the

vectors

to be

determined, say,

q

01

,

is

already known, then equation

((^234)

can be

rewritten

as

follows:

Assuming

that,

in

actual

fact,

60

7^

&i>

the

3x3

matrix above

can be

inverted

to

obtain

the

following

(Q^)

equation

which

then

allows

the

remaining vec-

tors

q

01

,

q

10

,

and

q

01

to be

determined:

7.3.

GREGORY

G

l

PATCHWORK

345

Figure

7.15

Final

result

for the

Gregory

patchwork

"with"

(A) and

"without"

(B)

the

associated

Control-Net

after

applying

step

4. The

resulting

surface

is now

G

1

everywhere.

This suggests

the

following

step

4 for the

algorithm

to

determine

the

location

of

the

nodes

a G

f^

that

correspond

to the

last Gregory Control-Points

q

01

,

q

01

,

q

10

,

and

q

01

to be

determined:

• For any

node

a G

f^,

install

a

DSI

constraint induced

by

equation

(^234)-

• Run the DSI

algorithm. This yields

a

smooth approximation

of the

location

of the

nodes

a €

O^.

However,

due to the

fact

that

equation

(^234)

can be

taken into account only

in a

least square sense

by the DSI

algorithm,

it is

necessary

to

apply

the

following

correcting phase:

• For

each edge

E(p

Q

^p

1

):

—

determine

the

four

nodes corresponding

to

q

01

,

q

01

,

q

10

,

and

q

01

,

re-

spectively,

and

—

update

the

location

of

q

01

,

q

10

,

and

q

10

according

to

equation

(G^)-

figure

(7.15)

shows

the final

result obtained

after

step

4

described above: this

result

is

clearly

a

G

1

smooth

surface.

7.3.3

DSI

constraints

This

section presents

the

implementation details

as to the DSI

constraints

used

at

steps

2 and 4 of the

algorithm proposed above:

Step

2:

Turning

<p(ay)

e

TP(p,N)

into

a DSI

constraint

As

shown

in

figure

(7.12),

consider

a

node

^(c^j)

=

p^

located

on an

edge

£'(p

0

,p

1

),

and let p be the

vertex,

p

0

or

p

l5

directly linked

to

</?(Q^).

This

346

CHAPTER

7.

CURVILINEAR

TRIANGULATED

SURFACES

vertex

p and its

associated

normal vector

N

define

a

pseudo-tangent plane

TP(p,N)

on

which

<p(otij)

must

be

located:

y>(a.ij}

located

on

TP(p,N)

This condition

is

equivalent

to the

following

linear equation:

This condition

can be

turned into

a

DSI

(cross) constraint

c =

c(o!ij),

as

denned

by

Define

9

c

((p,aij)

as

follows:

When

added

to the set of

constraints

C^

of the

discrete model

A

/

f

3

(0,

N,

(p,

C^),

the

above

DSI

constraint induces terms

7c

(

a

ij)

and

r^(a^)

in the DSI

equa-

tion such

that

Step

4:

Turning

£234

into

DSI

constraints

Let

us

consider

the

constraint

£234

=

G234(po,Pi)

attached

to the

edge

E(p

0

,p

1

)

of the

Gregory network

and let

^(p

0)

Pi)

be the

associated sub-

set of

fJ

defined

as

follows

(see

figure

(7.12)):

Using

these notations,

the

matrix equation

C?234(po,Pi),

as

defined

by

equa-

tions

(7.10),

becomes

a

system

of

constraints

to be

respected

by

(p:

7.3.

GREGORY

G

1

PATCHWORK

347

Noting

the

components

of the 3D

vectors

(p(ot)

and

Xj

as

{(p

v

(a)

:

v £

(x,y,z)}

and

{XJ

: v 6

(x,y,z)},

respectively,

the

system (7.13)

can be

turned into three sets

of

DSI

constraints

{c^

c^^c^}

that depend

on the

edge

£(P

0

;Pl)

Let

us

define

0^((p)

as follows for all v

e

{x,

y,

z}:

0r(*0

=

l-v

l/

(ttoi)

+

6o-V

I

'(aoi)

-

X?

8%(<f>-)

=

l-^(dSi)

+

^i-^Ki)

+

l-^O^

+

oo-v^Ko)

-

X£

03^)

=

l.^(c^

0

)+6i-^Ko)

-

X£

When added

to the set of

constraints

C^

of the

discrete model

Ai

3

(O,

TV,

</?,

C^,),

the

above three sets

of DSI

constraints induce

the

following

aggregated terms

7c

(

Q

)

an

d

TC(Q;)

in the DSI

equation:

,

-*

v

J

^W

=

2

(a =

ctoi)

=^>

<

\

H(a)

=

{0r(¥>)+02(¥0

-

2-^(^0}

r

<(a)

=

(6

0

)

2

+

(6i)

2

(a

=

aS

1

)

=»

<^

r

-

(a)

=

6

0

.{^(^)

- fto-^aSi)}

I

+

61-{^M

-

61

-^Ki)}

Jean-Laurent Mallet. Geomodeling

Подождите немного. Документ загружается.