Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.


358
CHAPTER
7.
CURVILINEAR TRIANGULATED SURFACES
Evaluating
the flow
(j>(a\(p}:
The
case
where
u(a)
€
3D
When
a
e
dD,
according
to
equations
(7.29),
and
(7.30),
it can be
observed
that
where
DT~
=
DT(OL,
a~,
/3~)
and
DT
+
=
DT(OL,
a
+
,(3
+
')
are the two
triangles
sharing
the
node
a and
having their edges
E(a,
a")
and
E(a,
a
+
)
located
on
the
boundary
dD
(see
figure
(7.18)).
Taking
into
account
equations
(7.33),
and
(7.35),
it can be
deduced
that
This leads
to the
conclusion
that
the flux
0(a|</?)
can be
expressed
as
follows
where
the
"boundary correction"
coefficients
{B@(a)}
are
defined
as
follows:
Note
that
the
above
definition
of the
coefficients
w(a,0)
encompasses both
o
the
case where
u(a)
e
dD and the
case where
u(a)
€£).
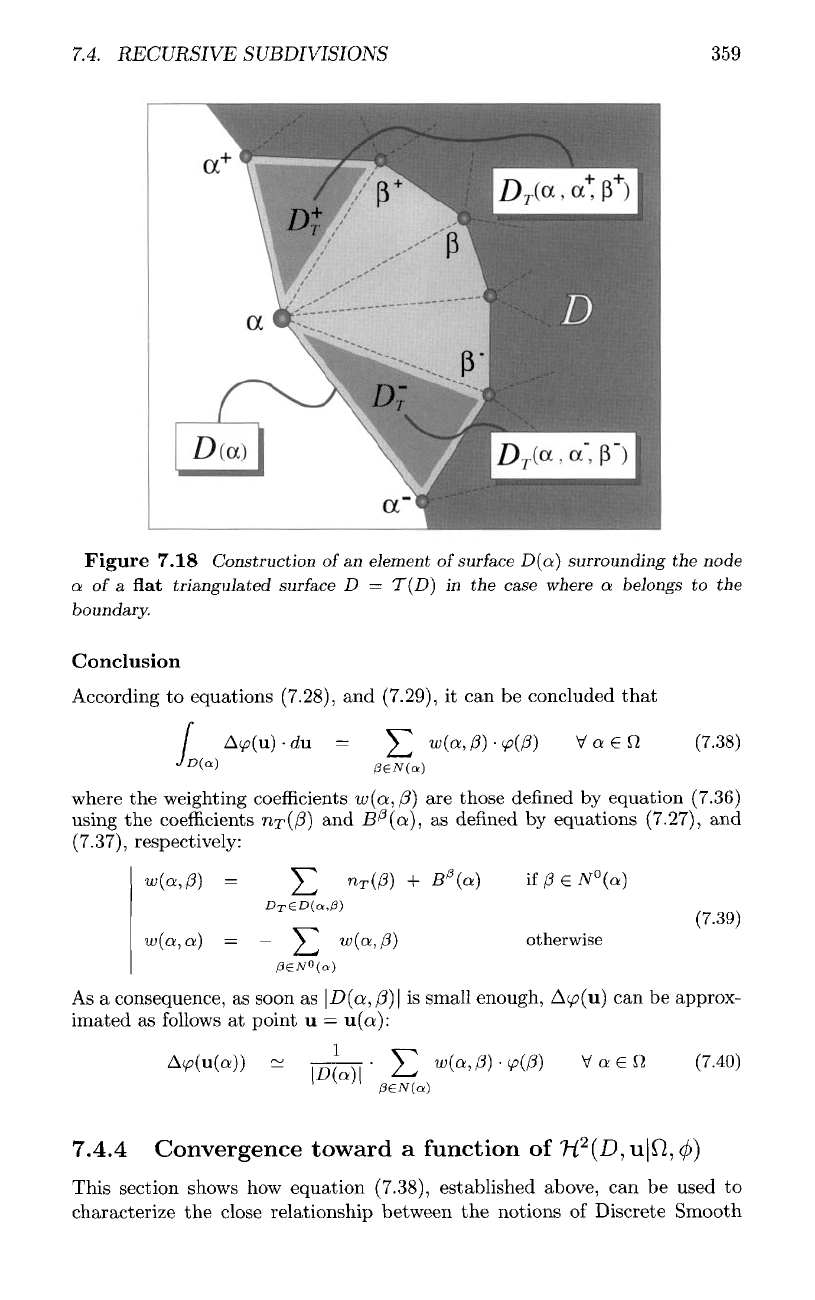
Figure
7.18
Construction
of
an
element
of
surface
D(o)
surrounding
the
node
a of a flat
triangulated
surface
D =
T(D)
in the
case
where
a
belongs
to the
boundary.
Conclusion
According
to
equations
(7.28),
and
(7.29),
it can be
concluded
that
where
the
weighting
coefficients
w(a,/3)
are
those
defined
by
equation (7.36)
using
the
coefficients
riT(f3}
and
B
f3
(a),
as
defined
by
equations
(7.27),
and
(7.37),
respectively:
As
a
consequence,
as
soon
as
D(a,
f3}\
is
small enough,
A</?(u)
can be
approx-
imated
as
follows
at
point
u
=
u(a):
7.4.4
Convergence toward
a
function
of
H
2
(D,u\£l,
0
This section shows
how
equation
(7.38),
established above,
can be
used
to
characterize
the
close relationship between
the
notions
of
Discrete
Smooth
7.4 RECURSIVE SUBDIVISIONS
359
4

360
CHAPTER
7.
CURVILINEAR
TRIANGULATED
SURFACES
Figure
7.19
Regular
recursive
subdivision
of
a
triangle.
Interpolation
and the
functions
of the
family
H
2
(D,
u|Q,
0).
Recursive
subdivision algorithm
Let
DT(OO,
CKI,
02) be a
triangle
of
T(D),
and let
OQ,
o^
and
o
2
be the
points
such
that
a'
0
—
midpoint
of the
edge
J5(o:i,
0:2)
a'i
=
midpoint
of the
edge
£'(0:2,0:0)
a
2
=
midpoint
of the
edge
E(ao,ai)
By
definition
and as
suggested
in figure
(7.19),
the
triangle
DT(OLQ,
0:1,0:2)
is
said
to be
regularly split
if it is
decomposed into
four
adjacent triangles
defined
as
follows:
Consider
now the
following
algorithm based
on a
recursive splitting
of the
triangles
of
T(D}:
//—
Recursive
subdivision
algorithm
•
T(D
[0]
)
<—
T(D]
• ft
[0]
=
set of
vertices
of
T(D]
• n
<—
0
while
(
more iterations
are
needed
) {
1)
T(D
[n+1]
)
<—
split regularly each
triangle
of
T(D
[n]
)
2)
Q
[n+1]
= set of
vertices
of
T(£>
[n+1]
)
3)
n
<—
(n + 1)
4)
set
<f
[n]
(a) =
<j>(a)
V a 6 ft
[0]
5)
fix all the
nodes
of ft
[0]
as
DSI
Control-Nodes
6)
apply
DSI to
p
[n]
}
II
end: while
At
each step
of
this recursive process,
the
existence
and
uniqueness
of the DSI
solution guarantees
that
each solution
(f>^
exists
and is
unique.
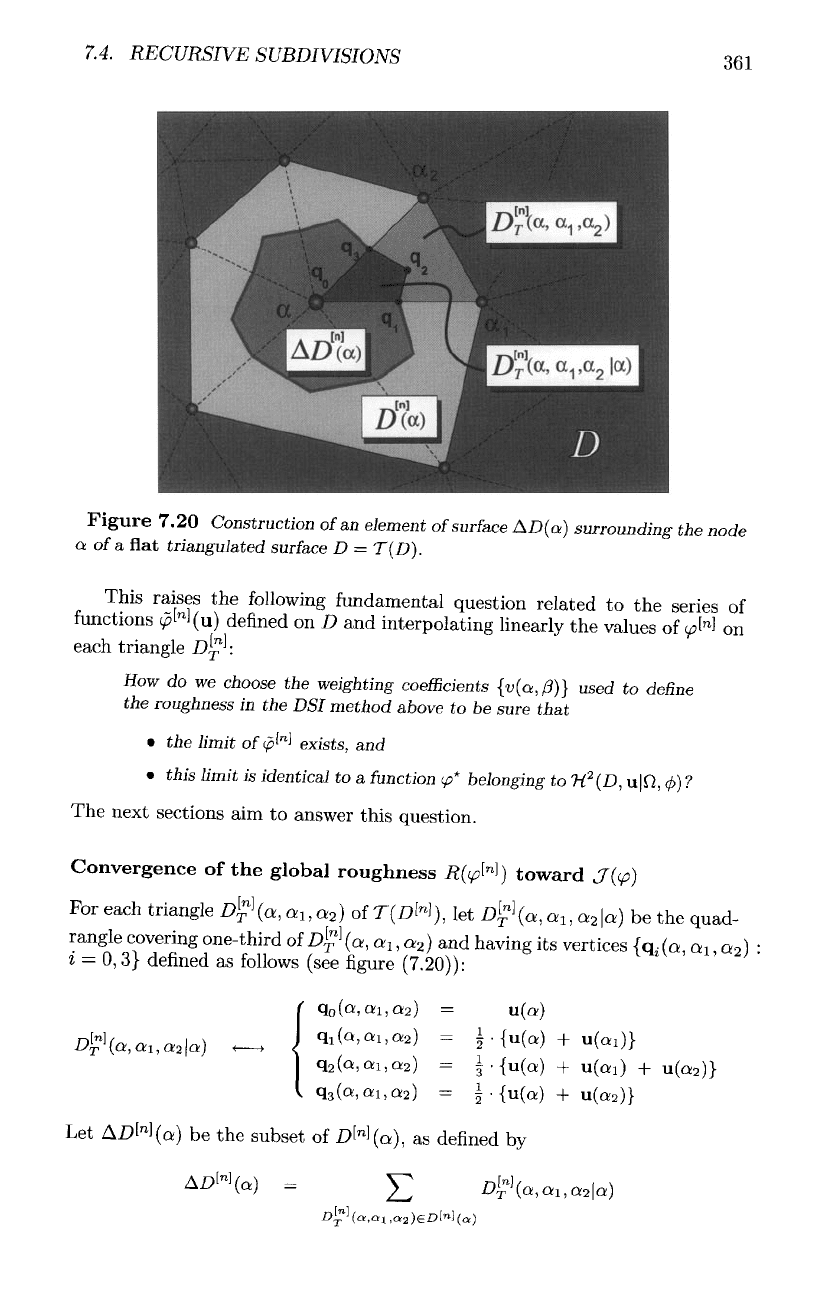
7.4.
RECURSIVE
SUBDIVISIONS
Figure
7.20
Construction
of
an
element
of
surface
A£>(a)
surrounding
the
node
a of a flat
triangulated
surface
D =
T(D).
This
raises
the
following
fundamental question related
to the
series
of
functions
<^
n
J(u)
defined
on D and
interpolating linearly
the
values
of
y?W
on
each triangle
D^:
How do we
choose
the
weighting
coefficients
{v(a,(3}}
used
to
define
the
roughness
in the
DSI
method
above
to be
sure
that
• the
limit
of
(p^
exists,
and
•
this
limit
is
identical
to a
function
<p*
belonging
to
H
2
(D,
u|fi,
0)
?
The
next sections
aim to
answer this question.
Convergence
of the
global roughness
R(<pW)
toward
J((p)
For
each
triangle
D
[
f
(a,
ttl
,
a
2
)
of
T(£>M),
l
et
D™
(a,
a
x
,
a
2
|a)
be the
quad-
rangle
covering one-third
of
D%
]
(a,
ai,a2) and having its vertices (q.a(a, QI «2) •
z
=
0,3}
defined
as
follows
(see
figure
(7.20)):
Let
AL>N(
a
)
be the
subset
of
D^(a),
as
defined
by
361

362
CHAPTER
7.
CURVILINEAR TRIANGULATED SURFACES
It can be
observed
that
As
a
consequence
and
according
to
equations
(7.38),
(7.39),
and
(7.40),
it can
be
seen
that
Ac/9(11(0:))
is
such
that
Similarly
and due to
equations
(7.41),
the
functional
J((p]
defined
by
equation
(7.17)
can be
obtained
as the
following
limit:
Consequently,
J(tp)
can
also
be
written
as
follows:
Let
us now
assume
that
the
DSI
method used
in the
recursive subdivision
algorithm presented above
is
based
on the
following
weightings:
The
associated local roughness
R((p^\a]
denned
by
equation (4.7)
is
According
to
equation (4.8),
the
global roughness
R((p^)
whose minimum
corresponds
to the DSI
solution
for
(f>^
is
defined
by
Assuming
that
the
stiffness
function
//(a)
used
in the
definition
of the
global
roughness
is
constant
and
equal
to
one-third
everywhere
on fi^l, and
tak-
ing
into account
the
conditions
(7.16)-2
and
(7.16)-3,
it can be
checked
that
R((?W)
is
such
that
Consequently, when
at the
limit, whether minimizing
J((p)
or
minimizing
the
global roughness
R((f>^}
is
equivalent.

7.4.
RECURSIVE SUBDIVISIONS
Convergence
of the
recursive
subdivision
algorithm
To
come back
to the
fundamental question
raised
on
page
361 and
related
to the
convergence
of the
series
(p^
generated
by the
recursive subdivision
algorithm,
let us
consider
the
function
(p\-
n
\u)
defined
on D and
interpolating
linearly
the
values
of
(p^
on
each triangle
D^
:
• Due to the
existence
and
uniqueness
of the
solution
of the
DSI
equation,
<p^
exists
and is
unique
for any
integer
n. The
formal proof
of the
convergence
of
the
series
of
functions
{<^'
n
'}
is
still
an
open problem.
It can be
observed
experimentally,
however,
that
</^
n
'
always
converges
toward
a
function
<p*
denned
on
D:
Practically
speaking,
it
seems
reasonable
to
conjecture
that
this
convergence
is
actually
true.
• If it is
assumed
that
the
limit
(7.45)
actually
exists,
then,
according
to
equa-
tion
(7.44),
it can be
deduced
that
(p*
belongs
to
H
2
(D,
u|fi,
</>):
As a
consequence,
if the
limit
(f>*
exists,
then
if*
is a C
2
function
10
interpo-
lating
the
values
(0(a)}
attached
to the set
f2
of the
vertices
of
T(D}.
Recursive
construction
of the
geometry
of a
C
2
surface
The
recursive subdivision algorithm based
on DSI
presented above
can
easily
be
used
to
build
a
smooth
C
2
surface
interpolating
the
vertices
of a
linear
triangulated
surface embedded,
for
example,
in 3D
space.
For
this
purpose
and
as
already mentioned,
at
each step
n of the
recursive process this algorithm
has
merely
to be
applied respectively
and
independently
to the
three components
x
x
(a),
x
y
(a),
andx^a)
of
the
vectors
{x(o:)
: a 6
£7^}
defining
the
geometry
of
the
surface
to be
modeled.
As
shown
in figure
(7.16),
this
discrete
approach
is
very
efficient
and can
reasonably compete with
the
parametric Gregory patchwork method pre-
sented
in
section (7.3)
and
illustrated
in figure
(7.1). Moreover,
it
should
be
noted
that
the
C
2
continuity
of a
parametric
surface
implies
its G
2
con-
tinuity.
As a
consequence,
at the
limit,
the
recursive subdivision algorithm
presented
above
tends
to
generate
a
G
2
surface.
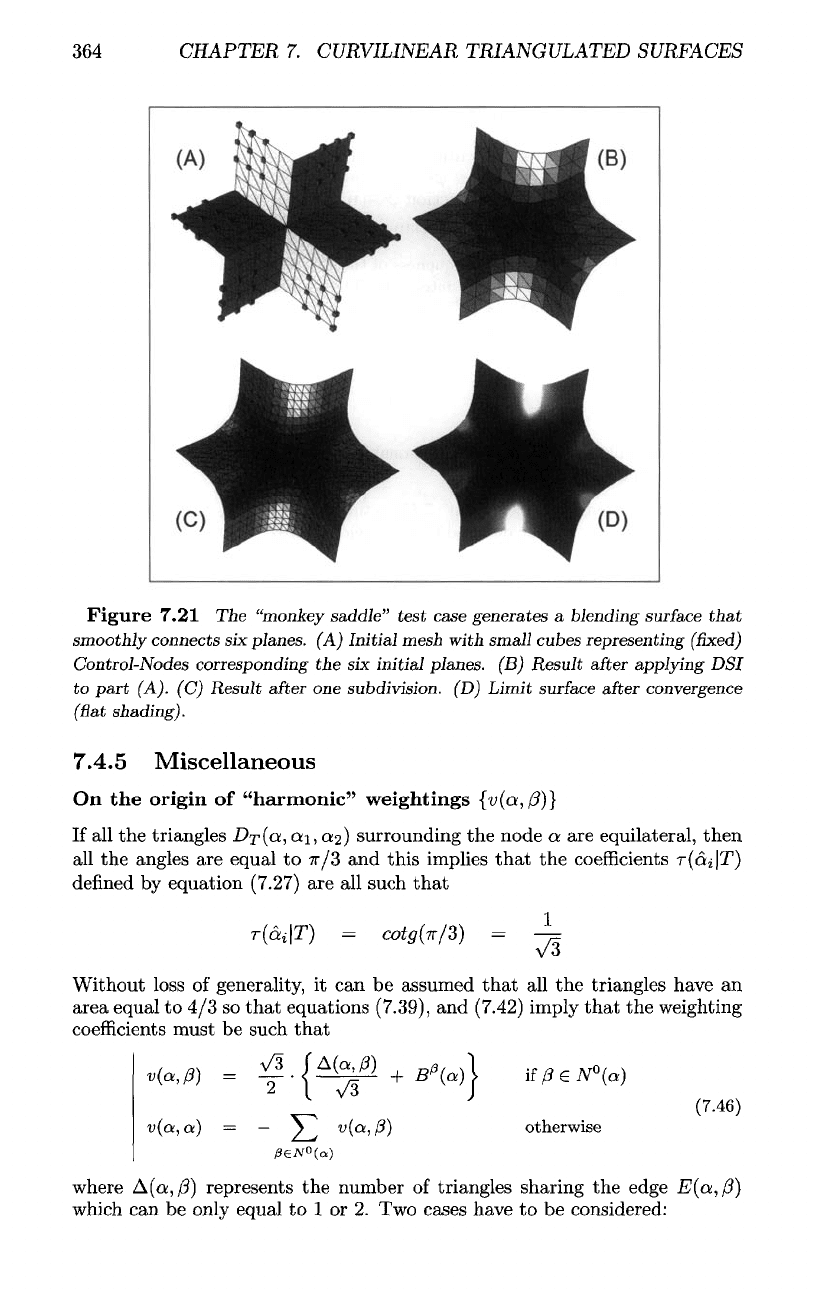
A
classic
test
for
subdivision algorithms consists
in
generating
a
"mon-
key
saddle"
surface
[229] corresponding
to a
blending
surface
that
smoothly
connects
six
planes radiating
in
different
directions.
As can be
seen
in figure
(7.21),
the
surface
generated using
the
above subdivision algorithm yields
an
excellent
result
with
no
undulations.
10
More precisely,
a
distribution (see
[194]).
363
364
CHAPTER
7.
CURVILINEAR
TRIANGULATED SURFACES
Figure
7.21
Tie
"monkey saddle"
test
case
generates
a
blending
surface
that
smoothly
connects
six
planes.
(A)
Initial
mesh
with
small cubes representing
(fixed)
Control-Nodes corresponding
the six
initial
planes.
(B)
Result
after
applying
DSI
to
part
(A).
(C)
Result
after
one
subdivision.
(D)
Limit
surface
after
convergence
(Gat
shading).
7.4.5
Miscellaneous
On
the
origin
of
"harmonic"
weightings
{v(a,(3}}
If
all the
triangles
DT(O.,
0:1,0:2)
surrounding
the
node
a are
equilateral, then
all the
angles
are
equal
to
Tr/3
and
this implies
that
the
coefficients
r(&i\T)
defined
by
equation
(7.27)
are all
such
that
Without loss
of
generality,
it can be
assumed
that
all the
triangles have
an
area equal
to 4/3 so
that
equations
(7.39),
and
(7.42)
imply
that
the
weighting
coefficients
must
be
such
that
where
A(a,/3)
represents
the
number
of
triangles sharing
the
edge
E(a,0)
which
can be
only equal
to 1 or 2. Two
cases have
to be
considered:
7.4.
RECURSIVE
SUBDIVISIONS
Figure
7.22 Examples
of
neighborhoods
N(a)
when
a is
located
on the
boundary
of
domain
D.
• If a is an
internal vertex, then
B
l3
(a),
is
equal
to
zero,
A(a,/3)
is
equal
to 2, and the
coefficients
{v(a,(3)}
are
identical
to the
harmonic weightings
introduced
on
page 149:
• If a
belongs
to the
boundary,
then
A(a,/3)
is
equal
to 1
while
B
l3
(a)
does
not
vanish.
In
this
case,
as
shown
in figure
(7.22),
the
actual value
of
v(a,/3)
depends
on the
number
of
a's
neighbors.
For
example:
—
in the
case
of figure
(7.22)-A:
—
in the
case
of figure
(7.22)-B:
365

366
CHAPTER
7.
CURVILINEAR TRIANGULATED SURFACES
—
in the
case
of figure
(7.22)-C:
—
in the
case
of figure
(7.22)-D:
In
the
case where
a
belongs
to the
boundary,
the
"boundary correction"
B@(a)
of the
coefficients
{v(a,fi)}
can
easily
be
understood.
In
this case,
a
is
not
located
at the
center
of
AD
(a).
Consequently,
it no
longer makes sense
to
minimize
the
discrepancy between
(p{ot)
and the
average value
of
(f>
on the
orbit
N°(a)
of
node
a:
most
of the
time,
the
weights
of the
neighboring nodes
not
located
on the
boundary vanish.
As a
consequence,
from
the
DSI
point
of
view,
any
point
a
belonging
to the
boundary
of the
surface
is
considered
more
as a
node
on a
curve
rather
than
a
node
on a
surface.
In
practice, using such
a
boundary correction makes
it
possible
to
avoid
some artifacts
that
could otherwise arise
on the
boundary
of
<S
when interpo-
lating
(p
with DSI.
Using
parameterization
for
controlling
anisotropy
The
parameterization
u =
(u
1
,
u
2
)
associated with
a
surface
is not
unique.
As
a
consequence,
one can
envision
denning
this parameterization
to
capture
a
priori information
related
to the
structure
of the
variations
of
(p.
In
particular,
if
(f>
is
known
to be
anisotropic along some curves drawn
on the
surface, then
it
is
wise
to
build
a
parameterization such
that
• one
of
the
parametric directions, let's
say
u
1
,
is
aligned
with
the
main direction
of
anisotropy
(see
page
297),
and
• the
gradients
of
u
1
and
u
2
are
chosen
to be
proportional
to the
magnitude
of
the
anisotropy
in
these
two
directions (see page
258).
Note
that
this approach enables curvilinear directions
of
anisotropy
to be
taken into account.
Exponential
map
weightings
{v(a,
(3)}
Most
of the
time,
one
would like
to
avoid
the
burden
of
building
a
param-
eterization
of the
surface
T(«S)
holding
the
property
</?
to be
modeled.
In
this case, assume
that
the
image
u(A<S(a))
of any
subset
A<5(o:)
of
S
sur-
rounding
a
node
a is
approximately
equal
to the
projection
of
AtS(o;)
on the
tangent plane
at
this location.
The
cotangent
of the
angles
9(a)
surrounding
each node
a can
then
be
evaluated
in
this tangent plane,
and the
weightings
{v(a,fl)}
can be
computed without
actually
building
a
parameterization
of
the
surface.
It
should
be
noted
that
such
an
approach
can be
used even
if the

7.4.
RECURSIVE SUBDIVISIONS
Figure
7.23
Evaluation
of the
DSI
weighting
coefficient
v(a,/3)
in the
case
where
a is an
internal
node:
v(a,0)
—
{cotg(0
+
(a,/3)
+
cotg(0~
(a,
/3)}/-\/\D(a)\.
surface
to be
modeled
is
closed: consequently,
the
recursive subdivision algo-
rithm presented above
for
open surfaces
can
also
be
applied
to the
modeling
of
smooth closed
surfaces.
For
the
sake
of
simplicity
and to
avoid some degenerated cases
that
can
arise when
the
tangent plane
is not
correctly estimated,
the
angles
9(a)
sur-
rounding
the
node
a on the
surface
T(S]
can
also
be
computed directly
in the
3D
space. However,
in the
case
of an
internal node
a,
generally these angles
do not add up to
27T,
and the
actual angles
9(a)
in the
parametric domain
have
to be
evaluated
as
follows,
where
{6^(a)}
represents
the set of all the
angles sharing
the
vertex
a in the 3D
embedding space:
More
generally,
0(a)
can be
evaluated
as
follows
where
/3(a)
is
assumed
to be
adjusted
to the
shape
of the
boundary
at
node
a
when
a is a
boundary node.
Assuming
that
all the
angles
9(ot)
surrounding
a
node
a are
equal,
it is
even
possible
to
simplify
the
determination
of
these angles:
in
this case,
it
suffices
to
assume
that
these angles
are
defined
by
367
