Jean-Laurent Mallet. Geomodeling

348

CHAPTER

7.

CURVILINEAR

TRIANGULATED SURFACES

Figure (7.1) gives

an

example

of a

triangulated

surface

smoothly interpolated

by

a

Gregory patchwork.

7.3.4

Additional

DSI

constraints

In

the

previous section,

a set of DSI

constraints

was

presented

that

must

be

used

for

defining

the

location

of the

nodes

of the

Gregory Control-Net

of

all

the

triangles

of the

triangulated

surface

to be

modeled.

In

addition

to

these mandatory constraints,

it is

possible

to

account

for

optional additional

constraints.

In

the

previous section,

a set of

mandatory

DSI

constraints

was

presented

for

denning

the

location

of the

Gregory Control-Net nodes

of all the

triangles

belonging

to the

triangulated

surface

to be

modeled.

In

addition

to

these

mandatory constraints,

it is

also possible

to

account

for

optional additional

constraints,

as is the

subsequent example.

Interpolating

a

data

point

Consider

a

triangle

T(p

0

,p

1

,p

2

)

belonging

to the

triangulated surface

to be

modeled.

This paragraph addresses

the

problem

of fitting the

associated Gre-

gory

patch

in

such

a way

that

it

interpolates

a

given

data

point

p.

To

simplify

the

presentation

of a

solution based

on

DSI,

for

each vertex

{p

i

: i =

0,1,2}

of the

triangle

T(p

0

,p

1

,p

2

),

a

subset

O

i

(p

0

,p

1

,p

2

)

com-

posed

of five

nodes

of

O

is

defined

as

follows

(see

figure

(7.12)):

Moreover,

for

simplicity's sake,

the

following

notations will

be

used:

• the

barycentric

coordinates

(w,w,

v)

relative

to the

vertices

p

0

,

p

x

,

and

p

2

of

T(p

0

,p

1;

p

2

)

a

re

renamed

(uo,Ui,U2):

• the

indices

of the

nodes

a G

Qj(p

0

,p

1

,p

2

)

and the

coordinates

Ui are

num-

bered

modulo

3:

7.3.

GREGORY

G

l

PATCHWORK

349

Using

these

symmetrical notations, equation

x(w,

v)

=

S(UQ,U

1,112)

of the

Gregory

patch

can be

written

as a

function

of

(f>:

Let c be an

index

function

of the

following

parameters

and let

{^4

c

(a)}

be the fifteen

associated

coefficients

defined

as

follows:

With these notations,

the

Gregory patch equation

can be

written

in a

very

concise

form:

Let

us now

consider

the

problem

of

constraining

the

Gregory patch

to

honor

the

given

data

point

p in

such

a way

that

where

(UQ,

wi,

1^2)

are

given

barycentric coordinates.

In

practice,

if the

linear

interpolation

of the

triangle

T

(p

0

,p

1

,p

2

)

is

close

to the

data

point

p,

then

the

barycentric coordinates

of the

projection

of p on the

plane corresponding

to

this linear interpolation

can be

chosen

for

(UQ,

11,1,112)

•

The

above constraint (7.14)

can be

turned into three independent

DSI

constraints associated with

the

index

c

such

that

350

CHAPTER

7.

CURVILINEAR TRIANGULATED SURFACES

Figure

7.16

An

example

of

smooth

triangulated

surface

obtained

by

applying

DSI

to a

recursive

subdivision

of the

initial

linear

triangulated

surface

represented

in figure

(6.1).

(A)

Initial

mesh,

(B)

result

after

one

subdivision,

(C)

result

after

two

subdivisions,

and (D)

limit

surface after

convergence

(fiat

shading).

Let us

define

0"((p]

as

follows:

When added

to the set of

constraints

C

v

of the

discrete model

A^

3

(O,

JV,

</?,

C

v

),

the

above

DSI

constraint

induces terms

7^

(CK)

and

r^(a)

in the DSI

equation

such

that

7.4

Recursive

subdivisions

Up

to

now, piecewise algebraic representations have been proposed

for

build-

ing

a

smooth triangulated

surface.

This section proposes

a

very

different

approach, where

a

smooth surface

is

obtained

as the

limit

of a

series

of

piece-

wise

linear

triangulated

surfaces generated

by

recursive subdivisions

of the

initial surface's triangles (see

figure

(7.16)).

7.4.1

Introduction

Consider

an

open

linear triangulated

surface

T(«S),

and let

Q

be the set of

its

vertices. According

to

section (6.5),

it is

always

possible

to find at

least

one

global

parameterization

u

=

(w

1

,

it

2

)

of

T(«S)

in

1R

defined

by its

values

7.4.

RECURSIVE SUBDIVISIONS

(u(a )

: a £

f2}

on

0,

and

each rectilinear

flat

triangle

T of

T(«S)

has an

image

noted

as DT in the

parametric space

IR

2

:

The

global parameterization

u is

assumed

to be

linearly interpolated

on

each

triangle

of

T(S]

from

its

values

at the

vertices, which guarantees

that

• for

each

triangle

T of

T(«S),

the

domain

DT is

itself

a

rectilinear

triangle

in

the

parametric

domain,

and

• the set D =

T(D}

as

defined

by

is

a flat

triangulated

surface

in the

parametric

domain

corresponding

to the

image

of

T(<S):

In

the

following

sections,

a new

method, designed

to

approximate

a C

2

para-

metric surface based

on

such

a

parameterization

and

interpolating

the

vertices

of

T(S),

is

proposed.

Family

H

2

(D,uO,0)

Let

</>

be a

given discrete

function

denned

by its

values

on

Q:

By

definition,

H

2

(D,

u|0,0)

denotes

the

family

of all the

functions

(p

defined

on

D and

such

that

7

where

J((f]

is the

functional

8

defined

as

follows:

Using

the

family

H

2

(-D,u|0,

0),

it is

straightforward

to

build

a

smooth

C

2

parametric

surface

interpolating

the

vertices

(x(o;)

: a

G

£7}

of

T(«S).

It

suffices

to

choose

the

components

x

(a),

x

y

(a),

and

x

z

(a)

of the

vector

x(u)

7

The

C

2

continuity

of

ip

is

assumed

to be

achieved

in the

distribution sense (see

[194]).

8

The

symbol

A</?(u)

represents

the

Laplacian

of

y(u),

as

defined

by

351

352

CHAPTER

7.

CURVILINEAR TRIANGULATED SURFACES

corresponding

to the

parametric representation

of the

surface

to be

modeled

as

follows:

It can be

checked

that

the C

2

continuity

of the

components

of

x(u) implies

the

G

2

continuity

of the

resulting surface.

The

following

discussion will show

that

the

interpolation

so

denned

can be

approximated

in a

discrete

way

thanks

to an

algorithm based

on

DSI

coupled

with

a

recursive subdivision

of the

initial triangles

of

T(S}.

Remark

It can

easily

be

shown

that

7i

2

(D,

u|fi,

0) is not

empty. Consider,

for

example,

the

family

of

functions

{</?[«]}

defined

as

follows

where

the

radial functions

{ip[

a

,n](

r

}}

are

assumed

to be

denned

by

If,

for

each

a

E

O,

R(a)

is a

positive parameter chosen

in

such

a way as to

o

represent

the

radius

of an

open

2-ball

BR(

a

)(u(a))

(see page

29)

centered

on

u(a)

and

fully

contained

in the

Voronoi region (see page

99) of

u(a),

then

</?[

n

],

as

defined

by

equation (7.18), belongs

to the

family

7i

2

(D,ufJ,0)

for

any

integer

n

>

1.

Moreover,

it

should

be

noted

that

each

function

(p^

so

denned

is

C

n+l

continuous.

7.4.2

Notations

T(D)

triangles

This

section

presents

some

notations

and

geometric

results

that

will

be

used

in

the

next section

for

computing

an

approximation

of

A(£>(u)

based

on a

linear

approximation

of

(p

on

each triangle

of

T(D}.

Notations

For

reasons

of

conciseness,

in the

rest

of

this chapter,

any

triangle

of

T(D)

having

u(a),

u(ai),

and

11(0:2)

for

vertices

is

noted

as

DT(&,

01,0:2)

or,

more

simply,

as

DT'-

Moreover,

the

following

notations

are

used:

•

|-Dr|

is the

area

of

DT(OL,

ai,

0:2).

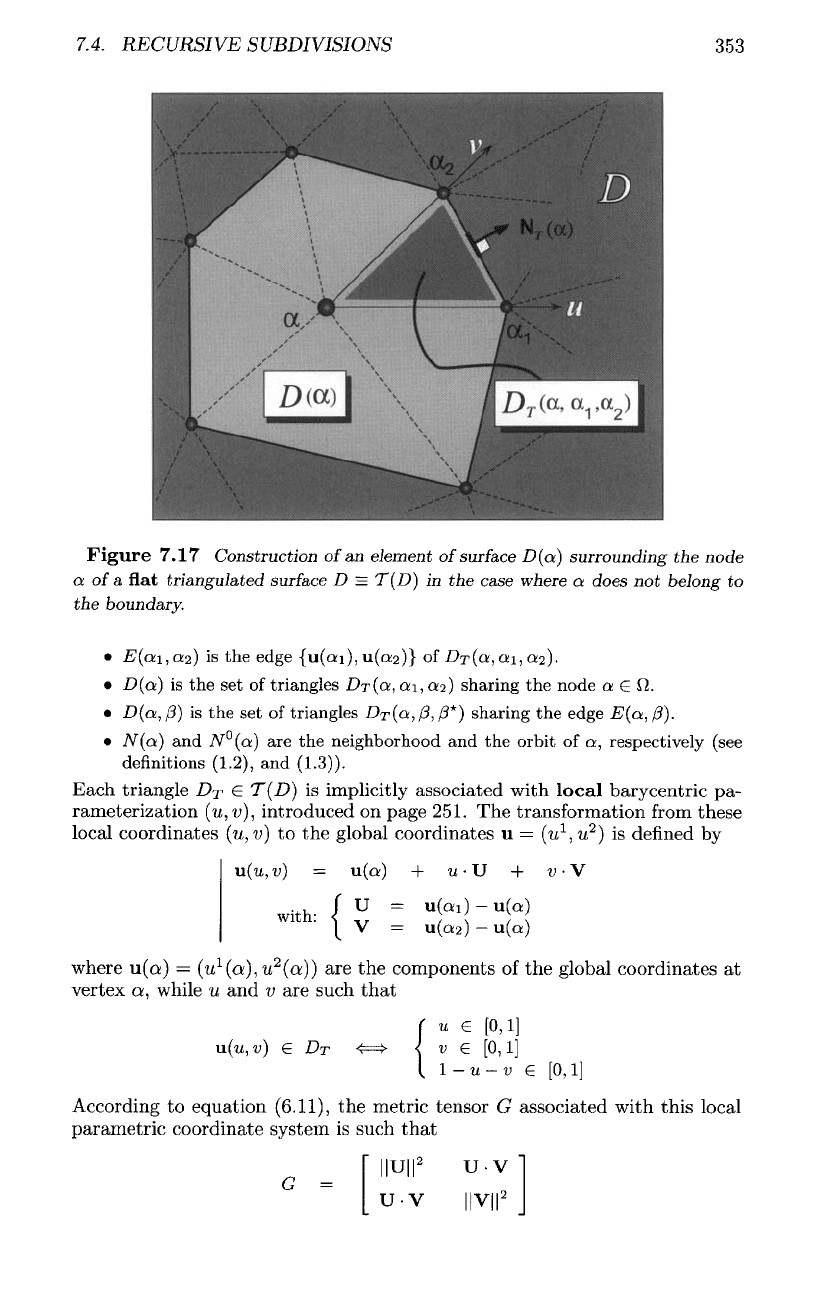
7.4.

RECURSIVE SUBDIVISIONS

Figur e

7.17

Construction

of

an

element

of

surface

D(oi)

surrounding

the

node

a

of

a flat

triangulated

surface

D

=

T(D)

in the

case

where

ct

does

not

belong

to

the

boundary.

•

£(0:1,0:2)

is the

edge

{u(ai),

11(0:2)}

of

DT(Q:,Q:I,

0:2)-

•

D(a]

is the set of

triangles

-Dr(o:,

01,

0:2)

sharing

the

node

a

e

f2.

•

D(a,0)

is the set of

triangles

DT(OC,

/3,/3*)

sharing

the

edge

E(a,0).

•

N(a)

and

N°(a)

are the

neighborhood

and the

orbit

of a,

respectively

(see

definitions

(1.2),

and

(1.3)).

Each triangle

DT

£

T(D]

is

implicitly associated with

local

barycentric

pa-

rameterization

(M,

v),

introduced

on

page 251.

The

transformation

from

these

local coordinates

(u,v)

to the

global coordinates

u —

(u

l

,u

2

)

is

denned

by

where

u(a)

=

(u

l

(a),

u

2

(a})

are the

components

of the

global coordinates

at

vertex

a,

while

u and v are

such

that

According

to

equation

(6.11),

the

metric tensor

G

associated with

this

local

parametric coordinate system

is

such

that

353

354

CHAPTER

7.

CURVILINEAR TRIANGULATED SURFACES

The

determinant

of G is

noted

as

g,

and it may be

observed

that

the

area

DT(&I

c*i,

c^)!

of the

triangle

DT((*,

cti,

0:2)

is

such

that

Unit

normal

vector

NT

(a)

The

height

h of the

triangle

DT(CK,

oti,

0:2)

from the

vertex

u(a)

onto

the

edge

£^(01,0:2)

is

such

that

As

shown

in figure

(7.17),

NT

(a)

represents

the

unit vector located

in the

plane

of

DT(OL,

a\,

0.2)

and

such

that

•

NT(CK)

is

orthogonal

to the

edge

E(a\,a.<2)

of

DT(G.,

0:1,

012),

and

•

NT(CK)

is

oriented outward relative

to

DT(&,

cti,

0:2)-

It

should

be

observed

that

/i

and

NT

(a) are

denned

by the

following

equa-

tions:

N

T

(a)

=

Nr(a)-U

+

Nr(a)-V

and h =

N

T

(a)

• U =

N

T

(a)-V

Multiplying

(scalar product)

the first

equation above

by U and

then

by V,

yields

the two

following

equations

where

N^(a)

and

N^(CK)

represent

the

(contravariant) components

of

NT

(a)

relative

to the

frame

(U, V). It can be

observed

that

and

this implies

that

equation

(7.20)

can be

solved:

Taking into account equation

(7.19),

it can be

concluded

that

the

(contravari-

ant) components

of

NT

(a)

relative

to the

frame

(U, V) are

such

that

7.4.

RECURSIVE SUBDIVISIONS

Let

W = (V

—

U) be the

vector corresponding

to the

edge

of

DT(a,

01, 02)

opposite

to the

vertex

a and let (a,

01,02)

be the

angles

of

Z>r(o,

01,02)

corresponding

to the

vertices

(0,0:1,0:2),

respectively.

It can be

observed

that

^

=

2

•

|D

T

(a,ai,a

2

)|

=

||U||

-

||W||

•

sin^)!

=

||V||

•

||W||

•

|sin(d

2

)|

(7.23)

Taking into account equations

(7.22),

and

(7.23)

makes

it

possible

to

write

equation

(7.21)

in the

following

form:

Observing

that

the

angles

01 and 02

always belong

to [0,

TT]

so

that

their sine

is

always positive,

it can be

concluded

that

Non-unit

normal

vector

nr(o)

For

each triangle

DT(OL,

01,

02)

of

T(D],

it is

useful

to

introduce

the

non-unit

vector

n

T

(a)

colinear

to

N^(o)

and

proportional

to the

length

of its

edge

£"(01,02):

Using

equation

(7.19),

it can be

deduced

that

the

(contravariant) components

(n^(o),

n^(o))

of

this vector relative

to the (U, V)

frame

attached

to T are

such

that

If

r(ai|T(o,

01,02))

represents

the

cotangent

in

parameter

space

of the

angle

o^

at

vertex

a.i

of the

triangle

T(o,

01, 02)

then

the

components

(n^o:),

n^(o)}

are

such

that

7.4.3 Approximating

Ay?(u)

on

D(a)

In

this section,

it is

proposed

to

approximate

A(^(u(o))

as the

average value

of

A(/?(u)

on

D(a):

355

356

CHAPTER

7.

CURVILINEAR TRIANGULATED SURFACES

For

this

purpose,

first

observe

that

According

to the

Green-Gauss

theorem

9

[14],

the flow

<j>(a\ip)

of

gradt/?

through

the

boundary

dD(a)

of

D(a)

verifies

the

following

equation

where

N is the

unit vector

of

JR

2

,

orthogonal

to

dD(ot)

and

oriented positively

outward relative

to

D(a).

It is

proposed

to

proceed

in two

steps

to

evaluate

this

integral:

• first,

evaluate

the flow

4>(a,

QI,

Q.-2\(p)

through

the

boundary

{dD(a)r\DT(a,

ai,

0:2)}

of

each

triangle

DT(OL,

ot\,

0:2)

of

-D(a),

and

•

next,

add up

these

flows

</>(«,

ai,

a^lv

7

)

for all the

triangles

of

D(a)

to

obtain

0(a|¥>)>

In

practice, depending

on the

position

of a

relative

to the

boundary

of

D(a),

two

cases need

to be

considered.

Definition

and

evaluation

of the flow

(f)(a,ai,a.2\(p)

Let

(f>(a,ai,a2\<p)

be the flow of

grad</?

exiting

Z>r(a:,ai,

0:2)

through

the

edge

E

(01,02)

as

defined

by the

following

equation where

N

T

(a)

is the

unit normal vector orthogonal

to

E(a\,

0.2)

oriented positively outward

from

D

T

(a,ai,a

2

):

It can be

observed

that,

due to the

linear variation

of

(p

on

DT(G.,

ot\,

0:2)

and

according

to

equation

(6.12),

the

gradient

grad</?

is

constant

on

DT(OL,

«i,

02}

and

is

such

that

Taking into account equations (5.17),

and

(7.24),

it can be

deduced

that

the

scalar product

of

grad<p

with

the

unit normal vector

NT

(a:)

is

such

that

9

Let S be a

piece

of

surface

bounded

by a

closed curve

dS

having

a

unit normal vector

N

oriented

outward

relative

to S. For any 2D field of

vectors

W, the 2D

version

of the

Green-Gauss theorem

states

that

the

following

relationship

is

true:

7.4.

RECURSIVE SUBDIVISIONS

According

to

equation

(7.30),

the flow

0(a,a.i,a.2\(p)

can

then

be

computed

thanks

to the

following

curvilinear integral

on the

edge

E(oti,a2)'.

From

equations

(7.25),

(7.31),

and

(7.32),

it can

easily

be

concluded

that

(f>(a,ai,a

2

<f>)

=

r(d

2

|T)-</?(ai)

+

r(di|T)-^(a

2

)

-

{r(di|T)

+

r(a

2

|T)}-^(a)

where

the

coefficients

{r(ai|T),

r(a-2\T}}

are

those

denned

by

equation

(7.27).

o

Evaluating

the flow

<f)(a\(p):

The

case

where

a

£D

o

When

a G

D,

according

to

equations

(7.29),

and

(7.30),

it can be

observed

that

Taking into account equations (7.33),

and

(7.34),

(j)(a\(p)

can be

written

as

which

makes

it

possible

to

conclude

that

357

Jean-Laurent Mallet. Geomodeling

Подождите немного. Документ загружается.