Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.


318
PTER
7.
CURVILINEAR
TRIANGULATED
SURFACES
Figure
7.1 An
example
of
Gregory patchwork smoothly interpolating
the
vertices
of
the
initial linear triangulated
surface
represented
in figure
(6.1).
This explains
why the
modeling
of
triangulated
surfaces
is
currently
one of
the
most active
fields
of
research
in
CAD.
Within
the
framework
of
this chapter, three
different
approaches
are
pro-
posed
for
building
a
smooth
surface
interpolating
the
vertices
of a
given
tri-
angulated
surface:
1.
The first
approach consists
in
approximating each triangle, individually, with
a
smooth parametric curvilinear patch.
2.
Approximating each triangle, individually, with
a
smooth curvilinear facet
may
generate discontinuities along
the
edges shared
by
pairs
of
triangles.
Thanks
to a
method based
on
DSI,
it
will
be
shown
that
the
parameters
of
each
individual curvilinear
facet
can be
determined
to
ensure
G
l
continuity
along
the
edges
of the
triangles.
3.
Finally,
it
will
also
be
shown
that
a
discrete approximation
of a G
2
surface
interpolating
the
vertices
of the
triangulated surface
can be
built. Such
an
approximation
is
obtained
by
recursive subdivisions
of the
initial
surface,
and
the
location
of the new
vertices
so
generated
are
computed thanks
to the DSI
method.
7.2
Building
a
smooth
curvilinear triangle
7.2.1
Preliminary
definitions
Unit parametric domain
DT of a
triangle
T
Let
(u,v)
be an
orthonormal coordinate system
of
M
2
.
By
definition,
"tri-
angle's unit parametric domain"
or,
more simply, "triangle's domain,"
is the
name
given
to the
subset
DT of
points
of M
whose coordinates
(u,
v)
are
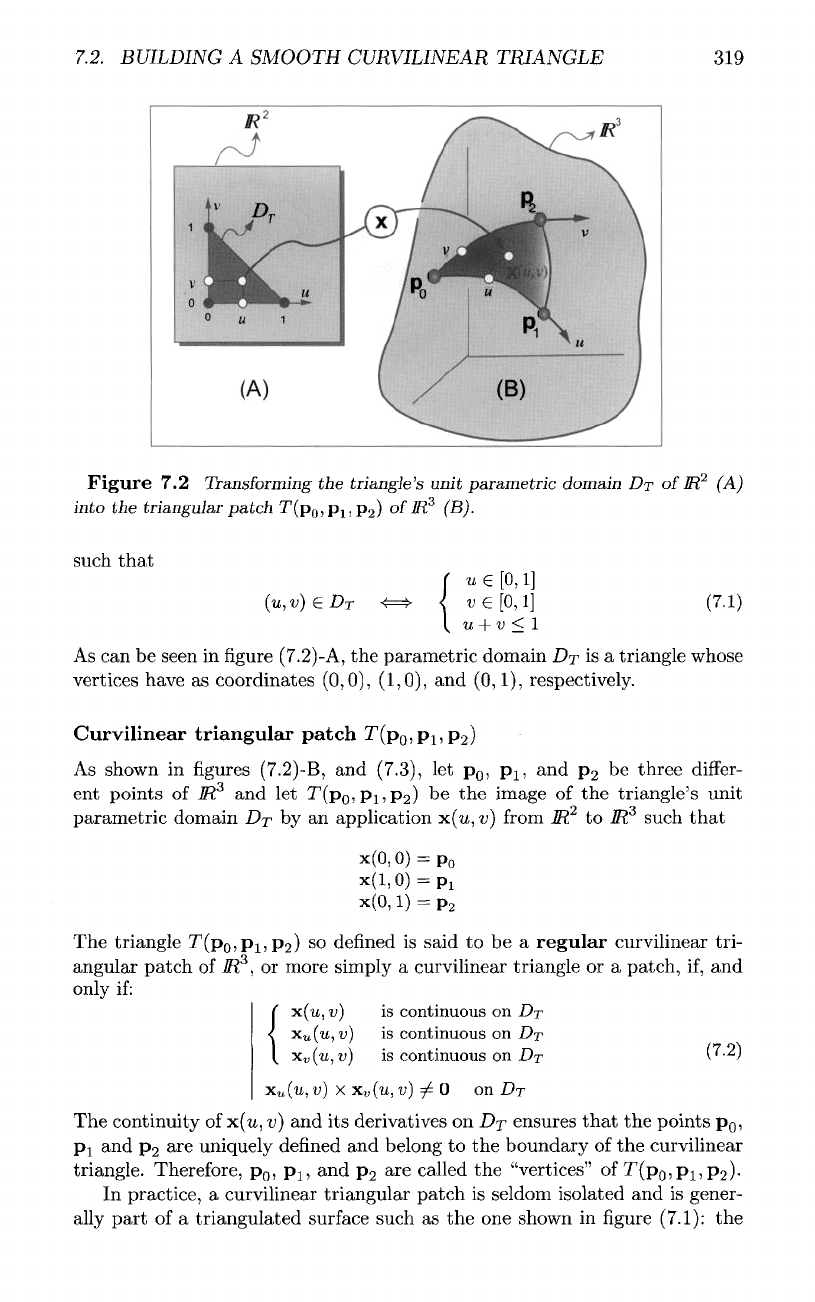
7.2.
BUILDING
A
SMOOTH CURVILINEAR TRIANGLE
319
Figur e
7.2
Transforming
the
triangle's
unit
parametric
domain
DT
of
1R
2
(A)
into
the
triangular
patch
T(p
0
,p
1
,p
2
)
of
M
3
(B).
such
that
As
can be
seen
in figure
(7.2)-A,
the
parametric domain
DT is a
triangle whose
vertices have
as
coordinates
(0,0),
(1,0),
and
(0,1),
respectively.
Curvilinear
triangular
patch
T(p
0
,p
1
,p
2
)
As
shown
in figures
(7.2)-B,
and
(7.3),
let
p
0
,
p
l5
and
p
2
be
three
differ-
ent
points
of
JR
3
and let
T(p
0
,p
1
,p
2
)
be the
image
of the
triangle's unit
parametric domain
DT by an
application
x(w,
v)
from
JR
to
1R
3
such
that
The
triangle
r(p
0
,p
1
,p
2
)
so
defined
is
said
to be a
regular
curvilinear
tri-
angular
patch
of
IR
3
,
or
more simply
a
curvilinear
triangle
or a
patch,
if, and
only
if:
The
continuity
of
x(w,
v)
and its
derivatives
on DT
ensures
that
the
points
p
0
,
Pi
and
p
2
are
uniquely
defined
and
belong
to the
boundary
of the
curvilinear
triangle. Therefore,
p
0
,
p
1?
and
p
2
are
called
the
"vertices"
of
T(p
0
,p
1
,p
2
).
In
practice,
a
curvilinear triangular patch
is
seldom isolated
and is
gener-
ally
part
of a
triangulated surface such
as the one
shown
in figure
(7.1):
the
319
320
CHAPTER
7.
CURVILINEAR TRIANGULATED SURFACES
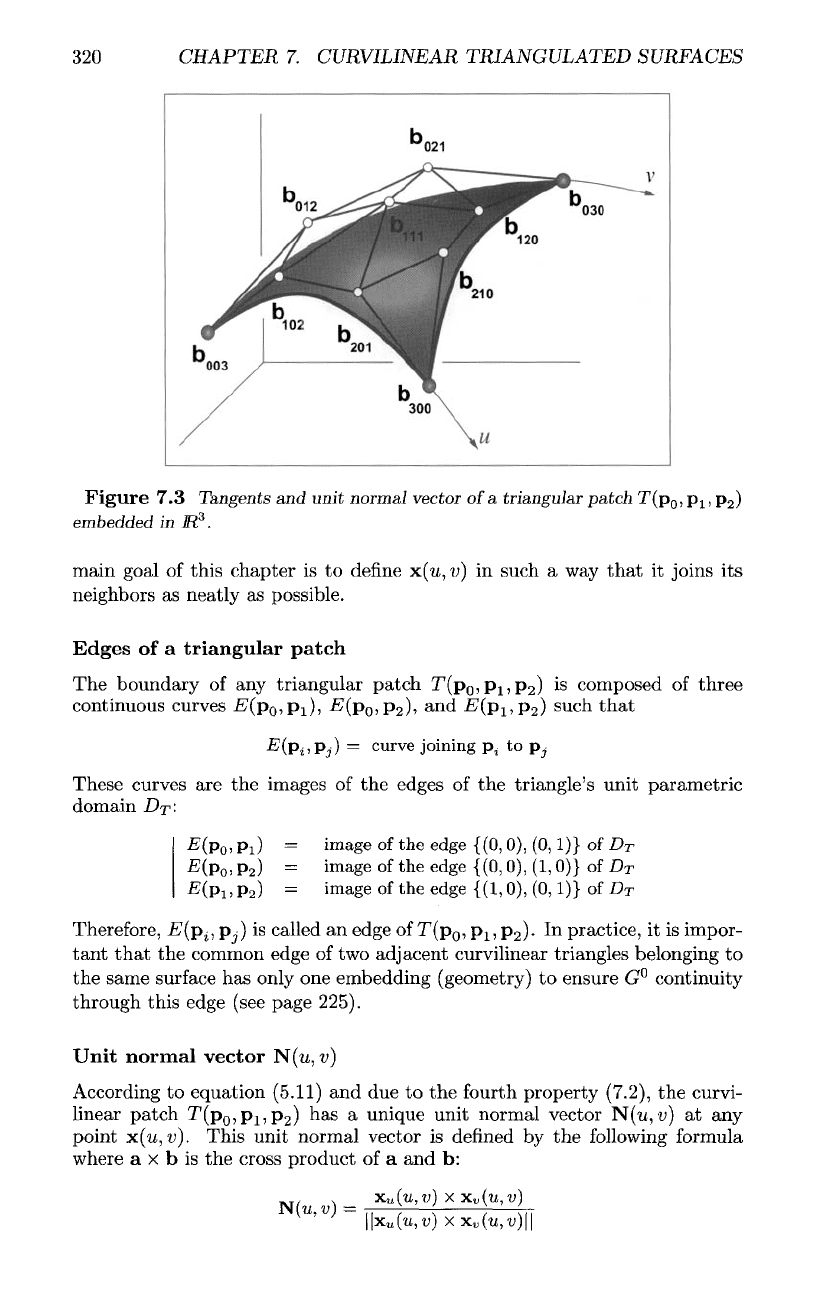
Figure
7.3
Tangents
and
unit normal vector
of
a
triangular
patch
T(p
0
,
p
l
,
p
2
)
embedded
in
iR
3
.
main goal
of
this chapter
is to
define
x(u,
v) in
such
a way
that
it
joins
its
neighbors
as
neatly
as
possible.
Edges
of a
triangular
patch
The
boundary
of any
triangular patch
T(p
0
,p
1
,p
2
)
is
composed
of
three
continuous curves
E(p
Q
^p
l
),
J
B(p
0
,p
2
),
and
£
T
(p
1
,p
2
)
such
that
These curves
are the
images
of the
edges
of the
triangle's unit parametric
domain
DT-
Therefore,
E(p
i
,
PJ)
is
called
an
edge
of
T(p
0
,
p
l5
p
2
).
In
practice,
it is
impor-
tant
that
the
common edge
of two
adjacent curvilinear triangles belonging
to
the
same
surface
has
only
one
embedding (geometry)
to
ensure
G°
continuity
through this edge (see page 225).
Unit
normal
vector
N(u,
v)
According
to
equation (5.11)
and due to the
fourth
property
(7.2),
the
curvi-
linear patch
T(p
0
,p
1
,p
2
)
has a
unique unit normal vector
N(u,
v) at any
point
x(w,
v}.
This
unit normal vector
is
denned
by the
following formula
where
a x b is the
cross product
of a and b:

7.2.
BUILDING
A
SMOOTH CURVILINEAR TRIANGLE
Figure
7.4
Data
available
for
interpolating
an
unknown
triangular
patch.
From
now on, the
normal vector
at the
three vertices
p
0
,
p
1;
and
p
2
of the
patch will
be
noted
as
N
0
,
N
x
and
N
2
,
respectively:
For
G
l
continuity
to be
assured,
it is
necessary
to
honor
the
continuity
of the
normal vectors through
the
common edge
of two
adjacent curvilinear triangles
belonging
to the
same smooth surface (see page 225).
7.2.2
Interpolating
a
triangular patch
Presentating
the
problem
As
shown
in
figure (7.4),
the aim is to
interpolate
an
unknown
triangular
patch
about which only
1.
the
locations
p
0
,
p
1;
p
2
of its
three vertices,
and
2.
the
unit
normal
vectors
N
0
,
N
l5
and
N
2
at its
three
vertices,
are
known.
There
is, a
priori,
an
infinity
of
continuously
differentiable
functions
x(u,
v)
generating
a
triangular patch
T(p
0
,
p
1?
p
2
)
that
respect these
data.
Hereafter,
only
functions x(u,v) having
the
following
general
form
will
be
considered:
The
functions
{wijk(u,
v)}
used
in
this equation
are
assumed
to be
given, while
the
points
{b;jfc}
have
to be
determined
as
functions
of the
data
(p
0
,N
0
),
(p^Nj),
and
(p
2
,N
2
).
321
322
CHAPTER
7.
CURVILINEAR TRIANGULATED SURFACES
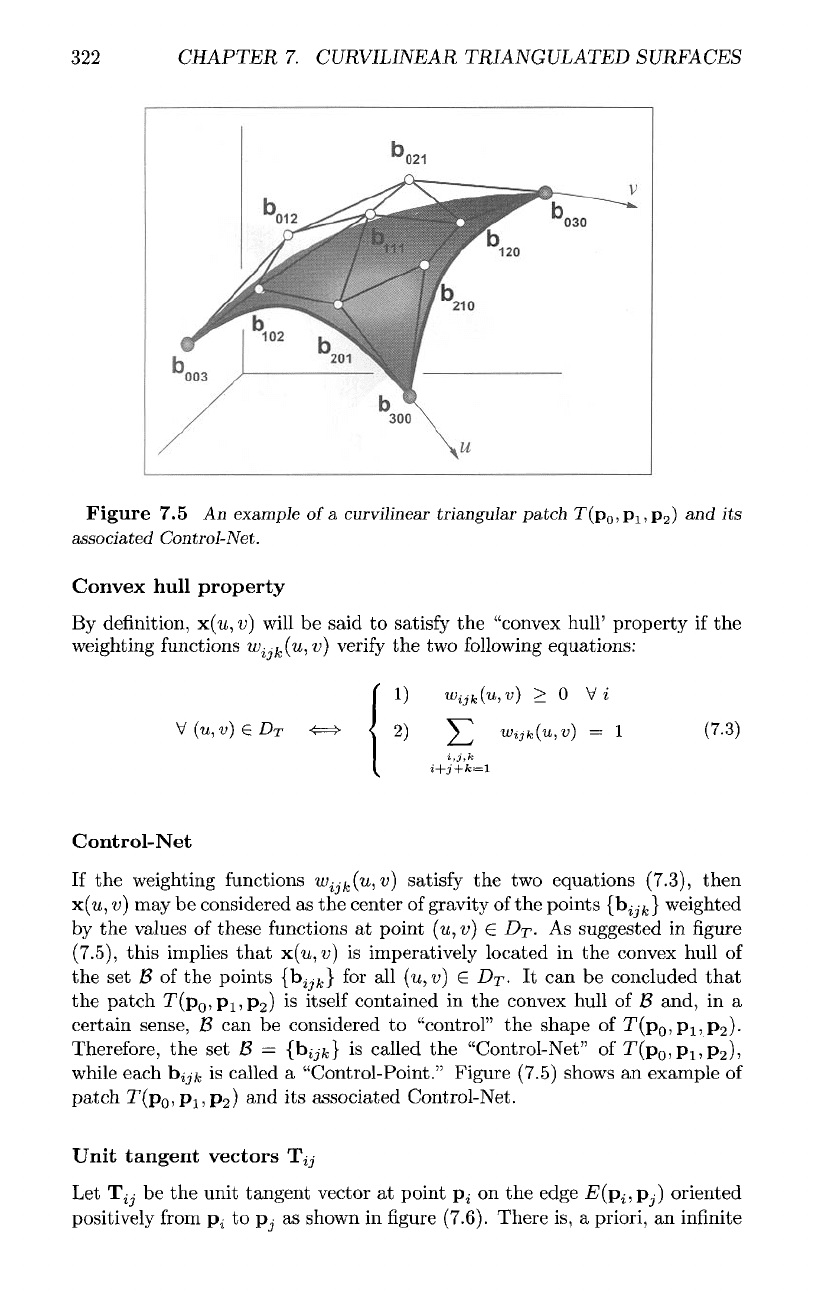
Figure
7.5 An
example
of
a
curvilinear
triangular
patch
T(p
0
,p
1
,p
2
)
and its
associated
Control-Net.
Convex
hull
property
By
definition,
x(it,
v)
will
be
said
to
satisfy
the
"convex
hull'
property
if the
weighting functions
w^
k
(u^v)
verify
the two
following
equations:
Control-Net
If
the
weighting functions
u^.
fc
(w,
v)
satisfy
the two
equations (7.3), then
x(w,
v)
may be
considered
as the
center
of
gravity
of the
points
{b^-
fc
}
weighted
by
the
values
of
these
functions
at
point
(u,v)
G
DT-
As
suggested
in figure
(7.5),
this implies
that
x(u,
v) is
imperatively located
in the
convex hull
of
the set
B
of the
points
{b^-
fc
}
for all
(u,v)
G
DT-
It can be
concluded
that
the
patch
T(p
0
,p
1
,p
2
)
is
itself contained
in the
convex hull
of B
and,
in a
certain sense,
B can be
considered
to
"control"
the
shape
of
T(p
0
,p
1
,p
2
).
Therefore,
the set B =
{bijk}
is
called
the
"Control-Net"
of
T(p
0
,p
1
,p
2
),
while
each
b^
is
called
a
"Control-Point." Figure (7.5) shows
an
example
of
patch
T(p
0
,p
1
,p
2
)
and its
associated
Control-Net.
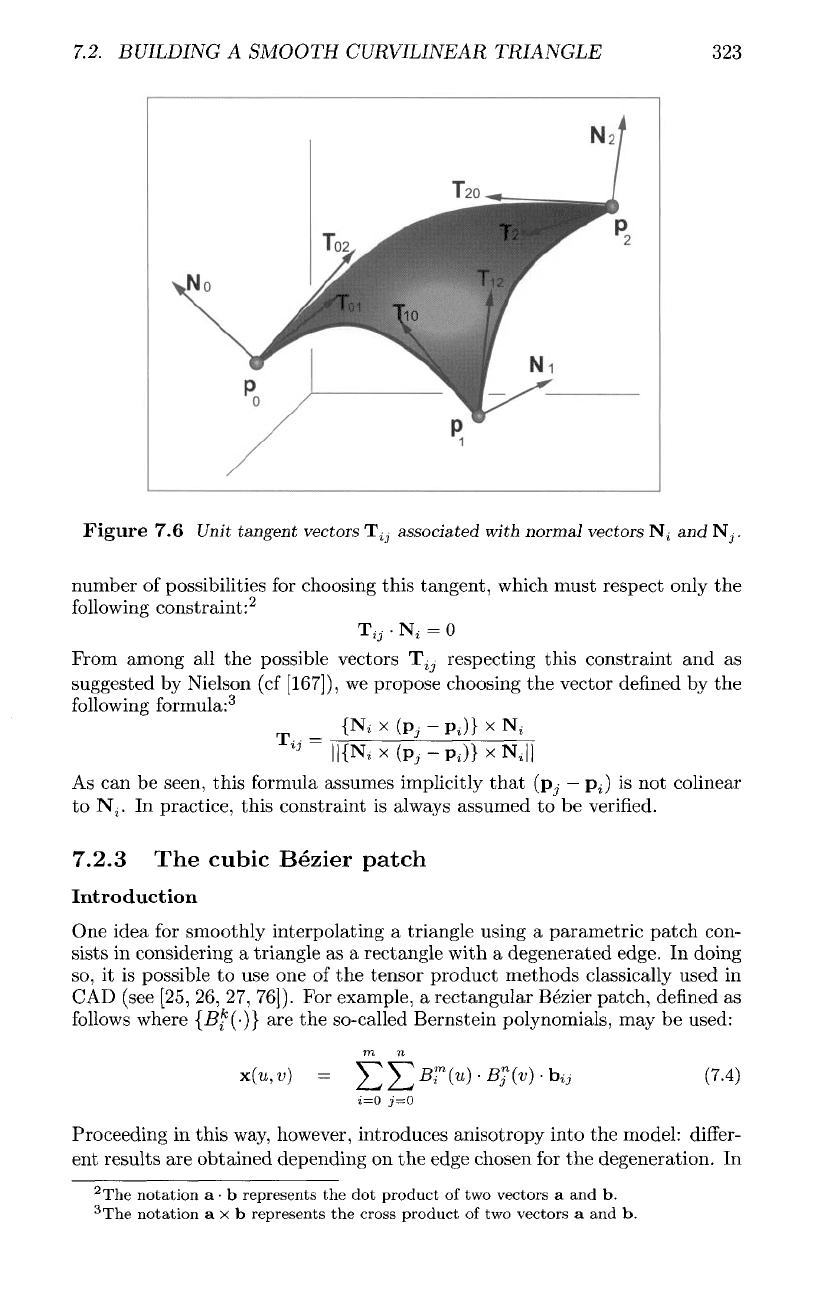
Unit
tangent
vectors
T^
Let
T^
be the
unit tangent vector
at
point
p^
on the
edge
E(p^
p
•)
oriented
positively
from
p^
to
p^
as
shown
in figure
(7.6).
There
is, a
priori,
an
infinite
7.2.
BUILDING
A
SMOOTH CURVILINEAR TRIANGLE
Figure
7.6
Unit
tangent
vectors
T^
associated
with
normal
vectors
Nj
and
N^.
number
of
possibilities
for
choosing this tangent, which must respect only
the
following
constraint:
2
From among
all the
possible vectors
T^
respecting this constraint
and as
suggested
by
Nielson
(cf
[167]).
we
propose choosing
the
vector
defined
by the
following
formula:
3
As
can be
seen, this
formula
assumes implicitly
that
(p^-
—
pj
is not
colinear
to
N^.
In
practice, this constraint
is
always assumed
to be
verified.
7.2.3
The
cubic Bezier
patch
Introduction
One
idea
for
smoothly interpolating
a
triangle using
a
parametric patch con-
sists
in
considering
a
triangle
as a
rectangle with
a
degenerated edge.
In
doing
so,
it is
possible
to use one of the
tensor product methods classically used
in
CAD
(see [25,
26, 27,
76]).
For
example,
a
rectangular Bezier patch,
defined
as
follows
where
{B^(•)}
are the
so-called Bernstein polynomials,
may be
used:
Proceeding
in
this way,
however,
introduces anisotropy into
the
model:
differ-
ent
results
are
obtained
depending
on the
edge chosen
for the
degeneration.
In
2
The
notation
a • b
represents
the dot
product
of two
vectors
a and b.
3
The
notation
a X b
represents
the
cross product
of two
vectors
a and b.
323

324
CHAPTER
7.
CURVILINEAR
TRIANGULATED
SURFACES
practice, building
a
smooth parametric representation
of a
curvilinear triangle
is
a
harder task,
and
tensor product methods
can no
longer
be
used
to
obtain
a
perfectly
symmetrical model relative
to the
three vertices
of the
triangle.
Barnhill [12],
in the first
article written
on
this
topic, proposed extending
the
Bernstein polynomials
in a
very
natural way:
• In the
univariate case,
the
Bernstein polynomials
Bf(u)
are
defined
as
the
terms
of the
binomial expansion
of (u +
w)
n
:
The
Bezier approximation
of a
curve
is
then
defined
as a
parametric
function
x(u)
that
depends
on (n + 1)
Control-Points
{bj
: i G [0,
n]}:
It is
relevant
to
note
that
(u,w)
can be
considered
as the
barycentric
coordinates
of a
point
on the
unit domain segment
[0,1].
•
Similarly,
in the
bivariate case,
the
Bernstein polynomials
B™Au,v]
are
defined
as the
terms
of the
trinomial expansion
of (u + v +
w)
n
:
As
illustrated
in figure
(7.5) where
n
=
3, the
Bezier approximation
of
a
triangle
is
defined
as a
parametric
function
x(w,
v]
that
depends
on
{(n
+ 1) • (n +
2)/2}
Control-Points
{b
ijk
:
i + j + k =
n}\
Note
that
(u,v,w)
may be
considered
as the
barycentric coordinates
(see
page 254)
of a
point
on the
triangle's unit parametric domain
DT as
defined
by
equation (7.1). Moreover,
for any
(u,v,w)
in
this
triangle's

unit parametric domain,
the
blending functions
(3™j
k
(u,v,w)
are
such
that
4
These properties guarantee
that
x(w,
v)
=
g(w,
v,
w)
will
be
located
in
the
convex hull
of the
Control-Points
bjjfc
as
long
as
(u,v,w)
remains
in
this triangle's unit parametric domain.
In
fact,
the
parametric representation
x(w,
v) can
also
be
viewed
as a
func-
tion
g(u,v,w)
of
three
not
independent
variables
w, v, and w
under
the
constraint
(u + v + w)
=
1:
This perfectly symmetrical parametric representation
of a
curvilinear Bezier
triangular patch
is at the
origin
of
most
of the
methods proposed
in the
literature
for
modeling curvilinear triangular
patches.
Prom
now on, for the
sake
of
simplicity, this system
of
symmetrical notations
will
not be
used,
and
x(w,
v)
will
be
considered
as the
parametric representation
of the
triangular
patch
to be
modeled. This implies using
a
different,
but
equivalent, notation
for
indexing
the
Control-Nodes.
For
example,
in the
case
of a
cubic Bezier
triangular patch,
the
"symmetrical
"
Control-Points
shown
in
figure
(7.5)
will
be
renumbered
as
indicated
in
figure
(7.7).
Bezier
Control-Net
83
The
cubic Bezier Control-Net
83
is
denned
as the set of
Control-Points
(p
0
,
Pn
P2>
Poi»
Pio>
Po2>
P20'
Pi2>
P2i>
Q>
shown
in
figure
(7.7)
and
defined
as
follows:
The
coefficients
(3-
are
assumed
to be
denned
as
The
choice
of the
positive
coefficient
/3
and the
function
0(-)
will
be
discussed
later
on
(see page 328).
4
This
is a
direct
consequence
of the
fact
that
the
values
{/3™-
k
(u,
v,
w)}
are the
terms
of
the
trinomial
expansion
of (u
+
v + w):
7.2 BUILIDING A SMOOTH CURVILINEAR TRIANGLE
325
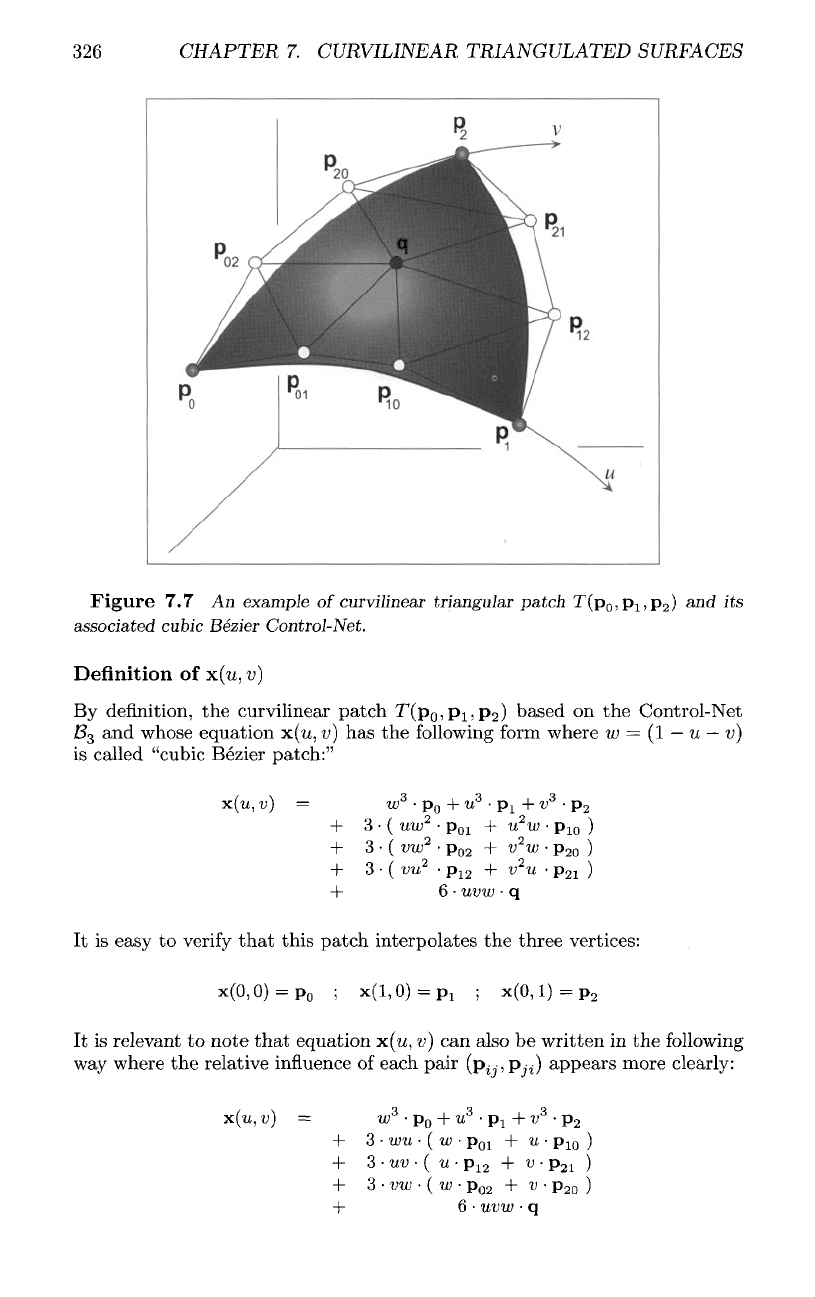
326
CHAPTER
7.
CURVILINEAR TRIANGULATED SURFACES
Figure
7.7 An
example
of
curvilinear
triangular
patch
T(p
0
,p
1
,p
2
)
and its
associated
cubic
Bezier
Control-Net.
Definition
of
x(u,
v)
By
definition,
the
curvilinear patch
T(p
0
,p
1
,p
2
)
based
on the
Control-Net
#3
and
whose equation
x(u,
v) has the
following
form
where
w
=
(I
—
u — v)
is
called "cubic Bezier
patch:"
It is
easy
to
verify
that
this patch interpolates
the
three vertices:
It is
relevant
to
note
that
equation
x(w,
v}
can
also
be
written
in the following
way
where
the
relative
influence
of
each pair
(p^-,Pjj)
appears more clearly:

7.2.
BUILDING
A
SMOOTH CURVILINEAR TRIANGLE
Derivatives
The
tangents
in the u and v
directions
can be
obtained
by
deriving
the
equa-
tion
x(w,
v) of the
cubic
Bezier
patch:
The
second-order derivatives
can
also
be
computed according
to the
following
formula:
Normals
at the
vertices
p
0
,
p
1?
and
p
2
If
the
tangents
at the
vertices
of
T(p
0
,
p
x
,
p
2
)
are
chosen
as
follows
then
it is
easy
to
verify
that
the
normal vector
N(w.
v}
interpolates
the
normal
vectors
N
0
,
N
1
and
N
2
at the
three
vertices
of the
patch:
327
