Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.

288
CHAPTER
6.
PIECE
WISE
LINEAR
TRIANGULATED
SURFACES
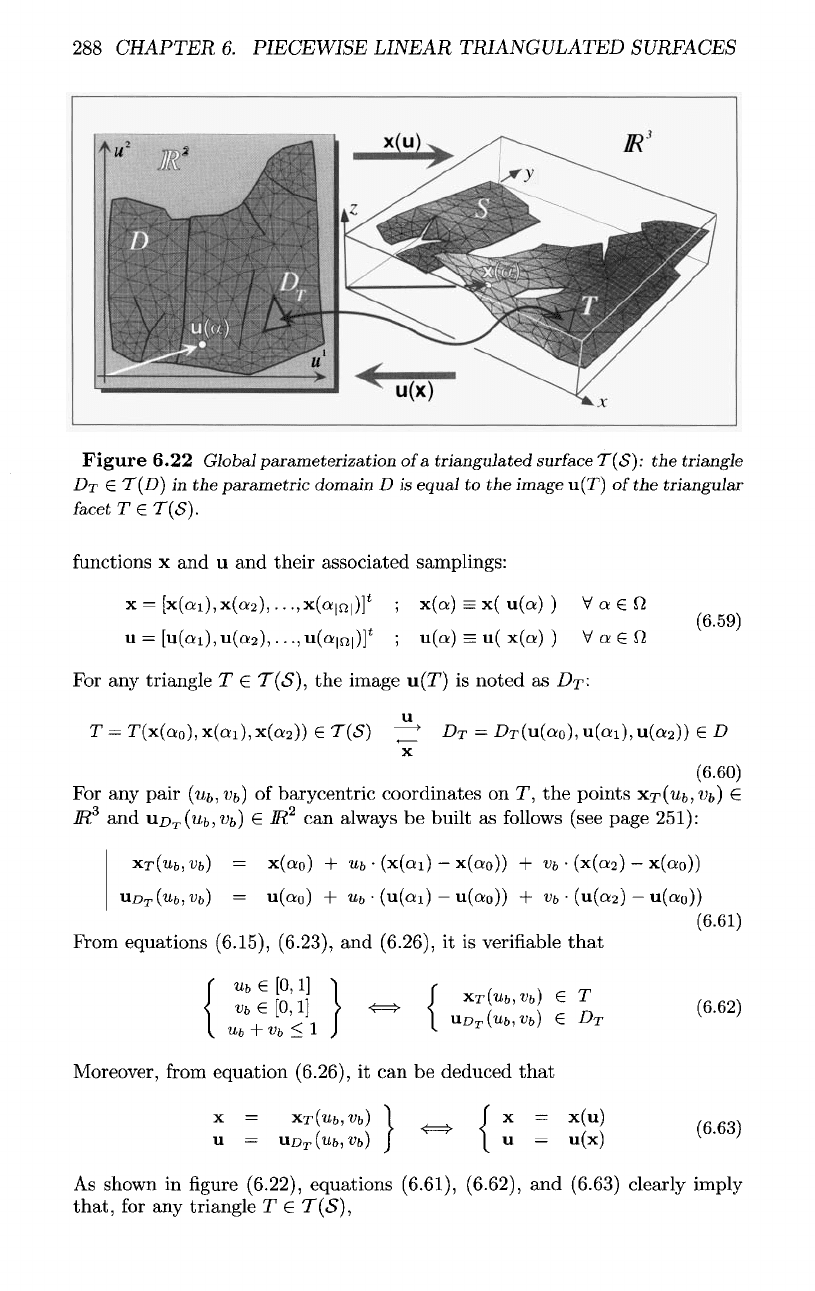
Figure
6.22
Global
parameterization
of
a
triangulated
surface
T(S):
the
triangle
DT
G
T(D}
in the
parametric
domain
D is
equal
to the
image
u(T)
of
the
triangular
facet
TeT(S).
functions
x and u and
their associated samplings:
For any
triangle
T G
T(<5>),
the
image
u(T)
is
noted
as
DT'-
For
any
pair
(ub,Vb)
of
barycentric coordinates
on T, the
points
XT^,^)
G
]R
3
and
urj
T
(ub,Vb)
G
7R
2
can
always
be
built
as
follows
(see page 251):
From
equations
(6.15),
(6.23),
and
(6.26),
it is
verifiable
that
Moreover,
from
equation
(6.26),
it can be
deduced
that
As
shown
in figure
(6.22),
equations (6.61),
(6.62),
and
(6.63)
clearly imply
that,
for any
triangle
T G
T(«S),

6.5.
GLOBAL
PARAMETERIZATION
• a
(flat)
rectilinear triangle
DT € D
corresponds
to the
(flat)
rectilinear triangle
T
e
T(5)
such
that
• the
vertices
of DT are the
images
of the
vertices
of T:
Moreover,
• the
parametric domain
D can be
modeled
as a
(flat)
triangulated
surface
T(X>)
such
that
• the
functions
x =
x(u)
and u =
u(x)
are
fully
determined
by
their values
on
the set
f2
of the
vertices
of
T(«S).
In
other
words,
assuming
that
the
facets
of
T(S]
consist
of flat
triangles,
the
problem
of
building
a
global
parameterization
u of S is
equivalent
to
determining
the
matrix
as a
function
of the
geometry
of S
itself defined
by the
following
matrix:
Discrete
model
X
2
(O,
N,
u,C
u
)
Assuming
that
the
facets
of
T(«S)
consist
of flat
triangles,
the
problem
of
determining
a
global
parameterization
of S is
equivalent
to
building
a
discrete
model
.M
2
(£7,
N, u,
C
u
)
where
u is the
matrix
as
defined
by
equation
(6.59).
Reducing
the
construction
of the
global
parameterization
to the
interpola-
tion
of a
vectorial
function
u =
[u
1
,
w
2
]*
defined
on the set of
nodes
of a
discrete
model
A^
2
(ri,
N, u,
Cu)
is a
great
step
forward. However,
such
a
problem
has
an
infinity
of
solutions
and
some
DSI
constraints
need
to be
added
to the set
C\i
to
specify
the
style
of the
particular
desired
solution.
In
practice,
as
will
be
seen
in the
sections
below,
two
types
of
constraints
will
be
considered:
• An
initial
set of
general constraints
will
be
introduced
for
specifying
that
the
triangulation
T(.D),
as
defined
by
equation
(6.64),
should look
like
a
"good"
map of
T(«S).
By
"good"
map of
T(«S),
we
mean
that
the
image
DT of any
triangle
T €
T(<S)
should approximately honor
the
following
constraints:
* the
triangles
T and DT
should have
the
same area;
* the
edges
of T and DT
should have
the
same length;
and
* the
angles
of T and DT
should
be
equal.
In
other words,
the aim is to
minimize
the
distortions between
T(«S)
and
its
image
T(D)
—
u(T(<S)).
These constraints
will
be
called "isometric con-
straints."
• A
second
set of
constraints
will
be
used
for
specifying
the
values
of u on
some
parts
of the
surface
S.
Such constraints
will
be
called "isoparametric
constraints."
289

290
CHAPTER
6.
PIECEWISE LINEAR TRIANGULATED SURFACES
From
a
theoretical point
of
view,
it can be
shown
that,
if the
locations
of two
distinct nodes
u(a)
and
u(a')
are fixed in
1R
2
,
and if the
isometric constraints
defined
above
are
used, then
the
global parameterization
u is
unique.
6.5.2
Isometric
constraints
A
preliminary
remark
Let
(u
l
,u
2
)
be the
components
of u and let
t
z
be the
unit
vector
19
colinear
to
grad
u
1
at
point
p G
S:
The
pair
(p,t*)
defines
a
straight line contained
in the
tangent plane
Tp(«S)
of
the
surface
S at
point
p and
which
has the
following
equation:
According
to the
definition
of the
notion
of
gradient (see equation
(5.23))
and
from
equation
(6.66),
it can be
observed
that
From
the
definition (6.66),
it can be
deduced
that
Taking equations
(6.66),
(6.67),
and
(6.68)
into account allows
us to
write
Comparing this equation with equation
(6.66),
it can be
concluded
that
the
following
relationship between
x
M
i
and
grad
u
l
holds true:
Notion
of
isometric
constraints
As
suggested
in figure
(6.22),
for
simplicity's sake,
the
parametric domain
is
traditionally assumed
to be
provided with
a
rectilinear
coordinate system
(u
l
,u
2
}
associated with
an
orthonormal
frame
(Ii,l2).
In
other words,
any
vector
u =
(u
1
,
u
2
)
of D can be
written
as
The
frame
(Ii,l2)
and its
associated
metric tensor
GO are
constant
over
D
and
it is
relevant
to
note
that
19
Note
that
u^
represents
a
scalar
value
and
thus
its
gradient
can be
computed.
6.5.
Thi s
implies
that,
in the
parametric domain,
the
following
metric properties
are
always honored:
• The arc
length
dsa
corresponding
to an
increment
(du
1
,
du
2
)
in the
parametric
domain
D is
such
that
• The
element
of
area
dAa
corresponding
to an
increment
(du
l
,du
2
)
in the
parametric domain
D is
such
that
• The
scalar product
of
two
vectors
a and b
belonging
to the
parametric domain
D and
defined
by
is
such
that
On
the
other hand,
if the
metric tensor
G
associated with
the
parametric
representation
x(u
1
,
u
2
)
of the
surface
<S
is
considered
then, according
to
equations
(5.15), (5.19),
and
(5.18),
the
following
local
metric properties
at
point
p =
x(u
1
,
it?)
on
<S
hold true:
• the arc
length
ds
corresponding
to an
increment
(du
l
,du
2
)
on the
surface
S
is
such
that
• the
element
of
area
dA
corresponding
to an
increment
(du
1
,
du
2
)
on the
surface
S is
such
that
• the
scalar product
of two
vectors
a and b
belonging
to the
tangent plane
Tp(S)
to S at
point
p =
x(ti
1
,u
2
)
and
defined
by
is
such
that
If
the
distortions between
the
triangulated
surface
T(S)
and its
image (map)
T(D]
in the
parametric domain have
to be
minimized
to
honor
the
con-
straints
(6.65),
then, according
to
equations
(6.70), (6.71), (6.72), (6.74),
(6.75), (6.76), (6.77),
and
(6.78),
the
parameterization
u has to be
built
so
that
GLOBAL PARAMETERIZATION
291

292
CHAPTER
6.
PIECE
WISE
LINEAR TRIANGULATED SURFACES
Taking equation
(6.69)
into account,
we can
conclude
that
the
parameteri-
zation
u
=
(M
1
,^
2
)
has to
honor
the
three
following
DSI
constraints, called
"isometric
constraints:"
Moreover,
in
addition
to
these constraints
and as
shown
in figure
(6.6),
it
is
wise
to add DSI
Constant-Gradient constraints
to
Cu
specifying
that,
for
any
pair
of
adjacent triangles
T and
T",
the
gradient
of
u
l
and
w
2
should
be
approximately constant:
As
can be
seen,
all
these constraints
are
clearly special cases
of
some
of the
general
purpose
DSI
constraints presented
in
section (6.2.1).
However,
special attention should
be
paid
to the
constraint (6.80)-3, which
must
be
applied both iteratively
and
alternately
as
follows,
but
only
as a final
step,
to
refine
the
parameterization:
//—
orthogonalisation
of
iso-it
1
and
iso-w
2
•
i<—
1
while
(
more
iterations
are
needed
) {
for_all(
a € ft ) {
•
install
a
constraint
on
u
l
specifying
that
gradu
1
must
be
orthogonal
to
gradu
3
~
l
} //-
end:
for_all
• run DSI on
u
l
•
i<—
(3
-
i)
} //-
end: while
It
should
be
noted
that
the
quality
of the
parameterization
is
strongly
de-
pendent
on the
quality
of the
initial solution used
in the
above algorithm;
as
an
example,
in
section
(6.5.3)
we
will
propose
an
algorithm capable
of
pro-
ducing
an
initial parameterization
that
approximately honors
the
isometric
constraints
(6.80).
Comment
1
If
the
isometric constraints
are
honored strictly, then
it is
easy
to
imagine
flattening the
surface
S
without
any
plastic deformation
and
putting this
flattened
version
in
coincidence with
its
parametric domain
D. In
other words,
if
the
isometric constraints
are
perfectly
honored, then,
• the
surface
S is
developable;
and
• any
segment
(u,
u')
in the
parametric
domain
is
transformed
into
a
geodesic
curve
(x(u),x(u'))
on the
surface
S
(see
page
216).
However,
as
already mentioned
(see
page 221),
a
surface
is
developable
if,
and
only
if, its
Gaussian curvature
K is
equal
to
zero everywhere,
and
this
is

6.5.
GLOBAL PARAMETERIZATION
generally
not the
case
in
practical applications. Consequently,
the
isometric
constraints
(6.80)
cannot
be
rigorously honored,
in
general,
and
have
to be
implemented
as
soft
DSI
constraints
to be
honored
in a
least square sense.
From
a
practical point
of
view,
this suggests modulating
the
certainty
factor
w
c
of any
soft
isometric constraint
c
locally
as a
function
of the
total
curvature
K of the
triangulated
surface
T(S).
For
example,
at
each node
a
of
T(<S)
where such
a
constraint
has to be
taken into account,
it may be
wise
to
modulate
w
c
as
follows
20
where
Dev(a)
is the
relative
developability-index
defined
by
equation
(5.59)
at
node
a of
T(<S).
Comment
2
Honoring
the
isometric constraints strictly
or in a
least square sense
is of
paramount importance
in
some practical applications.
For
example:
• In
structural geology (see section
(8.5)),
if S is a
folded/faulted hori-
zon
separating
two
sedimentary layers, then
the
operation
of
"unfold-
ing"
and
"unfaulting"<£
to
retrieve
its
initial shape prior
to any
tectonic
event
is
called
a
"palinspastic"
reconstruction. Generally, since
the
ini-
tial
shape
of a
horizon
can
reasonably
be
considered
as
planar, thanks
to the
isometric constraint,
the
parametric domain
D
=
u(<S)
can be
considered
as a
good approximation
of
this initial
flat
shape. This
re-
mark
is at the
origin
of an
unfolding
method presented
in
section (8.5).
• In
geostatistics
(see section
(9.7)),
there
are
many
situations
where
the aim is to
model
the
variations
of a
property
</?
attached
to a ge-
ological
surface (horizon
or
fault)
and
observed
on a set of
sampling
points
{p^}
scattered
on
<S.
In
this case,
all the
geostatistical
methods
rely
strongly (and implicitly)
on the
fact
that
the
shortest curvilinear
distance
21
d$(p,
q) on
<S
can be
computed
for any
pair
of
points
(p, q)
on
<S.
In
practice, thanks
to the
isometric constraints, these distances
can
actually
be
computed easily
in the
parametric domain
D:
2
Test
examples
DSI
constraints
ensuring
the
orthogonality
of the
iso-w
1
and
iso-w
2
curves,
together with
the
Constant-Gradient
constraints
and the
C°
and
C
1
pseudo-
continuity constraints
for the
u
l
and u
2
parameters,
are the key to the
isomet-
ric
global parameterization
of
triangulated surfaces.
The two
test
examples
proposed below allow
us to
evaluate
the
efficiency
of
these
DSI
constraints:
20
Note
that
Dev
belongs
to the
range
[0,1]
and the
modulated value
is
close
to
-c&
c
if the
surface
is
developable
in the
neighborhood
of a.
21
See
the
definition
of the
notion
of
geodesic
on
page 216.
293

294
CHAPTER
6.
PIECEWISE LINEAR TRIANGULATED SURFACES
Figure
6.23
Global
isometric parameterization
of
a
triangulated
surface.
•
Figure
(6.23)
shows
the
results
of the
isometric
DSI
constraints applied
to a
triangulated
surface
representing
a
face
(see
figure
(6.23)-A).
The
effect
of the
orthogonality
and
Constant-Gradient constraints
can be
brought
to the
fore
by
comparing
figure
(6.23)-B
(no
constraints used)
and figure
(6.23)-D
(orthogonality
and
constant gradient constraints
en-
forced),
where
a
checkered
pattern
22
is
mapped
to the
surface.
The
isoparametric curves corresponding
to
this latter image
are
displayed
in
figure
(6.23)-C,
where
one can
check
that
the
iso-w
1
and
iso-w
2
curves
are
orthogonal.
For all
four
of
these images,
the
C°
and
C
l
pseudo-
continuity constraints ensuring
the
continuity
of the
global parameter-
ization
through cuts have been
specified
at the
mouth
and the
eyes
of
the
model.
• In figure
(6.24),
a
geological surface representing
a
salt
dome
is
param-
eterized.
For
this kind
of
surface which
is far
from
being developable,
distortions
will
still remain,
and it may be
useful
to
choose
a
compro-
mise
between
the
orthogonality
and the
constant gradient
of the
iso-w
1
and
iso-u
2
curves.
For
this
purpose,
the
certainty factors
of
these
two
constraints
can be
used
to
modulate their relative importance:
22
A
checkered
pattern
parallel
to the
M
1
-coordinate
and
u
2
-coordinate
axis
in the
para-
metric domain
D is
texture mapped
[40,
82,
131]
on S by the
parametric equation
x(u).

6.5.
GLOBAL PARAMETERIZATION
Figur e
6.24
Modulating
the
orthogonality
versus
the
regular
spacing
of
isopara-
metric
curves.
—
In figure
(6.24)-A,
the
orthogonality
is
respected,
but
there
is a
great
variation
in the
size
of the
checkered
texture's
squares.
—
In figure
(6.24)-C,
the
squares
are of
approximately
the
same
size,
yet
the
isoparametric
curves
are far
from
being
orthogonal.
—
An
average
solution
is
shown
in figure
(6.24)-B,
where
the
same
certainty
factor
was
used
for the two
constraints.
6.5.3
Looking
for an
initial parameterization
As
already mentioned
on
page 292,
the
quality
of the
global parameterization
obtained
with
the
DSI
algorithm
is
strongly dependent
on the
initial
solution
and it is
thus
of
paramount importance
to
look
for an
initial parameterization
(u(a)
=
(w
1
(a),
u
2
(o)}
:
a
e
fi}
that
approximately honors
the
isometric
constraints (6.80). Among
the
many possible techniques
that
can be
used
for
building
such
an
initial solution,
in
this section
we
propose
an
approach based
on
the
concept
of
"conjugate" functions, which
has the
advantage
of
directly
taking into account
the
constraints
(6.80).
Notion
of
conjugate
functions
on a
triangle
T
Let
(p
be a
function
defined
on the set
£7
of
vertices
of a
triangulated
surface
T(<S),
and let T =
T(x(o!o)
5
x(ai)>x(a2))
be a
triangular facet
of
T(S).
As-
suming
a
linear variation
of
ip
on T
with
a
constant gradient
grad(/?JT,
it is
easy
to
check
23
that
the
values
(/?(ao),
^fai))
an
d
(
p(
a
2)
at the
vertices
of T
are
such
that
In
other words,
if the
value
(p(ot,i)
at one of the
vertices
of T is
known, then
the
values
of
(p
at the two
other vertices
can be
determined thanks
to the
above equation.
23
Taking
into account
the
fact
that
grad<^
is
constant
on T,
this
formula
is a
straight-
forward
applications
of
property
(5.23).
295
3

296
CHAPTER
6.
PIECEWISE LINEAR TRIANGULATED SURFACES
By
definition,
a
linear function
(p
defined
on T is
said
to be
conjugate
of
(p
on T if its
constant
gradient
grader
has the
same
length
as
grade/?\T
and
is
orthogonal
to
grad(/?|y:
If
we
note
NT the
unit
vector orthogonal
to the
triangle
T,
then
the
gradient
of
such
a
conjugate
function
(p
can be
deduced
from
grad</?|T
as
follows:
Moreover,
similar
to
equation
(6.81),
the
values
of
(p
at the
vertices
of T
honor
the
following
equation:
Building
an
initial
parameterization
It
should
be
noted
that
any
pair
of
conjugate functions
(<£>,
(p)
defines
an
isometric parameterization
of T =
T(x(a
0
),x(ai),x(a2))
provided
that
For
this
purpose,
it
suffices
to
define
U(CKO),
u(ai)
and
u(a
2
)
as
follows:
This suggests
the
following
seven-step algorithm
to
build
an
initial parame-
terization
of a
triangulated
surface
T(<$)
that
roughly honors
the
constraints
(6.80):
1.
Perform
the
following
initializations:
•
initialize
to
zero
a
"counting"
function
c and a
pair
of
functions
(ip,
(p)
denned
on the set
$1
of the
vertices
of
T(«S):
•
choose
an
initial
triangle
T
=
T(x(ao),
x(ai),x(a:2))
belonging
to
T(<S)
and set
c(ao)
equal
to 1:
•
choose
a
unit
vector
g
parallel
to T.
2.
Among
the
vertices
{ao,
0:1,
0:2}
of T,
look
for an
index
i
such
that
c(oa)
^
0.
If
there
is no
such
vertex,
then
go to
step
7;
otherwise
determine
(a,
(3)
such
that
3.
Compute
the
unit
vector
g =
NT
x g.

6.5.
GLOBAL PARAMETERIZATION
4.
Perform
the
following
operations:
24
5.
Build
the set
Ao(T)
of all the
triangles
neighboring
T
that
have
at
least
one
vertex
a
such
that
c(a)
— 0.
6.
If
Ao(T)
is
empty,
then
go to
step
7,
otherwise,
for
each
triangle
T* 6
Ao(T),
execute
recursively
the
following
operations:
•
rotate
g in
such
a way
that
g
becomes
parallel
to T*
• T
<—
T*
• go to
step
2
7.
For all a G
fi,
initialize
the
parameterization
u
=
(w
1
,?/
2
)
as
follows:
In the
case where
T(S]
is
affected
by
discontinuities
(e.g.,
fault
traces),
it is
necessary
for any
parameterization
to be
continuous through these disconti-
nuities.
Such
a
continuity
is
automatically ensured
if the
triangles linked
to
T by
"Vectorial-Links"
(see page 275)
are
added
to the set
Ao(T)
at
step
5
of
the
above algorithm.
6.5.4
Isoparametric
constraints
Definition
Let
us
consider
the
vectorial
function
u(x)
=
(w
1
(x),
w
2
(x))
defining
a
global
parameterization
of a
surface
S.
Each component
w
z
(x)
is a
scalar
function
denned
on S
and,
for any
given value
WQ,
the set of
points
J
I
(UQ)
as
defined
by
is
an
isovalue curve
of
w
l
(x)
drawn
on S. By
definition, such
a
curve
is
called
a
"^-isoparametric
curve"
of the
associated parameterization
x(u).
24
These
updating
formulae
are
straightforward
applications
of
equations
(6.81),
and
(6.82)
combined
with
the
fact
that
297
