Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.


268
CHAPTER
6.
PIECEWISE LINEAR TRIANGULATED SURFACES
Figure
6.9
Example
of
Control-Parallelism
constraint:
the
dark
surface
T(<S)
to be
modeled
has to
remain
as
parallel
as
possible
to a
given
surface
T(<$o)
while
honoring
any
other
DSI
constraints.
The
direction
of N and the
radius
p can be
modified interactively
to
specify
the
orientation
of the
tangent plane
and the
"flatness"
of S in the
neighbor-
hood
of the
projection
of p on
T(5)
in the
direction
N.
Fuzzy
Control-Parallelism
constraint
In
sedimentary geology,
the
horizons are, generally, more
or
less parallel.
As a
consequence, there
are
many
situations
where
we
want
to
model
a
geological
horizon
T(<$)
more
or
less parallel
to a
given
reference
horizon
T(«S
0
)
while
honoring
some other
DSI
constraints
if
any.
For
this purpose,
we
introduce
the
notion
of a
"Control-Parallelism" con-
straint
defined
as
follows:
•
Choose
a
direction
d.
Most
of the
time,
d is
chosen
as
being
equal
to the
vertical
direction,
but
this
is not
mandatory:
it is
even
possible
to use a field
of
non-constant
directions
d(o:).
• For
each
node
a of
T(<S),
determine
the
triangle
TO
of
T(<S
0
)
hit by the
straight
line
A(x(a),d)
passing
through
x(a)
and
parallel
to d, and
define
n(o:)
as
being
equal
to
-
either
"void"
if
A(x(a),d)
does
not
intersect
T(«S
0
),
—
or the
normal
vector
to TO if
A(x(a),d)
intersects
T(»5
0
).
•
Install
a
fuzzy
Control-Normal-Vector
constraint
for
each
node
a of
T(S)
where
n(a)
is
different from
"void."
Figure (6.9) shows
an
example
of
such
a
Control-Parallelism constraint, where
the
additional
constraints
consist
of one
Control-Node (small cube) plus Control-
Straightline constraints
specifying
that
the
boundary
of
T(«S)
must slide
on
vertical lines.
6.2.
BASIC
DSI
CONSTRAINTS
Figur e
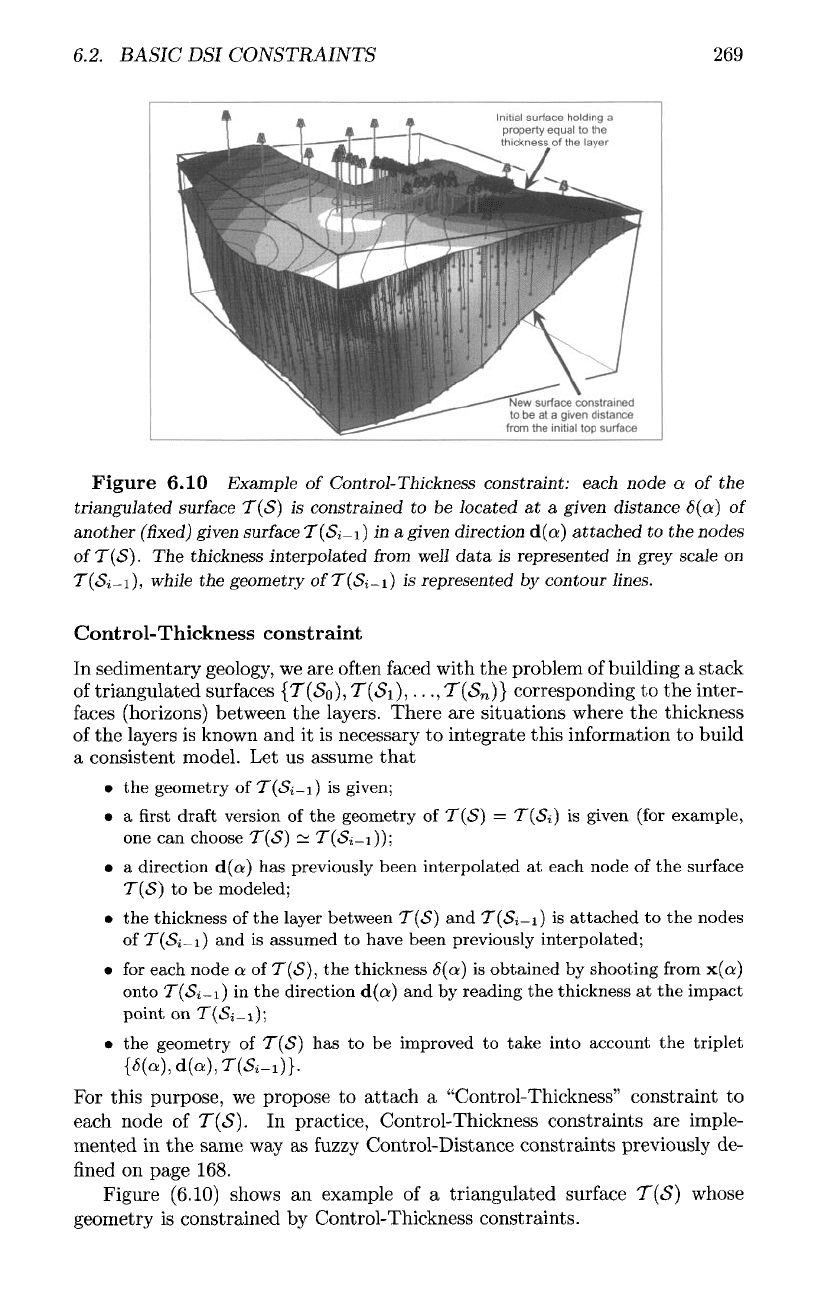
6.10 Example
of
Control-Thickness constraint:
each
node
a of the
triangulated
surface
T(*S)
is
constrained
to be
located
at a
given distance
8(ot)
of
another
(fixed)
given
surface
T(«Si_i)
in a
given direction
d(a)
attached
to the
nodes
ofT(S}.
The
thickness interpolated
from
well
data
is
represented
in
grey scale
on
T(«Si_i),
while
the
geometry
of
T(<Si_i)
is
represented
by
contour lines.
Control-Thickness
constraint
In
sedimentary
geology,
we are
often faced
with
the
problem
of
building
a
stack
of
triangulated
surfaces
(T(<So),
T(«$i),...,
T(S
n
}}
corresponding
to the
inter-
faces (horizons)
between
the
layers.
There
are
situations
where
the
thickness
of
the
layers
is
known
and it is
necessary
to
integrate
this
information
to
build
a
consistent
model.
Let us
assume
that
• the
geometry
of
T(Si-\)
is
given;
• a first
draft version
of the
geometry
of
T(«S)
=
T(<Sj)
is
given (for example,
one
can
choose
T(«S)
~
T(«Sj_i));
• a
direction
d(a)
has
previously been interpolated
at
each node
of the
surface
T(S}
to be
modeled;
• the
thickness
of the
layer between
T(«5)
and
T(«Si-i)
is
attached
to the
nodes
of
T(Si-\)
and is
assumed
to
have been previously interpolated;
• for
each node
a of
T(«S),
the
thickness
<5(a)
is
obtained
by
shooting
from
x(a)
onto
T(«Si_i)
in the
direction
d(a)
and by
reading
the
thickness
at the
impact
point
on
T(«Si_i);
• the
geometry
of
T(«S)
has to be
improved
to
take into account
the
triplet
{«(a),d(a),T(5i-i)}.
For
this
purpose,
we
propose
to
attach
a
"Control-Thickness"
constraint
to
each
node
of
T(S}.
In
practice,
Control-Thickness
constraints
are
imple-
mented
in the
same
way as
fuzzy
Control-Distance
constraints
previously
de-
nned
on
page
168.
Figure
(6.10)
shows
an
example
of a
triangulated
surface
T(S]
whose
geometry
is
constrained
by
Control-Thickness
constraints.
269

270
CHAPTER
6.
PIECEWISE
LINEAR
TRIANGULATED
SURFACES
Figur e
6.11
Example
of
Control-Segment constraint:
the
transparent triangu-
lated
surface
T(«S)
is
constrained
to
intersect
a set
of
segments.
Control-Segment
constraint
Let
us
consider
a
segment
cr(p,
d) of the 3D
space
denned
by a
point
p and a
vector
12
d in
such
a way
that
By
definition,
the
"Control-Segment"
constraint
associated
with
cr(p,
d) and
applied
to the
triangulated
surface
T(S]
will
be
said
to be
honored
if one of
the two
following
conditions
is
true:
•
either
the
straight line passing through
p and
colinear
to d
does
not
intersect
ns),
• or the
straight
line
passing through
p and
colinear
to d
intersects
T(S}
at a
point
(p + s • d)
such
that
s £
[0,1].
In
practice,
such
a
"Control-Segment"
constraint
is
implemented
as a
hard
DSI
constraint
(see
section
(4.5))
denned
as
follows:
• if the
straight
line
passing through
p
and
colinear
to d
does
not
intersect
T(S),
then
the
associated Control-Segment constraint
is
inactive;
• if the
straight
line
passing through
p and
colinear
to d
intersects
a
triangle
T -
T(x(o;o),
x(ai),
x(a
2
))
of
T(<S)
at a
point
(p + s • d)
such
that
s
G
[0,1],
then
the
associated
Control-Segment
constraint
is
inactive;
• if the
straight
line
passing through
p and
colinear
to d
intersects
a
triangle
T =
T(x(a
0
),x(ai),x(a!2))
of
T(<S)
at a
point
(p + s • d)
such
that
s
g[0,1]
then
the
triangle
T is
translated
in the
direction
d in
such
a way
that
- if s < 0,
then
the new
location
of T
contains
the
edge
p of the
segment
cr(p,
d), and
—
if s > 1,
then
the new
location
of T
contains
the
edge
(p + d) of the
segment
cr(p,
d).
12
Note
that
it is not
mandatory
for d to be a
unit vector.

6.2.
BASIC
DSI
CONSTRAINTS
Not e
that
this
kind
of
constraint
can be
extremely
useful
in
many
practical
applications;
for
example:
• if a
well-path does
not
intersect
a
geological
surface
T(<S),
then
a
Control-
Segment constraint associated with
the
segment
<r(p,
d)
should
be
installed
on
T(<5)
at
each point
p on the
well-path where
d is
such
that
• if the
intersection
of an
anticline
T(«S)
with
a
horizontal plane
Ji
must
be
constrained
to be
located inside
a
ring
7£
defined
by two
concentric polygonal
closed curves
Co
(TV)
and
Ci(JV)
contained
in
7i,
then
we
suggest proceeding
as
follows:
—
build
the
horizontal triangulated
surface
T(TV)
in
such
a way
that
the
only
nodes
of
T(TV)
are
those shared with
its
boundaries
Co
(TV)
and
Ci(fc);
—
for
each edge
(p
0)
Pi)
of
T(TV),
install
on
T(«S)
a
Control-Segment
con-
straint associated with
the
segment
<r(p
0
,p
1
—
p
0
).
For
example,
the
concentric curves
Co
(TV)
and
C\(TV)
may
correspond
to the
boundaries
of a
water contacts.
Figure
(6.11)
shows
an
example
of
triangulated
surface
T(S]
constrained
by
a set of
Control-Segments.
Control-no-Segment
constraint
A
"Control-no-Segment"
constraint
is the
logical
complement
to the
Control-
Segment
constraint
described
above.
By
definition,
the
Control-no-segment
constraint
associated
with
<r(p,
d) and
applied
to the
triangulated
surface
T(tS)
is
said
to be
honored
if one of the two following
conditions
is
true:
•
either
the
straight
line
passing
through
p and
colinear
to d
does
not
intersect
T(S}\
• or the
straight
line passing through
p and
colinear
to d
intersects
T(S]
at a
point
(p + s • d)
such
that
s
,£[0,
1].
Similar
to the
Control-Segment
constraint,
the
Control-no-segment
constraint
can be
implemented
as a
hard
DSI
constraint
defined
as
follows:
• if the
segment
cr(p,d)
does
not
intersect
T(<5),
then
the
associated Control-
no-segment constraint
is
inactive;
• if the
segment
cr(p,
d)
intersects
a
triangle
T =
T(X(Q;O),X(Q;I),
x(o!2))
of
T(«S)
at a
point
(p+s-d)
such
that
s
^[0,1],
then
the
associated Control-no-segment
constraint
is
inactive;
•
if
the
segment
cr(p,
d)
intersects
a
triangle
T =
T(X(QO),
x(ai),
x(ct2))
of
T(«S)
at a
point
(p + s • d)
such
that
s G
[0,1],
then
the
triangle
T is
translated
in
the
direction
d in
such
a way
that
—
if s <
|,
then
the new
location
of T
contains
the
vertex
p of the
segment
<r(p,
d), and
—
if s >
I,
then
the new
location
of T
contains
the
vertex
(p + d) of the
segment
cr(p,
d).
271

272
CHAPTER
6.
PIECE
WISE
LINEAR
TRIANGULATED
SURFACES
Figur e
6.12
The
intersection
of a
surface
S by a
fault
J-~
(not represented)
generates twin boundaries
/3(S/J-)
and
/3
f
(S/F)
that were coincident
before
the
displacement
along
the
fault
due to a
tectonic event.
6.3
Modeling
a
faulted
surface
Any
geological
surface,
such
as, for
example,
a
horizon,
an
unconformity,
or
even
an
older
fault,
can be
intersected
by a
fault.
In
practice,
three
different
actors
have
to be
considered
when
modeling
a
faulted surface:
• the
"faulted
surface,"
noted
as S
throughout this section;
• the
"fault," noted
as
F
throughout this section,
which
is a
surface playing
the
role
of a
cutter
that
generates both
a
geometric
and a
topological discontinuity
in
the
faulted
surface;
and
• the
"fault
trace," noted
as
B(S/J
r
)
throughout this section, which consists
of
a
curve corresponding
to the
boundary
of the
faulted surface
in
contact with
the
fault.
As
shown
in
figure
(6.12),
a
fault
trace
B(S/F)
is
itself
decomposed
into
twin curves
(3(S/F)
and
f3'(S/J-}
that
were coincident
before
the
fault
displacement:
From
the
faulted surface
S
point
of
view,
a
fault
T
can be
considered
in two
contradictory
ways:
• A
fault
is a
discontinuity
applied
to the
topology
and the
geometry
of the
faulted
surface,
and
this discontinuity induces
two
types
of
DSI
constraints:
—
The first
type
of
constraint
has to be
defined
to
guarantee
that
the
fault
trace
B(S/
F]
honors
the
relative displacements (throw vector)
on the
"twin
parts"
of the
faulted
surface
located
on
both sides
of the
fault.
—
The
second type
of
constraint
has to be
defined
to
ensure
the
junction
of
the
boundary
of the
faulted surface with
the
fault that intersects
it:
if
a
fault
F
intersects
the
faulted
surface
S
along
the
fault
trace
B(S/J-)
of
<S,
then
B(S/J-}
must remain stuck
to the
fault
J-'.

6.3.
MODELING
A
FAULTED SURFACE
Figur e
6.13
Parameterizing
the
twin
fault
traces
(3(S/F)
=
{P(0),P(1)}
and
P'(S/F]
=
{P'(0),P'(1)}
belonging
to a
triangulated faulted
surface
S.
•
Most
of the
time, physical properties attached
to a
faulted surface
S
(for
example,
a
seismic
reflectivity)
were
continuous
on
this faulted
surface
prior
to the
intersection
by the
fault,
and
this continuity
has to be
preserved. Prom
this standpoint,
a
fault
must
be
seen
as a
kind
of
"hyperlink" between
the
twin
curves
j3(S/F}
and
(3'(S/T}
located
on
both sides
of the
fault,
and
this
induces
two
types
of
DSI
constraints:
—
The first
type
of
constraint
has to be
defined
to
preserve
the
continuity
of
the
values
of the
properties through
the
fault
(C°
pseudo-continuity).
—
The
second type
of
constraint
has to be
defined
to
preserve
the
conti-
nuity
of the
gradient
of the
properties through
the
fault
(C
1
pseudo-
continuity).
6.3.1 Modeling fault-throw vectors
Notio n
of
twin
points
Consider
a
fault
trace
B(S/J
::
}
=
j3(S/F}
U
(3'(S/F}.
As
already
mentioned,
the
twin
curves
j3(S/J
:
}
and
f3'(S/J
:
}
are
assumed
to
have
been
coincident
before
the
displacement
along
the
fault
induced
by a
tectonic
event.
This
implies
that,
to any
point
p
belonging
to
/3(S/J
=
'),
there
corresponds
a
twin
point
p'
belonging
to
f3'(S/J
:
}.
Let
P(s)
and
P'(s)
be
parametric
representations
of
(3(S/J-}
and
f3'(S/J-}
assumed
to be
chosen
in
such
a way
that
the two
following
constraints
are
honored:
• The two
parametric curves P(s)
and
P'(s)
use the
same
parameter
s and
273

274
CHAPTER
6.
PIECEWISE LINEAR TRIANGULATED SURFACES
•
P(s)
and
P'(s)
were
assumed
to be
coincident
before
the
displacement
along
the
fault
due to a
tectonic
event.
As
suggested
in
figure
(6.13), most
of the
time, P(0)
=
P'(0)
and
P(l)
=
P'(l),
but
this
is not
mandatory (see
figure
(6.13)).
For
the
rest
of
this chapter,
it
will
be
assumed
that
each
of the
twin curves
(3(S/^F}
and
(3'(S/F)
can be
digitized into
(ra
+1)
equally spaced twin points
(P(sj)
: i =
0,m}
and
(P'(sj)
: i =
0,rn}
in
such
a way
that
Si =
i/m.
As
shown
in figure
(6.13),
it is
then possible
to
create
a
polygonal curve
D(A)
corresponding
to a set A of
(m
+ 1)
nodes
<5;
whose
locations
D
(<*);)
in the 3D
space
are
defined
by
Discrete
model
.A/f
3
(A,
N
A
,T,C
r
)
The
introduction
of the
polygonal curve
D(A)
enables
us to
define
a
discrete
model
.M
3
(A,
AT
A
,r,C
r
)
where
•
N&(Si)
is the
neighborhood
of the
node
Si
composed
of one or two
nodes
directly
linked
to Si on the
polygonal
curve
D(A);
•
r(6i)
=
{r
x
(8i),T
y
(8i),r
z
(8i)}
corresponds
to the
three
components
of the
specified
throw
vector
r(Si)
at
node
Si € A. It is
important
to
note
that
each
specified
throw
vector
r(<5j)
may be
different
from
the
corresponding
current
throw
vector
T(SJ),
as
defined
by
•
C
r
is a set of
constraints
associated
with
a
subset
LA of A and
specifying
that
the
throw
vectors
{r(l)
:
i
e
LA}
are
known.
This
subset
LA
must
be
considered
to be a set of
Control-Nodes
by the
DSI
algorithm
when
applied
to
.M
3
(A,
N&,T,C
T
}.
The
vectors
{r(i}
:
t
e
L
A
}
are
called
"Control-Throw"
vectors
and are
represented
as
double,
bold
arrows
in figures
(6.18),
(6.19),
and
(6.20).
From
a
graphical point
of
view,
for
each node
6i of the
polygonal line
D(A),
two
opposite segments (without arrow)
r
+
(6i)
and
T~(Si)
called "half throws"
can
be
drawn such
that
As
shown
in figures
(6.13), (6.18),
and
(6.19),
the
drawing
of the
segments
r
+
(6i)
and
r~(6i]
attached
to
nodes
6i
allows
the
specified
throw vectors
r(8i)
to be
visualized
in a
natural way.

6.3.
MODELING
A
FAULTED
SURFACE
275
Specifying
the
throw
As
mentioned above,
a
distinction
has to be
made between
the
current
set
of
throw vectors
{T(SJ)
: i = 0, ra} and the set of
specified
throw vectors
[r(di)
:
6i 6
A}
to be
honored
by the
faulted
surface.
The
specified
throw
vectors
may be
different
from
the
current throw vectors
and a
tool
is
necessary
to
allow
the
geologist
to
shape
the
specified
throw vectors interactively.
For
this purpose,
we
propose proceeding
as
follows:
• set the
Control-Throw
vectors
{r(l)
:
I
£
LA}
represented
as
double
bold
arrows
(see
figure
(6.18))
interactively,
and
next
consider
them
as fixed for
the
DSI
algorithm;
and
•
apply
the DSI
algorithm
to
.M
3
(A,
JVA,
T,
C
T
)
for
interpolating
the
unknown
values
{r(i)
:
i 6
/A}
where
/A
— A
—
I/A.
This procedure allows
the set of
specified
throw vectors
{r(8i)
:
6i 6
A}
to be
shaped
efficiently.
As
shown
in figure
(6.19),
these
specified throw
vectors
are,
in
general,
different
from
the
current
set of
throw vectors
(T(sj)
: i = 0,
m}.
6.3.2
Geometry
of a
faulted
surface
Discrete
model
.M
3
(0,7V,x,C
x
)
The
triangulated surface
T(«S)
is
assumed
to be
affected
by (at
least)
one
fault
whose
throw vectors
are
represented
by a
discrete model
A
/
f
3
(A,
N&,
T,
C
T
).
We
would like
to add
some
new
constraints
{c',
c",...}
to the set of
constraints
C
x
operating
on the
geometry
of
T(S]
to
•
Confine
the
current
throw
vectors
of
T(S)
to be as
close
as
possible
to the
specified
throw
vectors
held
by
A4
3
(A,
./VA,
T,
C
T
).
By
definition,
this
kind
of
DSI
constraint
will
be
called
a
"Vectorial-Link"
or,
more
simply,
a
"VecLink."
•
Maintain
the
consistency
of the
fault
trace,
by
specifying
that
the
curves
/3(S/J
r
)
and fi' (S/
F]
must
be
located
on the
fault
T'.
By
definition,
this
kind
of
DSI
constraint
will
be
called
a
"Boundary-on-Surface."
The
next
two
sections show
how to
build each
of
these
geometrical
DSI
con-
straints.
Vectorial-Link
constraint
Let
us
consider
a
specified
throw vector
r(6i)
and its
associated current throw
vector
T(SJ)
corresponding
to
twin points
P(S;)
and
P'(SZ)
on the two
sides
of
the
fault
(see
figure
(6.13)).
We
would
like
to add a set of new
constraints
|c',
c",.
• •}
t°
the set
Cx
specifying
that
For
this
purpose,
as
shown
in figure
(6.13),
let us
assume
that
P(SI)
belongs
to the
edge
(0:0,0:1)
°f
T(S}
P'(si)
belongs
to the
edge
(a'
0
,a'i)
of
T(S]
If
x(o:)
represents
the
location
of any
node
a £ 0,
then
the
relative locations
of
P(SI)
and
P'(SJ)
on the two
edges
(o;ojQ;i)
an
d
(aQ,a(),
respectively,
can

276
CHAPTER
6.
PIECEWISE LINEAR TRIANGULATED SURFACES
be
characterized
by the
parameters
13
Ui G
[0,1]
and
u^
€
[0,1],
as
defined
by
Using
parametric linear interpolations
on
edges
(ao,ai)
and
(a^o^)
makes
it
possible
to
write
This implies
that
the new
constraints
{c
f
,
c",...}
to be
determined should
be
such
that
In
other words,
for any i
e
[0,
m],
the
following
constraints should
be re-
spected:
As
suggested
in figure
(6.13),
for
each index
i
e
[0,
m],
theese three equations
can be
transformed into three
DSI
constraints
{cf,
q',
cf}
that
depend
on the
following
parameters
and are
defined
by
In
this
definition
of the
above constraint
c, the
coefficients
{^(o:)}
are all
assumed
to be
equal
to
zero except when
a is
equal
to
ao,
ai
or
a'
0
,
a(,
and
the
coefficient
a
c
is a
normalizing factor (see equation
(4.4))
chosen
as
follows
to
guarantee
that
\\A
C
\\
=
1:
For
simplicity's sake,
6^(x)
is
defined
as
follows:
13
Note
that,
for
example,
Ui and (1
—
Ui) are the
barycentric
coordinates (see page 254)
of
P(SI)
relative
to
x(ao)
and
x(ai).

6.3.
MODELING
A
FAULTED
SURFACE
277
Figure
6.14
A
horizon
S has
been
cut by
fault
J-
and
then
a
Boundary-on-Surface
DSI
constraint
has
been installed
between
the
horizon
<S
and the
fault
J-.
When
running
DSI on the
geometry
of
<S,
such
a
constraint
preserves
the
contact
between
the
fault trace
P(S/F]
and
F.
When added
to the set
of
constraints
C
x
of
the
discrete model
.M
3
(Q,
N,
x,
Cx),
the
above
DSI
constraints induce
the
following
terms
7^(0:)
and
T^(a
x) at
nodes
a =
OCQ
and a =
a\
in the
local
form
of the DSI
equation:
Similar
terms
7^(0;)
and
r£(a|x)
are
induced
14
at
nodes
a.
=
a'
0
and a =
a±:
Boundary-on-Surface
constraint
As
suggested
in
figures
(6.14),
and
(6.34),
let
(3(S/F]
be a
fault
trace gener-
ated
by the
intersection
of a
surface
S by a
fault
T.
From
a
geological point
of
view,
^(S/F}
must remain stuck
to
F
even
if the
shape
of S or
JF
is
modified.
In
other words,
the
discrete model
.M
3
(O,
TV,
x,Cx)
associated with
T(<S)
has
to be
constrained
in
such
a way
that
14
Pay
attention
to the
signs
'+' and '
—',
which
may
have changed.
