Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.


248
CHAPTER
6.
PIECE
WISE
LINEAR TRIANGULATED SURFACES
The
geometry
x, the
parameterization
u and the
properties
(p
—
(v?
1
,...,
<p
n
}
of
such
a
triangle
are
assumed
to be
denned
at the
vertices
(x(ao),
X(CKI),
x(o!2)
by the
discrete
models
M
3
(ft,
A/",
x,
C
x
),
M
2
(ft,
N, u,
C
u
),
and
.M
n
(ft,
AT,
<p,
C^,).
In
practice,
x, u and
(p
must
be
interpolated locally
on
each triangle
T £
T"(«S),
and the
next section shows
how to
build such local interpolants
in the
linear
case.
6.1.2
Triangular
piece
wise linear model
Loca l
parameterization
According
to
section
(5.2),
any
triangle
T =
T(x(o!o),x(ai),x(a!2))
of a
tri-
angulated
surface
T(«S)
is, in
itself,
a
surface
with
its own
local
parametric
equation
x^(u,
v]
such
that
There
is an
infinity
of
such possible parameterizations,
2
and
these
local
pa-
rameterizations should
not be
confused
with
the
notion
of
global
parameter-
ization
x(u)
=
x(w
1
,u
2
)
introduced
in the
previous
section.
The
same local parametric coordinate system
(w,
v) can be
used
not
only
for
modeling
the
variations
of the
geometry
X
T
(U,
i>),
but
also
for
modeling
the
variations
of any
function
(p
T
(u,
v)
attached
to a
triangle
T of
T(«S).
Linear
model
For
simplicity's sake,
in the
rest
of
this chapter,
it is
assumed
that
any
func-
tion
<p
T
(u,
v)
denned
on a
triangle
T
=
T(x(ao),
x(ai),
x(a2))
of
T(«S)
varies
linearly
on
D
T
:
If
(p
T
=
[c^rp,
• •
-5
^T]*
^
S
an
^--dimensional
vectorial
function,
then
the
param-
eters
(ao,
ai,
02}
are
vectors
of
lR
n
,
and
these
vectors
are the
solution
of the
following
linear system
where
(ui,Vi)
and
o^
are
denned
by
2
Section
(6.1.3)
presents some examples
of
such
local parameterizations used
in
practical
applications.
6.1.
INTRODUCTION
249
Provided
that
the
triangle
T is not
degenerated,
the
inverse
[Mr]"
1
exists
and is
such
that
Prom
equations
(6.2),
and
(6.3),
it can be
deduced
that
In
particular,
this
implies
that
the
derivatives
of
<p
on T are
defined
by
If
A
u
(cti\T)
and
A
v
(aj|T)
are
denned
as
follows
then
it can be
observed
that
the
derivatives
of
</?T
are
constant
on T and
such
that
Linear
triangular patch
In
practice,
as
shown
in figure
(6.1),
the
linear model introduced above
for
modeling
the
variations
of a
function
(p?
denned
on a
triangle
T of a
triangu-
lated
surface
T(S)
can
also
be
used
for
modeling
the
geometry
of T. In
this
case,
each triangle
T =
T(x(o;o),
x(o?i),
x(a2))
of
T(S]
is a flat
triangle called
a
"linear triangular patch" represented
by the
following
equation:
3
3
It
will
be
shown
in
chapter
7
that
it is
possible
to
build
curvilinear
patches
where
this
linear
equation
is
replaced
by a
nonlinear
equation, such
as, for
example,
a
polynomial
or
a
rational polynomial.
249

250
CHAPTER
6.
PIECEWISE LINEAR TRIANGULATED SURFACES
It can be
observed
that
the
derivatives
(X.T)U
and
(XT)
V
of
xy(u,
t?)
relative
to u and
i;
are
constant
on T and can
easily
be
deduced
from
the
geometry
of
T
thanks
to the
following
equation where
Ay
represents
the
matrix
defined
by
equations
(6.7),
and
(6.9):
In the
rest
of
this book,
the
following
notations
will
be
used where
GT is the
constant metric tensor associated with
the
local parameterization
(u,
v]
of T:
In the
case where
</?T
is a
scalar
function
(n
= 1),
according
to
equation
(5.21),
the
gradient
of
(p?
at
(u,v)
is
defined
by the
following
equation:
Taking
into account equations (5.21),
and
(6.9),
the
notations (6.11) enable
us
to
conclude
that
the
following
property holds true
for any
scalar
function
(f>T
defined
on a
triangle
T =
T(x(ao),x(o:i),x(a;2))
of
T(<5):
Consequently,
the
(contravariant) components
(gradc/>r)
u
and
(grad^r)^
of
the
vector
gradc^
relative
to the
frame
{U,
V}
are
such
that
In
this equation,
the
coefficients
{grad%>(a>i)}
and
{gratff
r
(a.i}}
depend only
on
the
geometry
of the
triangle
T and are
defined
by the
following
equation:

6.1.
INTRODUCTION
Figur e
6.2
Linear
parametric
interpolation
XT(U,V)
of a
triangle
T =
T(x(ao),x(o!i),
x(a!2))
based
on
barycentric
coordinates
(u,v).
6.1.3
Examples
of
local
linear
parameterizations
Barycentric
parameterization
of a
triangle
As
suggested
in
figure
(6.2),
the
"barycentric" parameterization
x^(w,v)
of a
triangle
T =
T(x(o!o),x(a:i),x(a!2))>
is
defined
by
It is
easy
to
check
that
the
associated domain
DT
does
not
depend
on T and
is
such
that
Moreover,
the
above "barycentric" parameterizations
x^(w,
v)
can
also
be
written
in the
following
way:
It can be
observed
that
X.T(U,V)
so
defined
honors
the
following
equations:
from
which
it can be
deduced
that
the
coordinates
(ui,Vi)
defined
by
equation
(6.4)
are
such
that
251
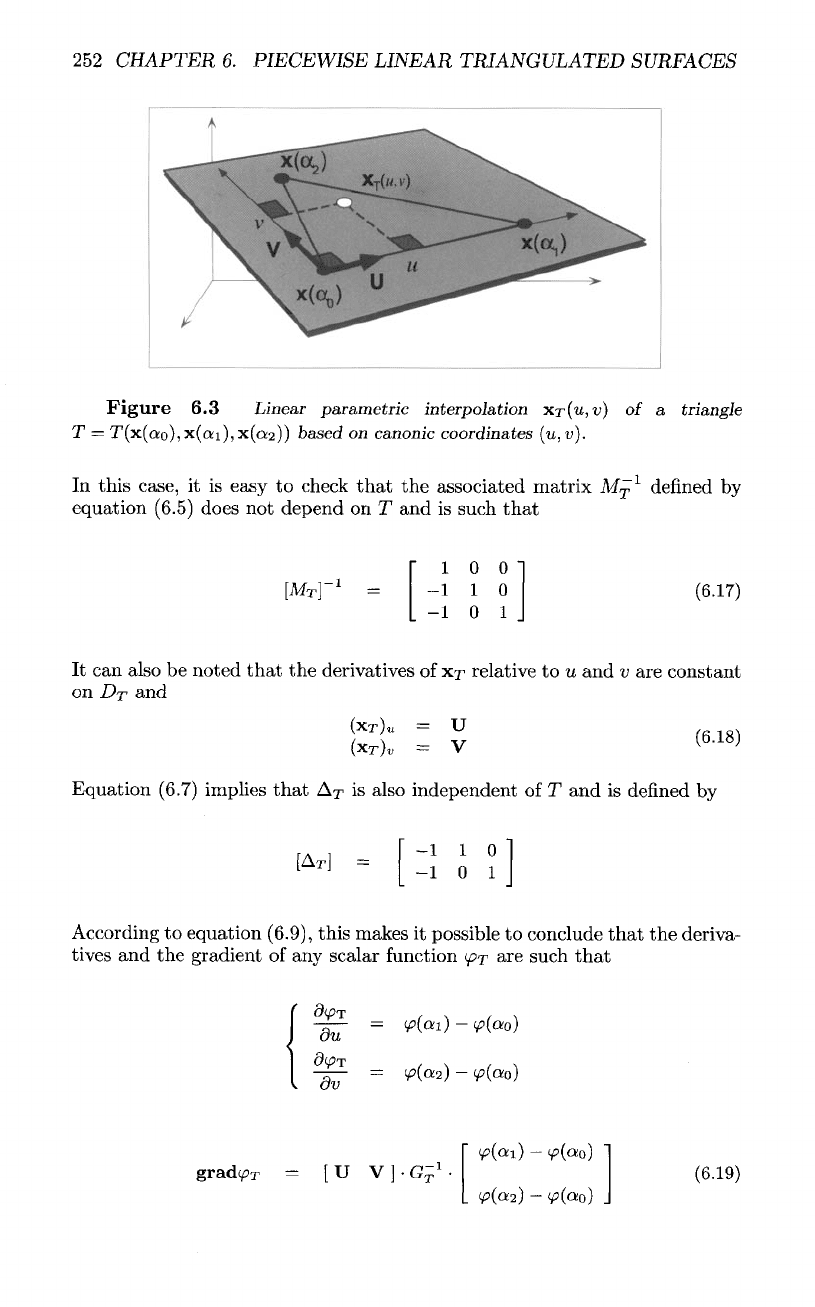
252
CHAPTER
6.
PIECE
WISE
LINEAR TRIANGULATED SURFACES
Figure
6.3
Linear
parametric
interpolation
XT(W,
v) of a
triangle
T =
T(x(ao),x(o!i),x(Q2))
based
on
canonic
coordinates
(u,v).
In
this case,
it is
easy
to
check
that
the
associated matrix
M^
1
defined
by
equation (6.5) does
not
depend
on T and is
such
that
It can
also
be
noted
that
the
derivatives
of
XT
relative
to u and v are
constant
on DT and
Equation (6.7) implies
that
AT is
also independent
of T and is
defined
by
According
to
equation
(6.9),
this makes
it
possible
to
conclude
that
the
deriva-
tives
and the
gradient
of any
scalar
function
if>
T
are
such
that

6.1.
INTRODUCTION
Canoni c parameterization
of a
triangle
As
suggested
in figure
(6.3),
the
"canonic" parameterization
XT(U,V)
of a
triangle
T
=
T(x(ao),x(o!i),x(Q!2))
is
defined
by
4
The
associated
matrix
M^
1
defined
by
equation
(6.5)
can
easily
be
deduced
from
the
coordinates
(w^,
Vi)
of the
vertices
of the
triangle
T, as
defined
by
It is
relevant
to
note
that
the
derivatives
of
XT
relative
to u and v are
constant
on
DT and
such
that
According
to
equation
(6.20),
this means
that
{(XT)
U
,
(
X
T)V}
is
an
orthonor-
mal
frame,
and the
associated metric tensor
GT is
thus such
that
Prom equation
(5.21),
it can be
concluded
that,
in the
case
of a
canonic
parameterization
of T, for any
scalar
function
(f>T
defined
on
DT,
the
gradient
can be
written
as
follows:
5
Induced local parameterization
on a
triangle
Let us
consider
a
discrete model
A^
2
(O,
AT,
u,Cu)
corresponding
to the
sam-
pling
of a
global
parameterization
u =
(w
1
,
u
2
)
at the
nodes
of a
triangulated
surface
T(S}.
In
this case,
an
"induced" local parameterization
(u,v)
on a
triangle
T =
T(x(a
0
),x(Q;i),x(a2))
of
T(«S)
consists
of
choosing
u and v in
such
a way
that
• u
=
u
1
linearly
interpolates
u
1
on T, and
• v
=
u
2
linearly
interpolates
u
2
on T.
According
to
equations
(6.6),
and
(6.17),
such linear interpolations
of
u
1
and
u
2
can
easily
be
deduced
from
the
barycentric
coordinates
(ub,
Vb):
4
In
this
definition,
"a x
b"
represents
the
cross product
of two
vectors,
a and b.
5
Note
that
equation
(6.22)
is, in
general,
not
true
for
other parameterizations, such
as,
for
example,
the
barycentric parameterization introduced
in the
previous section.
253

254
CHAPTER
6.
PIECE
WISE LINEAR TRIANGULATED SURFACES
This linear equation
can
also
be
written
in a
matrix
6
formulation
where
u
l
=
u
l
(ut,,Vb)
and
B
T
is the (2 x 2)
square matrix,
as
denned
by
Combining
equations (6.16)
and
equation
(6.24)
enables
us to
obtain,
finally,
an
explicit formulation
of
XT(W
I
,
u
2
):
It can be
observed
that
the
derivatives
of
XT
relative
to
u
l
and
u
2
are
identical
to
Ui
and
U^:
If
U and V
represent
the
edges
of T, as
defined
by
then
it can be
observed
that
More
about
barycentric
coordinates
on a
triangle
By
definition,
the
barycentric coordinates
of a
point
p
relative
to a
series
of
(n
+
l)
points
{
p
0
,...,
p
n
}
consist
of a set of
(n
+
1)
coefficients
{
AQ,
...,
A
n
}
such
that
If
the
points
{
p
0
,...,p
n
} are
linearly independent, then
the
coefficients
{
Ao,...,A
n
} are
unique.
In
particular, this
is the
case when
n — 2 and
6
If
this
equation
is
compared
with
equation
(5.24),
then
it can be
deduced
that
the
Jacobian
matrix
JT(U)
of the
reparameterization
defined
by
equation
(6.23)
is
such
that
J
T
(u)
=
B~
l
.

6.1.
INTRODUCTION
Figure
6.4
Barycentric coordinates
of
a
point
p in a
triangle
of
unit
area
are
related
to
some ratios
associated
with straight lines passing through
p.
{
Po'Pi'P2
I
are
^e
vertices
of a
non-degenerated triangle.
In
this case,
if
AQ,
AI,
and A2 are
denned
as
follows
then
p
appears
as
identical
to the
linear interpolation
x^(w,
v)
defined
by
equation (6.16).
Barycentric coordinates
are
invariant under
any
affine
transformation
of
the
(n
+ 2)
points
{p
;
p
0
,..
.,p
n
},
and,
in the
case
of a
triangle
T(p
0
,p
1
,p
2
),
they have
the
following
useful
properties illustrated
in figure
(6.4):
• If
triangle
T(p
0
,p
1
,p
2
)
is
subdivided into
3
subtriangles
T(p,p
1
,p
2
),
T(p
0
,p,
p
2
),
and
T'(p
0
,p
1
,p),
and if |T|
represents
the
algebraic
area
of
a
triangle
T,
then
• If two
lines passing through
p
0
and
parallel
to the
edges
J5(p
0
,p
1
)
and
-E(p
0
,p
2
)
are
drawn, then
the
intersection points
r
x
and
r
2
with these
edges
are
such
that
• If a
line passes through
p
0 and cuts the edge E(plJp2) a^ point q0,
then
Moreover,
it can
also
be
observed
that
255

256
CHAPTER
6.
PIECEWISE LINEAR TRIANGULATED SURFACES
Figure
6.5
Interpolation
of
a
function
(f>
attached
to the
nodes
of
a
triangulated
surface:
the
variations
of
</?
are
represented
by
contour lines, while
the
initial data
consist
of a set of
valuated
points
projected onto
the
surface
and
represented
by
small
cubes.
As the
contour lines
of
if>
drawn
on the
surface
show,
the
result
is
clearly
discontinuous across
the
fault
traces.
6.2
Basic
DSI
constraints
This section presents
the
most
frequently
used
DSI
constraints
for
modeling
geological
surfaces
and
their associated properties.
In
practice, these con-
straints
must
be
combined
to
integrate
the
complex
data
encountered
in the
geosciences.
6.2.1
Specifying
a
property
Fuzzy
Control-Property
As
suggested
in
figures
(4.7)
and
(6.5),
let IP be a
point located
in the
neigh-
borhood
of a
triangulated surface
T(S)
and
projected
in a
given direction
D
at
point
p on a
triangle
T =
T(x(ao),x(o:i),x(a2))
of
T(S).
The
point
IP is
assumed
to
hold
a
real value
</>(IP),
and the
linear interpolation
ipT
on T of a
property
(p
attached
to the
vertices
of
T(S]
is
required
to be
such
that
Such
a
constraint,
called
a
"fuzzy
Control-Property"
has
already
been pre-
sented
in
section
(4.7).
It is
associated with
a DSI
constraint index
c
cor-
responding
to the
above equation
(6.31),
and it
depends
on the
following
parameters:
If
(w,
v)
correspond
to a
local barycentric parameterization
of T,
then,
ac-
cording
to
equation
(4.67),
the
above constraint (6.31) generates
the
following

6.2.
BASIC
DSI
CONSTRAINTS
terms
7c(<2i)
and
T
c
(a.i\ip)
in the
local
form
of the DSI
equation
at the
vertices
(ao,Q!i,Q!2)
of T:
In
this
definition
of
jc(&i}
and
F
c
(aj((/?),
the
coefficients
Aj(p)
are
assumed
to
be the
barycentric coordinates
of p
relative
to the
three vertices
x(c^)
of T,
while
a
2
(p)
is a
normalizing factor,
as
defined
by
Fuzzy
Control-Delta
constraint
Let
(u,v)
and
(u',v')
be the
local
barycentric coordinates
of two
points
p
and
p'
located
on two
triangles
7
T and
T"
of a
triangulated surface
T(S],
respectively:
Assuming
that
(w,
v)
corresponds
to a
barycentric parameterization
of
T,
any
property
(p
defined
on the
vertices
of
T(S]
can be
linearly
interpolated
as
follows
on T and
T':
Let A be a
given value;
by
definition,
the
following
DSI
constraint
is
called
a
"fuzzy
Control-Delta constraint"
on
(p:
According
to
equation
(6.32),
such
a
constraint
is
equivalent
to
This constraint
can
easily
be
turned into
the
following
normalized
DSI
con-
straint
c =
c(w,
v,
w',
v',
T,
T",
A)
defined
by
In
practice,
these
two
triangles
are not
necessarily adjacent
and may be a
long
way
from
each other.
257
