Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.


228
CHAPTER
5.
ELEMENTS
OF
DIFFERENTIAL GEOMETRY
Figur e
5.14
Example
of
estimation
of the
curvature
vectors
along
a
regular
discrete
curve.
then
the
derivative
of
s(t) relative
to t can be
approximated
at
location
t = i
as
follows:
These approximations
in
turn allow
the
unit tangent vector
t(i)
and the
cur-
vature vector
k(i)
to be
computed
(see
figure
(5.14)):
The
Frenet
frame
and its
derivative
relative
to s can be
approximated
in a
similar
way.
Estimating
x(i)
over
an arc
E(p
i
,p
i+1
)
The
previous section
has
shown
how to
estimate
the
derivatives
x^(i)
and
Xtt(^)
at
each node
x(i)
=
p^
of a
discrete curve.
Let us now
consider
the
problem
of
approximating
x(t)
and its
derivatives over
an arc
E(p
i
^p
i+1
).
For
simplicity's sake
and
without loss
of
generality,
we can
always assume
that
i = 0.
Provided
that
E(p
i
,p
i+l
)
is
smooth enough, then
it
makes sense
to use the
following
"first
order" approximations
of
x(t)
and its
derivatives
over
E(pi,p
i+
i):
However,
bear
in
mind
that,
in
general,
x£(£)
is not the
derivative
of
x*(t)
and
x£
f
(t) is not the
derivative
of
x*
(t}.
5.5.2
Regular discrete triangulated surfaces
Let
us
consider
a
discrete
triangulated
surface
S
(e.g.,
figure
(6.1))
defined
by a
series
of
nodes
{p
0
,...,
p
M
}
and
composed
of
adjacent triangles
T(p
i:
Pj,
p
fc
).
By
definition,
such
a
discrete
surface
is
regular
if, for any
interior node
p
f
,
the two
following
conditions
are
satisfied:

5.5.
DISCRETE MODELING
229
• the
solid angle
0(p
i
]
denned
by the
triangles surrounding
PJ
is
close
to
27r,
and
• the
triangles
T(p
i5
Pj,
p
fc
)
surrounding
p
i
have, approximately,
the
same area.
In
practice, these regularity conditions
are
generally satisfied
if the
triangles
are
small enough
and the
geometry
of the
discrete surface
has
been determined
using
the
DSI
algorithm.
Continuing
to
assume
a
regular discrete
surface
leads
to the
following
problems:
• How to
estimate
numerically
the
unit normal vector
N(i)
and the
second
fundamental
tensor
L(i)
at any
node
p^.
• How to
estimate numerically
the
location
x(w,t>),
the
unit normal vector
N(w,t;),
and the
second fundamental tensor
L(u,v)
at any
point belonging
to
a
triangle
T(p
i
,p
j
,p
k
).
Estimating
the
unit
normal
vector
Nj
at
node
p^
Let
nijk
be the
(not
unit) normal vector
to a
triangle
T^
=
T(p
il
p
-,
p
fc
)
of
S:
Let us
assume
that
the
surface
S is
orientable
and
that
the
vertices
of any
triangle
T^
=
T(p
i5
p
-,
p
fc
)
of S are
sorted
in
such
a way
that
the
orientation
of
njjfc
is
compatible with
the
orientation
of S.
Under these conditions,
it is
natural
to
estimate
the
unit normal vector
N;
at
node
p^
as
where
6(z)
is the set of all the
triangles surrounding
the
node
p^.
Estimating
the
curvatures
at
node
p^
Let
us
assume
that
the
unit normal vector
N;
to S at
node
p^
is
known
and let
(U^,
Vj)
be a
given pair
of
orthonormal vectors
in the
tangent plane
Tp.(«S)
such
that
{Uj,
V^N^}
constitutes
a
right-handed
frame.
Let
X,
Y,
and Z be the
coordinates
of any
point
p of the 3D
space relative
to the
frame
{Ui.Vi.NJ:
According
to
equation (5.61),
the
osculating paraboloid tangent
to S at
node
p^
is the
graph
of a
function
Z —
f(X,
Y)
such
that
In
this
expression,
Li is the
second fundamental tensor relative
to the
canonic
reparameterization
of S
associated with
{Uj,
V^N^}:

230
CHAPTER
5.
ELEMENTS
OF
DIFFERENTIAL GEOMETRY
Using
the
components
of Li the
function
f(X,
Y)
can
also
be
written
as
fol-
lows:
The
coordinates
(X,
Y)
can be
used
for
building
a
parametric representation
x(X,
Y)
of the
paraboloid:
The
tangent vectors
xx(-X",
Y) and
xy(X,
Y) are
orthogonal
to the
unit nor-
mal
vector
N(X,
Y}
of the
paraboloid implying
that
Combining
these
two
equations with equation
(5.67),
we
conclude
that
the
following
linear system should
be
honored
for any
pair
(X,
Y):
with:
Let
N°(i)
be the set of
indices such
that
j
G
N°(i}
-4=>-
(Pj,pj)
is an
edge
of a
triangle
If
the
coordinates
of any
node
p-
relative
to
{p
i5
(U^,
V^N^)}
are
noted
as
(Xj,Yj,Zj)
and if
Nj
represents
the
associated unit normal vector, then,
according
to
equation (5.68),
we
should have:
The
least square solution
to
these linear equations
is
such
that
where
[Ai]
and Bi are a
square symmetrical matrix
and a
column matrix,
respectively,
as
defined
by

5.5. DISCRETE MODELING
231
Figure
5.15
Barycentric
approximation
on a
triangle
T(p
i
,p^p
k
).
As
soon
as the
components
of Li
have been determined thanks
to the
above
least
square equation (5.69),
it is
possible
to
compute
its
unit
eigen column
matrices
[t^^
i^]*
and
[^
t^^Y
an<
^
their associated eigen values
(&i,j,
k
2
,i)'.
Due
to the
fact
that
(U^V;)
constitutes
a new
orthonormal
frame
in the
tangent plane
Tp
(«S),
it is
known
12
that
•
{kv,i
'•
v
— 1, 2} are the
principal
curvatures
at
node
p
i5
and
• the
unit vectors
denning
the
associated principal directions
of
curvatures
ti,i
and
t2,i
at
node
p^
are
defined
by
By
performing
a
^anonic
reparameterization
of S
associated with
the
pair
(Uj
=
ti^)
and
(Vj
=
t>2,i)
so
defined,
the
second fundamental
form
relative
to
this
new
frame
is
transformed into
a new
matrix
Li
such
that
Barycentric
approximation
on a
triangle
T(p
i
,p
J
-,p
fc
)
As
suggested
in
figure
(5.15),
let p be a
given
point belonging
to a
curvilinear
triangle
T(p^,
p
-,
p
fc
)
of a
regular triangulated
surface
S,
and let
T*(p
i;
p^,
p
fc
)
be the flat
triangle interpolating linearly
the
vertices
(p^,
p
J7
p
fc
).
The
orthog-
onal
projection
p* of p on
T*(p
i5
p-,p
fc
)
can
always
be
written
as
12
See
page 213.

232
CHAPTER
5.
ELEMENTS
OF
DIFFERENTIAL GEOMETRY
where
(/3^,(3j,0k}
are the
barycentric coordinates (see page 254)
of p*
relative
to
p^,
PJ
and
p
fc
.
Provided
that
T(p
i
,p
J
-,p
fc
)
is
small
and the
surface
is
smooth enough,
the
point
p is
close
to p*. For any
(re)parameterization
x(w,
v]
of
<S,
at p,
this suggests
defining
the
"barycentric" approximation
x*(tZ,ij)
of
x(w,v)
as
follows:
Similarly,
if the
unit normal vectors
(Ni,Nj,N
fc
)
and the
second fundamen-
tal
tensors
(Li,Lj,Lfc)
are
known
at the
vertices
of
T(p
i
,p
J
-,p
fc
),
then
it is
proposed
to
define
the
barycentric approximations
N*(w,i;)
and
L*(u,
v]
as
follows:
However,
the
following must
be
noted:
• The
vector
N*(w,
v) so
denned
is, in
general,
not a
unit
vector,
meaning
that
it
should
be
replaced
by a
vector
N**(u,
t>),
as
defined
by
• The
second
fundamental
tensors
Li,
Lj,
and
Lk
at the
vertices
of
T(p
i5
p,y,
p
fe
)
have
to be
denned
in the
same
curvilinear coordinate system
(u,
v) on the
tri-
angle
T(p
i
,p
:/
-,
p
fe
).
Actually,
as
suggested
in
figure
(5.15),
these
fundamental
tensors
depend
on the
triangle
T(p
i5
p
-,
p
fe
)
and on the
pair
of
given
vectors
(U,
V)
defining
the
canonic
reparameterization
at
point
p:
The
only
difficulty
is in
evaluating
Lj,
Lj,
and
L/-.
For
example,
focusing
on
the
evaluation
of Li at
node
p^
and
thanks
to the
least
square method
presented
in a
previous section,
it is
possible
to
obtain
the
principal directions
of
curvature
ti^
and
t2,i
at
node
p^.
In
this
frame,
the
associated tensor
Li
is
then such
that
where
k\^
and
k^^
are the
associated principal curvatures.
Let us now
consider
the
"cookie
cutter"
reparameterization
(see page 209)
associated
with
the
pair
of
given
vectors
(U, V)
orthogonal
to
N*(w,
v):
According
to
equation
(5.42),
this reparameterization induces,
at
node
p
i?
a
pair
of
tangent vectors
(Ui,
V^)
defined
by
the
associated
metric
tensor
GI
is
such
that

5.6.
EXAMPLES
OF
APPLICATIONS
TO
GEOLOGY
233
Following
equations
(5.32),
and
(5.34),
the
canonic reparameterization associ-
ated
with
(Uj,
Vi)
at
node
p^
corresponds
to a
Jacobian
matrix
Jj,
as
defined
by
where
the
matrix
F^
1
is
such
that
According
to
equation
(5.27),
it can be
deduced
that
Similar
expressions
for Lj and
L^
can be
obtained,
and the
approximation
L*(u,v]
becomes:
5.6
Examples
of
applications
to
geology
5.6.1
Modeling
channels
Many
oil
reservoirs
are
composed
of
stacks
of
paleo-channels
whose geometry
controls
the
distribution
of the
porosities
and
permeabilities. Sometimes,
the
geophysics
can
capture locally
the
exact shapes
of
some
of
these channels, but,
most
of the
time,
these
shapes have
to be
simulated using
stochastic
methods.
Some
of
these stochastic methods, such
as the one
presented
on
page
531,
allow
both
well
data
and
statistical information related
to the
sinuosity
of
these channels,
but not the
direction
of the
stream,
to be
taken into account.
As
a
consequence,
the
shape
of
these
channels
may
appear
too
symmetrical.
A
method
is
proposed below
to
correct this drawback thanks
to a
postprocessing
technique
based
on the
geometry
of the
initial channel center line.
As
shown
in figure
(5.16),
let V be the
unit vector colinear
to the
global
orientation
of a
channel
and
oriented
in the
direction
of the flow, and let
(x(t)
: t G
[£05^1]}
be a
parametric representation
of the
center-line
of
this
channel. Geomorphologists have observed [214, 210]
that
the
shape
of
real
channels
is
mainly controlled
by
river bank erosion which depends
on the
local
intensity
||k(i)||
of the
center-line's curvature. This suggests introducing
a
"pseudo-erosion" vector
e(t}
defined
as a
vectorial
function
of V, k, and t:
In
this
definition
of
e(t),
the
coefficient
p(t)
is
assumed
to be a
scalar
function
with values
in the
range
[0,1]
and
modulating
the
intensity
of the
pseudo-
erosion
locally.
In
practice, stochastic simulators
(see
page
531)
used
for
generating
the
geometry
of a
channel center-line yield
a
positive
function

234
CHAPTER
5.
ELEMENTS
OF
DIFFERENTIAL GEOMETRY
Figur e
5.16
Post-processing
of
a
channel
axis
taking into
account
the
erosion
denned
by
equation
(5.75).
The
initial
axis
is
represented
by a
thin line,
while
the
result
of the
postprocessing
is
represented
by a
bold
line.
The two
grey
spots
correspond
to
locations
where
the
channel
axis
is
constrained
to
pass
and
where
the
pseudo-erosion
vanishes.
o~
2
(t)
proportional
to the
local
"uncertainty"
of
this
geometry,
13
and it may
be
wise
to
choose
p(t)
as follows:
The
vectorial
function
f(-)
occurring
in
equation (5.74) can,
of
course,
be
denned
in
many
different
ways; assuming
that
the
initial
center line
is
located
in
a
horizontal plane,
for
example,
the
vector
e(t)
can be
denned
as follows:
In the
above definition
of
e(t),
the
direction
d
a/
g
7
of the
erosion
is a
vector
defined
by
while,
for any
scalar
function
/i(t),
the
function
0(/i(t))
is
defined
as
follows:
If
the
channel
center
line
is
represented
by a
discrete
curve
(x(z)
: i =
0,
...,M},
then
it can be
transformed with
the
following
very simple algo-
rithm where
A is a
given parameter approximately equal
to the
maximum
amplitude
of the
erosion
to be
simulated:
13
For
example,
if the
simulator
is
based
on a
Kriging
method (see section
9.9.2),
then
cr
2
(t)
may
represent
the
so-called "variance
of
estimation."

5.6.
EXAMPLES
OF
APPLICATIONS
TO
GEOLOGY
235
Figure
5.17
Grey-scale display
of the
Gaussian curvature
K
of
a
triangulated
surface
and
associated directions
of
principal curvatures
ti
and
t-2.
Positive
Gaussian
curvatures
are
coded
in
light gray, while
negative
curvatures
are
coded
in
dark gray.
let v =
given number
of
iterations
let
<5
<—
A/n
for(
iter
= 0 ;
iter
< n ;
iter
+ + ) {
•
update
{k(i)
:
i =
0,...,
M}
•
compute
(e(z)
: i =
0,...,
M]
for(
i =
0
;
i<M
; i + + ) {
x(i)
•<—
x(i)
+
<5
•
e(i)
}
}
Figure
(5.16)
shows
the
effect
of
such postprocessing
on a
channel center line
obtained
by a
sequential
stochastic
simulation method described
on
page
531:
notice
that
the new
center-line
so
obtained looks like
the
center line
of a
real
channel.
In
this example,
a and
j3
were
both chosen equal
to 1,
while
7 was
chosen
equal
to 0.
5.6.2
Structural geology
Fault
detection
From
a
practical point
of
view,
at
each point
p of a
surface,
one or
several
of
the
following
parameters
can be
used
for
characterizing
the
shape
of the

236
CHAPTER
5.
ELEMENTS
OF
DIFFERENTIAL GEOMETRY
surface
in the
neighborhood
of p:
All
of
these parameters
can be
used
to
analyze
the
shape
of a
geological
surface
locally [145,
193].
Depending
on the aim of
this
analysis,
one may
choose
the
most
appropriate
parameter.
For
example:
• We
have mentioned
that
K = 0
characterizes developable surfaces, i.e.,
surfaces
that
can be
mapped onto
a
plane without
any
plastic deforma-
tion:
In
other words, this means
that
locally there
is a
direction
on the
surface
where
the
radius
of
curvature
is
infinite:
the
surface
is
locally cylindrical
and can
thus
be
locally unfolded without
any
plastic
deformation.
In a
way,
we can say
that
K
characterizes
the
"degree
of
plasticity"
of the
tectonics (see
figure
(5.17)),
and
this
is of
paramount importance
in
such
fields as
palinspastic
reconstructions
[160].
This
suggests
use of
K(p)
as an
index [145]
to
characterize
the
style
of the
tectonics
at any
point
p of a
layer according
to a
given positive threshold
KQ\
|
K(p)
\>
Ko
-4=>-
p
belongs
to a
plastic region
|
K(p)
\<
KQ
<£=>
p
belongs
to an
unfoldable
region
In
practice,
the
sign
of the
Gaussian curvature
K can
also
be
used
for
characterizing
the
shape
of the
surface
(see
figure
(5.6)):
—
If K = 0 the
surface
is,
locally,
a
plane
or a
cylindrical
fold.
—
If K > 0
then
K\
and
K2
have
the
same sign, then, locally,
the
surface
looks like
a
paraboloid.
—
If K < 0
then
K\
and
K2
have
opposite
signs,
then,
locally,
the
surface
looks like
a
hyperboloid (saddle point).
•
From
a
mechanical engineering point
of
view,
it can be
shown
(e.g.,
Sokolnikoff
[204],
pp. 198 and
212)
that,
if a
perfectly
elastic
beam
is
bent,
then
the
extension
stress
cr(p)
at a
point
p of the
beam
is
linearly
proportional
to the
curvature
ft(p) of the
beam:
This
type
of
stress
is
responsible
for the
rupture
of the
beam
as
soon
as
cr(p)
reaches
a
given
threshold
CTQ
depending solely
on the
mechanical
properties
of the
beam.
By
approximating
a
geological layer
as a
beam
and by
assuming (more
or
less) elastic behavior, every region
of the
5.6.
EXAMPLES
OF
APPLICATIONS
TO
GEOLOGY
237
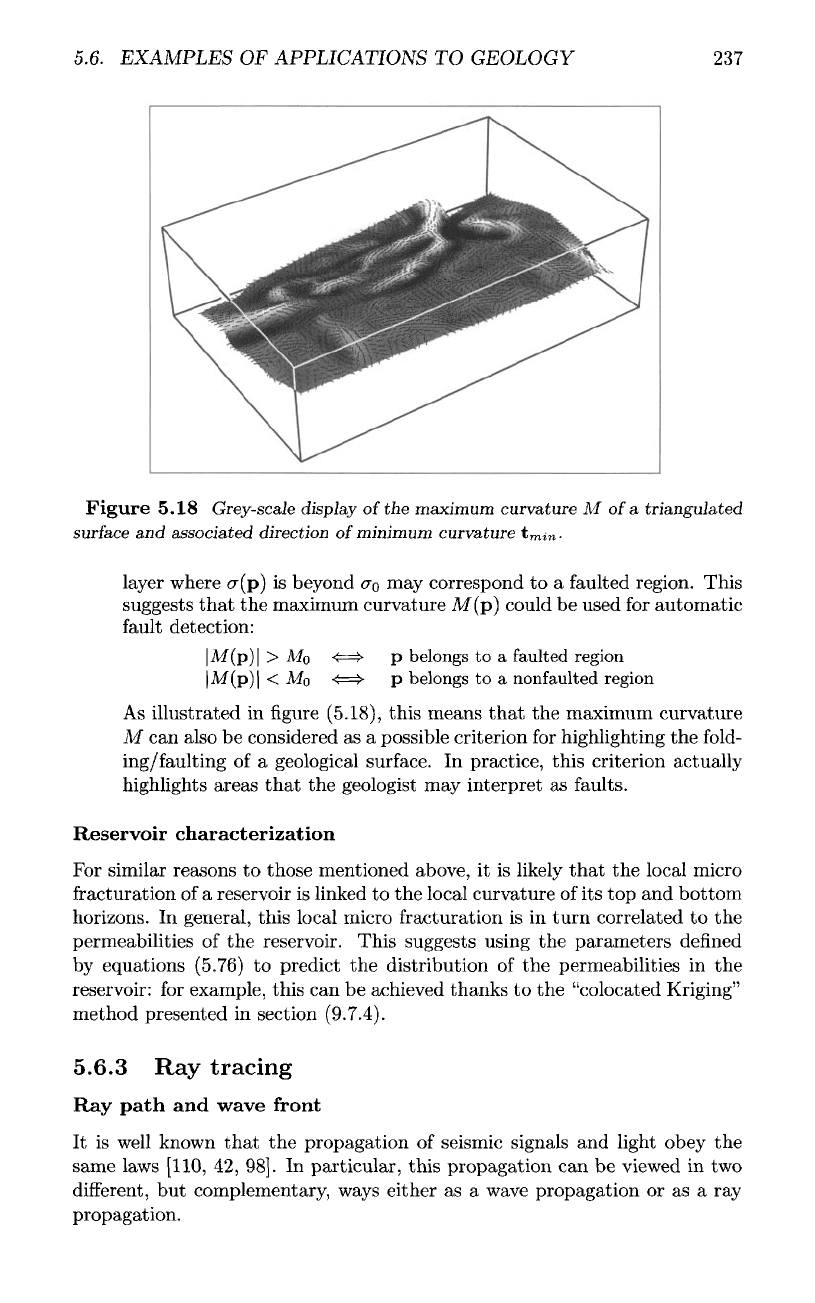
Figure
5.18
Grey-scale
display
of
the
maximum
curvature
M
of
a
triangulated
surface
and
associated
direction
of
minimum
curvature
t
m
in-
layer
where
cr(p)
is
beyond
O~Q
may
correspond
to a
faulted region. This
suggests
that
the
maximum curvature
M(p)
could
be
used
for
automatic
fault
detection:
|M(p)|
> MO
<£=>•
p
belongs
to a
faulted
region
|M(p)|
<
MO
•£=>•
p
belongs
to a
nonfaulted
region
As
illustrated
in
figure
(5.18),
this
means
that
the
maximum curvature
M can
also
be
considered
as a
possible criterion
for
highlighting
the
fold-
ing/faulting
of a
geological surface.
In
practice,
this
criterion actually
highlights
areas
that
the
geologist
may
interpret
as
faults.
Reservoir
characterization
For
similar reasons
to
those mentioned above,
it is
likely
that
the
local micro
fracturation
of a
reservoir
is
linked
to the
local curvature
of its top and
bottom
horizons.
In
general,
this
local micro fracturation
is in
turn correlated
to the
permeabilities
of the
reservoir. This suggests using
the
parameters
defined
by
equations (5.76)
to
predict
the
distribution
of the
permeabilities
in the
reservoir:
for
example, this
can be
achieved thanks
to the
"colocated
Kriging"
method presented
in
section
(9.7.4).
5.6.3
Ray
tracing
Ray
path
and
wave
front
It is
well
known
that
the
propagation
of
seismic signals
and
light obey
the
same laws [110,
42,
98].
In
particular,
this
propagation
can be
viewed
in two
different,
but
complementary, ways either
as a
wave propagation
or as a ray
propagation.
