Jean-Laurent Mallet. Geomodeling

218

CHAPTER

5.

ELEMENTS

OF

DIFFERENTIAL GEOMETRY

Figure

5.8

Examples

of

non-orientable

surfaces:

(A)

Moebius

ribbon

and (B)

Klein

bottle.

as a

linear combinations

of

x

w

and

x

v

,

and

there

is a 2 x 2

matrix

A

such

that

Multiplying

this

equation

on the

right

by the row

matrix

[x

u

,x

w

],

we

obtain

According

to

equation (5.14),

the

left-hand side

of

this equation

is

equal

to

L,

giving:

We

conclude

that

the

variations

of

the

unit normal vector

N

obey

the

following

differential

equation:

5.4

Miscellaneous

5.4.1 Orientations

and

triangulations

Orientation

of

surfaces

The

unit normal vector

N(w,

v)

always induces

the

local

orientation

of any

regular

surface

<S.

However,

this

does

not

imply

that

two

adjacent

points

p and

p'

on any

regular

surface

always have unit normal vectors

N and

N'

oriented

in the

same direction;

this

is why the

notion

of

"orientable

surface"

is

a

global

property

defined

as

follows

[61]:

A

regular

surface

S

is

called

orientable

if it can be

covered

by

a

family

of

local

parametric representations

{x(w

a

,v

a

)

: a G

A}

5.4.

MISCELLANEOUS

in

such

a way

that,

if a

point

p G

<S

belongs

to two

adjacent

neighborhoods

of

this

family,

represented

by p =

x(w

ai

,

v

ai

)

and

p =

x(w

Q2

,t;

Q2

),

then

the

determinant

det(J]

of the

associated

Jacobian

matrix

8

is

positive.

The

choice

of

such

a

family

is

called

an

orientation

of

S

and,

in

this case,

<S

is

called

oriented.

If

such

a

choice

is not

possible,

then

the

surface

is

called

non-orientable.

This definition

is

equivalent

to the one

given

on

page

68

within

the

framework

of

the

topological properties

of

manifold

objects.

For

example,

• any

surface

that

can be

covered

by a

global

curvilinear

coordinate

system

(w,

v)

is

trivially

orientable,

and

• a

Moebius

strip

or a

Klein

bottle

are

non-orientable (see

figure

(5.8)).

Fortunately, Moebius strips

and

Klein bottles

are not

"natural" surfaces

and

are

never encountered

in

geology;

in

practice,

we can

implicitly assume

that

geological

surfaces

are

always orientable.

Orientation

of a

simple

closed

curve

drawn

on a

surface

A

simple

9

closed curve

C

drawn

on an

oriented surface

S and

bounding

a

region

R C S is

said

to be

positively

oriented

if,

being located ouside

the

curve

C and

walking

on the

curve

in the

positive direction with one's head

pointing

to N, the

region

R

remains

on the

left

(see

figure

(5.9)).

Triangulation

of a

regular

region

of a

surface

Let

S be an

oriented surface.

A

region

R C S is

said

to be

regular [61]

if R

is

compact

and its

boundary

dR

consists

of a

simple closed curve.

A

triangulation

of a

regular region

R of an

oriented surface

<S

is a

cellular

partition

P(S]

of S

where

all the

2-cells

are

triangles.

Properties

of

triangulations

Surface

triangulations

have

the

following important

properties

(see [61]

p.

272):

1.

Every regular region

of a

regular surface

can be

triangulated.

2.

Let S be an

oriented surface

and

{x(w

a

,t>

Q

)

: a

<E

A}

a

family

of

local

parametric

representations

covering

S and

compatible

with

the

orien-

tation

of

<S.

For any

regular region

R C

<S,

there

is a

triangulation

T

of

R

such that every triangle

T £ T is

contained

in

some coordinate

neighborhood

of the

family

{x(w

a

,t;

a

)

: a G

A}.

Furthermore,

as

shown

in figure

(5.10),

8

See

definition

on

page

208.

9

Remember

that

a

curve

C is

said

to be

simple

if it is

piecewise regular (see definition

on

page 200).

219

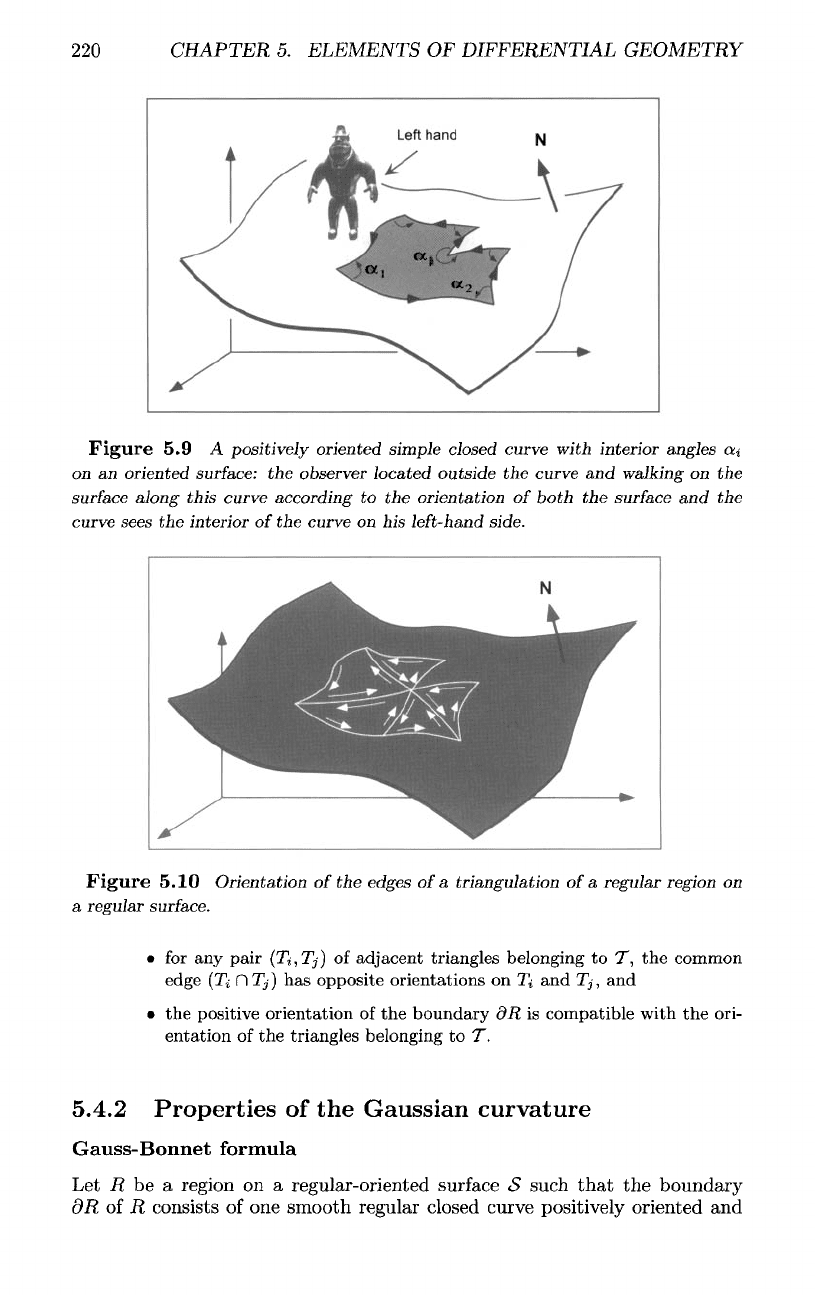
220

CHAPTER

5.

ELEMENTS

OF

DIFFERENTIAL

GEOMETRY

Figure

5.9 A

positively oriented simple

closed

curve

with

interior angles

ctj

on

an

oriented

surface:

the

observer located outside

the

curve

and

walking

on the

surface

along

this

curve according

to the

orientation

of

both

the

surface

and the

curve

sees

the

interior

of

the

curve

on his

left-hand

side.

Figure

5.10 Orientation

of the

edges

of

a

triangulation

of

a

regular region

on

a

regular

surface.

• for any

pair

(Ti,Tj)

of

adjacent

triangles

belonging

to T, the

common

edge

(Ti

D

Tj)

has

opposite orientations

on Ti and

Tj,

and

• the

positive orientation

of the

boundary

dR is

compatible with

the

ori-

entation

of the

triangles

belonging

to

T.

5.4.2

Properties

of the

Gaussian

curvature

Gauss-Bonnet

formula

Let

R be a

region

on a

regular-oriented

surface

S

such

that

the

boundary

dR of R

consists

of one

smooth

regular

closed

curve

positively

oriented

and

5.4.

MISCELLANEOUS

2

having

a

geodesic curvature equal

to

k

5

.

Then,

the

Gauss-Bonnet

formula

states

that

we

have

where

t is the

unit tangent

to dR,

while

s is the

curvilinear abscissa

of

OR

and da is the

element

of

area

of R.

For

example,

• If R is a

disc

in the

plane,

then

we

have

0 +

2?r

=

2?r.

• If R is the

upper

part

of the

unit

sphere,

then

we

have

2?r

+ 0 =

27T.

As

shown

in figure

(5.9),

if the

boundary

dR is

piecewise regular with inte-

rior

angles

c^,

then

the

Gauss-Bonnet

formula

takes

a

slightly

different

form,

including

the

contribution

X^(TT

—

on}

of the

corners

of dR:

In

particular,

if R — A is a

geodesic triangle bounded

by

three geodesic edges,

then

we

have:

For

example,

if S is a

sphere with

a

radius

equal

to r and A a

geodesic triangle

having

an

area equal

to

A,

then

we

obtain

Characterizing

developable

surfaces

A

regular

surface

S is

said

to be

"developable"

if it is

possible

to

unfold

it on

a

plane without

any

shearing

or

plastic

deformation.

In

other words, after

unfolding,

• the

length

of

curves drawn

on a

developable

surface

are

preserved,

• the

value

of

angles

drawn

on a

developable

surface

are

preserved,

and

• the

areas

of

regions drawn

on a

developable

surface

are

preserved.

It can be

shown [61]

that

a

regular surface

S is

developable

if, and

only

if, its

Gaussian curvature vanishes everywhere:

{S

is

developable

}

Relative

developability-index

As

discussed above,

at

each point

p of a

surface

S, the

Gaussian curvature

K

characterizes

the

aptitude

of the

neighborhood

of p to be

unfolded

on a

plane.

It

should

be

noted, however,

that

the

actual value

of K

depends

on the

units

used

to

measure

the

lengths

on

<S.

In the

context

of

some applications

(e.g.,

see

page

293),

it may be

useful

to

look

for a

dimensionless index characterizing,

in

an

equivalent way,

the

possibility

to

unfold

«S,

locally.

For

this purpose,

we

221

222

CHAPTER

5.

ELEMENTS

OF

DIFFERENTIAL GEOMETRY

Figur e

5.11

Osculating

paraboloid

and

associated

Dupin

indicatrix

at a

point

p of a

regular

surface.

suggest using

the

"relative

developability-index"

Dev

defined

as

follows

where

m

\K\/s

is

the

mean value

of \K\

computed

on

S:

In

this

definition,

e

is

assumed

to be a

very small positive number whose only

purpose

is to

ensure

that

Dev =

I

everywhere when

K = 0

everywhere. Note

that

Dev

belongs

to the

range

[0,1]

and Dev — 1/2 if \K\

=

m\K\/s-

5.4.3

Osculating paraboloid

Definition

Let

(U,

V) be a

pair

of

orthogonal unit vectors

in the

tangent plane

Tp(<5)

such

that

(U, V, N)

constitutes

a

direct orthogonal trihedron attached

to p

=

Tp(<S).

Using

the

Taylor series expansion

formula

(see 147),

the

orthonormal

canonic

reparameterization

x(w,

v)

associated with

(U, V) is

such

that

We

can

observe

that

x^

= U, and

this implies

that

Similarly,

we can

show

that

5.4.

MISCELLANEOUS

223

Using

these relationships,

if we

project

the

increment

Ax on the

local

frame

(U, V, N), we

obtain

In

other words, within

the

framework

(U, V, N),

locally

<S

is the

graph

of a

function

Z —

f(X,

Y)

such

that

This

function

represents

a

paraboloid tangent

to S at

point

p and

called

"osculating

paraboloid"

(see

figure

(5.11)).

Dupin

indicatrix

Let

p be a

point

in

<5.

The

Dupin indicatrix

at p is the set of

vectors

W of

the

tangent plane

Tp(«S)

such

that

To

write

the

Dupin indicatrix

in a

more convenient

form,

it is

always possible

to

choose

U and V

identical

to the

principal directions

of

curvature

ti

and

t-2

at

point

p:

In

this case,

the

matrix

L

becomes diagonal,

and its

diagonal elements

are

identical

to the

principal curvatures

k\

and

k^:

Thus,

the

coordinates

(X,Y)

of a

point

of the

Dupin

indicatrix

satisfy

the

equation:

In

other words,

the

Dupin indicatrix

is a

union

of

conies

in

Tp(<S)

and

this

suggests saying

that

10

• p is an

elliptic

point

if the

Dupin

indicatrix

is an

ellipse,

that

is to

say,

if

ki

and

k-2

are

different from

zero

and

have

the

same

sign.

• p is a

hyperbolic

point

if the

Dupin

indicatrix

is

made

of a

hyperbola

with

common

asymptotic

lines.

This

occurs

if

k\

and

ki

are

different from

zero

and

have

different

signs.

• p is an

umbilical

point

if the

Dupin

indicatrix

is a

circle,

that

is to

say,

if k\

and

&2

are

different from

zero

and are

equal.

• p is a

parabolic

point

if the

Dupin

indicatrix

degenerates

into

a

pair

of

parallel

lines,

that

is to

say,

if k\ or

ki

is

equal

to

zero.

10

See

figures

(5.11),

and

(5.6).

223

224

CHAPTER

5.

ELEMENTS

OF

DIFFERENTIAL GEOMETRY

Figure

5.12

Composite

G

1

curves

and

surfaces

composed

of

two

adjacent

pieces.

Note

that

the

composite curve

is

composed

of two

tangent circles

with

a

different

curvature.

5.4.4 Geometric continuity

In CAD

applications, most

of the

time ones uses composite curves

and

sur-

faces.

As

shown

in figure

(5.12):

• a

composite curve

is a set of

adjacent pieces

of

C

n

regular parametric curves,

and

• a

composite surface

is a

patchwork composed

of

adjacent pieces

of

C

n

regular

parametric surfaces.

The

problem

of

continuity arises

at the

junctions

of

these pieces

of

curves

and

surfaces.

The

classic notions

of

C

n

-continuity

requires using

one

single

parametric space

for all

these pieces. This

is

very inconvenient

and

often

impossible

to

realize

in

practical

applications.

Therefore,

a new

type

of

char-

acterization

of the

continuity called

"

Geometric

Continuity

1

'

1

and

abbreviated

"G

n

continuity"

has

been introduced.

As

will

be

seen

in the

paragraphs,

the

idea

of

geometric continuity

involves

only geometric notions such

as

points, tangents,

and

curvatures

and

can

thus

be

used even

if the

different

elements

of the

composite curves

and

surfaces

are

based

on

different

parametric spaces.

G

n

continuity

of

curves

Let

C be a

composite curve consisting

of a set of

adjacent parametric curves

{Ci,...,

C

n

},

each

of

them having

a

C

n

-continuity

on

their parametric domain.

The

G

n

continuity

of

such

a

patchwork

for n =

(0,1,2)

is

denned

as

follows:

• C is

G°

continuous

if the

following

condition

is

respected:

—

for any

pair

of

adjacent curves

(Ci,

Cj)

belonging

to C,

there

is no gap at

their

common point

Pij.

• C is

G

l

continuous

if C is

already

G°continuous

and the

additional fol-

lowing

conditions

are

respected:

5.4.

MISCELLANEOUS

—

the

equation

Xi(£)

of any

curve

d

belonging

to C is

regular.

—

any

pair

of

adjacent curves

(d,Cj)

belonging

to C

share

a

common tan-

gent

at

their common point

Pij.

• C is G

2

continuous

if C is

already

G

1

continuous

and the

additional

following

condition

is

respected:

—

any

pair

of

adjacent curves

(d,Cj)

belonging

to C

share

a

common

os-

culating circle

at

their common point

Pij.

G

n

continuity

of

surfaces

Let

<S

be a

patchwork

consisting

of a set of

adjacent

parametric

surfaces

{Si,...,

S

n

},

each

of

them

having

a

C

n

continuity

on

their

parametric

domain.

The

G

n

continuity

of

such

a

patchwork

for

n

=

(0,1,

2) is

defined

as

follows:

•

<S

is

G°

continuous

if the

following

condition

is

respected:

—

for any

pair

of

adjacent patches

(Si,Sj)

belonging

to

<S,

there

is no gap

along their common edge

Eij.

• S is

G

1

continuous

if S is

already

G°

continuous

and the

additional

following

conditions

are

respected:

—

the

equation

Xi(w,

v)

of any

patch

Si

belonging

to S is

regular.

—

any

pair

of

adjacent patches

(«Si,«Sj)

belonging

to

«S,

share

a

common

tangent plane along their common edge

Eij.

• S is

G

2

continuous

if S is

already

G

1

continuous

and the

additional

following

condition

is

respected:

—

any

pair

of

adjacent patches

(Si,Sj)

belonging

to S

share

a

common

osculating paraboloid along their common edge

Eij.

3-Tangents

theorem

The

definition

of the

notion

of

G

2

continuity

of

surfaces

is

somewhat

inconve-

nient

in

practical

applications

and,

for

this

reason,

equivalent

conditions

have

been

proposed

in the

literature.

For

example,

Pegna

and

Wolter

[172]

have

proposed

the

following

straightforward

11

u

3-Tangents

theorem:"

Any

pair

(«Si,«Sj)

of

adjacent

G

1

continuous patches belonging

to S are

G

2

continuous

if, for any

point

x

belonging

to the

common

edge

Eij,

they share

a

common normal curvature

fc

n

(x, ti) at

least

in 3

tangent

directions

ti =

(ti,t2,t3).

11

The

osculating paraboloid depends

on L,

which,

in

general,

has

three

independent

components.

These

three

components

can be

determined

as a

function

of the

curvatures

in

three

independent directions.

225

226

CHAPTER

5.

ELEMENTS

OF

DIFFERENTIAL GEOMETRY

Figur e

5.13

Parameterizing

a

discrete

curve.

5.5

Discrete

modeling

In

practice,

if a

discrete approach

is

used

for

modeling curves

and

surfaces (see

chapter

1),

these geometric objects

are

denned

by

ID

and 2D

graphs

£7(0,

N)

whose

nodes

{PI,PI,

• •

-,PM)

nave

given locations

in the 3D

space:

• In the

case

of a

discrete

curve,

the

graph

C?(f2,

N)

can be

decomposed

into

a

series

of

adjacent

arcs

E(p

i

,p

i+l

).

• In the

case

of a

discrete

surface,

the

graph

C?(f2,

AT)

can be

decomposed into

a set of

adjacent

triangles

T(p

i

,

Pj,p

k

),

rectangles

R(p^

Pj,p

k

,

p/J,

or,

more

generally,

polygons.

The

parametric equations

of

these arcs, triangles,

or

rectangles

are

unknown,

and the

only information available

is the

location

of

their vertices. Prom this

limited information,

it is

possible

to

build complex parametric regular curves

and

surfaces. Chapter

7

describes

how

this goal

can be

achieved.

These

parametric models

are

based

on

algebraic equations,

and all the

derivatives

used

in

differential

geometry

can

easily

be

computed.

This section will show

that

these derivatives

and

differential

properties

can

be

approximated directly using

finite

differences

without having

to

build such

complex algebraic models.

5.5.1

Consider

a

discrete curve

defined

by a

series

of

nodes

(p

0

,...,

PM}-

As

SU

S~

gested

in figure

(5.13),

it

will

be

assumed

that

the

regular (unknown) curve

interpolating these nodes

is

represented

by an

unknown parameterization

x(i)

such

that

By

definition, such

a

discrete

curve

is

said

to be

regular

if the two

following

conditions

are

satisfied

for any

node

p^:

• the

angle

9(p

i

)

between

(Pi_i

—

pj

and

(p

i+1

—

pj

is

close

to

TT,

and

• the

segments

(p

i+1

—

Pj)

have,

at

least

locally,

approximately

the

same

length.

In

practice, these regularity conditions

are

generally satisfied

if the

arcs

are

small enough

and the

geometry

of the

discrete curve

has

been determined

using

the

DSI

algorithm.

Regular discrete curves

5.5. DISCRETE MODELING

227

Assuming

a

regular discrete curve leads

to the

following

problems:

• How to

estimate numerically

the

derivatives

xt(z),

x«(i)

and the

associated

geometric

entities

at

node

p^.

• How to

estimate

numerically

the

location

x(i)

and the

derivatives

xt(t)

and

xtt(i)

on any arc

^(p^p^J.

Estimating

the

derivatives

of

x(£)

at

location

t

=

i

Any

scalar

function

</?(£)

defined

by its

values

{(p(i)

:

i = 0,

...,M}

at the

nodes

of a

regular discrete curve

can be

approximated locally

in a

least

square

sense

by a

polynomial

of

degree

n in a

neighborhood

[i — N, i +

N]

of t = i

where

TV

is a

given positive integer:

For

example,

if N = 3, in the

case

of a

polynomial

of

degree

n = 2

approxi-

mated

on (2N + 1)

=

7

nodes centered

on

p

{

,

the

coefficients

{a^(<£>)}

can be

determined

as

follows

from

the

sampled values

of

</?

(see

[145]):

By

derivation

of

equation

(5.64),

these

coefficients

allow

the

derivatives

of any

scalar

function

(p(t)

at

location

t = i to be

approximated:

Due

to the

least square approximation,

the

evaluation

of the

derivatives

so

defined

is, in

general, numerically stable

and can be

used

to

compute local

differential

properties

geometry

of the

discrete

curve

at

location

t = i. For

example,

if

(p

is

identified

with

the

components

of

x(t),

then

x

t

(i)

and

Xft(z)

can be

approximated

by

Similarly,

if

(p(t]

represents

the arc

length

s(t]

as

defined

by

Jean-Laurent Mallet. Geomodeling

Подождите немного. Документ загружается.