Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.


278
CHAPTER
6.
PIECE
WISE
LINEAR TRIANGULATED SURFACES
By
definition, such
a
constraint
is
called
a
"Boundary-on-Surface"
constraint
and is
implemented
as a
hard
DSI
constraint (see section
(4.5)),
which consists
of
projecting each node
a €
f3(S/F]
on
F
in a
given direction
d(a)
at
each
step
of the
iterative
DSI
algorithm.
In
practice,
the
projection directions
associated
with
the
nodes
{a
G
^(S/F}}
are
denned
as
follows:
•
each
direction
d(a)
is
initialized
to be
colinear
to the
straight
line
joining
x(a)
to its
closest
point
on the
fault
0-\
•
next,
the
directions
(d(a)
: a £
(3(S/J-}}
are
smoothed
by
applying
the DSI
algorithm
on a
discrete
model
M^(B,
NB,
d,Cj)
where
B
consists
of all the
nodes
of
/3(S/.F).
The
Boundary-on-Surface constraint
DSI can
then easily
be
implemented
as
a
series
of
fuzzy
Control-Distance constraints (see page 168)
specifying
that
each node
{a
€
^(S/F)}
should
be
located
at a
null
distance
from
the
target
J-
in the
direction
d(a).
Figure (6.34) shows
the
effect
of a
Boundary-on-Surface constraint when
the
shape
of a
horizon
is
edited interactively
in the
neighborhood
of a
fault
trace.
Boundary-Stone-on-Boundary
constraint
When considering
a
fault
J-"
partly
cutting
a
geological surface
<S
along
a
fault
trace
B(S/f}
(see
figure
(6.34)),
the
twin boundaries
P(S/F)
and
P'(S/F)
may
share
a
common point
/3*(<S/.F)
located
on the
boundary
of
T
called
a
"Boundary Stone."
If the
geometry
of S is
modified,
then
the
Boundary
Stone
f3*(S/J
:
}
has to
slide along
the
boundary
of
T.
For
this purpose,
a
"Boundary-Stone-on-Boundary"
DSI
constraint
defined
as
follows
should
be
installed
for
each Boundary Stone
j3*(S/f):
• first, a
direction
d(/3*)
is
determined
as
being
colinear
to the
straight
line
joining
x(/3*)
to its
closest
point
on the
boundary
of the
fault
F\
• the
Boundary-Stone-on-Boundary
constraint
is
then
implemented
as a
fuzzy
Control-Distance
constraint (see page 168)
specifying
that each node
j3*
should
be
located
at a
null
distance
from
the
boundary
of
J-
in the
direction
d(a).
Figure (6.34) shows
the
effect
of a
Boundary-Stone-on-Boundary
constraint
when
the
shape
of a
horizon
is
edited interactively
in the
neighborhood
of a
fault
trace.
6.4
Continuity
through
faults
Let
(^(H,
v) be a
scalar function
defined
on the
same
parametric domain
D
as a
parameterization
x(u,
v) of a
surface
S:
By
definition
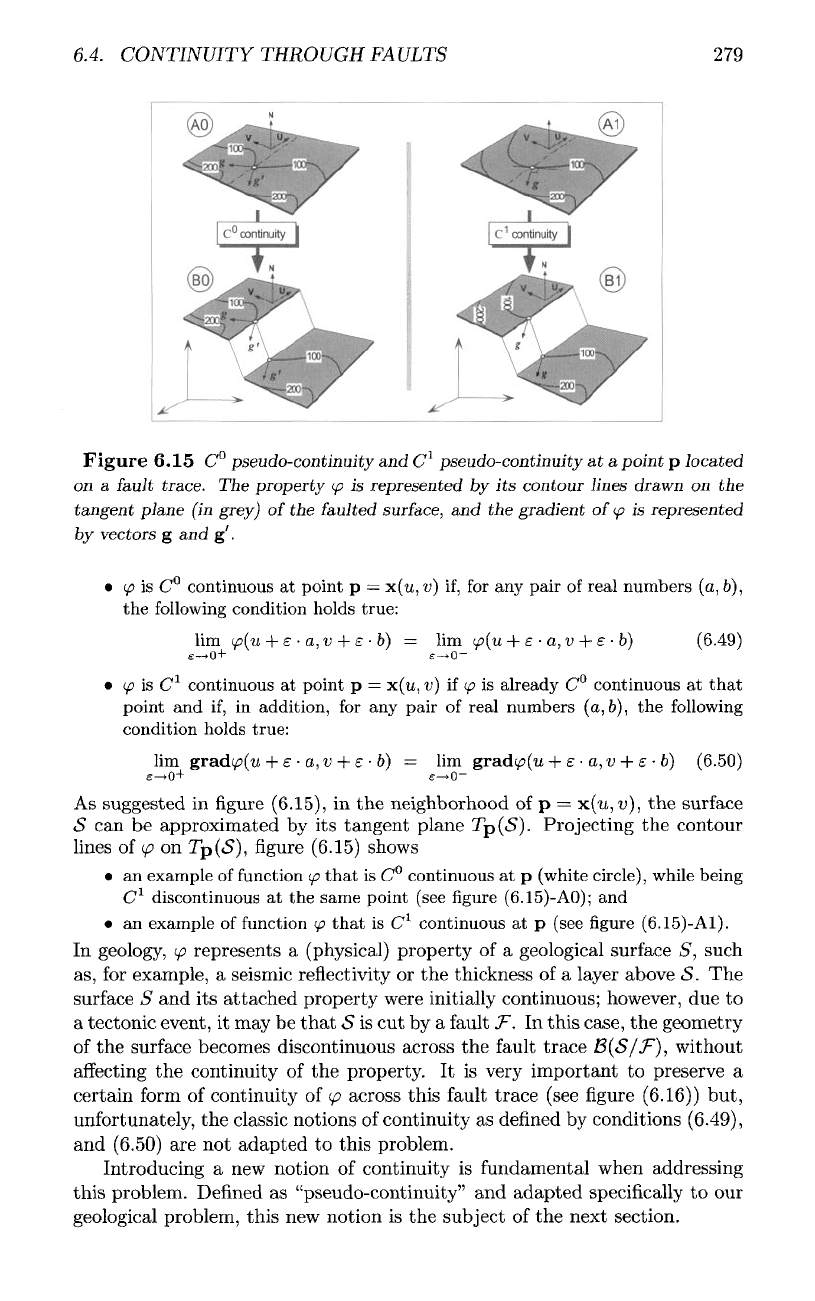
6.4. CONTINUITY THROUGH FAULTS
279
Figure
6.15
C°
pseudo-continuity
and
C
1
pseudo-continuity
at a
point
p
located
on a
fault
trace.
The
property
(p
is
represented
by its
contour
lines
drawn
on the
tangent
plane
(in
grey)
of the
faulted
surface,
and the
gradient
of
y>
is
represented
by
vectors
g and
g'.
•
ip
is
C°
continuous
at
point
p
=
x(w,
v) if, for any
pair
of
real numbers
(a,
b),
the
following
condition
holds
true:
•
(p
is
C
l
continuous
at
point
p —
x(u,
v) if
if>
is
already
C°
continuous
at
that
point
and if, in
addition,
for any
pair
of
real
numbers
(a,
6),
the
following
condition
holds
true:
As
suggested
in
figure (6.15),
in the
neighborhood
of p =
x(u,
v), the
surface
<S
can be
approximated
by its
tangent
plane
Tp(«S).
Projecting
the
contour
lines
of
</?
on
Tp(«S),
figure
(6.15) shows
• an
example
of
function
(f>
that
is
C°
continuous
at p
(white
circle),
while
being
C
1
discontinuous
at the
same point (see
figure
(6.15)-AO);
and
• an
example
of
function
(p
that
is
C
1
continuous
at p
(see
figure
(6.15)-A1).
In
geology,
(p
represents
a
(physical) property
of a
geological surface
5,
such
as,
for
example,
a
seismic reflectivity
or the
thickness
of a
layer
above
S. The
surface
S and its
attached
property were initially continuous; however,
due to
a
tectonic
event,
it may be
that
S is cut by a
fault
J-.
In
this
case,
the
geometry
of
the
surface becomes discontinuous across
the
fault
trace
B(S/F],
without
affecting
the
continuity
of the
property.
It is
very important
to
preserve
a
certain
form
of
continuity
of
</?
across
this
fault
trace
(see
figure
(6.16))
but,
unfortunately,
the
classic notions
of
continuity
as
defined
by
conditions (6.49),
and
(6.50)
are not
adapted
to
this
problem.
Introducing
a new
notion
of
continuity
is
fundamental when addressing
this
problem.
Defined
as
"pseudo-continuity"
and
adapted
specifically
to our
geological problem,
this
new
notion
is the
subject
of the
next
section.

280
CHAPTER
6.
PIECEWISE LINEAR TRIANGULATED SURFACES
Figure
6.16
Pseudo-continuity
associated
with
Vectorial-Links.
6.4.1
Pseudo-continuity
across
a
fault
Definition
As
shown
in
figures
(6.15)-AO
and
(6.15)-A1,
let (U, V) be the
frame
located
in
the
tangent
plane
Tp(«S)
at
point
15
p
=
x(u,
v)
on the
surface
<S,
as
defined
by
This
surface
is
assumed
to be cut by a
fault
F
passing through
p
along
a
fault
trace
16
B(S/J-~).
After
cutting
<S
by the
fault,
the
initial tangent plane
is
also
cut
into twin
parts.
One of
these
parts
is
affected
by a
(relative) rigid
displacement
T>
transforming
p and its
associated
frame
(U, V)
into
a
twin
point
p'
and an
associated twin
frame
(U',
V'):
Let us now
consider
a
function
(p
defined
on
<S,
and let
grad<£>|p
and
grad<p|p/
be the
gradient
of
(p
computed
on
both
sides
of the
fault
at the
twin
points
p
and
p'.
Taking into account equations (6.51)
and
(6.12),
it can be
observed
that
By
definition,
•
(p
is
C°
pseudo-continuous
across
the
fault
trace
if
</?
has the
same value
at
points
p and
p':
15
Point
p =
x(u,
v)
is
represented
by a
white
circle
in figure
(6.15).
16
The
fault
trace
is
represented
by a
dashed line
in figures
(6.15)-AO
and
(6.15)-Al.
For
simplicity's
sake,
in
this
figure the
fault
trace
is
drawn parallel
to U, but
this
is not at all
mandatory.

6.4.
CONTINUITY THROUGH
FAULTS
•
(p
is
C
l
pseudo-continuous across
the
fault
trace
if
(p
is
already
C°
pseudo-
continuous
and if, in
addition,
the
gradient
at
p'
is
deduced
from
the
same
rigid
displacement
as the one
introduced
in
equation (6.51):
As
suggested
in
figure
(6.15),
in the
neighborhood
of p and
p',
the
surface
<S
can be
approximated
by its
tangent planes
Tp(«S)
and
Tp>(<5).
If the
contour
lines
of
(p
are
projected onto these tangent planes,
then
figure
(6.15) shows:
• an
example
of the
function
(p
that
is
C°
pseudo-continuous
at p
(white circle),
while being
C
l
pseudo-discontinuous
at the
same
point
(see
figure
(6.15)-BO),
and
• an
example
of the
function
(p
that
is
C
1
pseudo-continuous
at p
(see
figure
(6.15)-B1).
The
case
of a
triangulated
surface
In
practice,
as
shown
in
figures
(6.13),
and
(6.17),
it is
assumed
that
the
faulted
surface
S is
modeled
as a
triangulated
surface
T(«S)
whose nodes
a 6 0
have
a
given
location
x(o:)
in the 3D
space. Referring
to the
notations
introduced
in
section
(6.3.2)
and
illustrated
in
figure
(6.13),
we see
that
the
displacement
V at
P(s^)
is
defined
by the
vector
(P(sf)
—
P'(si)}:
As
suggested
in
figures
(6.16),
and
(6.17),
in the
next
two
sections
T =
T(x(a
0
),x(ai),x(a2))
and
T'
=
T(x(a
f
0
),x(a'
l
),x(a'
2
})
will
represent
the
twin
triangles
of
S
whose edges
.E(x(a:o),x(a:i))
and
E(x.(aQ},x(a())
contain
P(SJ)
and
P'(SJ),
respectively:
6.4.2
Preserving
a
C°
pseudo-continuity
Considering
the
twin points
P(SJ)
and
P'(si)
in figure
(6.13),
let
{«»,(!
—
Ui)}
and
{u^
(1
—
i^)}
be the
barycentric coordinates (see page 254)
of
these
two
points relative
to
{x(ao),x(o;i)}
and
(x(o;o),x(a
/
1
)}.
Thanks
to
these
barycentric coordinates,
the
linear interpolation
<f)(si)
and
</>'(si)
of
(p
at
P(fii)
and
P'(SZ)
can be
expressed
as
follows:
According
to our
definition
in
equation (6.52)
of the
C°
pseudo-continuity
at
(P(sj),P'(si)},
the
following
constraint must
be
respected:
Let
c be the
DSI
constraint
that
depends
on the following
parameters
c
=
c(i,
Wi,i4,0!o,ai,a:o,a:'i)
281

282
CHAPTER
6.
PIECEWISE LINEAR TRIANGULATED SURFACES
and
defined
by
where
a
c
is a
normalizing factor chosen
as
follows
so
that
\\A
C
\\
= 1:
Define
O
c
((p]
as
follows:
When added
to the set of
constraints
C^
of the
discrete model
A4
*
(fi,
TV,
</?,£<£),
the
above constraint induces
the
following
terms
7
c
(ct)
and
T
c
(a\(f>]
at
nodes
a
=
ao
and
a —
a\
in the
local
form of the
DSI
equation:
Similar
terms
7
c
(a)
and
T
c
(a\(f>)
are
induced
17
at
nodes
a =
a'
0
and a =
a[:
6.4.3
Preserving
a
C
l
pseudo-continuity
For
simplicity's sake,
as
suggested
in
figure
(6.17),
let us
assume
that
the two
twin
triangles
are
represented
by
local
canonic
parameterizations introduced
in
section (6.1.3), respectively. According
to
equation
(6.22),
this
implies
that
the
linear interpolations
({>T
and
<PT>
of
(p
on T and
T"
are
such
that
17
Pay
attention
to the
signs
'+' and
'—',
which
may
have changed.

6.4.
CONTINUITY THROUGH
FAULTS
Figur e
6.17
Twin
triangles
involved
in the
pseudo-continuity
at
twin points
{P(si),
P'(SJ)}.
These
triangles
are
assumed
to be
represented
by
canonic
parame-
terization
such
that
(U, V) is
transformed
into
(U',
—V)
after
displacement
due to
a
tectonic
event.
Referring
to
figure
(6.17),
in
this particular case,
the
rigid displacement
T>
corresponding to the throw (P'(si) — P(si)} ig sucn that18
According
to
equations
(6.53),
(6.55),
and
(6.56),
the
following
constraint
is
equivalent
to
According
to
equation (6.9), these
two
constraints
are in
turn equivalent
to
the
following
pair
of
constraints where
the
coefficients
{A
M
,
A
v
}
defined
by
equation
(6.8)
depend only
on the
geometry
of the
triangles
T and
T":
These linear constraints
can
easily
be
turned into
a
pair
of
DSI
constraints
c
u
=
c
u
(i,ao,ai,a2,a'
Q
,a'
l
,a'
2
)
and
c
v
=
c
v
(i,ao,
o?i,
0:2,
ct^a^a^)
defined
18
Pay
attention
to the
"-"
sign
induced
by the
opposite
orientations
of the
frames
(U, V)
and
(U',
V) on the
triangles
T and
T'.
283

284
CHAPTER
6.
PIECEWISE LINEAR TRIANGULATED SURFACES
by
and
In
the
above
definition
of the
constraints
{c*
: *
=
u or
i;)},
the
coefficients
{A
c
*(a)}
are all
assumed
to be
equal
to
zero except when
a is
equal
to
ao,
Q!I,
ct2
or
O!Q,
a^,
a'
2
.
Futhermore,
the
coefficient
a
c
*
is a
normalizing factor
(see
equation
(4.4))
chosen
as
follows
to
guarantee
that
||-A
C
*||
= 1:
Define
0
C
*
(if)
as
follows:
When added
to the set of
constraints
C
v
of the
discrete model
A4
1
(O,
AT,
</?,
C^),
the
twin constraints
(6.57),
and
(6.58) induce
the
following
terms
7
c
*(oO
and
F
c
*(o;|(/?)
in the
local
form
of the
DSI
equation:
6.4.4
A
test
example
This section presents
an
actual example showing
how to
model
the
geometry
x
and a
property
(p
of a
faulted triangulated surface T(S) with
the DSI
method.
In
this
example,
it is
assumed
that
a
draft model
of the
geometry
has
been
obtained,
and the
geologist would like
to
•
edit
the
fault-throw
vectors interactively,
and
•
interpolate
a
property
(f
continuously
on
T(S)
.
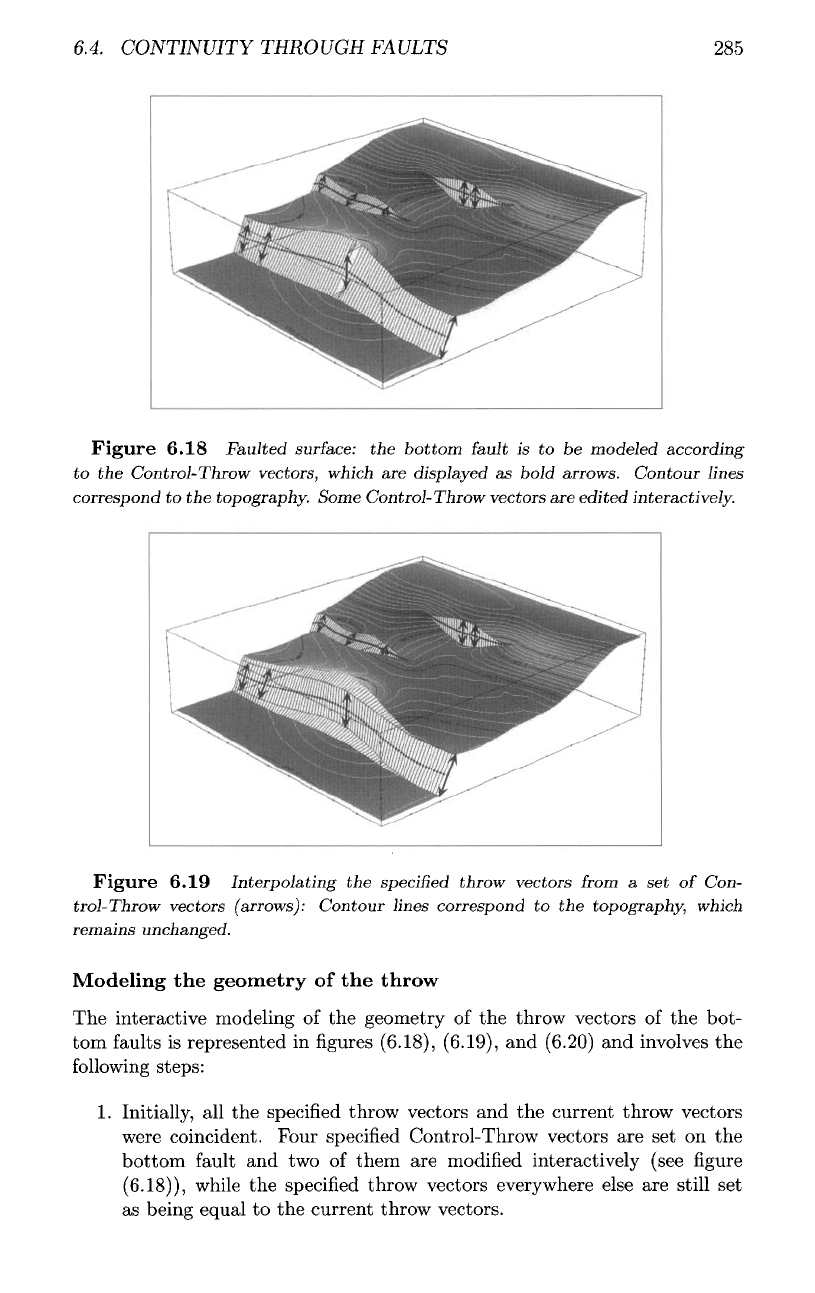
6.4.
CONTINUITY THROUGH
FAULTS
Figur e
6.18
Faulted
surface:
the
bottom
fault
is to be
modeled according
to the
Control-Throw vectors, which
are
displayed
as
bold
arrows. Contour lines
correspond
to the
topography. Some Control-Throw vectors
are
edited interactively.
Figure
6.19
Interpolating
the
specified
throw vectors
from
a set of
Con-
trol-Throw vectors
(arrows):
Contour lines correspond
to the
topography, which
remains unchanged.
Modeling
the
geometry
of the
throw
The
interactive modeling
of the
geometry
of the
throw vectors
of the
bot-
tom
faults
is
represented
in
figures
(6.18),
(6.19),
and
(6.20)
and
involves
the
following
steps:
1.
Initially,
all the
specified
throw vectors
and the
current throw vectors
were
coincident. Four
specified
Control-Throw vectors
are set on the
bottom
fault
and two of
them
are
modified
interactively (see
figure
(6.18)),
while
the
specified
throw vectors everywhere else
are
still
set
as
being equal
to the
current throw vectors.
285

286
CHAPTER
6.
PIECEWISE LINEAR TRIANGULATED SURFACES
Figure
6.20
Taking
into
account
the
specified
throw
vector
constraints
for in-
terpolating
the
geometry
of
the
surface:
contour
lines
correspond
to the
topography,
which
is
modified.
Note that
the
specified
throw
vectors
are now
honored.
2.
The
next step consists
in
smoothly interpolating
the
specified
throw
vectors
of the
bottom fault
by
applying
the
DSI
algorithm
to the
discrete
model
A^
3
(A,
A^A,T,C
T
).
The
result
of
this
interpolation
is
shown
in
figure
(6.19), where
it can be
seen
that
• the
specified
Control-Throw
vectors
{r(€)
:
I
G
LA}
are
kept
unchanged;
• the
specified
throw
vectors
{r(6i)
:
6i
(E
A}
are now
different
from
the
current
throw
vectors
T(SJ).
3.
The final
step involves applying
the DSI
algorithm
to the
discrete model
.M
3
(O,
TV,
x,
Cx)
associated with
the
surface
S to
honor
the new set of
specified
throw vectors smoothly.
As can be
seen
in figure
(6.20),
after
applying
DSI,
the
surface
S
does honor
all the
specified
throw vectors.
In
practice,
if the
geometry
of the
faults cutting
the
surface
is
known,
it
is
wise
to add the
associated Boundary-on-Surface constraints
to
Cx
(see
section
(6.3.2)).
Modeling
the
properties
Figures
(6.5),
and
(6.21)
show
the
application
of DSI
constraints
to
restore
the
continuity
for
physical property modeling across
the
faults. Figure (6.5) shows
the
result
of
using
the
faulted surface
as a
topological basis
for
interpolation
without
setting
the
C°
and
C
l
pseudo-continuity
DSI
constraints across
the
faults:
the
property modeled here
is
clearly discontinuous. Figure
(6.21)
shows
the
result obtained with
the
same data,
but
using
the
C°
and
C
l
pseudo-
continuity
DSI
constraints
to
restore
the
continuity
of the
property across
the
fault:
the
contour lines
of the
property
are now
continuous across
the
faults.

6.5.
GLOBAL PARAMETERIZATION
Figur e
6.21
Interpolating
a
physical
property
on a
faulted
surface
with
restora-
tion
of the
continuity
thanks
to
C°
and
C
l
DSI
constraints:
contour
lines
of the
property
are
continuous
across
the
fault
traces
(compare
with
figure
(6.5)).
6.5
Global
parameterization
As
illustrated
in
figure
(6.22)
and as
already introduced
in
section
(5.2),
the
global
parameterization
of a
surface
S
embedded
in the
JR
space consists
of a
one-to-one mapping between
S and a
domain
D of
JR
2
called
the
"parametric"
domain:
• To any
point
u
=
(it
1
,
u
2
)
belonging
to
D,
direct
mapping
x(u)
associates
one
single
point
x(u)
=
x(ii
1
,'U
2
)
belonging
to S.
• To any
point
x =
(x
1
,
x
2
, x
3
)
belonging
to S,
inverse
mapping
u(x)
associates
one
single
point
u(x)
=
u(x
1
,x
2
,x
3
)
belonging
to D.
In
this
section,
it is
assumed
that
the
geometry
of S is
given
and the
goal
is
to
build
the
functions
u(x)
and
x(u).
By
opposition
to the
local
parametric
representations introduced
in
section (6.1.3),
the
function
x(u)
so
defined
is
called
a
global
parametric representation
of S
while
the
function
u(x)
is
called
a
global
parameterization
of
S.
6.5.1
Introduction
Linear
model
For
simplicity's sake,
it is
assumed
that
S is
modeled
as a
triangulated surface
T(S}
where
any
triangular
facet
T €
T(S]
is a
(flat)
linear
patch
(see
definition
(6.10)).
The set
Q
of
vertices
of
T(S]
defines
a
sampling
of
both
S and D, and the
same notations (see page 247)
are
used
for
designing
the
287
