Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.


328
CHAPTER
7.
CURVILINEAR
TRIANGULATED SURFACES
Nature
of the
edge
E(p
0
,p
l
)
The
edge
E(p
0
,
p
1
)
corresponding
to the
boundary
of the
patch between
the
points
PO
and
p
l
is
generated
by the
points
x(u,
v)
for
which
the
parameter
v
is
equal
to
zero:
Thus,
the
edge
£'(p
0
,p
1
)
has an
equation
x(w)
such
that
Moreover,
the
derivatives
on
this
edge
are
such
that
Prom
these expressions,
it can be
deduced
that
the
edge
J
E(p
0
,p
1
)
has the
following
properties:
• The
equation
x(u)
=
x(u,
0)
depends
solely
on
p
0
,
p
1?
N
0
,
and
Nj.
• The
tangent
x
u
('U,0)
to the
patch
T(p
0
,p
1
,p
2
)
is
identical
to the
tangent
x
w
(it)
to the
curve
E(p
0
,p
l
)
and
depends
solely
on
p
0
,Pi,
N
0
,
and
N!.
• The
tangent
x«(u,
0) to the
patch
T(p
0
,p
1
,p
2
)
depends
not
only
on
p
0
,
p
x
,
NO,
and
N
l5
but
also
on the
central
point
q.
The two
last properties imply
that
the
normal vector
N(w,
0) on the
boundary
JE?(p
0
,Pi)
of the
patch
T(p
0
,p
1
,p
2
)
depends
not
only
on
p
0
,
p
1;
N
0
,
and
N
1;
but
also
on the
central point
q.
Shape
of the
patch
T(p
0
,p
1
,p
2
)
Verifying
that
equation
x(w,
v}
honors
the
convex hull property relative
to
B
3
is
possible.
Due to the
fact
that
r(p
0
,p
1
,p
2
)
interpolates
the
three vertices
p
0
,
p
l5
and
p
2
and is
tangent
to the
unit vectors
Tij
=
(3
•
(PJ
—
p
f
),
how
83
"controls"
the
shape
of the
patch
T(p
0
,
p
1?
p
2
)
can be
envisaged,
as
shown
in
figure
(7.7).
As
a
consequence
of
these properties
of the
Control-Net
83,
it is
concluded
that
this Control-Net should
be
chosen
in
such
a way
that
it
looks like
a
polyhedral approximation
of the
patch
T(p
0
,p
1
,p
2
).
This
suggests
how to
choose
the
parameter
(3 and the
function
0(-)
used
to
define
the
points
p^
•
and q of the
Control-Net;
for
example,
the
following choices yield generally
good
results
in
practical applications:
and

7.2.
BUILDING
A
SMOOTH CURVILINEAR TRIANGLE
Symmetry
of
equation
x(w,
v)
As can be
seen, equation
x(w,
v)
remains
formally
unchanged
if the
following
circular permutations
of the
indices
(0,1,2)
and the
parameters
(w,u,v)
are
performed
simultaneously:
Consequently,
all
that
has
been said
about
the
edge
E(p
0
,
p
x
)
is
also valid
for
the two
other edges
of the
patch.
7.2.4
Degenerated
quartic
Bezier
patch
Degree
elevation
Let
x.s(u,v)
be the
cubic Bezier patch introduced
in the
previous section:
To
increase
the
"flexibility"
of
x
3
(<u,i>),
it is
necessary
to add
Control-Nodes,
which
can be
done
by
considering
q as a
linear function
of
three
new
Control-
Points
q
0
,
qj,
and
q
2
:
Assuming,
provisionally,
that
these three additional Control-Nodes
are
defined
by
the
three
following
equation
it
is
deduced
that
which
implies
that
It can be
concluded
that
the
degree
of
X3(w,
v}
can be
increased without chang-
ing
the
geometry
of the
patch
as
long
as the
conditions (7.5)
are
respected:
329
and

330
CHAPTER
7.
CURVILINEAR TRIANGULATED SURFACES
Figure
7.8 An
example
of
a
curvilinear
triangular
patch
T(p
0
,p
1
,p
2
)
and its
associated
degenerated
quartic
Bezier
Control-Net.
If
the
conditions (7.5) above
are not
respected, this equation
is
still valid,
but
can no
longer
be
considered
as a
cubic
patch.
In
this
case,
no
more simplifi-
cation occurs
and
^(u,v)
becomes
an
actual fourth-degree polynomial. This
forms
the
basis
of the
notion
of
degenerated quartic Bezier patch presented
in
this section.
Bezier
Control-Net
B\
The
degenerated quartic
Bezier
Control-Net
B^
corresponds
to the
points
shown
in
figure
(7.8)
and is
deduced
from
the
cubic Control-Net
3%
by
replac-
ing
the
node
q by the
three nodes
q
0
,
^,
and
q
2
introduced above:
Definition
of
x(u,
v)
Let us
consider
the
following
equation
x(w,
v)
where
w = (1
—
u
—
v):
As
can be
seen,
the
polynomials used
as
weighting
in
this equation
are of
degree
4, but
there
are no
terms
w
4
,
u
4
,
and
w
4
,
and
x(w,
v) can be
considered

7.2.
BUILDING
A
SMOOTH CURVILINEAR TRIANGLE
as a
"degenerated" polynomial
of
degree
4.
Therefore,
the
piece
of
surface
^(PO'
Pi?
P2)
whose
points
x(u,v)
are
denned
by the
above equation
is
called
"degenerated quartic Bezier patch" based
on
B\.
It is
easy
to
verify
that
Comment
The
degenerated quartic Bezier patch
has
been
presented
briefly
to
introduce
the
notion
of
Gregory patch, which
will
be
developed
in the
next section.
In
practice,
the
degenerated quartic Bezier patch
has the
same behavior
as the
cubic
one
relative
to its
Control-Net:
• For the
authorized
values
(it,
v)
6
DT,
the
polynomial
weighting
coefficients
of
the
points
belonging
to the
Control-Net
B\
are
positive
and
have
a sum
equal
to 1 so
that
the
"convex
hull"
property
is
still
honored.
• The
equation
x(it)
of the
edge
E(p
0
,p
1
)
is
strictly
identical
to the one ob-
tained
in the
case
of the
cubic
Bezier
patch
and
depends
only
on the
Control-
Nodes
p
0
,
p
01
,
p
10
,
and
P!.
• The
normal
vector
N(ii,
v) on the
edge
E(p
0
,
Pi)
depends
not
only
on
(p
0
,
N
0
)
and
(pijNi),
but
also
on the
central
points
q
0
and
q
x
.
• The
equation
x(w,
v)
remains
formally
unchanged
when
a
circular
permuta-
tion
is
performed
simultaneously
on the
indices
(0,1,2)
and the
parameters
(w,u,v).
7.2.5 Gregory
patch
As
shown
in
figure
(7.11),
the
ultimate goal with triangular patches
is to
assemble them into
a
patchwork
to
achieve
a
piecewise parametric represen-
tation
of a
triangulated surface such
as the one
shown
in
figure
(7.1).
This
raises
two
problems:
1.
how to
ensure
that
there
is no gap
between
two
adjacent
triangular
patches,
and
2.
how to
ensure
that
the
normal
vector
N(M,
v)
will
be
continuous
across
the
common
edge
of any
pair
of
adjacent
triangles.
Problem
(1) is
relatively simple
to
solve,
but
problem
(2) is
quite complex
and is
still
an
active
field of
research (see [47,
57, 75,
140, 167, 173,
225],...).
Among
the
many possible solutions,
we
will
present
one
initially proposed
by
Du
and
Schmitt [64, 65], based
on an
earlier technique developed
by
Gregory
[96,
97] and
extended
to
Bezier patches
by
Chiyokura
and
Kimura
[47].
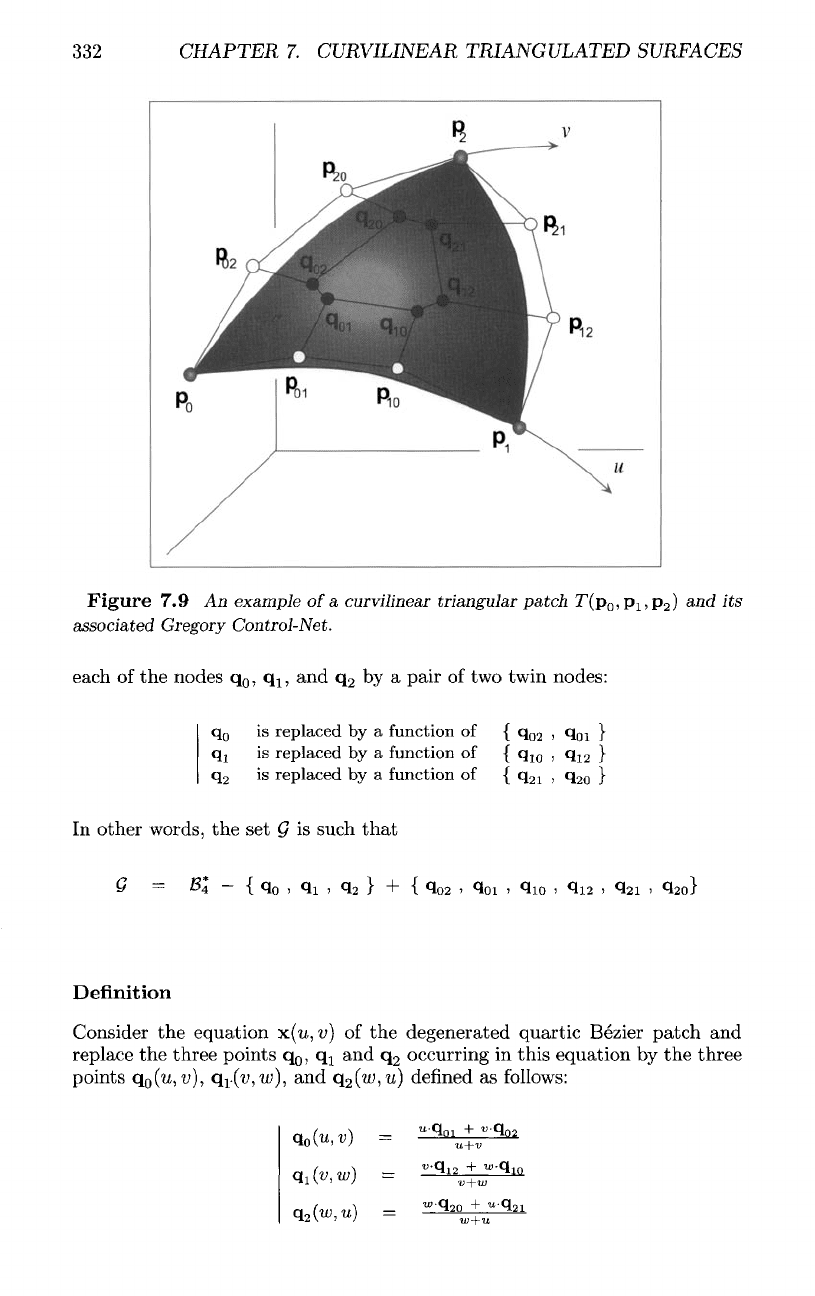
The
Gregory
Control-Net
Q
The
Gregory Control-Net
Q
corresponds
to the
points represented
in figure
(7.9)
and
deduced
from
the
degenerated quartic Control-Net
B%
by
replacing
331
332
CHAPTER
7.
CURVILINEAR TRIANGULATED SURFACES
Figure
7.9 An
example
of
a
curvilinear
triangular
patch
T(p
0
,p
1
,p
2
)
and its
associated
Gregory
Control-Net.
each
of the
nodes
q
0
,
q
l5
and
q
2
by a
pair
of two
twin nodes:
In
other words,
the set
Q
is
such
that
Definition
Consider
the
equation
x(u,
v)
of the
degenerated quartic
Bezier
patch
and
replace
the
three points
q
0
,
qj
and
q
2
occurring
in
this equation
by the
three
points
q
0
(w,
i>),
<i
v
(v,w),
and
q
2
(w;,w)
defined
as follows:

7.2.
BUILDING
A
SMOOTH CURVILINEAR TRIANGLE
These modifications induce
a new
equation
for
x(w,i>),
and the new
patch
so
obtained
is
called
the
"Gregory
patch:"
For the
authorized values
(w,
v) 6
DT,
the
(polynomial
and
fractional) weight-
ing
coefficients
of the
points belonging
to the
Control-Net
Q
are
positive
and
have
a sum
equal
to 1, so
that
the
"convex hull" property
is
still honored.
Tangents
x
u
(w,v)
and
x
v
(u,v]
The
tangents
in the u and v
directions
can be
obtained
by
deriving
the
equa-
tion
x(w,
v) of the
cubic Gregory
patch:
333

334
CHAPTER
7.
CURVILINEAR
TRIANGULATED
SURFACES
Figure
7.10
Radial
direction
{(M
O
,
0),
(0,1)}.
Taking into account
the
fact
that
w =
I
—
u
—
v,
we can
easily compute
the
derivatives
of
q
0
(w,-u),
q
1
(v,
w;),
and
q
2
(w,
u}
in the
above
formula:
Radial
tangent
x
r
(w,
0)
As
shown
in
figure
(7.10),
let us
consider
the
"radial" segment joining
the
point
of
coordinate
(uo,0)
on the u
axis
of the
triangle's
DT
to its
opposite
vertex
(0,1).
The
parametric equation
of
this
radial
segment
is
We
will
call "radial tangent"
of
x(u,
v) at
(wo,0)
the
vector
x
r
(wo,0),
as
denned
by
Let
g(w,
v,
w) be the
equation
x(w,
v)
considered
as a
function
of
three vari-
ables
(u,v,w}.
It can
always
be
written
as
follows:

7.2.
BUILDING
A
SMOOTH
CURVILINEAR
TRIANGLE
Note
that
the
partial derivatives
in the
above expression
are
such
that
From these expressions
and for any u =
UQ,
it can be
deduced
that
Nature
of the
edge
£'(p
0
,p
1
)
The
edge
E(p
0
,p
l
)
corresponding
to the
boundary
of the
patch between
the
points
PO
and
p
l
is
generated
by the
points
x(w,
v)
for
which
the
parameter
v is
equal
to
zero:
The
edge
E(p
0
,p
l
)
has
thus
an
equation
x(w)
such
that
Moreover,
the
axial
tangent
x
u
(w,
0) and the
radial
tangent
x
r
(w,0)
on
this
edge
are
such
that
From these axial
and
radial tangents,
the
normal vector
N(u,
0)
along
the
edge
E^PO^)
can be
computed
as
follows:
From
these
expressions,
it can be
deduced
that
the
edge
£'(p
0
,p
1
)
has the
following
interesting properties:
335

336
CHAPTER
7.
CURVILINEAR
TRIANGULATED
SURFACES
Figure
7.11
A
patchwork composed
of
Gregory
triangular patches
and
associated
network
of
Gregory
Control-Points.
• The
equation
x(«)
of the
edge
E(p
0
^p
l
)
is
strictly identical
to the one ob-
tained
in the
case
of the
cubic Bezier patch
and the
degenerated quartic Bezier
patch.
In
particular, this edge depends only
on the
Control-Points
p
0
,
p
01
,
Pio>
and
Po-
• The
normal vector
N(w,i>)
on the
edge
E(p
0
,p
l
)
depends only
on the
nodes
directly
linked
to
this edge
by the
links represented
in figure
(7.9).
In
par-
ticular,
it can be
noted
that
N(ti,
v)
does
not
depend
on
inner Control-Points
other
than
q
01
and
q
10
.
As
a
consequence,
when
considering
the two
adjacent
patches
T(p
0
,p
1
,p
2
)
and
T(p
0
,p
1
,p
2
),
which
share
the
common
edge
E(p
Q
,p
l
),
figure
(7.12)
shows
that
it
should
be
possible
(see
[65])
to
adjust
the
locations
of the
points
(q
01
,q
10
)
and
(qoi>qio)
as
functions
of
(p
2
,N
2
)
and
(p
2
,N
2
)
to
ensure
the
continuity
of the
normal
vector
through
the
common
edge
-E^Po,
P]_):
This
is the
origin
of the
method
presented
in the
next
section.
7.3
Gregory
G
l
patchwork
7.3.1
Introduction
Geometric continuity
As
suggested
in figure
(7.11),
let us
consider
a
patchwork
consisting
of a set of
adjacent
(triangular)
patches.
According
to
section
(5.4.4),
such
a
patchwork
is
said
to be
"geometrically
continuous"
or,
more
simply,
G°
continuous
if the
following
condition
is
respected:
• For any
pair
of
adjacent patches (triangles)
T(p
0
,p
l5
p
2
)
and
T(p
0
,p
1
,p
2
),
there
is no gap
along their common edge
E(p
0
,p
1
);
in
other words,
and as
7.3.
GREGORY
Gl
PATCHWORK
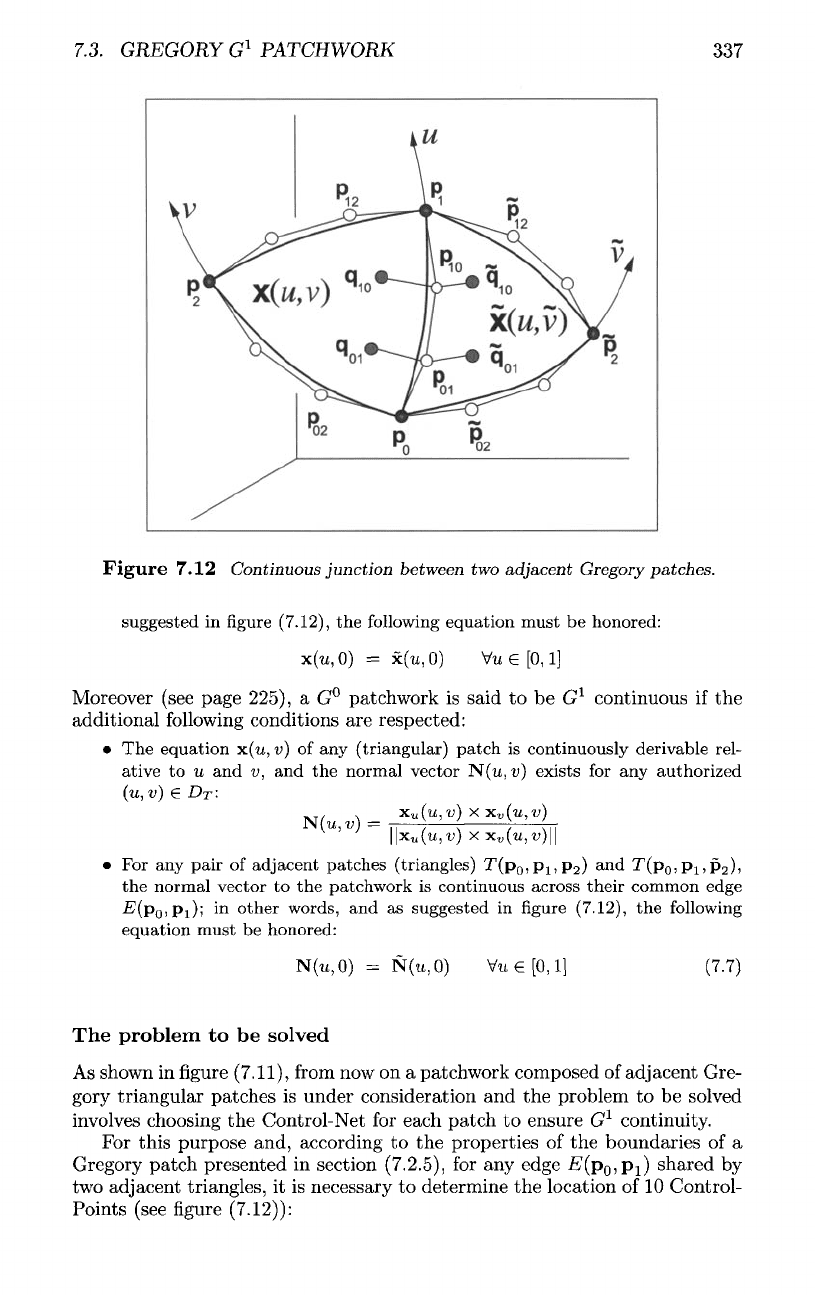
Figure
7.12
Continuous
junction
between
two
adjacent
Gregory
patches.
suggested
in figure
(7.12),
the
following
equation must
be
honored:
Moreover
(see page 225),
a
G°
patchwork
is
said
to be
G
l
continuous
if the
additional
following
conditions
are
respected:
• The
equation
x(it,
v)
of any
(triangular)
patch
is
continuously derivable
rel-
ative
to u and v, and the
normal vector
~N(u,v)
exists
for any
authorized
(u,v)
G
D
T
:
• For any
pair
of
adjacent patches (triangles)
T(p
0
,p
1
,p
2
)
and
T(p
0
,p
1
,p
2
),
the
normal vector
to the
patchwork
is
continuous across their common edge
•^(Po'Pi);
m
other
words,
and as
suggested
in figure
(7.12),
the
following
equation must
be
honored:
The
problem
to be
solved
As
shown
in
figure
(7.11),
from
now on a
patchwork composed
of
adjacent Gre-
gory
triangular patches
is
under consideration
and the
problem
to be
solved
involves
choosing
the
Control-Net
for
each
patch
to
ensure
G
l
continuity.
For
this purpose and, according
to the
properties
of the
boundaries
of a
Gregory
patch presented
in
section
(7.2.5),
for any
edge
E(p
0
,p
l
)
shared
by
two
adjacent triangles,
it is
necessary
to
determine
the
location
of 10
Control-
Points
(see
figure
(7.12)):
337
