Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.

478
CHAPTER
9.
STOCHASTIC MODELING
9.4.2 Building
a
stationary
p-dimensional
RFS
Let
u and
{/i,...,
f
p
}
be a
p-dimensional
vector
and a
series
of p
letters
"c"
or
"s,"
respectively such
that
and let
Z^
1
'"^(u,
u;)
be an
associated
family
of
random
functions,
as
denned
by
Using
these notations,
it is
easy
to
extend
the
one-dimensional random
func-
tion
generator presented
in the
above section
to
obtain
a
p-dimensional
ran-
dom
function
generator.
For
this purpose,
the
random
function
Z(u,u))
is
denned
by
where
the
random
functions
Z%
(u,
u;)
and
Z|
(u,
LJ)
are
themselves
defined
recursively
as
follows:
If
the
Random Variables
{Z^"
^{uj}}
are
assumed
to be
independent
26
such
that
26
See the
definition
on
page
453.

9.4.
RANDOM FOURIER SERIES
then,
for all u £ [0,
27r]
p
,
it is
verifiable
that
the
mean value
and the
covariance
function
of
Z(u,u))
are
such
that
where
{/i
1
,...,
h
p
}
are the
components
of h in the
parametric space:
In
other words,
Z(u,
a;)
is a
centered second-order stationary random
function
whose
stationary covariance
function
C^(h)
is
defined
by
where
h
represents
a lag in the
[—2yr,
+2yr]
p
domain.
Once
again,
the
parameters
defining
Z(u,
u]
are the
coefficients
{cr
2
^
k
}
and the
degrees
{Ki,..
.,K
P
}
of the
polynomials used
in
equations
(9.65),
(9.66)
and
(9.67).
In
practice, just
as in the
one-dimensional case,
the
coeffi-
cients
{crjk
k
} are
determined
in
such
a way
that
where
cov(h)
is a
given
"target"
p-dimensional
stationary covariance function
assumed
to
capture
the
"style"
27
of the
random function
Z^u,a>)
to be
built.
Comparing equations
(9.67)
and
(9.68),
we can
write
This
suggests interpolating
the
target function
cov(h)
by a
trigonometric poly-
nomial
with
the
following
form
where
the
coefficients
{cr
ki
k
} are
determined
to
honor
the
equation
(9.69)
as
well
as
possible.
For
example,
if we
choose
to
interpolate
the
series
of
points
{hji-.-jp}
belonging
to ]0,
TT]
P
and
defined
by
27
See
section
(9.4.6)
479

480
CHAPTER
9.
STOCHASTIC
MODELING
then,
using
the
functions
^(fc,
h)
as
defined
by
equation
(9.63),
we
obtain
As
in the
one-dimensional
case,
it can be
checked
that
these
values
{a
2
k
}
are
always
positive
provided
that
the
given
covariance
function
cov(h)
honors
the two
following
conditions:
28
The
only
parameters
of the
p-dimensional
random
function
Z(u,
u;)
presented
above
are the
degrees
{Ki,...,
K
p
}
and the
covariance
function
cov(h)
of
the
trigonometric
polynomial
Z(u,
w).
In
practice,
these
parameters
can be
chosen
as
follows:
• The
covariance
function
ccw(h)
is
assumed
to
have
the
form
where
covi(h)
is a
one-dimensional covariance
function
(see page 464)
and
[R
2
]
is a
symmetrical positive
definite
range matrix (see page 464):
As
in the
one-dimensional case,
the
range matrix
is
chosen
to fit the
"prior"
knowledge
of the
"style"
29
of the
random
function
Z(u,a>).
•
Degrees
(Ki,...,K
p
)
of the
polynomial must
be
large enough
to
achieve
a
good approximation
of
equation
(9.69).
To
this purpose,
a
strategy similar
to the one
used
for the
one-dimensional case (see page 477)
can be
used.
Moreover,
to
minimize
the
number
of
terms
in the set
/C,
a
rule
of
thumb
is
to
perform
a
rotation
of the
coordinate system
for the
components
u
l
of u to
become parallel
to the
iih
eigen vector
of the
range matrix
[R
2
].
9.4.3
Ergodicity
Let
us
consider
the
one-dimensional
RFS
Z(w,u;),
as
denned
by
equation
(9.57),
and let ra|(u;) and
C^(h,
u]
be the
associated spatial mean
and
spatial
covariance
functions:
28
This
is a
sufficient,
not a
necessary,
condition.
29
See
section
(9.4.6)

9.4.
RANDOM FOURIER SERIES
481
Using
the
notations
(9.55)
and the
orthogonality
of the
sin(-)
and
cos(-)
func-
tions
on [0,
2-Tr],
it can be
shown
that
According
to
equations
(9.56),
where
m^
and
C^(h)
are the
(statistical) mean
and
covariance
functions
of
Z(u,(jj\
respectively. From equation (9.33),
it can
also
be
deduced
that
where
7|(fo)
and
7^(/0
are the
spatial
and
statistical
variograms
of
Z(u,u),
respectively.
This shows
that
•
Z(u,uj)
is
order
1
weakly
ergodic,
and
•
Z(u,u))
is
order
2
weakly
ergodic.
In
fact,
as
soon
as the
range
of
C^(h]
is
less
than
3?r/2,
it can be
observed
experimentally
that
Similar
results
can be
obtained
for the
p-dimensional
random
function
Z(u,
w),
as
denned
by
equation
(9.65).
9.4.4
Gaussian
behavior:
Notion
of
GRFS
~"
f f
The
fact
that
the
Random Variables
Z
k
l
"
k
p
used
in
equations
(9.65)
and
(9.66)
to
build
a RFS
Z(u,
LJ]
are
centered implies
that
Z(u,
cu]
is a
centered
random
function:
~
f f
Let
us
assume
that,
in
addition,
all the
Random Variables
Z^"
k
p
have
the
same
type
of
cdf's.
In
such
a
case,
for any fixed
value
of
u,
it can be
observed
from
equations
(9.65)
and
(9.66)
that
2T(u,o;)
is the sum of K =
(Ki-K
2
..
.K
p
]
independent Random Variables having
the
same type
of
cdf.
As
soon
as K is
large
enough, according
to the
"central limit" theorem (see page 454),
it can
be
deduced
that
2/(u,
u;)
is a
centered
Gaussian
Random
Variable
In the
rest
of
this book,
any
random Fourier series honoring both conditions
(9.72)
and
(9.73)
will
be
called
a
(centered) Gaussian Random Fourier Series
or,
more simply,
a
GRFS.
482
CHAPTER
9.
STOCHASTIC MODELING
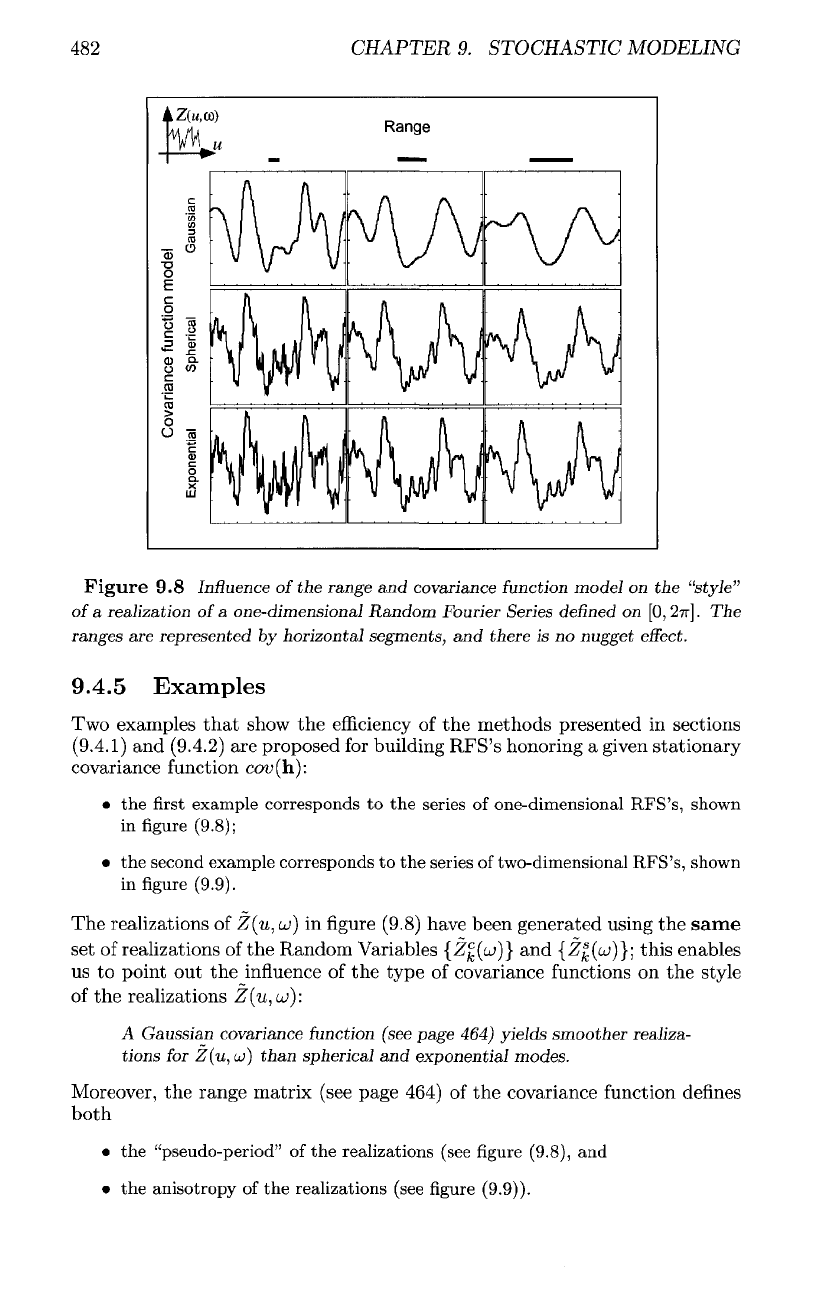
Figure
9.8
Influence
of
the
range
and
covariance function model
on the
"style"
of
a
realization
of a
one-dimensional
Random
Fourier Series
defined
on [0,
2?r].
The
ranges
are
represented
by
horizontal segments,
and
there
is no
nugget
effect.
9.4.5
Examples
Two
examples that show
the
efficiency
of the
methods presented
in
sections
(9.4.1)
and
(9.4.2)
are
proposed
for
building RFS's honoring
a
given stationary
covariance
function
cov(h):
• the first
example corresponds
to the
series
of
one-dimensional RFS's, shown
in figure
(9.8);
• the
second example corresponds
to the
series
of
two-dimensional
RFS's,
shown
in figure
(9.9).
The
realizations
of
Z(n,
u)
in
figure
(9.8) have been generated using
the
same
set of
realizations
of the
Random Variables
{Z%(u})}
and
(Z|(a;)};
this enables
us to
point
out the
influence
of the
type
of
covariance
functions
on the
style
of
the
realizations
Z(u,u)}:
A
Gaussian covariance function (see page 464) yields
smoother
realiza-
tions
for
Z(u,u))
than
spherical
and
exponential modes.
Moreover,
the
range matrix
(see
page 464)
of the
covariance
function
defines
both
• the
"pseudo-period"
of the
realizations
(see
figure
(9.8),
and
• the
anisotropy
of the
realizations
(see
figure
(9.9)).

9.4.
RANDOM FOURIER SERIES
Figur e
9.9 An
example
of
multiple equiprobable realizations
of
a
two-dimensional
P-field
on [0,
TT]
in
the
case
of an
anisotropic range
ellipsoid
(drawn
in
white)
and a
Gaussian
covariance function. Values close
to 0 are
coded
in
light grey while values
close
to 1 are
coded
in
dark grey.
9.4.6
About
the
"style"
of a
Random Function
All
through
the
previous sections
of
this chapter
the
term "style"
of a
random
function
has
been used without
giving
an
exact
definition:
it was
simply
stated
that
this style
is
controlled
by the
covariance
function.
The
examples
presented
in figures
(9.8)
and
(9.9) suggest
that
the
notion
of
style
is
composed
of
three parts:
• the
behavior
of a
random
function
is
controlled
by the
type
of its
covariance
function:
a
Gaussian covariance
function
yields smoother realizations
than
spherical
and
exponential models;
• the
pseudo-period
of a
random
function
is
controlled
by the
magnitude
of
the
range
of the
covariance
function:
two
main
extrema
of a
realization
are
approximately distant
of
half
of the
range;
• the
amplitude
of
local variations
of a
random
function
are
approximately
equal
to the
square root
yC(0)
of the
covariance
function
at the
origin.
483

484
CHAPTER
9.
STOCHASTIC MODELING
9.4.7
Random Function defined
on a
bounded support
Let
D be a
bounded domain
in the
parametric space
M
p
,
and let
D
n
be the
smallest parallelepipedic region containing
D and
denned
as
follows:
Assuming
that
h
l
min
<
h
l
max
for
each
i,
u can
always
be
denned
as a
vectorial
function
of u
such
that
The
reparameterization
u(u)
so
denned
is
obviously invertible:
Prom
a
theoretical point
of
view,
this
shows
that
any
random
function
Z(u,
a;)
whose
realizations
are
denned
and
integrable
on the
bounded domain
D
con-
tained
in
D
D
can be
approximated
by a
Random Fourier Series
Z(u,
uo]
defined
on
[0,
27r]
p
with
a
period equal
to
2?r
in
each direction
of the
parametric space:
As
a
consequence,
all the
properties presented
in
section (9.4)
for
Random
Fourier Series
are
also valid
for
random
functions
whose realizations
are de-
nned
and
integrable
on a
bounded support
D.
9.4.8
Sampling
a
GRFS
on a
regular
p-grid
In
many applications, realizations
of a
GRFS
Z(u,u})
must
be
generated
at
each node
of a
regular
p-grid.
In
such
a
case
and as
shown
in
this
section,
the
formalism
of the
Discrete Fourier
transform
(e.g.,
see
[238,
45])
can be
applied
to the
representation
of
Z(u,
LJ)
. The
greatest
benefit
of
such
a
discrete
representation
is to
allow
a
very
fast
computation
of
Z(u,u;)
at the
nodes
of
the
grid
thanks
to the
Fast
Fourier Transform (FFT) algorithm.
Discrete
representation
of a
GRFS
on a
1-grid
Let
us first
examine
the
case where
Z(u,w)
defined
by
equation
(9.57)
has to
be
computed
on [0,
2?r[
at
equally spaced nodes
{u
n
:
n =
0,...,
K — 1} of a
regular 1-grid
defined
by
In
such
a
case,
the
sampling
of
Z(u,
u) at the K
nodes
of the
grid generates
a
periodic series
of K
Random Variables:

9.4.
RANDOM FOURIER SERIES
Using
the
well-known complex trigonometric
formulae
30
allows
the
discrete version
of
equation
(9.57)
to be
written
as
with
According
to
equations
(9.56),
these Random Variables
are
such
that
31
Referring
to
equations
(9.55),
Zk(w}
can be
turned into
the
following
integral:
Replacing
du by the
increment
Aw
=
27T/K
and
using
the
sampling
denned
by
the
equations
(9.74)
allows this integral
to be
approximated
as
follows:
At
this point,
let us
recall
the
definition
of the
notions
of
(direct) Discrete
Fourier Transform (DFT)
and
inverse Discrete Fourier Transform
(e.g.,
see
[93,
45]):
• the
direct
Discrete
Fourier
Transform
of a
series
{X*}
=
{Xo,..
.,XK-I}
is a
series
{^0}
=
{Xo,...,
XK-I}
as
defined
by
• the
inverse
Discrete
Fourier
Transform
of a
series
{^o}
=
{Xo,
• •
-,XK-I}
is
a
series
{X*}
=
{Xo,...,
XK-I}
as
defined
by
30
In
these
formulae,
i is the
pure
imaginary
number
i =
•\/—'i.
31
Here,
\z =
\/a
2
+ b
2
represents
the
modulus
of z = a + ib.
485

486
CHAPTER
9.
STOCHASTIC MODELING
• the
following
relationships always hold
true:
For
each
fixed
elementary event
uj
G 0, the
complex value
Zk(u)
defined
by
equation
(9.79)
is no
more than
the
Discrete Fourier Transform
of the
function
Z(u,
ui)
sampled
on the
regular
1-grid
at
nodes
u
n
defined
by
equations
(9.74).
Consequently,
the
inverse Discrete Fourier Transform
defined
by
can
generate
the
associated sampled values
Z(itfc,u;)
for any
given integer
k
=
Q,...,K-l.
Taking into account
the
independence
of the
RV's
{Zk},
it can be
derived
from
equations (9.78)
and
(9.79)
that
32
This clearly shows
that
the
series
{a\
:
k = 0,
...,K
—
1}
is the
inverse
Discrete Fourier Transform
of the
series
{C
m
: ra
=
0,..
.,K
—
1}
defined
by
C
m
~
Cz(mAu).
As a
consequence,
the
direct Fourier Transform allows
the
coefficients
a\
to be
computed
at the
nodes
of a
regular 1-grid
as
follows:
Fast
generation
of a
GRFS
on a
regular
1-grid
The
twin equations
(9.79)
and
(9.80)
with equation
(9.82)
form
the
basis
of
a
very fast algorithm
for
generating realizations
of a
GRFS
at the
nodes
of a
1-grid;
to
this end, proceed
as
follows:
1.
use the
direct
Fast
Fourier Transform algorithm (e.g.,
see
[93])
to
compute
the
series
of
coefficients
{cr
0
,...,
&K-I}
from the
following sampling
of a
given
(periodic) covariance function
C^(K):
2.
draw,
at
random,
a
series
uj
=
{Oo,
• •
-,
OK-I}
of K
angles uniformly dis-
tributed
on [0,
2?r[;
32
Here
~z
= a
—
ib
represents
the
conjugate
of z
=
a + ib.

9.4.
RANDOM FOURIER SERIES
487
3.
build
a
series
of K
numbers
{Zo(u),...,
ZK-\(U}}
defined
33
by
4.
use the
inverse
Fast
Fourier
Transform
algorithm
to
compute
the
values
Z(u
n
,u]
defined
by
equation
(9.80)
at the
nodes
of the
regular
1-grid.
There
is a
pitfall
to be
avoided
at
step
1 of
this process: generally,
one
chooses
a
given covariance function
cov(h)
similar
to one of
those
presented
on
page
464,
and it is
tempting
to
interpret equation (9.83)
as
follows:
However,
according
to
equation
(9.59),
it is
clear
that
C^(h]
must
be a
peri-
odic
function
with
a
period equal
to
2yr
and
this
is
generally
not the
case
for
cov(h}:
consequently,
the
above
definition
of the
coefficients
C
m
cannot
be
used.
Due to
this
periodicity
of
C^(h\
it can be
observed
that
As
a
consequence,
in the
case where
the
range
of
cov(h)
is
lower
than
TT,
the
above
difficulty
can be
avoided
if
step
1 of the
fast algorithm
is
itself broken
down
into
the
three
following
substeps:
•
determine
the
greater
integer
M
such
that
MAu
is
lower
than
TT
and
compute
the
sequence
{Co,...,
CM}
as
follows:
• use
equation
(9.83)
to
complete
the
sequence
{Co,...,
CK-I}'
• use the
direct
Fast
Fourier
Transform
algorithm
to
compute
the
series
of
co-
efficients
{<TO,
...,
cr|
r
_
1
}
from
the
above
series
of
coefficients
{Co,...,
CK-I}-
Generalization
to
regular
p-grids
The
notions
of
Discrete Fourier Transform
and
Fast
Fourier Transform
can
easily
be
generalized (e.g.,
see
[93])
to the
case
of
functions sampled
at the
nodes
{u
ni
...
np
}
of a
regular
p-grid
covering
the
domain
[0,2?r[
p
and
defined
by
33
Note
that
the
RV's
Z^
so
denned
are
independent,
have
the
same cdf,
and
honor
the
conditions
(9.78).
