Jacques I. Mathematics for Economics and Business

Подождите немного. Документ загружается.

Dynamics

580

Example

Consider the market model

= 3P − 4

=−5P + 20

= 0.2(Q

− Q

)

Find expressions for P(t), Q

(t) and Q

(t) when P(0) = 2. Is this system stable or unstable?

Solution

Substituting the expressions for Q

and Q

into

= 0.2(Q

− Q

)

gives

= 0.2[(−5P + 20) − (3P − 4)] =−1.6P + 4.8

The complementary function is given by

CF = Ae

−1.6t

and for a particular solution we try

P(t) = D

for some constant D. Substituting this into the differential equation gives

0 =−1.6D + 4.8

which has solution D = 3. The general solution is therefore

P(t) = Ae

−1.6t

+ 3

The initial condition

P(0) = 2

gives

A + 3 = 2

and so A is −1. The solution is

P(t) =−e

−1.6t

+ 3

Corresponding expressions for Q

(t) and Q

(t) can be found from the supply and demand equations,

which give

(t) = 3P − 4 = 3(−e

−1.6t

+ 3) − 4 =−3e

−1.6t

+ 5

(t) =−5P + 20 =−5(−e

−1.6t

+ 3) + 20 = 5e

−1.6t

+ 5

Note that all three expressions involve a negative exponential that converges to zero as t increases, so the

system is stable. The price P(t) eventually settles down to the equilibrium price, 3, and Q

(t) and Q

(t) both

approach the equilibrium quantity, 5.

MFE_C09b.qxd 16/12/2005 10:49 Page 580

In the previous example and again in Practice Problem 5 we noted that the single-

commodity market model is stable. If we return again to the general equation

=−α(a + c)P +α(d + b)

it is easy to see that this is always the case, since the coefﬁcient of P is negative. This follows

because, as previously stated, α, a and c are all positive.

Maple offers a range of facilities for investigating the behaviour of differential equations. The

basic instruction is dsolve which can be used either with or without an initial condition. Let

us suppose that we wish to solve a differential equation involving dy/dt, that is, we want to ﬁnd

a solution in which y is expressed as a function of t. If the equation itself is typed into Maple

and named eq1, say, and the initial condition is named as init, the solution y(t) is generated

by typing

>dsolve({eq1,init},{y(t)});

We illustrate this in the following example.

9.2 • Differential equations

581

Practice Problem

5 Consider the market model

= 2P − 2

=−P + 4

= (Q

− Q

)

Find expressions for P(t), Q

(t) and Q

(t) when P(0) = 1. Is this system stable or unstable?

MFE_C09b.qxd 16/12/2005 10:49 Page 581

Dynamics

582

Example

The value of an investment portfolio, y(t), varies over an 8-year period according to

= y(1 − y) (0 ≤ t ≤ 8)

where y is measured in millions of dollars and t is measured in years. Find expressions for the solution of

this equation in the case when the initial investment is

(a) $100 000 (b) $2 million

Plot the graphs of these solutions on the same diagram and comment on the stability of the system.

Solution

Before we solve this equation using Maple, there are two special cases worthy of note. If, at some time, t, the

value of the portfolio drops to zero, so that y = 0, then the right-hand side of the differential equation will

also be zero. The differential equation then reads

= 0

It follows that y is constant for all subsequent times. In other words, once the investment falls to zero, it

remains at this level.

The other special case is when y(t) = 1. Again the right-hand side, y(1 − y), reduces to zero and again the

differential equation becomes just

= 0

We deduce that once the value of the investment reaches 1 million, it remains at this level from that moment

onwards.

(a) To obtain the general solution using Maple we need to type in, and name, both the differential equation

and the initial condition. Unfortunately you cannot just write dy/dt and hope that Maple will recognize

this as a derivative. Instead we make use of the command diff which we used in Chapters 4 and 5. The

ﬁrst-order derivative of y with respect to t is written as diff(y(t),t) and the differential equation

itself is speciﬁed by typing

>eq:=diff(y(t),t)=y(t)*(1-y(t));

Maple displays this as

eq:= y(t) = y(t)(1 − y(t))

The initial condition, y(0) = 0.1, is entered, and named init by typing

>init:=y(0)=0.1;

We are now in a position to obtain the solution using

>dsolve({eq,init},{y(t)});

which gives

y(t) =

(b) The initial condition, y(0) = 2, is easily input by editing the line deﬁning init to give

>init:=y(0)=2;

The problem can then be re-solved by moving the cursor to the end of each line of instructions and

pressing the Enter key. The new solution is

1 + 9e

(−t)

∂

∂t

MAPLE

MFE_C09b.qxd 16/12/2005 10:49 Page 582

y(t) =

Figure 9.8 shows the graphs of both solutions, which is produced by typing

>plot({(1+9*exp(-t))^(–1),(1-0.5*exp(-t))^(–1)},t=0..8);

The graphs show that the system is stable with an equilibrium value of $1 million. The lower curve in

Figure 9.8 shows approximate exponential growth to begin with. Between years 2 and 4, the value of the

investment increases linearly before ﬁnally converging to its equilibrium value. The upper curve in

Figure 9.8 shows that if the initial value exceeds the equilibrium value, then y decays exponentially to

reach its equilibrium value.

1 −

(−t)

9.2 • Differential equations

583

Figure 9.8

Adjustment coefﬁcient The constant of proportionality in the simple macroeconomic

model, in which the rate of change of national income is assumed to be proportional to

excess expenditure.

Arbitrary constant A letter representing an unspeciﬁed constant in the general solution of

a differential equation.

Complementary function of a differential equation The solution of the differential equa-

tion, = my + c when the constant c is replaced by zero.

Differential equation An equation connecting derivatives of an unknown function.

Equilibrium value A solution of a differential equation that does not vary over time; it is

the limiting value of y(t) as t tends to inﬁnity.

General solution of a differential equation The solution of a differential equation that con-

tains an arbitary constant. It is the sum of the complementary function and particular solution.

Initial condition The value of y(0) that needs to be speciﬁed to obtain a unique solution

of a differential equation.

Particular solution of a differential equation Any one solution of a differential equation

such as = my + c.

Stable equilibrium An economic model in which the solution of the associated differential

equation converges.

Key Terms

MFE_C09b.qxd 16/12/2005 10:49 Page 583

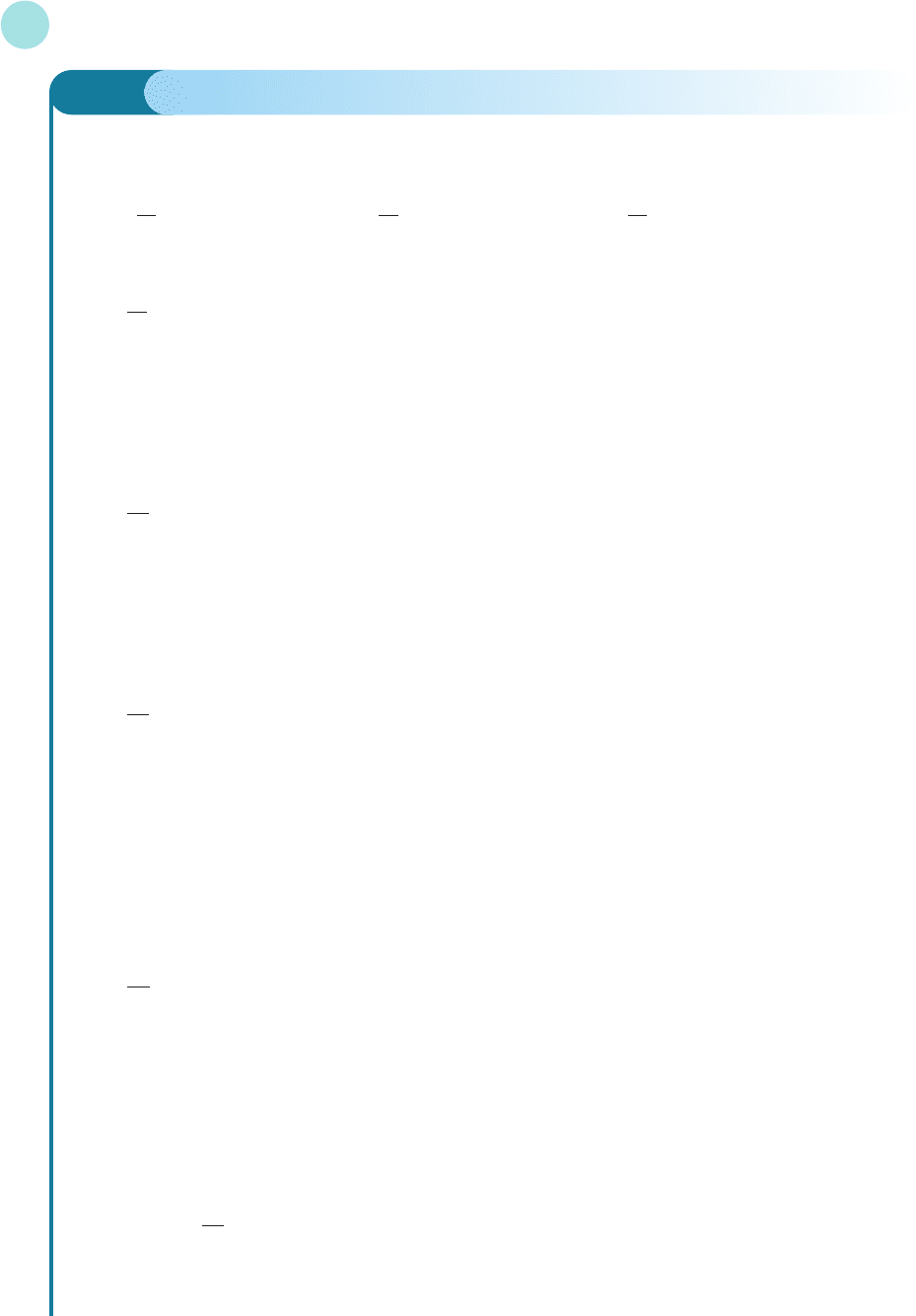
Dynamics

584

Practice Problems

6 Use integration to solve each of the following differential equations subject to the given initial

conditions.

(a)

= 2t; y(0) = 7 (b) = e

−3t

; y(0) = 0 (c) = t

+ 3t − 5; y(0) = 1

7 Solve the differential equation

=−3y + 180

in the case when the initial condition is

(a)

y(0) = 40 (b) y(0) = 80 (c) y(0) = 60

Comment on the qualitative behaviour of the solution in each case.

8 Consider the two-sector model

= 0.5(C + I − Y )

C = 0.7Y + 500

I = 0.2Y + 500

Find an expression for Y(t) when Y(0) = 15 000. Is the system stable or unstable?

9 Consider the two-sector model

= 0.3(C + I − Y )

C = 0.8Y + 300

I = 0.7Y + 600

Find an expression for Y(t) when Y(0) = 200. Is this system stable or unstable?

10 Consider the market model

= 3P − 1

=−2P + 9

= 0.5(Q

− Q

)

Find expressions for P(t), Q

(t) and Q

(t) when P(0) = 1. Is this system stable or unstable?

11 A simple model of the growth of an economy is based on three assumptions.

(1) Savings, S, are proportional to income, Y, so that

S =αY (α>0)

(2) Investment, I, is proportional to the rate of change of Y so that

I =β (β>0)

(3) Investment and savings are equal so that

I = S

MFE_C09b.qxd 16/12/2005 10:49 Page 584

Use these assumptions to show that

= Y

and hence write down a formula for Y(t) in terms of Y(0). Is this system stable or unstable?

12 Show, by substituting into the differential equation, that

y(t) = Ae

−

is a solution of

= my + c

13 Consider the differential equation

=−2y + 5e

(a) Find the complementary function.

(b) By substituting y = De

into this equation, find a particular solution.

specific solution that satisfies the initial condition, y(0) = 7.

(d) Is the solution in part (c) stable or unstable?

14 Consider the differential equation

=−y + 4t − 3

(a) Find the complementary function.

(b) By substituting y = Dt + E into this equation, find a particular solution.

specific solution that satisfies the initial condition, y(0) = 1.

(d) Is the solution in part (c) stable or unstable?

15 (Maple) Solve the differential equation

with initial condition y(0) = 1. Plot a graph of this solution on the range 0 ≤ t ≤ 5. Hence, or other-

wise, write down a simple expression for the approximate solution when t is large.

16 (Maple) In the absence of any withdrawals, the value of an investment fund, y(t), varies according to

= y(1 − y)

where y is measured in millions of dollars and t is measured in years. Money is taken out of the fund

at a constant rate of $250 000 per year so that

= y(1 − y) − 0.25

(a) Find the solution of this differential equation when the initial value of the fund is $1 million. Plot

a graph of this solution over the range 0 ≤ t ≤ 20.

+ 1

9.2 • Differential equations

585



MFE_C09b.qxd 16/12/2005 10:49 Page 585

(b) Find the solution of this differential equation when the initial value of the fund is $250 000. Plot

a graph of this solution over the range 0 ≤ t ≤ 2.

17 (Maple) The output, Q, of an Internet firm depends in the short term on capital, K, and time, t. The

production and savings functions are given by

Q = atK and S = Q − bt

respectively, where a and b are positive constants. Assuming that capital accumulation is equal to

savings, show that

= t(aK − b)

If the initial capital is c, solve this equation to obtain an expression for K in terms of t and the

constants, a, b and c. Write down the corresponding expression for Q. Comment on the qualitative

behaviour of this solution in the case when

(a)

c = b/a (b) c > b/a (c) c < b/a

Dynamics

586

MFE_C09b.qxd 16/12/2005 10:49 Page 586

Appendix 1

Differentiation

from First

Principles

We hinted in Section 4.1 that there was a formal way of actually proving the formulae for

derivatives. This is known as ‘differentiation from ﬁrst principles’ and we begin by illustrating

the basic idea using a simple example. Figure A1.1 shows the graph of the square function

f(x) = x

near x = 3.

The slope of the chord joining points A and B is

= 6 +∆x

6∆x + (∆x)

∆x

9 + 6∆x + (∆x)

− 9

∆x

(3 +∆x)

− 3

∆x

∆y

∆x

Figure A1.1

MFE_Z01.qxd 16/12/2005 10:50 Page 587

The argument given above for the particular point, x = 3, can be extended quite easily to a

general point, x. The details are are follows:

==2x +∆x

Hence

f ′(x) = lim

∆x→0

(2x +∆x) = 2x

In other words, we have proved that x

differentiates to 2x.

2x∆x + (∆x)

∆x

+ 2x∆x + (∆x)

− x

∆x

(x +∆x)

− x

∆x

∆y

∆x

Appendix 1 • Differentiation from First Principles

588

Practice Problem

1 Use differentiation from first principles to find the derivative of f(x) = x

at x = 5.

Now, as we pointed out in Section 4.1, the slope of the tangent at x = 3 is the limit of the slope

of the chords as the width, ∆x, gets smaller and smaller. In this case

slope of tangent = lim

∆x→0

(6 +∆x) = 6

In other words, the derivative of f(x) = x

at x = 3 is 6 (which agrees with f ′(x) = 2x evaluated

at x = 3). Notice that this proof is not restricted to positive values of ∆x. The chords in

Figure A1.1 could equally well have been drawn to the left of x = 3. In both cases the slope of

the chords approaches that of the tangent at x = 3 as the width of the interval shrinks.

Figure A1.2

MFE_Z01.qxd 16/12/2005 10:50 Page 588

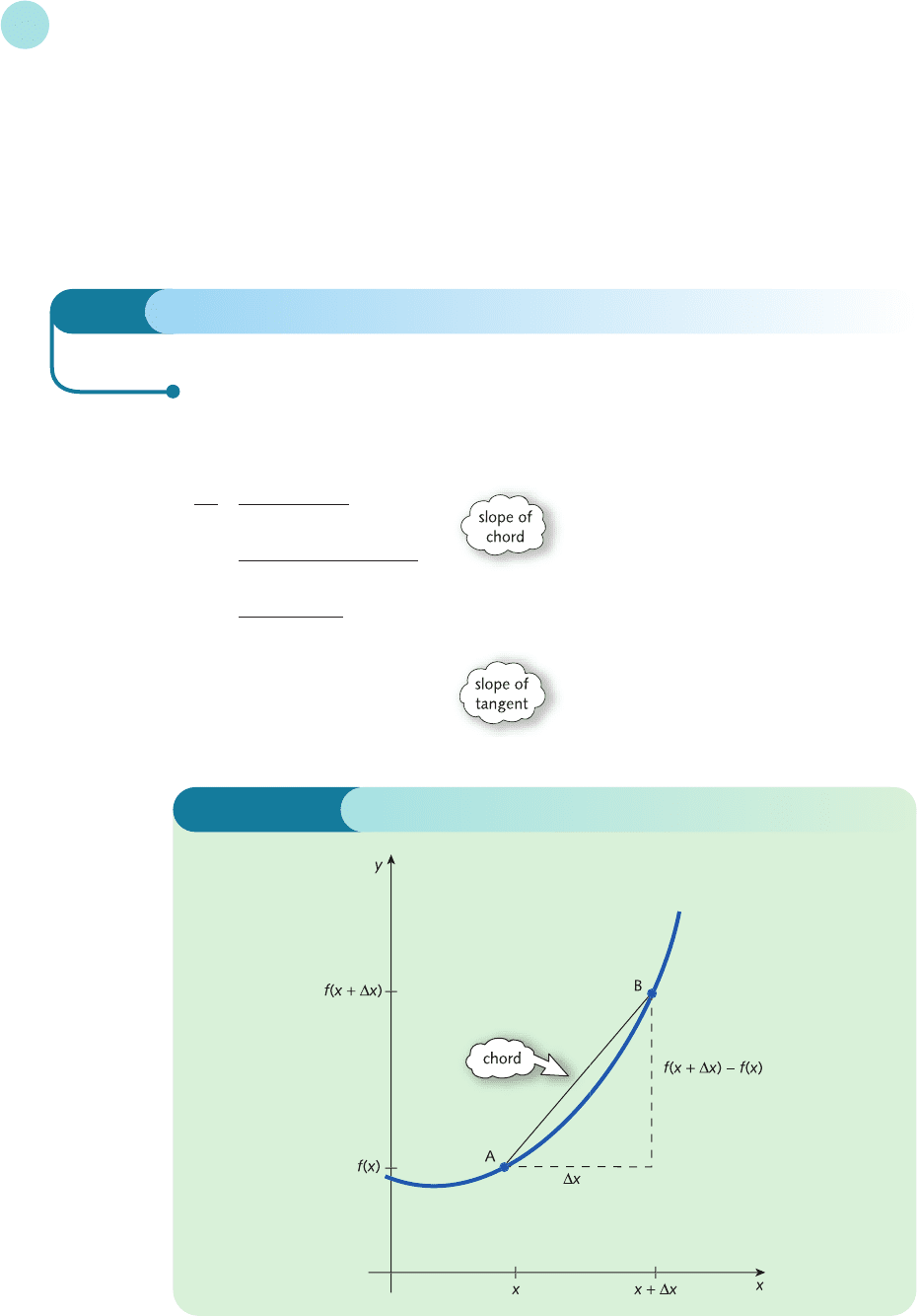
For a general function, f(x), Figure A1.2 shows that we ﬁrst ﬁnd the slope of the chord

joining A and B, i.e.

and then investigate what happens to this expression as ∆x → 0.

f(x +∆x) − f (x)

∆x

Appendix 1 • Differentiation from First Principles

589

Example

Differentiate the following functions from ﬁrst principles:

(a) f(x) = 3x

+ 5x − 6 (b) f(x) =

Solution

(a) The slope of the chord is

= 6x + 5 + 3∆x

Hence the slope of the tangent is

f ′(x) = lim

∆x→0

(6x + 5 + 3∆x) = 6x + 5

(b) The algebra is a little more complicated this time since we need to manipulate fractions. We begin by

simplifying the numerator in the fraction

Given that f(x) = , we see that

f(x +∆x) − f (x) =−

Hence

Finally, letting ∆x → 0 gives

f ′(x) ==

−1

(x + 0)x

−1

(x +∆x)x

f(x +∆x) − f (x)

∆x

−∆x

(x +∆x)x

x − (x +∆x)

(x +∆x)x

x +∆x

f(x +∆x) − f (x)

∆x

6x∆x + 5∆x + 3(∆x)

∆x

+ 6x∆x + 3(∆x)

+ 5x + 5∆x − 6 − 3x

− 5x + 6

∆x

[3(x +∆x)

+ 5(x +∆x) − 6] − [3x

+ 5x − 6]

∆x

f(x +∆x) − f (x)

∆x

MFE_Z01.qxd 16/12/2005 10:50 Page 589