Jacques I. Mathematics for Economics and Business
Подождите немного. Документ загружается.

MFE_C08b.qxd 16/12/2005 10:48 Page 550

chapter 9
Dynamics
This chapter provides a simple introduction to the dynamics of economic systems. So
far, all of our models have been static. We have implicitly assumed that equilibrium
prices and incomes are somehow attained instantaneously, as if by magic. In
practice, economic variables take time to vary. The incorporation of time into eco-
nomic models is known as dynamics and it enables us to decide whether equilibrium
values are actually achieved and, if so, exactly how individual variables approach
these values. There are two sections that can be read in either order.
In Section 9.1 we consider the case when time, t, is a discrete variable taking whole-
number values. This describes the situation in which variables change only after fixed
periods. For example, the prices of certain agricultural products change from one
season to the next but are fixed throughout each season. We express this time
dependence using an obvious subscript notation. The price during the first period
is denoted by P
1
, the price during the second period is P
2
, and so on. Equations
that relate the price in one period, P
t
, to that of the previous period, P
t−1
, are called
difference equations and a method is described for the solution of such equations.
In Section 9.2 we consider the case when time is a continuous variable taking all pos-
sible values in a certain interval. This describes the situation in which variables
change from one moment to the next. For example, the prices of certain commodi-
ties, such as oil, effectively change instantaneously and are not fixed on a seasonal
basis. We express this time dependence using the usual function notation, P(t). It is
appropriate to model the rate of change of P with respect to t using the derivative,
P′(t). Equations that involve the derivatives of an unknown function are called dif-
ferential equations and a method is described for solving such equations.
MFE_C09a.qxd 16/12/2005 10:49 Page 551

It is not possible in an introductory book such as this to give you more than a flavour
of the mathematics of dynamics. However, in spite of this, we show you how to
solve dynamic systems in both macroeconomics and microeconomics. Also, we hope
that this chapter will encourage you to read other books that describe more
advanced methods and models.
MFE_C09a.qxd 16/12/2005 10:49 Page 552

section 9.1
Difference equations
A difference equation (sometimes called a recurrence relation) is an equation that relates con-
secutive terms of a sequence of numbers. For example, the equation
Y
t
= 2Y
t−1
describes sequences in which one number is twice its predecessor. There are obviously many
sequences that satisfy this requirement, including
2, 4, 8, 16,...
5, 10, 20, 40,...
−1, −2, −4, −8,...
In order to determine the sequence uniquely, we need to be given some additional information,
such as the first term. It is conventional to write the first term as Y
0
, and once this is given a
specific value all remaining terms are known.
Objectives
At the end of this section you should be able to:
Find the complementary function of a difference equation.
Find the particular solution of a difference equation.
Analyse the stability of economic systems.
Solve lagged national income determination models.
Solve single-commodity-market models with lagged supply.
MFE_C09a.qxd 16/12/2005 10:49 Page 553

The following problem gives you an opportunity to solve difference equations for yourself.
Dynamics
554
Example
Write down the first four terms of the sequence defined by
Y
0
= 3 and Y
t
= 2Y
t−1
and obtain a formula for the general term Y
t
in terms of t.
Solution
If Y
0
= 3 then
Y
1
= 2Y
0
= 2 × 3 = 6
Y
2
= 2Y
1
= 2 × 6 = 12
Y
3
= 2Y
2
= 2 × 12 = 24
In order to produce a formula for the general term, we write these as
Y
1
= 2Y
0
= 2
1
× 3
Y
2
= 2Y
1
= 2
2
× 3
Y
3
= 2Y
2
= 2
3
× 3
It is now obvious from this pattern that the general term, given by
Y
t
= 3(2
t
)
is the solution of the difference equation
Y
t
= 2Y
t−1
with initial condition
Y
0
= 3
Practice Problem
1 Starting with the given initial conditions, write down the first four terms of each of the following
sequences. By expressing these as an appropriate power, write down a formula for the general term,
Y
t
in terms of t.
(1) (a)
Y
t
= 3Y
t−1
; Y
0
= 1 (b) Y
t
= 3Y
t−1
; Y
0
= 7 (c) Y
t
= 3Y
t−1
; Y
0
= A
(2) (a) Y
t
= Y
t−1
; Y
0
= 1 (b) Y
t
= Y
t−1
; Y
0
= 7 (c) Y
t
= Y
t−1
; Y
0
= A
(3) Y
t
= bY
t−1
; Y
0
= A
1
2
1
2
1
2
The result of the last part of Practice Problem 1 shows that the solution of the general equation
Y
t
= bY
t−1
(1)
with initial condition
MFE_C09a.qxd 16/12/2005 10:49 Page 554

Y
0
= A
is given by
Y
t
= A(b
t
)
Before we can consider the use of difference equations in economic models, we must exam-
ine the solution of more general equations of the form
Y
t
= bY
t−1
+ c (2)
where the right-hand side now includes a non-zero constant, c. We begin by defining some
terminology. The general solution of equation (2) can be written as the sum of two separate
expressions known as the complementary function (CF) and the particular solution (PS). The
complementary function is the name that we give to the solution of equation (2) when the con-
stant, c, is zero. In this case, equation (2) reduces to equation (1), and so
CF = A(b
t
)
The particular solution is the name that we give to any solution of equation (2) that we are
clever enough to ‘spot’. This turns out to be rather easier to do than might at first appear and
we will see how this can be done in a moment. Finally, once CF and PS have been found, we
can write down the general solution of equation (2) as
Y
t
= CF + PS = A(b
t
) + PS
A proof of this result can be found in Practice Problem 8 at the end of this section. The letter
A is no longer equal to the first term, Y
0
, although it can easily be calculated, as the following
example demonstrates.
9.1 • Difference equations
555
Example
Solve the following difference equations with the specified initial conditions. Comment on the qualitative
behaviour of the solution in each case.
(a) Y
t
= 4Y
t−1
+ 21; Y
0
= 1
(b) Y
t
= Y
t−1
+ 8; Y
0
= 2
Solution
(a) The difference equation
Y
t
= 4Y
t−1
+ 21
is of the standard form
Y
t
= bY
t−1
+ c
and so can be solved using the complementary function and particular solution. The complementary
function is the general solution of the equation when the constant term on the right-hand side is
replaced by zero: that is, it is the solution of
Y
t
= 4Y
t−1
which is A(4
t
).
The particular solution is any solution of the original equation
1
3
MFE_C09a.qxd 16/12/2005 10:49 Page 555
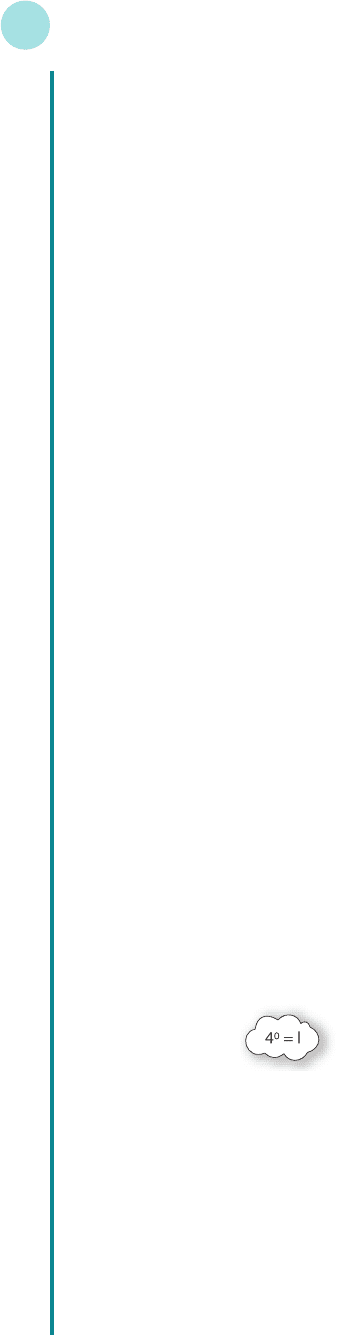
Y
t
= 4Y
t−1
+ 21
that we are able to find. In effect, we need to think of a sequence of numbers, Y
t
, such that when this is
substituted into
Y
t
− 4Y
t−1
we obtain the constant value of 21. One obvious sequence likely to work is a constant sequence,
Y
t
= D
for some number, D. If this is substituted into
Y
t
= 4Y
t−1
+ 21
we obtain
D = 4D + 21
(Note that Y
t
= D whatever the value of t so Y
t−1
is also equal to D.) This algebraic equation can be re-
arranged to get
−3D = 21
and so D =−7.
We have therefore shown that the complementary function is given by
CF = A(4
t
)
and that the particular solution is
PS =−7
Hence
Y
t
= CF + PS = A(4
t
) − 7
which is the general solution of the difference equation
Y
t
= 4Y
t−1
+ 21
To find the specific solution that satisfies the initial condition
Y
0
= 1
we simply put t = 0 in the general solution to get
Y
0
= A(4
0
) − 7 = 1
that is,
A − 7 = 1
which gives
A = 8
The solution is
Y
t
= 8(4
t
) − 7
A graphical interpretation of this solution is shown in Figure 9.1 where Y
t
is plotted against t. It is
tempting to join the points up with a smooth curve. However, this does not make sense because t is
allowed to take only whole-number values. Consequently, we join up the points with horizontal lines
to create the ‘staircase’ which more properly reflects the fact that t is discrete. Figure 9.1 shows that the
values of Y
t
increase without bound as t increases. This is also apparent from the formula for Y
t
because
Dynamics
556
MFE_C09a.qxd 16/12/2005 10:49 Page 556

the numbers 4
t
get ever larger as t increases. We describe this by saying that the time path diverges uni-
formly or explodes. This sort of behaviour can be expected to occur for any solution
Y
t
= A(b
t
) + PS
where b > 1.
(b) The difference equation
Y
t
= Y
t−1
+ 8
can be solved in a similar way to that of part (a). The complementary function is given by
CF = A
t
and for a particular solution we try
Y
t
= D
for some constant D. Substituting this into the difference equation gives
D = D + 8
which has solution D = 12, so
PS = 12
The general solution is therefore
Y
t
= CF + PS = A
t
+ 12
D
F
1
3
A
C
1
3
D
F
1
3
A
C
1
3
9.1 • Difference equations
557
Figure 9.1
MFE_C09a.qxd 16/12/2005 10:49 Page 557
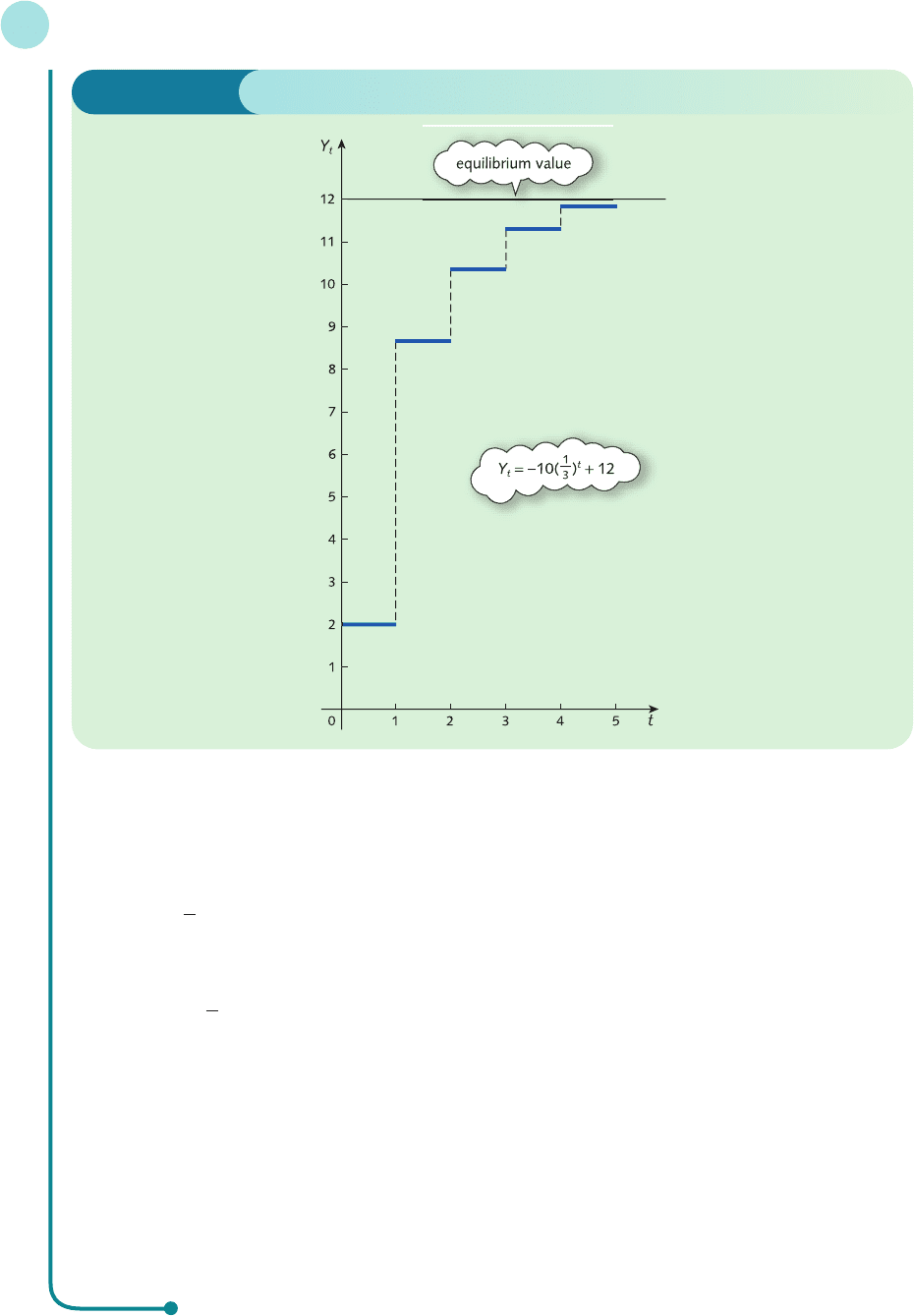
Finally, the specific value of A can be found from the initial condition
Y
0
= 2
Setting t = 0 in the general solution gives
2 = A
0
+ 12 = A + 12
and so A is −10. The solution is
Y
t
=−10
t
+ 12
This solution is sketched in Figure 9.2, which shows that the values of Y
t
increase but eventually settle
down at 12. We describe this by saying that the time path converges uniformly to the value of 12, which
is referred to as the equilibrium value. This behaviour is also apparent from the formula for Y
t
because
the number (1/3)
t
gets ever smaller as t increases. In effect, the complementary function disappears,
leaving just the particular solution. The particular solution is the equilibrium value of Y
t
whereas the
complementary function measures the deviation from the equilibrium which, in this case, converges to
zero as t increases. This sort of behaviour can be expected to occur for any solution
Y
t
= A(b
t
) + PS
when 0 < b < 1.
D
F
1
3
A
C
D
F
1
3
A
C
Dynamics
558
Figure 9.2
MFE_C09a.qxd 16/12/2005 10:49 Page 558
9.1 • Difference equations
559
Practice Problem
2 Solve the following difference equations with the specified initial conditions:
(a)
Y
t
=−
1
/2Y
t−1
+ 6; Y
0
= 0 (b) Y
t
=−2Y
t
+ 9; Y
0
= 4
In each case, sketch the corresponding ‘staircase’ diagram and comment on the qualitative behaviour
of the solution as t increases.
The results of the previous example and Practice Problem 2 can be summarized:
If b
>>
1 then Y
t
displays uniform divergence.
If 0
<<
b
<<
1 then Y
t
displays uniform convergence.
If
−−
1
<<
b
<<
0 then Y
t
displays oscillatory convergence.
If b
<< −−
1 then Y
t
displays oscillatory divergence.
The remaining possibilities, b = 1, b =−1 and b = 0, are considered in Practice Problem 6 at the
end of this section, which shows that Y
t
converges when b is 0 but diverges when b is 1 or −1.
We conclude that the solution of the difference equation eventually settles down to an equilib-
rium state only when b lies in the range −1 < b < 1.
If convergence does occur in an economic model, the model is said to be stable. If the vari-
ables diverge, it is said to be unstable.
We now investigate two applications of difference equations taken from macroeconomics
and microeconomics, respectively:
national income determination
supply and demand analysis.
We consider each of these in turn.
9.1.1 National income determination
In Section 1.6 we introduced a simple two-sector model with structural equations
Y = C + I
C = aY + b
I = I*
where b and I* denote autonomous consumption and investment, and a is the marginal
propensity to consume, which lies in the range 0 < a < 1. In writing down the equations in this
form, we are implicitly assuming that only one time period is involved, that consumption
depends on national income within this time period and that equilibrium values are attained
instantaneously. In practice, there is a time lag between consumption and national income.
Consumption, C
t
, in period t depends on national income, Y
t−1
, in the previous period, t − 1.
The corresponding consumption function is given by
C
t
= aY
t−1
+ b
MFE_C09a.qxd 16/12/2005 10:49 Page 559
