Jacques I. Mathematics for Economics and Business

Подождите немного. Документ загружается.

the contract. High-quality beef comes from two sources. Plant P1 processes 60 kg per day, whereas plant P2

processes 20 kg per day. Hence the total weekly output of high-quality beef is

60x + 20y

The contract is therefore satisﬁed provided

60x + 20y ≥ 120

A similar argument holds for both medium- and low-quality beef. The corresponding constraints are

20x + 20y ≥ 80

40x + 120y ≥ 240

Looking back, it is easy to check that every piece of numerical information has been used in the formula-

tion so far. However, there are still four further constraints to write down! These are based on common

sense, but they do need to be built into the statement of the linear programming problem. The number of

days in a week is 7, so the values of x and y must range between 0 and 7. Thus we have

x ≥ 0 and y ≥ 0

x ≤ 7 and y ≤ 7

The complete problem may now be stated:

Minimize 4000x + 3200y

subject to

60x + 20y ≥ 120

20x + 20y ≥ 80

40x + 120y ≥ 240

x ≤ 7

y ≤ 7

x ≥ 0

y ≥ 0

It can now be solved by applying the method described in Section 8.1.

Step 1

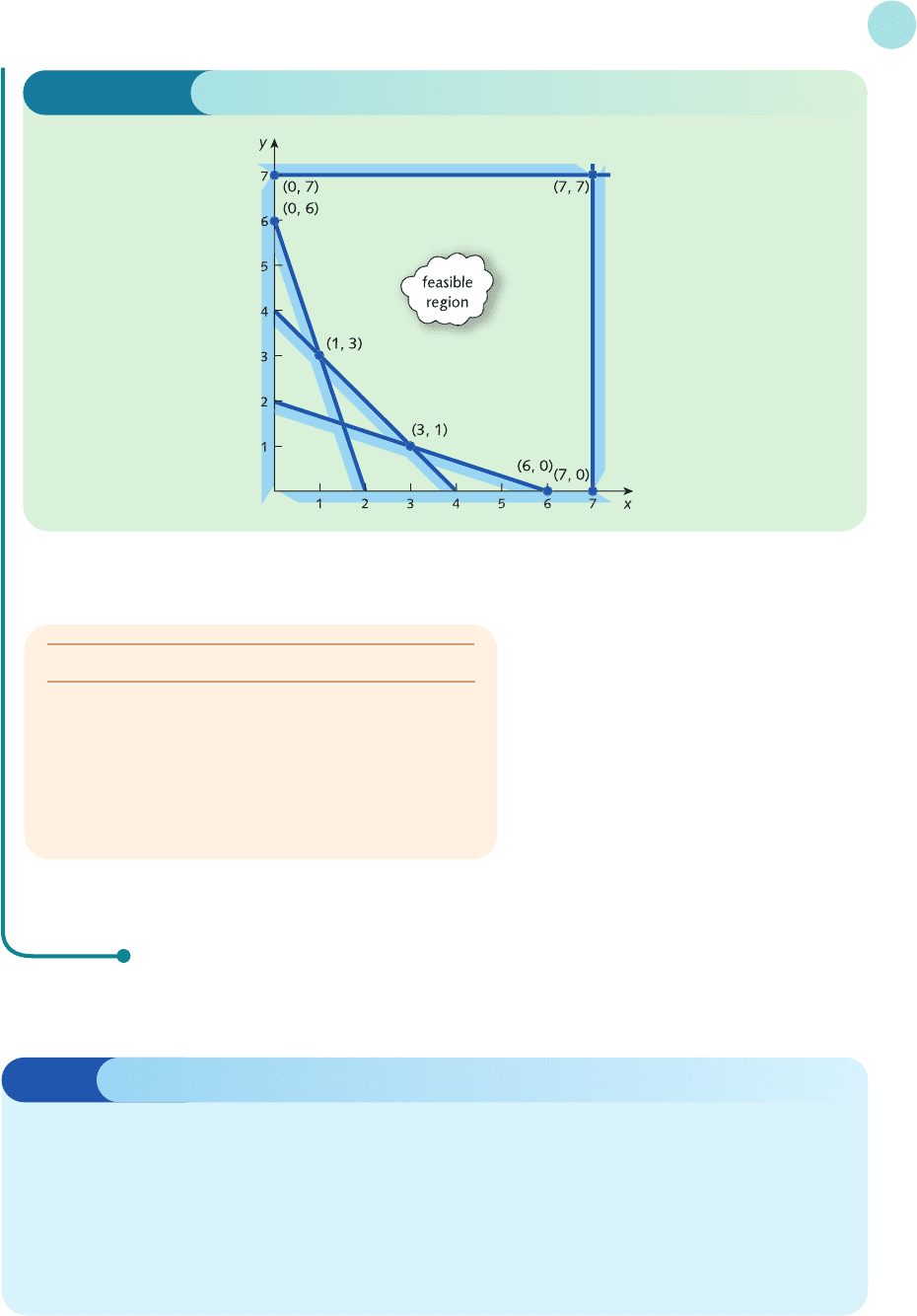
The feasible region can be sketched in the usual way. Note that the last four constraints merely indicate that

the region is boxed in by the vertical and horizontal lines x = 0, x = 7, y = 0 and y = 7.

The line 60x + 20y = 120 passes through (0, 6) and (2, 0).

The line 20x + 20y = 80 passes through (0, 4) and (4, 0).

The line 40x + 120y = 240 passes through (0, 2) and (6, 0).

Also the test point (0, 0) does not satisfy any of the ﬁrst three constraints, so the feasible region lies above

these lines, as shown in Figure 8.14.

Step 2

The feasible region has corners (7, 0), (7, 7), (0, 7), (1, 3), (3, 1), (0, 6) and (6, 0).

Linear Programming

540

MFE_C08b.qxd 16/12/2005 10:48 Page 540

Step 3

8.2 • Applications of linear programming

541

Figure 8.14

Corner Objective function

(7, 0) 28 000

(7, 7) 50 400

(0, 7) 22 400

(0, 6) 19 200

(3, 1) 15 200

(1, 3) 13 600

(6, 0) 24 000

The minimum cost is $13 600 and is obtained by operating plant P1 for 1 day a week and plant P2 for 3 days

a week.

Advice

Perhaps one of the more difficult aspects of formulating linear programming problems is

remembering to include the obvious constraints arising from common sense. In the previ-

ous example, the last four constraints are so obvious that it is all too easy to omit them,

particularly because they are not mentioned explicitly in the original specification. We

might therefore include the following point in our general strategy:

(4) Write down any obvious constraints, such as the non-negativity constraints, that you

may have forgotten about in (3).

MFE_C08b.qxd 16/12/2005 10:48 Page 541

Linear Programming

542

Practice Problem

2 A small publishing company decides to use one section of its plant to produce two textbooks called

Microeconomics and Macroeconomics. The profit made on each copy is $12 for Microeconomics

and $18 for Macroeconomics. Each copy of Microeconomics requires 12 minutes for printing and

18 minutes for binding. The corresponding figures for Macroeconomics are 15 and 9 minutes respec-

tively. There are 10 hours available for printing and 10

/2 hours available for binding. How many of

each should be produced to maximize profit?

Example

An insurance company employs full- and part-time staff, who work 40 and 20 hours per week respectively.

Full-time staff are paid $800 per week and part-time staff $320. In addition, it is company policy that the

number of part-time staff should not exceed one-third of the number of full-time staff.

If the number of worker-hours per week required to deal with the company’s work is 900, how many

workers of each type should be employed in order to complete the workload at minimum cost?

Solution

If the company employs x full-time staff and y part-time staff then the company would like to choose x

and y to minimize its weekly salary costs. Also, since full- and part-time staff are paid $800 and $320 per

week, respectively, the total wage bill is then

800x + 320y

which is the objective function that needs to be minimized.

Full- and part-time staff work 40 and 20 hours per week, respectively, so the total number of worker-

hours available is

40x + 20y

It is required that this is at least 900, so we obtain the constraint

40x + 20y ≥ 900

A further constraint on the company arises from the fact that the number of part-time staff cannot exceed

one-third of the number of full-time staff. This means, for example, that if the company employs 30 full-

time staff then it is not allowed to employ more than 10 part-time staff because

1/3 × 30 = 10

In general, if x denotes the number of full-time staff then the number of part-time staff, y, cannot exceed

x/3: that is,

y ≤ x/3

In addition, we have the obvious non-negativity constraints

x ≥ 0 and y ≥ 0

The complete problem may now be stated:

Minimize 800x + 320y

subject to

MFE_C08b.qxd 16/12/2005 10:48 Page 542

40x + 20y ≥ 900

y ≤ x/3

x ≥ 0

y ≥ 0

It can now be solved by applying the method described in Section 8.1.

Step 1

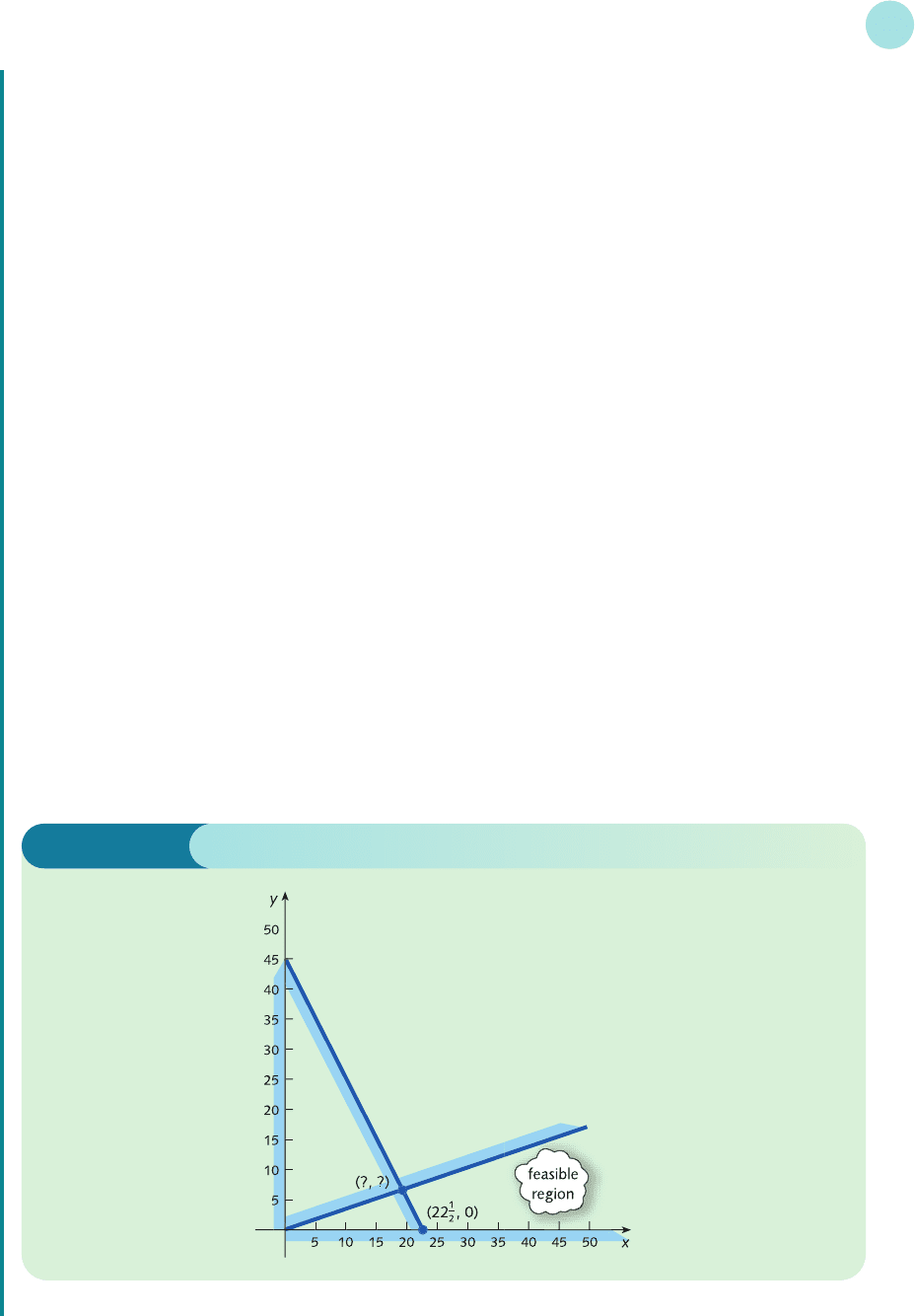
The feasible region can be sketched in the usual way. The line y = x/3 passes through (0, 0), (3, 1), (6, 2) and

so on. Unfortunately, because the origin actually lies on the line, it is necessary to use some other point as a

test point. For example, substituting x = 30, y = 5 into the inequality

y ≤ x/3

gives

5 ≤ (30)/3

This inequality is clearly true, indicating that (30, 5), which lies below the line, is in the region of interest.

The constraint

40x + 20y ≥ 900

is easier to handle. The corresponding line passes through (0, 45) and (22

2, 0), and using the origin as a test

point shows that we need to shade the region below the line. The feasible region is sketched in Figure 8.15.

Step 2

The feasible region has two corners. One of these is obviously (22

2, 0). However, it is not possible to write

down directly from the diagram the coordinates of the other corner. This is formed by the intersection of

the two lines

8.2 • Applications of linear programming

543



Figure 8.15

MFE_C08b.qxd 16/12/2005 10:48 Page 543

y = x/3 (1)

40x + 20y = 900 (2)

and so we must solve this system algebraically. In this case the easiest thing to do is to substitute equation

(1) into equation (2) to eliminate y immediately. This gives

40x + x = 900

that is,

x = 900

which has solution

x ===19

Finally, from equation (1),

y = x =× = =6

The feasible region therefore has coordinates (19

7, 6

7) and (22

2, 0).

Step 3

135

2700

140

Linear Programming

544

The minimum cost is $17 485.71, which occurs when x = 19

/7 and y = 6

/7.

It might appear that this is the solution to our original problem. This is certainly mathematically correct,

but it cannot possibly be the solution that we are looking for, since it does not make sense, for example, to

employ

/7 of a worker. We are only interested in points whose coordinates are whole numbers. A problem

such as this is referred to as an integer programming problem. We need to ﬁnd that point (x, y) inside the

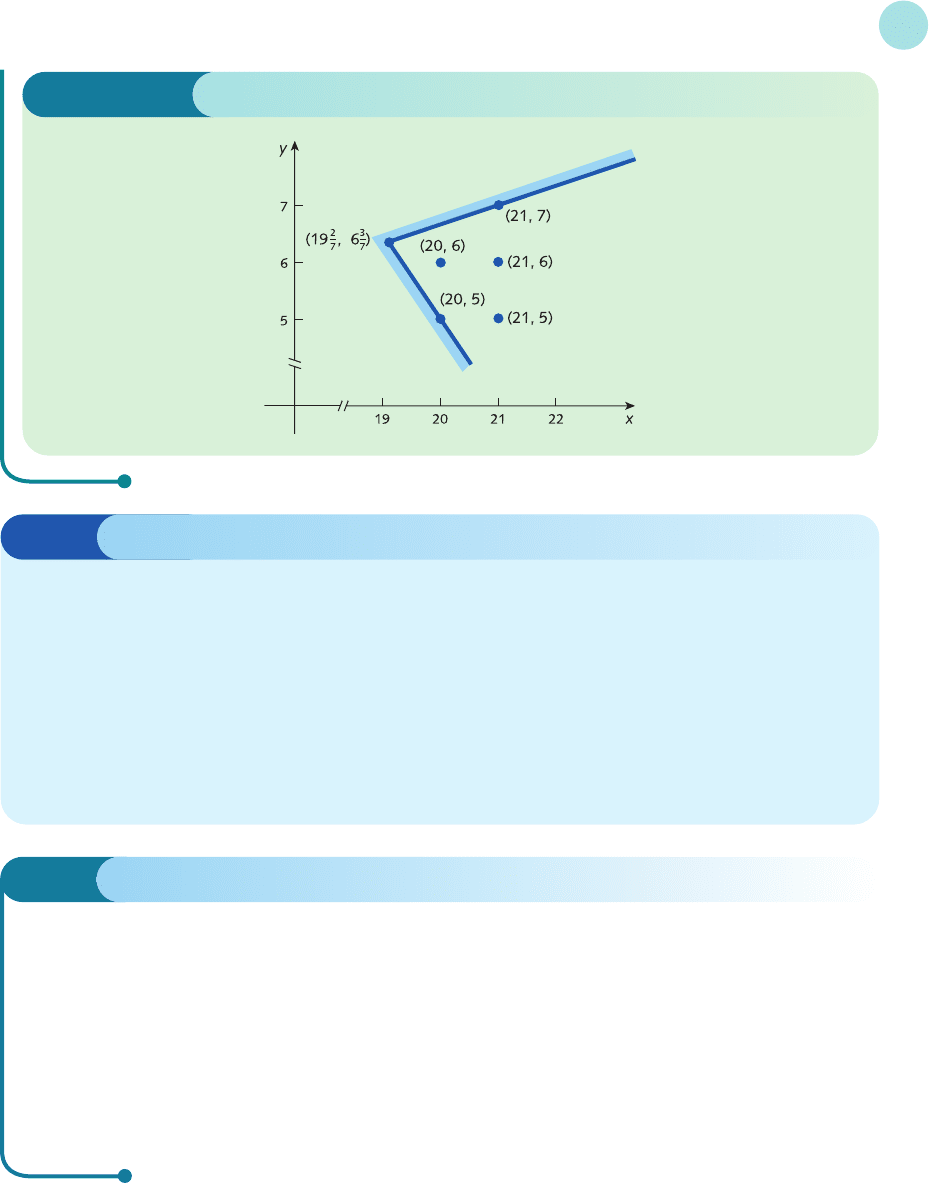
feasible region where both x and y are whole numbers which minimizes the objective function. A ‘blow-up’

picture of the feasible region near the minimum cost corner is shown in Figure 8.16, and the following table

indicates that the optimal solution is (20, 5).

Other points in the neighbourhood with whole-number coordinates are (20, 6), (20, 7), (21, 5) and so on.

However, all of these have either a larger value of x or a larger value of y (or both) and so must produce

a larger total cost. The company should therefore employ 20 full- and 5 part-time staff to minimize its

salary bill.

Corner Objective function

(19

7, 6

7)17485

(22

/2, 0) 18 000

Corner Objective function

(20, 5) 17 600

(20, 6) 17 920

(21, 5) 18 400

(21, 6) 18 720

MFE_C08b.qxd 16/12/2005 10:48 Page 544

In this section we have described how to formulate linear programming problems. The

general strategy may be summarized:

(1) Identify the unknowns and label them x and y.

(2) Write down an expression for the objective function in terms of x and y, and decide

whether it needs maximizing or minimizing.

8.2 • Applications of linear programming

545

Figure 8.16

Advice

This example highlights the need to look back at the original problem to make sure that

the final answer makes sense. It is very tempting when solving linear programming prob-

lems just to write down the solution without thinking, neatly underline it and then go on

to another problem. Unfortunately, it is all to easy to make mistakes, both in the problem

formulation and in sketching the feasible region. Spending a few moments checking the

validity of your solution may well help you to discover any blunders that you have made,

as well as suggesting possible modifications to the solution procedure, as in the previous

example. We might, therefore, conclude the general strategy with the following step:

(5) Check that the final answer makes sense as a solution to the original problem.

Practice Problem

3 An individual spends 95% of earned income on essential goods and services, leaving only 5% to be

spent on luxury goods, which is subdivided between trendy clothes and visits to the theatre. The

cost of each item of clothing is $150 and a trip to the theatre costs $70. The corresponding utility

function is

U = 3x + 7y

where x and y denote the number of trendy clothes and theatre visits per year, respectively. In order

to maintain a reasonable appearance throughout the year, it is vital that at least nine new items of

clothing are purchased each year. Given that annual earned income is $42 000, find the values of

x and y which maximize utility.

MFE_C08b.qxd 16/12/2005 10:48 Page 545

(3) Write down all constraints on the variables x and y.

(4) Write down any obvious constraints, such as the non-negativity constraints, that you may

have forgotten about in (3).

(5) Check that the ﬁnal answer makes sense as a solution to the original problem.

Obviously it is not essential that you follow this approach, although you may wish to refer to it

if you get stuck.

We conclude this section by showing how Maple can be used to solve linear programming

problems. This uses the simplex algorithm and can cope with problems involving more than

two unknowns. It is not necessary for you to understand what the simplex algorithm is to use

Maple. However, if you are interested, you might like to consult an academic textbook on

Discrete (sometimes called Decision) Mathematics.

Linear Programming

546

Example

A manufacturer produces three types of camera, X, Y and Z. Camera X requires 4 hours of staff time, 5 units

of raw materials and 1 machine-hour to produce. The corresponding ﬁgures for camera Y are 3, 9 and 1,

respectively. For Z, the ﬁgures are 3, 6 and 4, respectively. The proﬁts earned from the sale of each camera

of type X, Y and Z are $400, $300 and $250, respectively. The total number of staff-hours available is 800,

the number of units of raw materials available is 1100, and the number of machine-hours available is 400.

In addition, because of limited demand, it is decided that no more than 100 cameras of any one type should

be produced. How should the manufacturer arrange production to maximize proﬁt?

Solution

In this problem a decision needs to be made about the number of each type of camera to produce. We shall

denote these unknowns by x, y and z. The objective is to maximize proﬁt, so we type

>profit:=400*x+300*y+250*z;

The next thing to do is to input the constraints. Production levels are limited by staff-hours, raw materials,

machine-hours and demand. We consider each of these in turn and label the constraints c1, c2, c3 and

so on:

>c1:=4*x+3*y+3*z<=800;

>c2:=5*x+9*y+6*z<=1100;

>c3:=x+y+4*z<=400;

>c4:=x<=100;

>c5:=y<=100;

>c6:=z<=100;

Maple has many routines based on the simplex method, which we load by typing

>with(simplex):

We are ﬁnally in a position to solve the problem, which we do by typing:

MAPLE

MFE_C08b.qxd 16/12/2005 10:48 Page 546

8.2 • Applications of linear programming

547

which gives

{x=52, y=100, z=62}

Proﬁt is maximized by making 52 cameras of type X, 100 of type Y and 62 of type Z. The value of the proﬁt

itself can be found by typing

>subs({x=52,y=100,z=62},profit);

which gives $66 300.

>maximize(profit,{c1,c2,c3,c4,c5,c6},NONNEGATIVE);

Integer programming A linear programming problem in which the search for solution is

restricted to points in the feasible region with whole-number coordinates.

Key Terms

Practice Problems

4 A manufacturer produces two models of racing bike, B and C, each of which must be processed

through two machine shops. Machine shop 1 is available for 120 hours per month and machine shop

2 for 180 hours per month. The manufacture of each bike of type B takes 6 hours in shop 1 and

3 hours in shop 2. The corresponding times for C are 4 and 10 hours, respectively. If the profit is

$180 and $220 per bike of type B and C respectively, how should the manufacturer arrange produc-

tion to maximize total profit?

5 A small firm manufactures and sells litre cartons of non-alcoholic cocktails, ‘The Caribbean’ and ‘Mr

Fruity’, which sell for $1 and $1.25, respectively. Each is made by mixing fresh orange, pineapple

and apple juices in different proportions. The Caribbean consists of 1 part orange, 6 parts pineapple

and 1 part apple. Mr Fruity consists of 2 parts orange, 3 parts pineapple and 1 part apple. The firm

can buy up to 300 litres of orange juice, up to 1125 litres of pineapple juice and up to 195 litres of

apple juice each week at a cost of $0.72, $0.64 and $0.48 per litre, respectively.

Find the number of cartons of ‘The Caribbean’ and ‘Mr Fruity’ that the firm should produce to max-

imize profits. You may assume that non-alcoholic cocktails are so popular that the firm can sell all that

it produces.

6 In a student’s diet a meal consists of beefburgers and chips. Beefburgers have 1 unit of nutrient N1,

4 units of N2 and 125 calories per ounce. The figures for chips are

/2 unit of N1, 1 unit of N2 and

60 calories per ounce. In the interests of the student’s health it is essential for the meal to contain at

least 7 units of N1 and 22 units of N2.



MFE_C08b.qxd 16/12/2005 10:48 Page 547

What should the student ask for on the next visit to the refectory to satisfy the nutrient require-

ments and minimize the number of calories?

7 A manufacturer of outdoor clothing makes wax jackets and trousers. Each jacket requires 1 hour to

make, whereas each pair of trousers takes 40 minutes. The materials for a jacket cost $32 and those

for a pair of trousers cost $40. The company can devote only 34 hours per week to the production

of jackets and trousers, and the firm’s total weekly cost for materials must not exceed $1200. The

company sells the jackets at a profit of $12 each and the trousers at a profit of $14 per pair. Market

research indicates that the firm can sell all of the jackets that are produced, but that it can sell at most

half as many pairs of trousers as jackets.

(a) How many jackets and trousers should the firm produce each week to maximize profit?

(b) Due to the changes in demand, the company has to change its profit margin on a pair of trousers.

Assuming that the profit margin on a jacket remains at $12 and the manufacturing constraints

are unchanged, find the minimum and maximum profit margins on a pair of trousers which the

company can allow before it should change its strategy for optimum output.

8 A farmer wishes to feed pigs with minimum cost but needs to ensure that each receives at least

1.6 kg of protein, at least 0.3 kg of amino acid and no more than 0.3 kg of calcium per day. Foods

available are fish meal and meat scraps, which contain protein, calcium and amino acid according to

the following table:

Linear Programming

548

Kg protein Kg calcium Kg amino acid

per kg feed per kg feed per kg feed

Fish meal 0.60 0.05 0.18

Meat scraps 0.50 0.11 0.05

Fish meal costs $0.65 per kg, whereas meat scraps cost $0.52 per kg. Determine a minimum-cost

feeding programme.

9 (Maple) A firm allocates resources L, K and R to the production of three goods X, Y and Z. The

following table gives the amount of each input required to produce 1 unit of the given output:

The value of each unit of output is $10, $5 and $8 for X, Y and Z.

The resources available are 480, 300 and 180 for L, K and R.

Find the optimal resource allocation that maximizes the value of the total output.

10 (Maple) A farmer has two fields, the more fertile of which is 1400 hectares, the area of the other

being 800 hectares. She grazes cattle and grows barley by fencing off areas in both fields. Some of

the barley is kept for feed in the winter months. The profit per hectare is given by this table:

Output

XY Z

L 23 4

Input K 15 2

R 21 1

MFE_C08b.qxd 16/12/2005 10:48 Page 548

For winter feed alone she must allocate 1 hectare to barley for every 2 hectares allocated to cattle.

Also the farmer finds that she cannot increase the area allocated to cattle by more than 20% from

one year to the next.

Show that this can be formulated as a linear programming problem involving 8 unknowns and

15 constraints. Use the simplex method to solve this problem.

8.2 • Applications of linear programming

549

Year 1

Large field Small field

Barley $400 $220

Cattle $350 $200

Year 2

Large field Small field

Barley $420 $240

Cattle $540 $320

MFE_C08b.qxd 16/12/2005 10:48 Page 549