Jacques I. Mathematics for Economics and Business

Подождите немного. Документ загружается.

is needed if the solution is to be pinned down uniquely. This is usually provided in the form of

an initial condition in which we specify the value of K at t = 0. For example, the capital stock

may be known to be 500 initially. Substituting t = 0 into the general solution

K(t) =+c

gives

K(0) =+c = 500

and so c is 500. Hence the solution is

K(t) =+500

In this section we investigate more complicated differential equations such as

= 5y and =−y + 3

The right-hand sides of these equations are given in terms of y rather than t and cannot be

solved by direct integration. It turns out that the solution of such equations involves the expon-

ential function, e

which was ﬁrst introduced in Section 2.4. The letter e denotes the number

2.718 28...

and so e

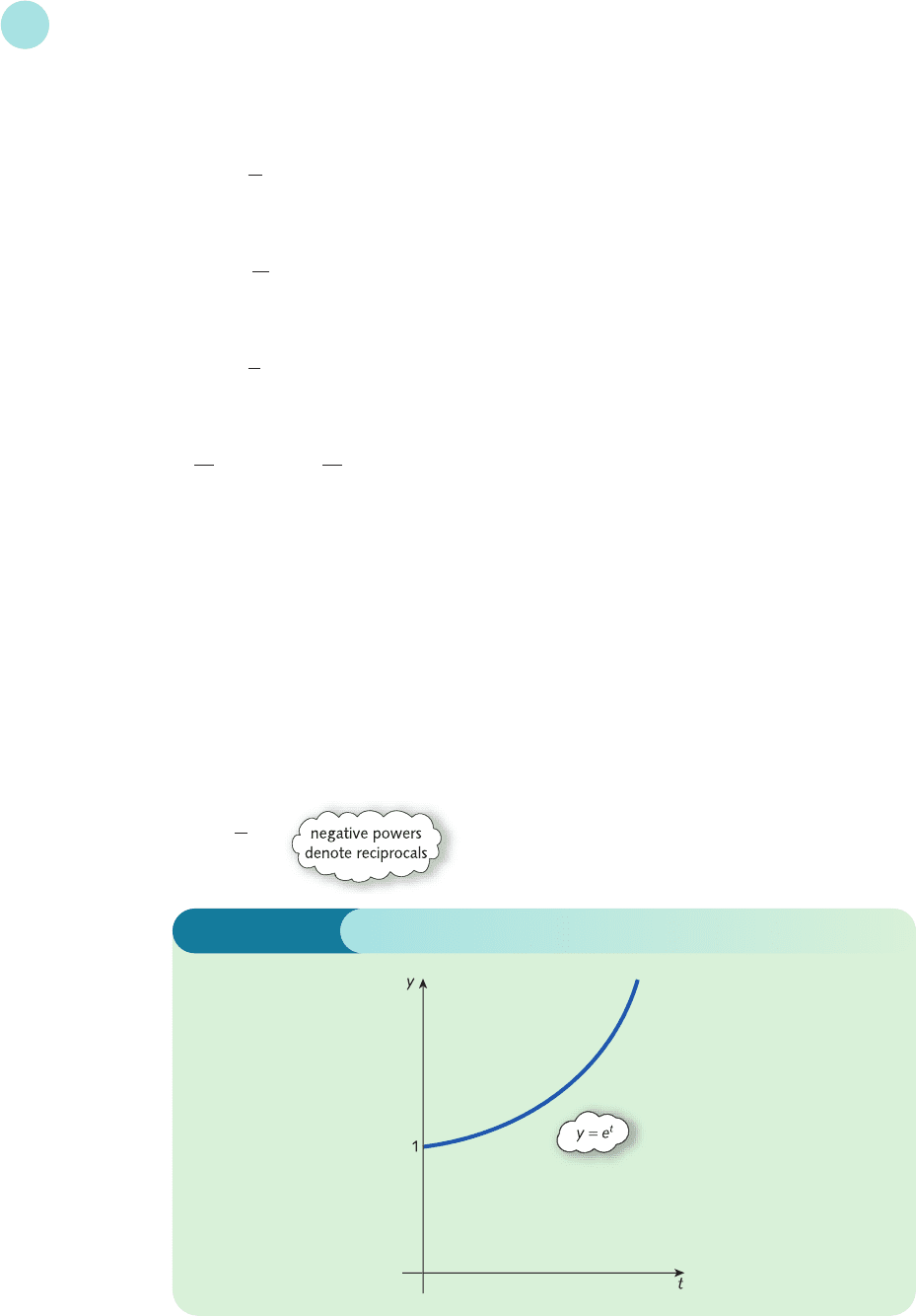
simply means 2.718 28...raised to the power of t. A graph of e

against t is sketched

in Figure 9.5, which shows that e

grows rapidly with rising t. In fact, the basic shape is the same

for all exponential functions of the form

y = e

when m is a positive constant. Figure 9.6 shows the graph of the negative exponential function,

−t

. The general behaviour of this function is to be expected because

−t

Dynamics

570

Figure 9.5

MFE_C09b.qxd 16/12/2005 10:49 Page 570

and, as t increases, the denominator increases, causing e

−t

to converge to zero. The basic shape

illustrated in Figure 9.6 is the same for all exponential functions of the form

y = e

when m is a negative constant.

The most important property of the exponential function is that it differentiates to itself:

that is,

if y = e

then = e

9.2 • Differential equations

571

Figure 9.6

Example

Write down expressions for in the case when

(a) y = e

(b) y = 7e

−4t

− 9

Solution

In Section 4.8 we showed that:

if y = e

then = me

so that e

differentiates to m times itself.

Applying this result to

(a) y = e

gives = 3e

(b) y = 7e

−4t

− 9 gives =−28e

−4t

MFE_C09b.qxd 16/12/2005 10:49 Page 571

Dynamics

572

Practice Problem

1 Write down expressions for in the case when

(a)

y = e

(b) y = 2e

−3t

Example

Find the solution of the differential equation

= 3y

which satisﬁes the initial condition, y(0) = 5.

Solution

The solution of the equation

= 3y

is any function, y(t), which differentiates to three times itself. We have noted that e

differentiates to m

times itself, so an obvious candidate for the solution is

y = e

However, there are many functions with the same property, including

y = 2e

, y = 5e

and y =−7.52e

Indeed, any function of the form

y = Ae

satisﬁes this differential equation because

= 3(Ae

) = 3y

The precise value of the constant A is determined from the initial condition

y(0) = 5

If we substitute t = 0 into the general solution

y(t) = Ae

we get

y(0) = Ae

= A

and so A is 5. The solution is

y(t) = 5e

MFE_C09b.qxd 16/12/2005 10:49 Page 572

Consider the differential equation

= my + c (1)

where m and c are constants. The general solution of equation (1) is the sum of two separate

functions, known as the complementary function (CF) and particular solution (PS). These

are deﬁned in much the same way as their counterparts for difference equations discussed in

the previous section. The complementary function is the solution of equation (1) when the

constant term on the right-hand side is replaced by zero. In other words, the complementary

function is the solution of

= my

The results of Practice Problem 2 show that this is given by

CF = Ae

The particular solution is any solution that we are able to ﬁnd of the original equation (1). This

can be done by ‘guesswork’, just as we did in Section 9.1. Finally, once CF and PS have been

determined, the general solution of equation (1) can be written down as

y = CF + PS = Ae

+ PS

As usual, the speciﬁc value of A can be worked out at the very end of the calculations via an

initial condition.

9.2 • Differential equations

573

Practice Problem

2 (a) Find the solution of the differential equation

= 4y

which satisfies the initial condition, y(0) = 6.

(b) Find the solution of the differential equation

=−5y

which satisfies the initial condition, y(0) = 2.

Example

Solve the differential equation

=−2y + 100

in the case when the initial condition is

(a) y(0) = 10 (b) y(0) = 90 (c) y(0) = 50

Comment on the qualitative behaviour of the solution in each case.



MFE_C09b.qxd 16/12/2005 10:49 Page 573

Solution

The differential equation

=−2y + 100

is of the standard form

= my + c

and so can be solved using the complementary function and particular solution.

The complementary function is the general solution of the equation when the constant term is taken to

be zero: that is, it is the solution of

=−2y

which is Ae

−2t

. The particular solution is any solution of the original equation

=−2y + 100

that we are able to ﬁnd. In effect, we need to think of a function, y(t), such that when it is substituted into

+ 2y

we obtain the constant value of 100. One obvious function likely to work is a constant function,

y(t) = D

for some constant D. If this is substituted into

=−2y + 100

we obtain

0 =−2D + 100

(Note that dy/dt = 0 because constants differentiate to zero.) This algebraic equation can be rearranged

to get

2D = 100

and so D = 50.

We have therefore shown that the complementary function is given by

CF = Ae

−2t

and that the particular solution is

PS = 50

Hence

y(t) = CF + PS = Ae

−2t

+ 50

This is the general solution of the differential equation

=−2y + 100

Dynamics

574

MFE_C09b.qxd 16/12/2005 10:49 Page 574

(a) To ﬁnd the speciﬁc solution that satisﬁes the initial condition

y(0) = 10

we simply put t = 0 into the general solution to get

y(0) = Ae

+ 50 = 10

that is

A + 50 = 10

which gives

A =−40

The solution is

y(t) =−40e

−2t

+ 50

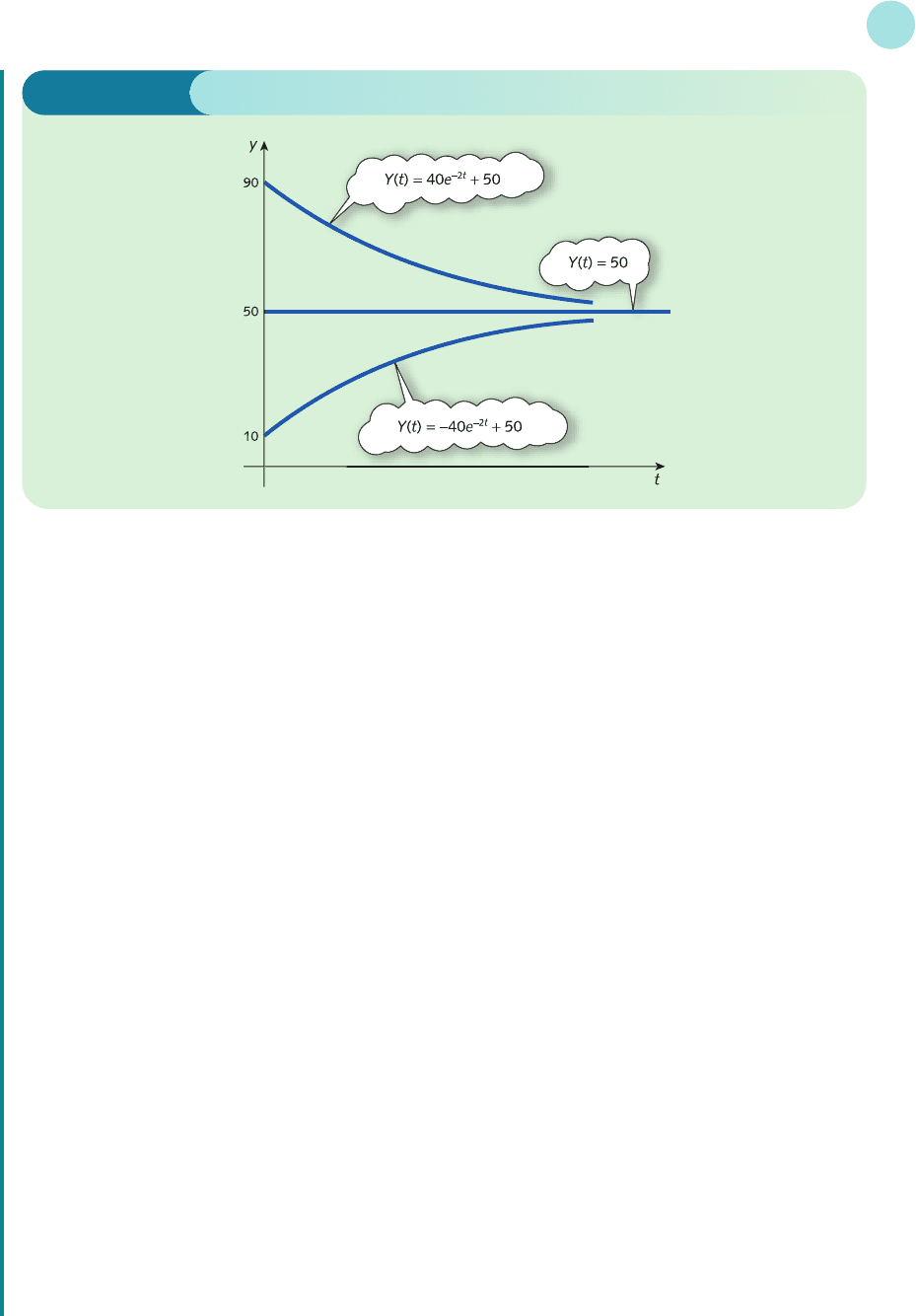
A graph of y against t is sketched as the bottom graph in Figure 9.7. This shows that y(t) increases from

its initial value of 10 and settles down at the value of 50 for sufﬁciently large t. As usual, this limit is

called the equilibrium value and is equal to the particular solution. The complementary function mea-

sures the deviation from the equilibrium.

(b) If the initial condition is

y(0) = 90

then we can substitute t = 0 into the general solution

y(t) = Ae

−2t

+ 50

to get

y(0) = Ae

+ 50 = 90

which has solution A = 40. Hence

y(t) = 40e

−2t

+ 50

9.2 • Differential equations

575

Figure 9.7



MFE_C09b.qxd 16/12/2005 10:49 Page 575

A graph of y against t is sketched as the top curve in Figure 9.7. In this case y(t) decreases from its

initial value of 90 but again settles down at the equilibrium level of 50.

y(0) = 50

then we can substitute t = 0 into the general solution

y(t) = Ae

−2t

+ 50

to get

y(0) = Ae

+ 50 = 50

which has solution A = 0. Hence

y(t) = 50

A graph of y against t is sketched as the horizontal line in Figure 9.7. In this case y is initially equal to

the equilibrium value and y remains at this constant value for all time.

Notice that the solution y(t) eventually settles down at the equilibrium value irrespective of the

initial conditions. This is because the coefﬁcient of t in the expression

CF = Ae

−2t

is negative, causing CF to converge to zero as t increases. We would expect convergence to occur for any

solution

y(t) = Ae

+ D

when m < 0.

Dynamics

576

Practice Problem

3 Solve the following differential equation subject to the given initial condition. Comment on the qualita-

tive behaviour of the solution as t increases.

= 3y − 60; y(0) = 30

The results of the previous example and Practice Problem 3 can be summarized as:

 if m < 0 then y(t) converges

 if m > 0 then y(t) diverges.

We say that an economic model is stable whenever the variables converge as t increases.

The above results indicate that an economic system represented by

= my + c

is stable if the coefﬁcient of y is negative and unstable if it is positive. Of course, it could

happen that m is zero. The differential equation then becomes

MFE_C09b.qxd 16/12/2005 10:49 Page 576

= c

which can be integrated directly to get

y(t) =



cdt = ct + d

for some arbitrary constant d. The corresponding model is therefore unstable unless c is also

zero, in which case y(t) takes the constant value of d for all t.

We now investigate two applications of differential equations taken from macroeconomics

and microeconomics respectively:

 national income determination

 supply and demand analysis.

We consider each of these in turn.

9.2.1 National income determination

The deﬁning equations of the usual two-sector model are

Y = C + I (1)

C = aY + b (2)

I = I* (3)

The ﬁrst of these is simply a statement that the economy is already in balance. The left-hand

side of equation (1) is the ﬂow of money from ﬁrms to households given as payment for the

factors of production. The right-hand side is the total ﬂow of money received by ﬁrms, either

in the form of investment, or as payment for goods bought by households. In practice, the

equilibrium values are not immediately attained and we need to make an alternative assump-

tion about how national income varies with time. It seems reasonable to suppose that the rate

of change of Y is proportional to the excess expenditure, C + I − Y: that is,

=α(C + I − Y ) (1′)

for some positive adjustment coefﬁcient, α. This makes sense because

 if C + I > Y, it gives dY/dt > 0 and so Y rises in order to achieve a balance between expendi-

ture and income

 if C + I = Y, it gives dY/dt = 0 and so Y is held constant at the equilibrium level

 if C + I < Y, it gives dY/dt < 0 and so Y falls in order to achieve a balance between expendi-

ture and income.

The usual relations (2) and (3) can be substituted into the new equation (1′) to obtain

=α(aY + b + I* − Y )

=α(a − 1)Y +α(b + I*)

which we recognize as a differential equation of the standard form given in this section.

9.2 • Differential equations

577

MFE_C09b.qxd 16/12/2005 10:49 Page 577

Dynamics

578

Example

Consider the two-sector model

= 0.5(C + I − Y )

C = 0.8Y + 400

I = 600

Find an expression for Y(t) when Y(0) = 7000. Is this system stable or unstable?

Solution

Substituting the expressions for C and I into

= 0.5(C + I − Y )

gives

= 0.5(0.8Y + 400 + 600 − Y )

=−0.1Y + 500

The complementary function is given by

CF = Ae

−0.1t

and for a particular solution we try

Y(t) = D

for some constant, D. Substituting this into the differential equation gives

0 =−0.1D + 500

which has solution D = 5000. The general solution is therefore

Y(t) = Ae

−0.1t

+ 5000

The initial condition

Y(0) = 7000

gives

A + 5000 = 7000

and so A is 2000. The solution is

Y(t) = 2000e

−0.1t

+ 5000

The ﬁrst term is a negative exponential, so it converges to zero as t increases. Consequently, Y(t) eventually

settles down to an equilibrium value of 5000 and the system is stable.

MFE_C09b.qxd 16/12/2005 10:49 Page 578

In the previous example and again in Practice Problem 4 we noted that the macroeconomic

system is stable. If we return to the general equation

=α(a − 1)Y +α(b + I*)

it is easy to see that this is always the case for the simple two-sector model, since the coefﬁcient

of Y is negative. This follows because, as previously stated, α>0 and because the marginal

propensity to consume, a, is less than 1.

9.2.2 Supply and demand analysis

The equations deﬁning the usual linear single-commodity market model are

= aP − b (1)

=−cP + d (2)

for some positive constants a, b, c and d. As in Section 9.1, we have written Q in terms of P for

convenience. Previously, we have calculated the equilibrium price and quantity simply by

equating supply and demand: that is, by putting

= Q

In writing down this relation, we are implicitly assuming that equilibrium is immediately

attained and, in doing so, we fail to take into account the way in which this is achieved. A

reasonable assumption to make is that the rate of change of price is proportional to excess

demand, Q

− Q

: that is,

=α(Q

− Q

) (3)

for some positive adjustment coefﬁcient, α. This makes sense because

 if Q

> Q

it gives dP/dt > 0 and so P increases in order to achieve a balance between supply

and demand

 if Q

= Q

it gives dP/dt = 0 and so P is held constant at the equilibrium level

 if Q

< Q

it gives dP/dt < 0 and so P decreases in order to achieve a balance between supply

and demand.

Substituting equations (1) and (2) into equation (3) gives

=α[(−cP + d) − (aP − b)] =−α(a + c)P +α(d + b)

which is a differential equation of the standard form.

9.2 • Differential equations

579

Practice Problem

4 Consider the two-sector model

= 0.1(C + I − Y )

C = 0.9Y + 100

I = 300

Find an expression for Y(t) when Y(0) = 2000. Is this system stable or unstable?

MFE_C09b.qxd 16/12/2005 10:49 Page 579