Jacques I. Mathematics for Economics and Business
Подождите немного. Документ загружается.

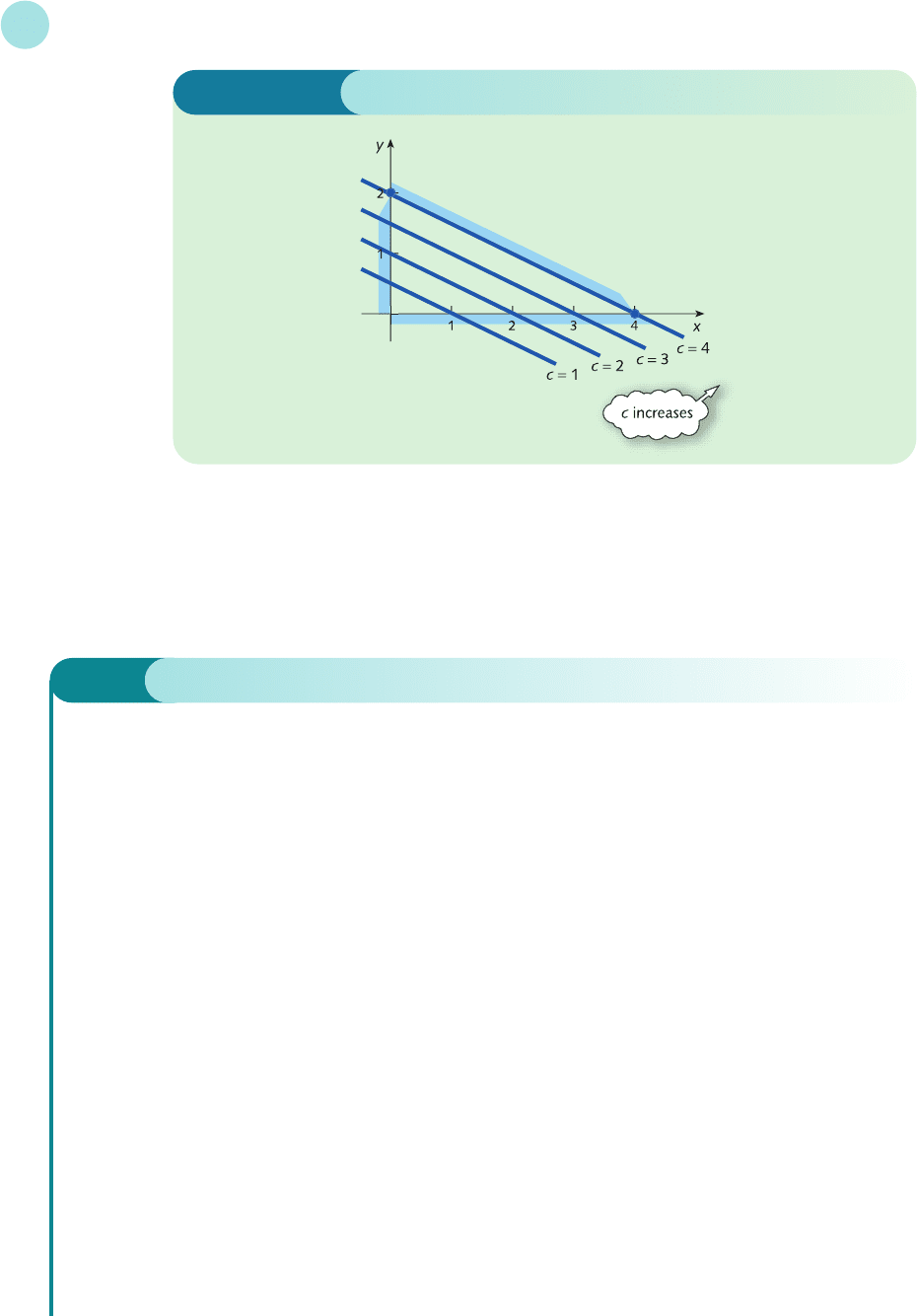
This example suggests the general result. If, in step 3, the maximum (or minimum) occurs
at two corners then the problem has infinitely many solutions. Any point on the line segment
joining these corners, including the two corners themselves, is also a solution.
Linear Programming
530
Figure 8.10
Example
Solve the linear programming problem
Maximize 3x + 2y
subject to
x + 4y ≥ 8
x + y ≥ 5
2x + y ≥ 6
x ≥ 0
y ≥ 0
What can you say about the solution if this problem is one of minimization rather than maximization?
Solution
Step 1
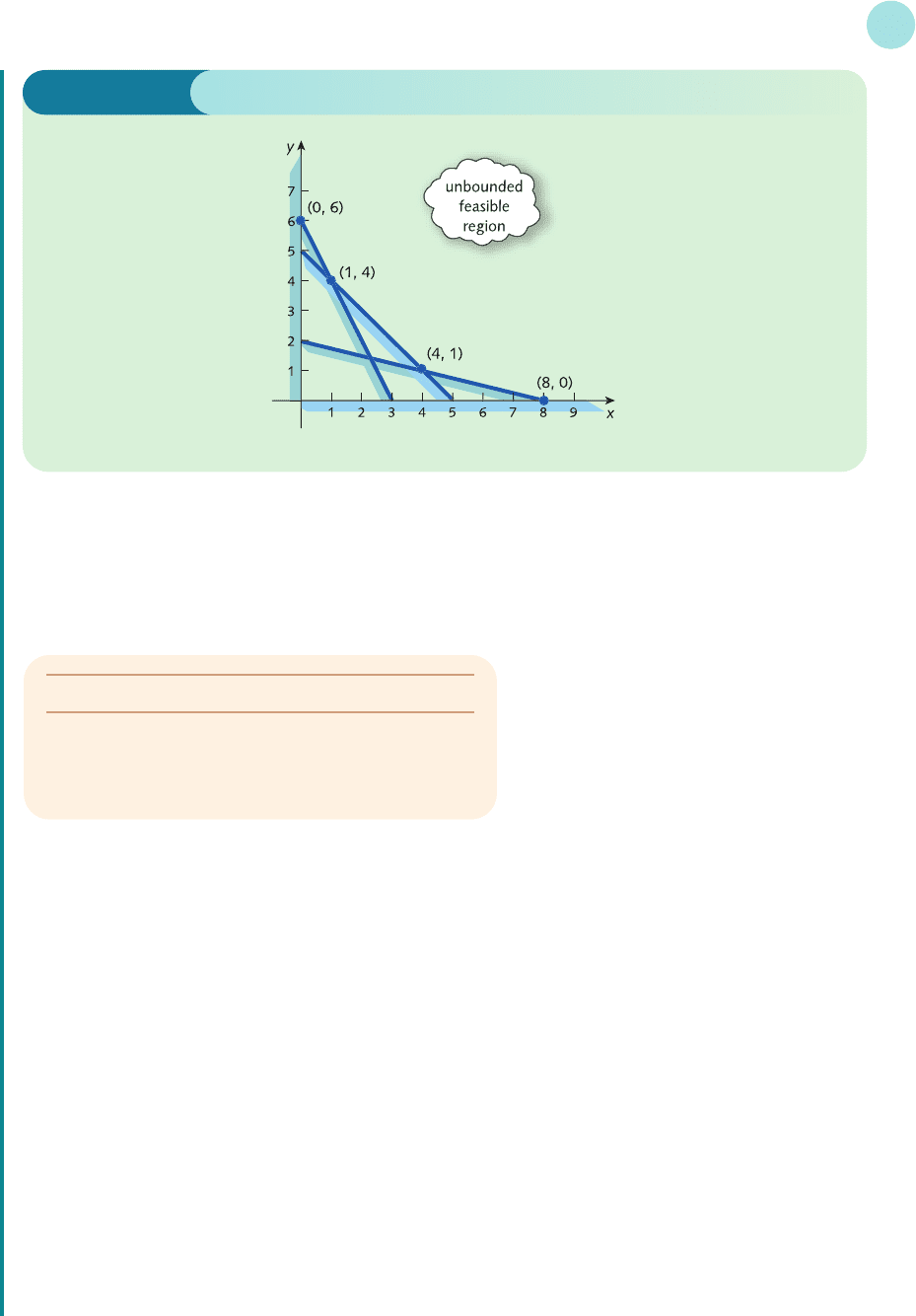
As usual the non-negativity constraints indicate that we need only consider the positive quadrant.
The line x + 4y = 8 passes through (0, 2) and (8, 0).
The line x + y = 5 passes through (0, 5) and (5, 0).
The line 2x + y = 6 passes through (0, 6) and (3, 0).
Also, the test point (0, 0) does not satisfy any of the corresponding constraints because the three inequality
signs are all ‘≥’. We are therefore interested in the region above all of these lines, as shown in Figure 8.11.
MFE_C08a.qxd 16/12/2005 10:47 Page 530
Step 2
The feasible region has four corners, (0, 6), (1, 4), (4, 1) and (8, 0).
Step 3
8.1 • Graphical solution of linear programming problems
531
Figure 8.11
Corner Objective function
(0, 6) 3(0) + 2(6) = 12
(1, 4) 3(1) + 2(4) = 11
(4, 1) 3(4) + 2(1) = 14
(8, 0) 3(8) + 2(0) = 24
From the table, the minimum and maximum values of the objective function are 11 and 24, which occur at
(1, 4) and (8, 0) respectively. However, we do have a slightly unusual situation in that the feasible region is
not enclosed on all sides. We describe this by saying that the feasible region is unbounded. It is open at the
top and, strictly speaking, it does not make sense to talk about the corners of such a region. Are we there-
fore justified in applying the ‘easy’ method in this case? To answer this question we superimpose the family
of lines
3x + 2y = c
representing the objective function, as shown in Figure 8.12 (overleaf ).
When c = 11 the line intersects the region at only one point (1, 4). However, as c increases from this value,
the lines sweep across the feasible region and never leave it, no matter how large c becomes. Consequently,
if the problem is one of maximization we conclude that it does not have a finite solution. We can substitute
huge values of x and y into 3x + 2y and get an ever-increasing result. On the other hand, if the problem is
one of minimization then it does have a solution at the corner (1, 4). This, of course, is the answer obtained
previously using the ‘easy’ method.
MFE_C08a.qxd 16/12/2005 10:47 Page 531
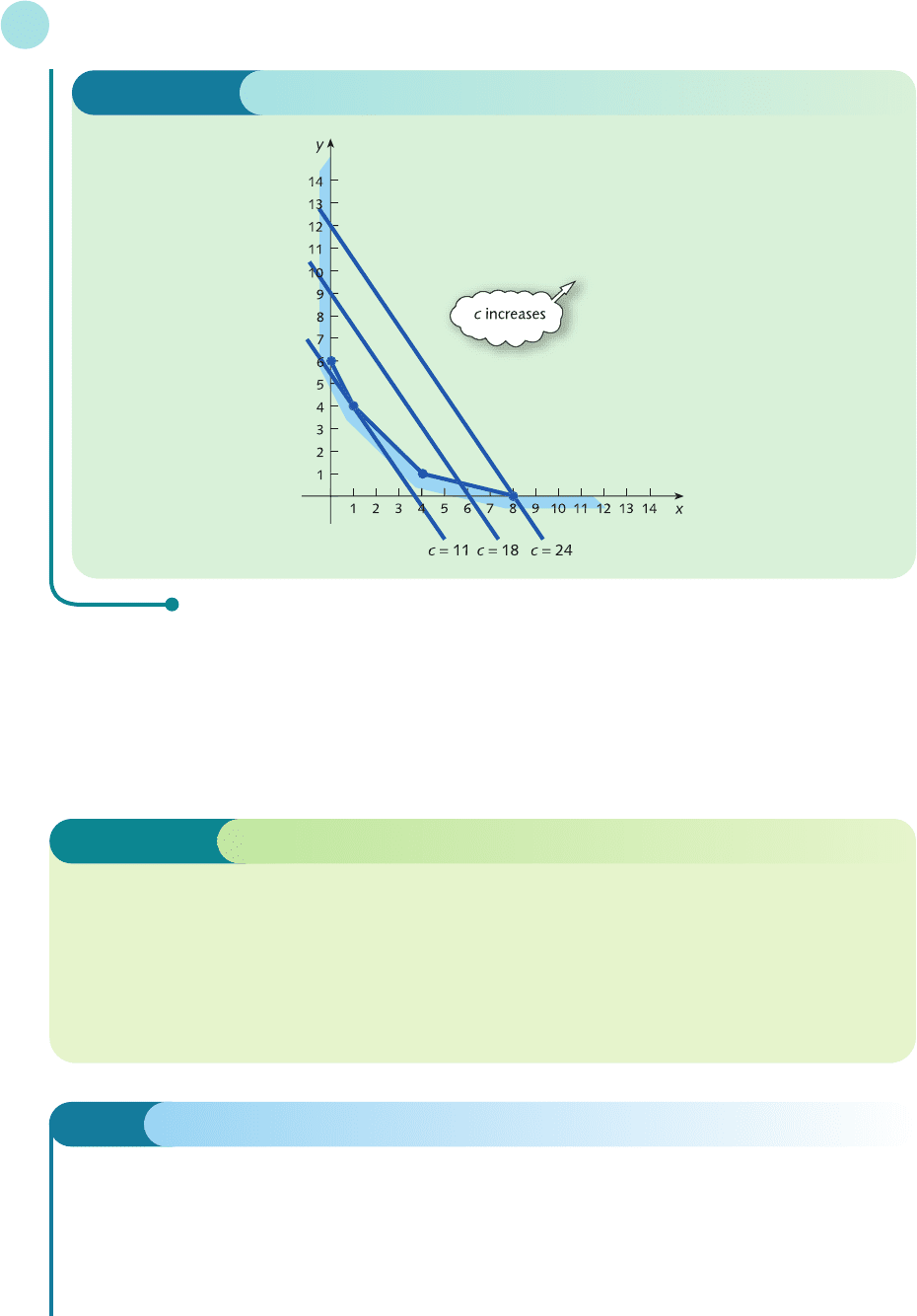
This example shows that a linear programming problem may not have a finite solution
when the feasible region is unbounded. However, when a solution does exist, it may be found
simply by inspecting the corners in the normal way. In practice, linear programming problems
arise from realistic economic situations. We would therefore expect the problem to possess a
sensible (that is, finite) answer and so the difficulty of the non-existence of a solution rarely
occurs.
Linear Programming
532
Figure 8.12
Practice Problems
6 Sketch the feasible regions defined by the following sets of inequalities:
(a)
5x + 3y ≤ 30 (b) 2x + 5y ≤ 20 (c) x − 2y ≤ 3
7x + 2y ≤ 28 x + y ≤ 5 x − y ≤ 4
x ≥ 0 x ≥ 0 x ≥ 1
y ≥ 0 y ≥ 0 y ≥ 0
Feasible region The set of points that satisfy all of the constraints in a linear programming
problem.
Non-negativity constraints The constraints, x ≥ 0, y ≥ 0, etc.
Objective function The function that is optimized in a linear programming problem.
Unbounded region A feasible region that is not completely enclosed by a polygon. The
associated linear programming problem may not have a finite solution.
Key Terms
MFE_C08a.qxd 16/12/2005 10:47 Page 532

7 Use your answers to Practice Problem 6 to solve the following linear programming problems.
(a) Maximize
4x + 9y
subject to
5x + 3y ≤ 30
7x + 2y ≤ 28
x ≥ 0
y ≥ 0
(b) Maximize 3x + 6y
subject to
2x + 5y ≤ 20
x + y ≤ 5
x ≥ 0
y ≥ 0
(c) Maximize x + y
subject to
x − 2y ≤ 3
x − y ≤ 4
x ≥ 1
y ≥ 0
8 What can you say about the solution to Practice Problem 7(c) if the problem is one of maximization
rather than minimization? Explain your answer by superimposing the family of lines
x + y = c
on the feasible region.
9 Solve the following linear programming problems.
(a) Maximize
2x + 3y (b) Maximize −8x + 4y
subject to subject to
2x + y ≤ 8 x − y ≤ 2
x + y ≤ 62x − y ≥−3
x + 2y ≤ 10 x − y ≥−4
x ≥ 0 x ≥ 0
y ≥ 0 y ≥ 0
10 Explain why each of the following problems fails to possess a solution.
(a) Maximize
x + y (b) Maximize x + y
subject to subject to
y ≥ 22x − y ≥−1
x ≤ 2 x − 2y ≤ 2
x − y ≤ 1 x ≥ 0
x ≥ 0 y ≥ 0
y ≥ 0
8.1 • Graphical solution of linear programming problems
533
MFE_C08a.qxd 16/12/2005 10:47 Page 533

11 Solve the linear programming problem
Maximize
6x + 2y
subject to
x − y ≥ 0
3x + y ≥ 8
x ≥ 0
y ≥ 0
12 Show that the linear programming problem given in Practice Problem 7(a) can be expressed in matrix
notation as
Maximize
c
T
x
subject to
Ax ≤ b
x ≥ 0
where c, x, b and 0 are 2 × 1 matrices and A is a 2 × 2 matrix, which should be stated.
Linear Programming
534
MFE_C08a.qxd 16/12/2005 10:47 Page 534

section 8.2
Applications of linear
programming
The impression possibly given so far is that linear programming is a mathematical technique
designed to solve rather abstract problems. This is misleading since linear programming
problems do arise from concrete situations. We now put the record straight by considering
three realistic examples that lead naturally to such problems. In doing so we shall develop an
important skill that can loosely be called problem formulation. Here we start with information,
perhaps only vaguely given in words, and try to express it using the more precise language
of mathematics. Once this has been done, it is a simple matter of applying mathematical
techniques to produce the solution.
Objectives
At the end of this section you should be able to:
Identify the unknowns in a linear programming problem.
Find an expression for the objective function and decide whether it should be
maximized or minimized.
Write down all of the constraints, including any obvious ones not mentioned
explicitly in the problem specification.
Solve linear programming problems expressed in words, remembering to check
that the answer makes sense.
MFE_C08b.qxd 16/12/2005 10:48 Page 535

Linear Programming
536
Example
A small manufacturer produces two kinds of good, A and B, for which demand exceeds capacity. The pro-
duction costs for A and B are $6 and $3, respectively, each, and the corresponding selling prices are $7 and $4.
In addition, the transport costs are 20 cents and 30 cents for each good of type A and B, respectively. The con-
ditions of a bank loan limit the manufacturer to maximum weekly production costs of $2700 and maximum
weekly transport costs of $120. How should the manufacturer arrange production to maximize profit?
Solution
As mentioned in Section 8.1, there are three things constituting a linear programming problem: a pair of
unknowns x and y, an objective function that needs maximizing or minimizing, and some constraints. We
consider each of these in turn.
The manufacturer has to decide exactly how many goods of types A and B to produce each week. These
are therefore the unknowns of this problem and we denote these unknowns by the letters x and y: that is,
we let
x = number of goods of type A to be made each week
y = number of goods of type B to be made each week
The final sentence of the problem states that the manufacturer should choose these quantities to maximize
profit. Hence we need to find a formula for profit in terms of x and y. Now for each good of type A the
production costs are $6 and the transport costs are 20 cents. The total cost is therefore $6.20. If the selling
price is $7, it follows that the profit made on a single item is 80 cents. Consequently, when x goods of type
A are made the total profit is x times this amount, $0.8x. Notice that the question states that ‘demand
exceeds capacity’, so all goods are guaranteed to be sold. Exactly the same reasoning can be applied to B.
The profit is 70 cents each, so when y goods of type B are made the total profit is $0.7y. Hence the profit
resulting from the production of both A and B is
0.8x + 0.7y
This then is the objective function that we want to maximize.
The next thing to do is to read through the original specification to see what restrictions are to be
imposed on the production levels. We see that the total weekly production costs must not exceed $2700. The
production costs are $6 for A and $3 for B. Hence if x goods are made of type A and y goods are made of
type B the total cost is
6x + 3y
so we require
6x + 3y ≤ 2700
Similarly, the total cost of transporting the goods is
0.2x + 0.3y
and since this must not exceed $120 we need
0.2x + 0.3y ≤ 120
On the face of it there appear to be no further constraints given in the problem. However, a moment’s
thought should convince you that we are missing two important constraints, namely
x ≥ 0 and y ≥ 0
Although these are not mentioned explicitly, it is obvious that it is impossible to manufacture a negative
number of goods.
MFE_C08b.qxd 16/12/2005 10:48 Page 536

Collecting all of the ingredients together, the linear programming problem may be stated:
Maximize 0.8x + 0.7y
subject to
6x + 3y ≤ 2700
0.2x + 0.3y ≤ 120
x ≥ 0
y ≥ 0
The problem can now be solved using the method described in Section 8.1.
Step 1
As usual the non-negativity constraints indicate that we need only consider points in the positive quadrant.
The line 6x + 3y = 2700 passes through (0, 900) and (450, 0).
The line 0.2x + 0.3y = 120 passes through (0, 400) and (600, 0).
Also, using the origin as the test point reveals that the region of interest lies below both lines. It is sketched
in Figure 8.13.
Step 2
The feasible region has four corners altogether, three of which have obvious coordinates (0, 0), (0, 400)
and (450, 0). Unfortunately it is not at all easy to read off from the diagram the exact coordinates of the
remaining corner. This is formed by the intersection of the two lines
6x + 3y = 2700 (1)
0.2x + 0.3y = 120 (2)
8.2 • Applications of linear programming
537
Figure 8.13
MFE_C08b.qxd 16/12/2005 10:48 Page 537

You may have encountered this difficulty when solving Practice Problem 8 in Section 8.1. If desired, we can
always find the exact coordinates by treating the corresponding equations as a pair of simultaneous equa-
tions and solving them algebraically. The variable x can be eliminated by multiplying equation (2) by 30 and
subtracting from (1) to get
6x + 3y = 2700
6x + 9y = 3600
−6y =−900 (3)
Equation (3) gives y = 150 and if this value is substituted into either of the original equations, it is easy to
see that x = 375. The fourth corner therefore has coordinates (375, 150).
Step 3
Linear Programming
538
Corner Objective function
(0, 0) 0
(0, 400) 280
(450, 0) 360
(375, 150) 405
The maximum weekly profit is $405, which occurs when 375 goods of type A and 150 goods of type B are
manufactured.
Advice
It is impossible to give a precise description of problem formulation. Each case has to be
considered on its own merits. However, the previous example does suggest the following
general strategy, which might be helpful:
(1) Identify the unknowns and label them x and y.
(2) Write down an expression for the objective function in terms of x and y, and decide
whether it needs maximizing or minimizing.
(3) Write down all constraints on the variables x and y.
Practice Problem
1 An electronics firm decides to launch two new models of computer, COM1 and COM2. The cost of
producing each machine of type COM1 is $1200 and the cost for COM2 is $1600. The firm recog-
nizes that it is a risky venture and decides to limit the total weekly production costs to $40 000. Also,
due to a shortage of skilled labour, the total number of computers that the firm can produce in a week
is at most 30. The profit made on each machine is $600 for COM1 and $700 for COM2. How should
the firm arrange production to maximize profit?
MFE_C08b.qxd 16/12/2005 10:48 Page 538

8.2 • Applications of linear programming
539
Example
A food producer uses two processing plants, P1 and P2 that operates 7 days a week. After processing, beef
is graded into high-, medium- and low-quality foodstuffs. High-quality beef is sold to butchers, medium-
quality beef is used in super-market ready-meals and the low-quality beef is used in dog food. The producer
has contracted to provide 120 kg of high-, 80 kg of medium- and 240 kg of low-quality beef each week. It
costs $4000 per day to run plant P1 and $3200 per day to run plant P2. Each day P1 processes 60 kg of high-
quality beef, 20 kg of medium-quality beef and 40 kg of low-quality beef. The corresponding quantities for
P2 are 20 kg, 20 kg and 120 kg, respectively. How many days each week should the plants be operated to
fulfil the beef contract most economically?
Solution
The clue to the unknowns of this problem can be found in the final sentence ‘How many days each week
. . .’. We let
x = number of days each week that plant P1 is operated
y = number of days each week that plant P2 is operated
The objective function is harder to ascertain. The phrase ‘to fulfil the contract most economically’ is rather
vague. It could mean that we want to maximize profit, as in the previous example. Unfortunately,
insufficient information is given in the problem to determine profit, since we do not know the selling prices
of the three grades of meat. We are, however, given the operating cost, so we take this to be the objective
function, which then needs to be minimized. The daily costs for plants P1 and P2 are $4000 and $3200,
respectively. Consequently, if plant P1 is operated for x days and plant P2 for y days then the total weekly
cost is
4000x + 3200y
The remaining information is used to determine the constraints. The producer has contracted to provide
120 kg of high-quality beef each week. This means that at least this amount must be processed to fulfil
MFE_C08b.qxd 16/12/2005 10:48 Page 539
