Jacques I. Mathematics for Economics and Business
Подождите немного. Документ загружается.


Matrices
500
Practice Problems
4 Use Cramer’s rule to solve
(a)
=
for x
1
(b) =
for x
2
(c) =
for x
4
5 Consider the macroeconomic model defined by
Y = C + I* + G* + X* − M
C = aY + b (0 < a < 1, b > 0)
M = mY + M* (0 < m < 1, M* > 0)
Show that this system can be written as Ax = b, where
A = x = b =
Use Cramer’s rule to show that
Y =
Write down the autonomous investment multiplier for Y and deduce that Y increases as as I* increases.
6 Consider the macroeconomic model defined by
national income: Y = C + I + G*(G* > 0)
consumption: C = aY + b (0 < a < 1, b > 0)
investment: I = cr + d (c < 0, d > 0)
money supply: M*
S
= k
1
Y + k
2
r (k
1
> 0, k
2
< 0, M*
S
> 0)
Show that this system can be written as Ax = b, where
A = x = b =
J
K
K
K
K
L
G*
b
d
M*
S
G
H
H
H
H
I
J
K
K
K
K
L
Y
C
I
r
G
H
H
H
H
I
J
K
K
K
K
L
1 −1 −10
−a 10 0
001−c
k
1
00 k
2
G
H
H
H
H
I
b + I* + G* + X* − M*
1 − a + m
J
K
K
L
I* + G* + X*
b
M*
G
H
H
I
J
K
K
L
Y
C
M
G
H
H
I
J
K
K
L
1 −11
−a 10
−m 01
G
H
H
I
J
K
K
K
K
L
−1
1
−24
15
G
H
H
H
H
I
J
K
K
K
K
L
x
1
x
2
x
3
x
4
G
H
H
H
H
I
J
K
K
K
K
L
10 23
−15 41
07−36
24 51
G
H
H
H
H
I
J
K
K
L
−15
17
−1
G
H
H
I
J
K
K
L
x
1
x
2
x
3
G
H
H
I
J
K
K
L
32−2
433
2 −11
G
H
H
I
J
K
L
13
7
G
H
I
J
K
L
x
1
x
2
G
H
I
J
K
L
4 −1
−25
G
H
I
MFE_C07c.qxd 16/12/2005 10:46 Page 500

Use Cramer’s rule to show that
r =
Write down the government expenditure multiplier for r and deduce that the interest rate, r, increases
as government expenditure, G*, increases.
7 The equations defining a model of two trading nations are given by
Y
1
= C
1
+ I*
1
+ X
1
− M
1
Y
2
= C
2
+ I*
2
+ X
2
− M
2
C
1
= 0.6Y
1
+ 50 C
2
= 0.8Y
2
+ 80
M
1
= 0.2Y
1
M
2
= 0.1Y
2
If I*
2
= 70, find the value of I*
1
if the balance of payments is zero.
[Hint: construct a system of three equations for the three unknowns, Y
1
, Y
2
and I*
1
.]
8 The equations defining a general model of two trading countries are given by
Y
1
= C
1
+ I*
1
+ X
1
− M
1
Y
2
= C
2
+ I*
2
+ X
2
− M
2
C
1
= a
1
Y
1
+ b
1
C
2
= a
2
Y
2
+ b
2
M
1
= m
1
Y
1
M
2
= m
2
Y
2
where 0 < a
i
< 1, b
i
> 0 and 0 < m
i
< 1 (i = 1, 2). Express this system in matrix form and use Cramer’s
rule to solve this system for Y
1
. Write down the multiplier for Y
1
due to changes in I*
2
and hence give
a general description of the effect on the national income of one country due to a change in invest-
ment in the other.
M*
S
(1 − a) − k
1
(b + d + G*)
k
2
(1 − a) + ck
1
7.3 • Cramer’s rule
501
MFE_C07c.qxd 16/12/2005 10:46 Page 501

section 7.4
Input–output analysis
The simplest model of the macroeconomy assumes that there are only two sectors: households
and firms. The flow of money between these sectors is illustrated in Figure 7.1.
The ‘black box’ labelled ‘firms’ belies a considerable amount of economic activity. Firms
exchange goods and services between themselves as well as providing them for external con-
sumption by households. For example, the steel industry uses raw materials such as iron ore
and coal to produce steel. This, in turn, is bought by mechanical engineering firms to produce
machine tools. These tools are then used by other firms, including those in the steel industry.
It is even possible for some businesses to use as input some of their own output. For example,
in the agricultural sector, a farm might use arable land to produce grain, some of which is
Objectives
At the end of this section you should be able to:
Understand what is meant by a matrix of technical coefficients.
Calculate the final demand vector given the total output vector.
Calculate the total output vector given the final demand vector.
Calculate the multipliers in simple input–output models.
Figure 7.1
MFE_C07d.qxd 16/12/2005 10:46 Page 502

7.4 • Input–output analysis
503
recycled as animal foodstuffs. Output destined for households is called final (or external)
demand. Output that is used as input by another (or the same) firm is called intermediate out-
put. The problem of identifying individual firms and goods, and of tracking down the flow of
money between firms for these goods, is known as input–output analysis.
Suppose that there are just two industries, I1 and I2, and that $1 worth of output of I1
requires as input 10 cents worth of I1 and 30 cents worth of I2. The corresponding figures for
I2 are 50 cents and 20 cents respectively. This information can be displayed in tabular form as
shown in Table 7.3.
The matrix obtained by stripping away the headings in Table 7.3 is
A =
and is called the matrix of technical coefficients (sometimes called the technology matrix). The
columns of A give the inputs needed to produce $1 worth of output. In general, if there are n
industries then the matrix of technical coefficients has order n × n. Element a
ij
gives the input
needed from the ith industry to produces $1 worth of output for the jth industry.
We shall make the important assumption that the production functions for each industry in
the model exhibit constant returns to scale. This means that the technical coefficients can be
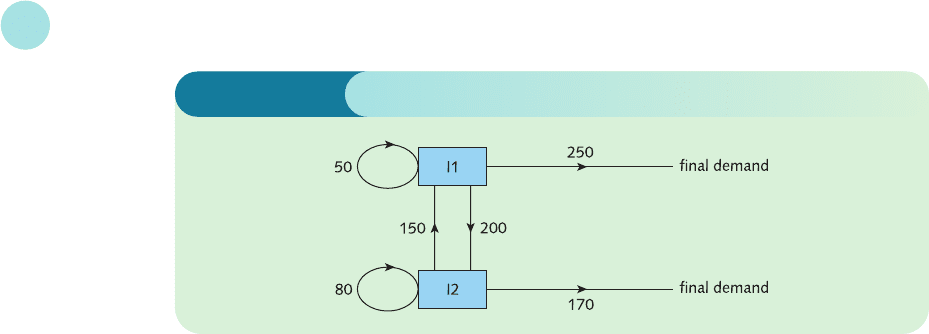
thought of as proportions that are independent of the level of output. For example, suppose
that we wish to produce 500 monetary units of output of I1 instead of just 1 unit. The first
column of A shows that the input requirements are
0.1 × 500 = 50 units of I1
0.3 × 500 = 150 units of I2
Similarly, if we produce 400 units of I2 then the second column of A shows that we use
0.5 × 400 = 200 units of I1
0.2 × 400 = 80 units of I2
In this situation, of the 500 units of I1 that are produced, 50 go back into I1 and 200 are used
in I2. This means that there are 250 units left which are available for external demand.
Similarly, of the 400 units of I2 that are produced, 230 are used as intermediate output, leaving
170 units to satisfy external demand. The flow of money for this simple input–output model is
illustrated in Figure 7.2.
For the general case of n industries we would like to be able to use the matrix of technical
coefficients to provide answers to the following questions.
Question 1
How much output is available for final demand given the total output level?
J
K
L
0.1 0.5
0.3 0.2
G
H
I
Table 7.3
Output
I1 I2
Input I1 0.1 0.5
I2 0.3 0.2
MFE_C07d.qxd 16/12/2005 10:46 Page 503
Matrices
504
Question 2
How much total output is required to satisfy a given level of final demand?
Question 3
What changes need to be made to total output when final demand changes by a given amount?
It turns out that all three questions can be answered using one basic matrix equation, which
we now derive. We begin by returning to the simple two-industry model with matrix of tech-
nical coefficients
A =
Let us denote the final demand for I1 and I2 by d
1
and d
2
respectively, and denote the total out-
puts by x
1
and x
2
. Total output from I1 gets used up in three different ways. Firstly, some of the
output from I1 gets used up as input to I1. The precise proportion is given by the element
a
11
= 0.1
so I1 uses 0.1x
1
units of its own output. Secondly, some of the output from I1 gets used as input
to I2. The element
a
12
= 0.5
gives the amount of I1 that is used to make 1 unit of I2. We make a total of x
2
units of I2, so we
use up 0.5x
2
units of I1 in this way. Finally, some of the output of I1 satisfies final demand,
which we denote by d
1
. The total amount of I1 that is used is therefore
0.1x
1
+ 0.5x
2
+ d
1
If we assume that the total output from I1 is just sufficient to meet these requirements then
x
1
= 0.1x
1
+ 0.5x
2
+ d
1
Similarly, if I2 produces output to satisfy the input requirements of the two industries as well
as final demand then
x
2
= 0.3x
1
+ 0.2x
2
+ d
2
In matrix notation these two equations can be written as
=+
J
K
L
d
1
d
2
G
H
I
J
K
L
x
1
x
2
G
H
I
J
K
L
0.1 0.5
0.3 0.2
G
H
I
J
K
L
x
1
x
2
G
H
I
J
K
L
0.1 0.5
0.3 0.2
G
H
I
Figure 7.2
MFE_C07d.qxd 16/12/2005 10:46 Page 504

7.4 • Input–output analysis
505
that is, x = Ax + d
where x is the total output vector
and d is the final demand vector
For the general case of n industries, we write x
i
and d
i
for the total output and final demand for
the ith industry. Of the x
i
units of output of industry i that are produced,
a
i1
x
1
is used as input for industry 1
a
i2
x
1
is used as input for industry 2
.
.
.
a
in
x
n
is used as input for industry n
and
d
i
is used for external demand
Hence
x
i
= a
i1
x
1
+ a
i2
x
2
+ ... + a
in
x
n
+ d
i
In matrix form, the totality of equations obtained by setting i = 1, 2,..., n, in turn, can be
written as
==
that is, as
x = Ax + d
where A is the n × n matrix of technical coefficients, x is the n × 1 total output vector and d is
the n × 1 final demand vector.
The three questions posed can now be answered.
Question 1
How much output is available for final demand given the total output level?
Answer 1
In this case the vector x is assumed to be known and we need to calculate the unknown vector
d. The matrix equation
x = Ax + d
immediately gives d = x − Ax
and the right-hand side is easily evaluated to get d.
J
K
K
K
K
L
d
1
d
2
.
.
.
d
n
G
H
H
H
H
I
J
K
K
K
K
L
x
1
x
2
.
.
.
x
n
G
H
H
H
H
I
J
K
K
K
K
L
a
11
a
12
. . . a
1n
a
21
a
22
. . . a
2n
.. . .
.. . .
.. . .
a
n1
a
n2
. . . a
nn
G
H
H
H
H
I
J
K
K
K
K
L
x
1
x
2
.
.
.
x
n
G
H
H
H
H
I
J
K
L
d
1
d
2
G
H
I
J
K
L
x
1
x
2
G
H
I
MFE_C07d.qxd 16/12/2005 10:46 Page 505

Matrices
506
Example
The output levels of machinery, electricity and oil of a small country are 3000, 5000 and 2000 respectively.
Each unit of machinery requires inputs of 0.3 units of electricity and 0.3 units of oil.
Each unit of electricity requires inputs of 0.1 units of machinery and 0.2 units of oil.
Each unit of oil requires inputs of 0.2 units of machinery and 0.1 units of electricity.
Determine the machinery, electricity and oil available for export.
Solution
Let us denote the total output for machinery, electricity and oil by x
1
, x
2
and x
3
respectively, so that
x
1
= 3000, x
2
= 5000, x
3
= 2000
The first bullet point of the problem statement provides details of the input requirements for machinery. To
produce 1 unit of machinery we use 0 units of machinery, 0.3 units of electricity and 0.3 units of oil. The
first column of the matrix of technical coefficients is therefore
Likewise, the third and fourth sentences give the input requirements for electricity and oil, so the complete
matrix is
A =
From the equation
d = x − Ax
we see that the final demand vector is
=−
=−
=
The country therefore has 2100, 3900 and 100 units
of machinery, electricity and oil, respectively,
available for export.
J
K
K
L
2100
3900
100
G
H
H
I
J
K
K
L
900
1100
1900
G
H
H
I
J
K
K
L
3000
5000
2000
G
H
H
I
J
K
K
L
3000
5000
2000
G
H
H
I
J
K
K
L
0 0.1 0.2
0.3 0 0.1
0.3 0.2 0
G
H
H
I
J
K
K
L
3000
5000
2000
G
H
H
I
J
K
K
L
d
1
d
2
d
3
G
H
H
I
J
K
K
L
0 0.1 0.2
0.3 0 0.1
0.3 0.2 0
G
H
H
I
J
K
K
L
0
0.3
0.3
G
H
H
I
MFE_C07d.qxd 16/12/2005 10:46 Page 506

Question 2
How much total output is required to satisfy a given level of final demand?
Answer 2
In this case the vector d is assumed to be known and we need to calculate the unknown vector
x. The matrix equation
x = Ax + d
rearranges to give
x − Ax = d
or equivalently
(I − A)x = d
because
(I − A)x = Ix − Ax = x − Ax
This represents a system of linear equations in which the coefficient matrix is I − A and the
right-hand-side vector is d. From Section 7.2 we know that we can solve this by multiplying the
inverse of the coefficient matrix by the right-hand-side vector to get
x = (I − A)
−1
d
In the context of input–output analysis the matrix (I − A)
−1
is called the Leontief inverse.
7.4 • Input–output analysis
507
Practice Problem
1 Determine the final demand vector for three firms given the matrix of technical coefficients
A =
and the total output vector
x =
J
K
K
L
1000
300
700
G
H
H
I
J
K
K
L
0.2 0.4 0.2
0.1 0.2 0.1
0.1 0.1 0
G
H
H
I
Example
Given the matrix of technical coefficients
A =
for three industries, I1, I2 and I3, determine the total outputs required to satisfy final demands of 49, 106
and 17 respectively.
J
K
K
L
0.3 0.1 0.1
0.2 0.2 0.2
0.4 0.2 0.3
G
H
H
I
MFE_C07d.qxd 16/12/2005 10:46 Page 507

Solution
To solve this problem we need to find the inverse of I − A and then to multiply by the final demand vector.
The matrix I − A is
−=
The inverse of this matrix is then found by calculating its cofactors. If we call this matrix B then the co-
factors, B
ij
, corresponding to elements b
ij
are given by
B
11
= 0.52, B
12
= 0.22, B
13
= 0.36
B
21
= 0.09, B
22
= 0.45, B
23
= 0.18
B
31
= 0.10, B
32
= 0.16, B
33
= 0.54
By expanding along the first row we see that
|B|=0.7(0.52) + (−0.1)(0.22) + (−0.1)(0.36) = 0.306
Hence
B
−1
= ( I − A)
−1
=
We are given that
d =
so the equation
x = (I − A)
−1
d
gives
==
J
K
K
L
120
200
150
G
H
H
I
J
K
K
L
49
106
17
G
H
H
I
J
K
K
L
0.52 0.09 0.10
0.22 0.45 0.16
0.36 0.18 0.54
G
H
H
I
1
0.306
J
K
K
L
x
1
x
2
x
3
G
H
H
I
J
K
K
L
49
106
17
G
H
H
I
J
K
K
L
0.52 0.09 0.10
0.22 0.45 0.16
0.36 0.18 0.54
G
H
H
I
1
0.306
J
K
K
L
0.7 −0.1 −0.1
−0.2 0.8 −0.2
−0.4 −0.2 0.7
G
H
H
I
J
K
K
L
0.3 0.1 0.1
0.2 0.2 0.2
0.4 0.2 0.3
G
H
H
I
J
K
K
L
100
010
001
G
H
H
I
Matrices
508
Practice Problem
2 Each unit of engineering output requires as input 0.2 units of engineering and 0.4 units of transport.
Each unit of transport output requires as input 0.2 units of engineering and 0.1 units of transport.
Determine the level of total output needed to satisfy a final demand of 760 units of engineering and
420 units of transport.
Question 3
What changes need to be made to total output when final demand changes by a given amount?
MFE_C07d.qxd 16/12/2005 10:46 Page 508

Answer 3
In this case we assume that the current total output vector, x, is chosen to satisfy some existing
final demand vector, d, so that
x = Ax + d
or equivalently
x = (I − A)
−1
d (1)
Suppose that the final demand vector changes by an amount ∆d, so that the new final demand
vector is d +∆d. In order to satisfy the new requirements, the total output vector, x +∆x, is
then given by
x +∆x = (I − A)
−1
(d +∆d)
= (I − A)
−1
d + (I − A)
−1
∆d (2)
where we have used the distributive law to multiply out the brackets. However, from equation
(1) we know that
(I − A)
−1
d = x
so equation (2) becomes
x +∆x = x + (I − A)
−1
∆d
and if x is subtracted from both sides then
∆x = (I − A)
−1
∆d
Notice that this equation does not have d or x in it. This shows that the change in output, ∆x,
does not depend on the existing final demand or existing total output. It depends only on the
change, ∆d. It is also interesting to observe that the mathematics needed to solve this is the
same as that for Question 2. Both require the calculation of the Leontief inverse followed by a
simple matrix multiplication.
7.4 • Input–output analysis
509
Example
Consider the following inter-industrial flow table for two industries, I1 and I2.
Assuming that the total output is just sufficient to meet the input and final demand requirements, write
down
(a) the total output vector
(b) the matrix of technical coefficients
Hence calculate the new total output vector needed when the final demand for I1 rises by 100 units.
Output
I1 I2 Final demand
Input I1 200 300 500
I2 100 100 300
MFE_C07d.qxd 16/12/2005 10:46 Page 509
