Jacques I. Mathematics for Economics and Business
Подождите немного. Документ загружается.


Solution
(a) To calculate the current total outputs for I1 and I2 all we have to do is to add together the numbers
along each row of the table. The first row shows that I1 uses 200 units of I1 as input, I2 uses 300 units
of I1 as input and 500 units of I1 are used in final demand. The total number of units of I1 is then
200 + 300 + 500 = 1000
Assuming that the total output of I1 exactly matches these requirements, we can deduce that
x
1
= 1000
Similarly, from the second row of the table,
x
2
= 100 + 100 + 300 = 500
Hence the total output vector is
x =
(b) The first column of the matrix of technical coefficients represents the inputs needed to produce 1 unit
of I1. The first column of the inter-industrial flow table gives the inputs needed to produce the current
total output of I1, which we found in part (a) to be 1000. In all input–output models we assume that
production is subject to constant returns to scale, so we divide the first column of the inter-industrial
flow table by 1000 to find the inputs needed to produce just 1 unit of output. In part (a) the total out-
put for I2 was found to be 500, so the second column of the matrix of technical coefficients is calculated
by dividing the second column of the inter-industrial flow table by 500. Hence
A =
=
If the demand for I1 rises by 100 units and the demand for I2 remains constant, the vector giving the
change in final demand is
∆d =
To determine the corresponding change in output we use the equation
∆x = (I − A)
−1
∆d
Subtracting A from the identity matrix gives
I − A =− =
which has determinant
|I − A |=(0.8)(0.8) − (−0.6)(−0.1) = 0.58
The inverse of I − A is then
(I − A)
−1
=
J
K
L
0.8 0.6
0.1 0.8
G
H
I
1
0.58
J
K
L
0.8 −0.6
−0.1 0.8
G
H
I
J
K
L
0.2 0.6
0.1 0.2
G
H
I
J
K
L
10
01
G
H
I
J
K
L
100
0
G
H
I
J
K
L
0.2 0.6
0.1 0.2
G
H
I
J
K
K
K
K
L
200 300
1000 500
100 100
1000 500
G
H
H
H
H
I
J
K
L
1000
500
G
H
I
Matrices
510
MFE_C07d.qxd 16/12/2005 10:46 Page 510

so
∆x ==
to the nearest unit. There is an increase in total output of I2 despite the fact that the final demand for
I2 remains unchanged. This is to be expected because in order to meet the increase in final demand for
I1 it is necessary to raise output of I1, which in turn requires more inputs of both I1 and I2. Any change
to just one industry has a knock-on effect throughout all of the industries in the model.
From part (a) the current total output vector is
x =
so the new total output vector is
x +∆x =+=
J
K
L
1138
517
G
H
I
J
K
L
138
17
G
H
I
J
K
L
1000
500
G
H
I
J
K
L
1000
500
G
H
I
J
K
L
138
17
G
H
I
J
K
L
100
0
G
H
I
J
K
L
0.8 0.6
0.1 0.8
G
H
I
1
0.58
7.4 • Input–output analysis
511
Practice Problems
3 Write down the 4 × 4 matrix of technical coefficients using the information provided in the following
inter-industrial flow table. You may assume that the total outputs are just sufficient to satisfy the input
requirements and final demands.
4 Given the matrix of technical coefficients
I1 I2 I3
A =
determine the changes in total output for the three industries when the final demand for I1 rises by
1000 units and the final demand for I3 falls by 800 units simultaneously.
J
K
K
L
0.1 0.2 0.2
0.1 0.1 0.1
0.1 0.3 0.1
G
H
H
I
I1
I2
I3
Output
I1 I2 I3 I4 Final demand
Input I1 0 300 100 100 500
I2 100 0 200 100 100
I3 200 100 0 400 1300
I4 300 0 100 0 600
We conclude this section with a postscript highlighting again the connection between the
multiplier concept and the matrix inverse. Suppose that we have a three-industry model and
that the Leontief inverse, (I − A)
−1
, is given by
MFE_C07d.qxd 16/12/2005 10:46 Page 511

The equation
x = (I − A)
−1
d
is then
=
so that
x
1
= b
11
d
1
+ b
12
d
2
+ b
13
d
3
x
2
= b
21
d
1
+ b
22
d
2
+ b
23
d
3
x
3
= b
31
d
1
+ b
32
d
2
+ b
33
d
3
The first equation shows that x
1
is a function of the three variables d
1
, d
2
and d
3
. Consequently,
we can write down three partial derivatives
= b
11
, = b
12
, = b
13
In the same way, the second and third equations give
= b
21
, = b
22
, = b
23
= b
31
, = b
32
, = b
33
Recall from Chapter 5 that partial derivatives determine the multipliers in economic models.
These nine partial derivatives show that if we regard the final demands as exogenous variables
and the total outputs as endogenous variables then the multipliers are the elements in the
matrix (I − A)
−1
. More precisely, the multiplier of the variable x
i
due to changes in d
j
is the
element b
ij
, which lies in the ith row and jth column of (I − A)
−1
. This result can also be seen
more directly from the equation
∆x = (I − A)
−1
∆d
If we put ∆x = [∆x
1
∆x
2
∆x
3
]
T
and ∆d = [∆d
1
∆d
2
∆d
3
]
T
then this matrix equation
leads to
∆x
1
= b
11
∆d
1
+ b
12
∆d
2
+ b
13
∆d
3
∆x
2
= b
21
∆d
1
+ b
22
∆d
2
+ b
23
∆d
3
∆x
3
= b
31
∆d
1
+ b
32
∆d
2
+ b
33
∆d
3
We see from the ith equation that the contribution to the change ∆x
i
due to the change ∆d
j
is
b
ij
∆d
j
. In other words, if d
j
changes by ∆d
j
and all other final demands are fixed, then we can
calculate the corresponding change in x
i
by multiplying ∆d
j
by b
ij
.
∂x
3
∂d
3
∂x
3
∂d
2
∂x
3
∂d
1
∂x
2
∂d
3
∂x
2
∂d
2
∂x
2
∂d
1
∂x
1
∂d
3
∂x
1
∂d
2
∂x
1
∂d
1
J
K
K
L
d
1
d
2
d
3
G
H
H
I
J
K
K
L
b
11
b
12
b
13
b
21
b
22
b
23
b
31
b
32
b
33
G
H
H
I
J
K
K
L
x
1
x
2
x
3
G
H
H
I
J
K
K
L
b
11
b
12
b
13
b
21
b
22
b
23
b
31
b
32
b
33
G
H
H
I
Matrices
512
MFE_C07d.qxd 16/12/2005 10:46 Page 512

7.4 • Input–output analysis
513
External demand Output that is used by households.
Final demand An alternative to ‘external demand’.
Input–output analysis Examination of how inputs and outputs from various sectors of
the economy are matched to the total resources available.
Intermediate output Output from one sector which is used as input by another (or the
same) sector.
Leontief inverse The inverse of I − A, where A is the matrix of technical coefficients.
Matrix of technical coefficients (or technology matrix) A square matrix in which element
a
ij
is the input required from the ith sector to produce 1 unit of output for the jth sector.
Key Terms
Practice Problems
5 Calculate the available final demand for five firms if the matrix of technical coefficients is
F1 F2 F3 F4 F5
and the total output vector is
[1000 1500 2000 5000 1000]
T
6 Each unit of water output requires inputs of 0.1 units of steel and 0.2 units of electricity.
Each unit of steel output requires inputs of 0.1 units of water and 0.2 units of electricity.
Each unit of electricity output requires inputs of 0.2 units of water and 0.1 units of steel.
(a) Determine the level of total output needed to satisfy a final demand of 750 units of water, 300
units of steel and 700 units of electricity.
(b) Write down the multiplier for water output due to changes in final demand for electricity. Hence
calculate the change in water output due to a 100 unit increase in final demand for electricity.
7 Consider the following inter-industrial flow table for two industries I1 and I2.
J
K
K
K
K
K
L
0 0.1 0.1 0 0.2
0.1 0 0.2 0 0.1
0 0 0 0.3 0.1
0.2 0.1 0.1 0 0.1
0 0.3 0 0.1 0
G
H
H
H
H
H
I
F1
F2
F3
F4
F5
Output
I1 I2 Final demand
Input I1 100 100 300
I2 200 500 300
MFE_C07d.qxd 16/12/2005 10:46 Page 513

Assuming that the total output is just sufficient to meet the input and final demand requirements, find
(a) the current total output vector, x
(b) the matrix of technical coefficients, A
(c) the matrix of multipliers, (I − A)
−1
(d) the future total output vector, x +∆x, if final demand for I1 rises by 150 units and final demand
for I2 falls by 50 units simultaneously
8 An economy consists of three industries: agriculture, mining and manufacturing.
One unit of agricultural output requires 0.2 units of its own output, 0.3 units of mining output and
0.4 units of manufacturing output.
One unit of mining output requires 0.2 units of agricultural output, 0.4 units of its own output and
0.2 units of manufacturing output.
One unit of manufacturing output requires 0.3 units of agricultural output, 0.3 units of mining output
and 0.1 units of its own output.
(a) Write down the matrix of technical coefficients and find the Leontief inverse.
(b) Determine the levels of total output needed to satisfy a final demand of 10 000 units of agricultural
output, 30 000 units of mining output and 40 000 units of manufacturing output.
(c) If the final demand for agricultural output rises by 1000 units and the final demand for manufac-
turing output falls by 1000 units, calculate the change in mining output.
Matrices
514
MFE_C07d.qxd 16/12/2005 10:46 Page 514

chapter 8
Linear Programming
Several methods were described in Chapter 5 for optimizing functions of two
variables subject to constraints. In economics not all relationships between variables
are represented by equations and we now consider the case when the constraints
are given by inequalities. Provided the function to be optimized is linear and the
inequalities are all linear, the problem is said to be one of linear programming. For
simplicity we concentrate on problems involving just two unknowns and describe a
graphical method of solution.
There are two sections, which should be read in the order that they appear. Section
8.1 describes the basic mathematical techniques and considers special cases when
problems have either no solution or infinitely many solutions. Section 8.2 shows
how an economic problem, initially given in words, can be expressed as a linear
programming problem and hence solved.
The material in this chapter can be read at any stage, since it requires only an under-
standing of how to sketch a straight line on graph paper.
MFE_C08a.qxd 16/12/2005 10:47 Page 515

MFE_C08a.qxd 16/12/2005 10:47 Page 516

section 8.1
Graphical solution of linear
programming problems
In this and the following section we show you how to set up and solve linear programming
problems. This process falls naturally into two separate phases. The first phase concerns prob-
lem formulation; a problem, initially given in words, is expressed in mathematical symbols.
The second phase involves the actual solution of such a problem. Experience indicates that stu-
dents usually find the first phase the more difficult. For this reason, we postpone consideration
of problem formulation until Section 8.2 and begin by investigating techniques for their math-
ematical solution.
Objectives
At the end of this section you should be able to:
Identify the region defined by a linear inequality.
Sketch the feasible region defined by simultaneous linear inequalities.
Solve linear programming problems graphically.
Appreciate that a linear programming problem may have infinitely many solutions.
Appreciate that a linear programming problem may have no finite solution.
Advice
You may like to glance at one or two of the examples given in Section 8.2 now to get a
feel for the type of problem that can be solved using these techniques.
Before you can consider linear programming it is essential that you know how to sketch
linear inequalities. In Section 1.1 we discovered that a linear equation of the form
dx + ey = f
MFE_C08a.qxd 16/12/2005 10:47 Page 517
can be represented by a straight line on graph paper. We can give a similar graphical interpreta-
tion for linear inequalities involving two variables when the equals sign is replaced by one of
< (less than)
≤ (less than or equal to)
> (greater than)
≥ (greater than or equal to)
To illustrate this consider the simple inequality
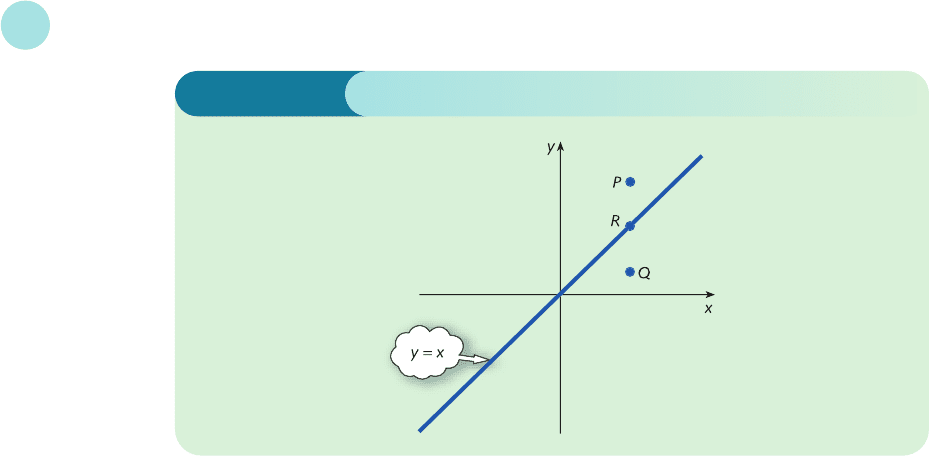
y ≥ x
We would like to identify those points with coordinates (x, y) for which this inequality is true.
Clearly this has something to do with the straight line
y = x
sketched in Figure 8.1.
If a point P lies above the line then the y coordinate is greater than the x coordinate, so that
y > x
Similarly, if a point Q lies below the line then the y coordinate is less than the x coordinate,
so that
y < x
Of course, the coordinates of a point R which actually lies on the line satisfy
y = x
Hence we see that the inequality
y ≥ x
holds for any point that lies on or above the line y = x.
It is useful to be able to indicate this region pictorially. We do this by shading one half of the
coordinate plane. There are actually two schools of thought here. Some people like to shade the
region containing the points for which the inequality is true. Others prefer to shade the region
Linear Programming
518
Figure 8.1
MFE_C08a.qxd 16/12/2005 10:47 Page 518

for which it is false. In this book we adopt the latter approach and always shade the region that
we are not interested in, as shown in Figure 8.2. This may seem a strange choice, but the
reason for making it will soon become apparent.
In general, to sketch an inequality of the form
dx + ey < f
dx + ey ≤ f
dx + ey > f
dx + ey ≥ f
we first sketch the corresponding line
dx + ey = f
and then decide which side of the line to deal with. An easy way of doing this is to pick a ‘test
point’, (x, y). It does not matter what point is chosen, provided it does not actually lie on the
line itself. The numbers x and y are then substituted into the original inequality. If the inequal-
ity is satisfied then the side containing the test point is the region of interest. If not, then we go
for the region on the other side of the line.
8.1 • Graphical solution of linear programming problems
519
Figure 8.2
Example
Sketch the region
2x + y < 4
Solution
We first sketch the line
2x + y = 4
When x = 0 we get
y = 4
MFE_C08a.qxd 16/12/2005 10:47 Page 519
