Jacques I. Mathematics for Economics and Business
Подождите немного. Документ загружается.


5 (a) 40; (b) 0.7; (C − 40); 100.
6 (a) S = 0.1Y − 72; (b) S = .
7 (a) 325; (b) 225; (c) 100.
8 C =
9 825.
10 Y = 2500, r = 10.
11 (a) C = 120 + 0.8Y;
(b) C = 40 + 0.8Y;
(c) C = 120 + 0.6Y.
With a lump sum tax, the graph has the same slope but
has been shifted downwards.
With a proportional tax, the graph has the same
intercept but is less steep.
(a) 600; (b) 200; (c) 300.
12 0.9Y + 30; 300.
(a) Slope decreases; 150. (b) Shifts up 5 units; 350.
Chapter 2
Section 2.1
1 (a) x
2
− 100 = 0
x
2
= 100
x =±√100
x =±10
(b) 2x
2
− 8 = 0
2x
2
= 8
x
2
= 4
x =±√4
x =±2
(c) x
2
− 3 = 0
x
2
= 3
x =±√3
x =±1.73 (to 2 decimal places)
(d) x
2
− 5.72 = 0
x
2
= 5.72
x =±√5.72
x =±2.39 (to 2 decimal places)
(e) x
2
+ 1 = 0
x
2
=−1
This equation does not have a solution, because
the square of a number is always positive. Try
using your calculator to find √(−1). An error
message should be displayed.
aI* + b
1 − a
10Y − 500
Y + 10
10
7
(f) 3x
2
+ 6.21 = 0
3x
2
=−6.21
x
2
=−2.07
This equation does not have a solution, because it
is impossible to find the square root of a negative
number.
(g) x
2
= 0
This equation has exactly one solution, x = 0.
2 (a) a = 2, b =−19, c =−10.
x
=
This equation has two solutions:
x ==10
x ==−
(b) a = 4, b = 12, c = 9.
x
=
This equation has one solution, x =−
3
/2.
(c) a = 1, b = 1, c = 1.
x
This equation has no solutions, because (−3)
does not exist.
(d) We first need to collect like terms to convert
x
2
− 3x + 10 = 2x + 4
into the standard form
ax
2
+ bx + c = 0
Subtracting 2x + 4 from both sides gives
x
2
− 5x + 6 = 0
a = 1, b =−5, c = 6.
=
−± −
()13
2
=
−± −
( )114
2
=
−± −
(( ) ( )( ))
()
11411
21
2
−12 ± 0
8
=
−± −
( )12 144 144
8
=
−± −
(( ) ( )( ))
()
12 12 4 4 9
24
2
1
2
19 − 21
4
19 + 21
4
19 ± 21
4
=
±
19 441
4
=
±+
( )19 361 80
4
=
−− ± − − −
( ) (( ) ( )( ))
()
19 19 4 2 10
22
2
Solutions to Problems
610
MFE_Z02.qxd 16/12/2005 10:51 Page 610
x
=
This equation has two solutions:
x ==3
x ==2
3 (a) If (x − 4) (x + 3) = 0 then either
x − 4 = 0 with solution x = 4
or
x + 3 = 0 with solution x =−3
This equation has two solutions, x = 4 and x =−3.
(b) If x(10 − 2x) = 0 then either
x = 0
or
10 − 2x = 0 with solution x = 5
This equation has two solutions, x = 0 and x = 5.
(c) If (2x − 6)(2x − 6) = 0 then
2x − 6 = 0 with solution x = 3
This equation has one solution, x = 3.
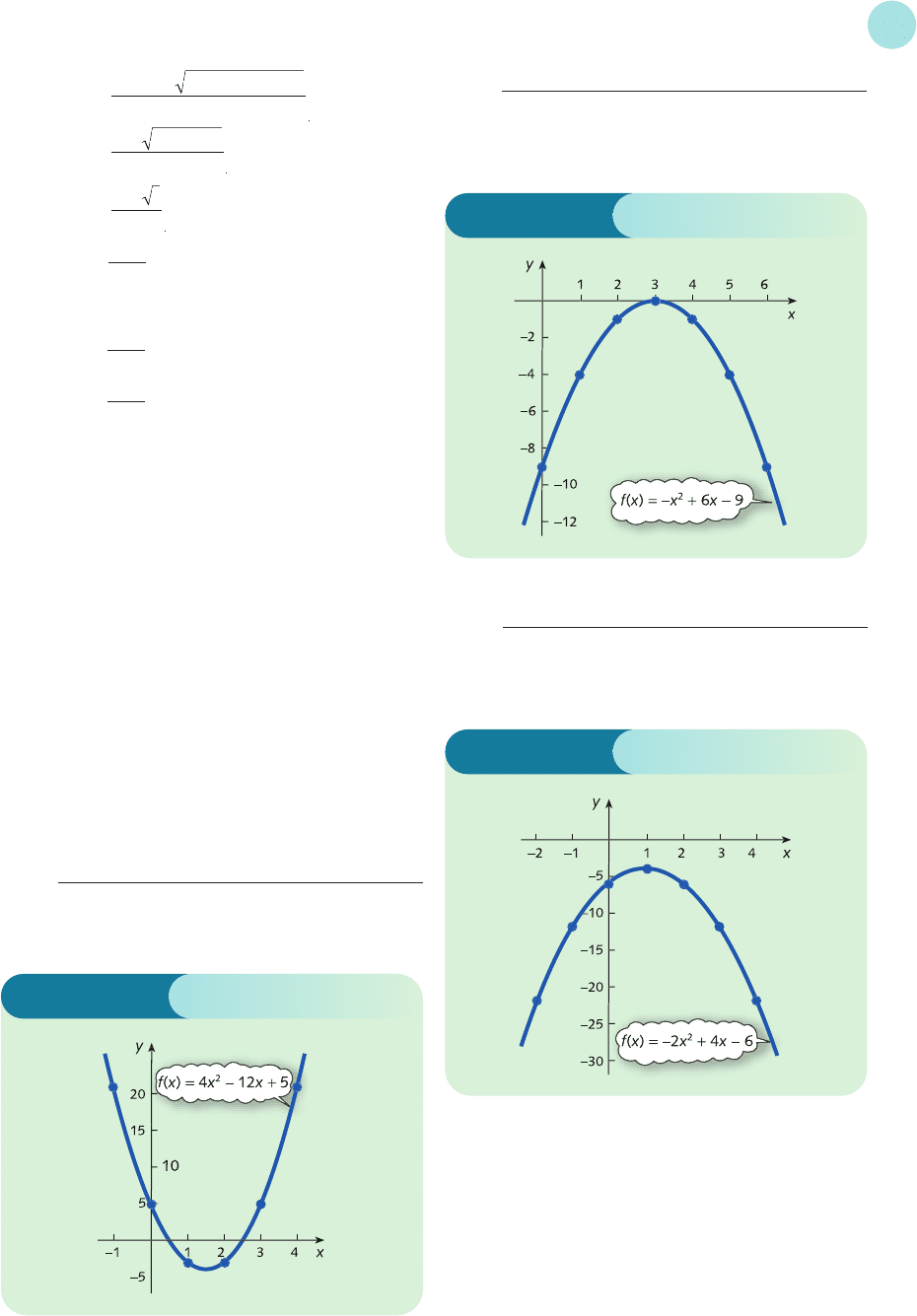
4 (a) x −10 1 23 4
f(x)215−3 −3521
The graph is sketched in Figure S2.1.
5 − 1
2
5 + 1
2
5 ± 1
2
=
±
51
2
=
±−
( )52524
2
=
−− ± − −
( ) (( ) ( )( ))
()
55416
21
2
(c) x −2 −1012 3 4
f(x) −22 −12 −6 −4 −6 −12 −22
The graph is sketched in Figure S2.3.
Solutions to Problems
611
(b) x 0123456
f(x) −9 −4 −10−1 −4 −9
The graph is sketched in Figure S2.2.
Figure S2.1
Figure S2.2
Figure S2.3
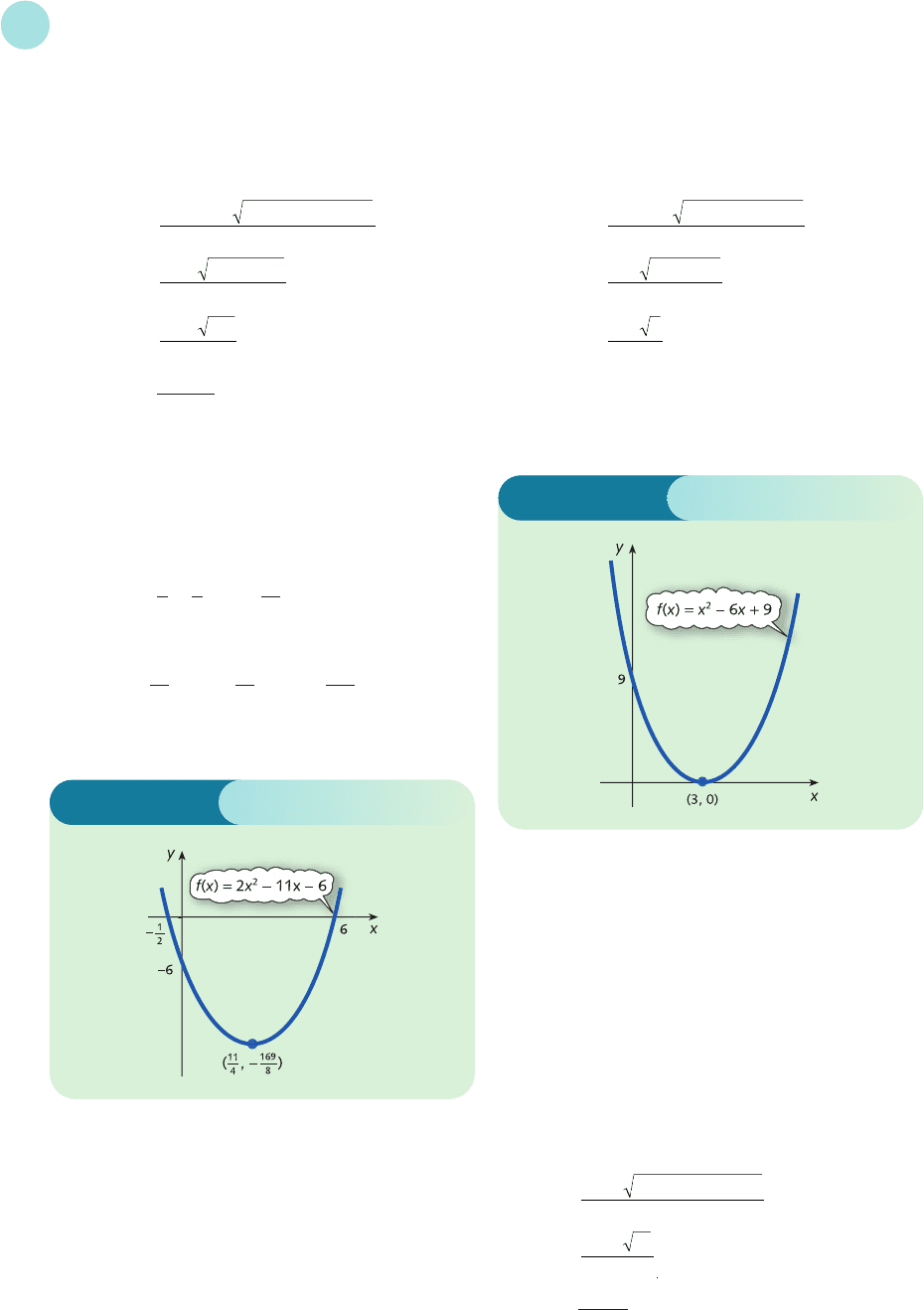
5 (a) Step 1
The coefficient of x
2
is 2, which is positive, so the
graph is U-shaped.
Step 2
The constant term is −6, so the graph crosses the
vertical axis at y =−6.
MFE_Z02.qxd 16/12/2005 10:51 Page 611
Step 3
The quadratic equation
2x
2
− 11x − 6 = 0
has solution
x
=
so the graph crosses the horizontal axis at x =−
1
/2
and x = 6.
In fact, we can use symmetry to locate the
coordinates of the turning point on the curve.
The x coordinate of the minimum occurs halfway
between x =−
1
/2 and x = 6 at
x =−+6 =
The corresponding y coordinate is
2
2
− 11 − 6 =−
The graph is sketched in Figure S2.4.
169
8
D
F
11
4
A
C
D
F
11
4
A
C
11
4
D
F
1
2
A
C
1
2
11 ± 13
4
=
±
11 169
4
=
±+
( )11 121 48
4
=
−− ± − −
( ) (( ) ( )( ))
()
11 11 4 2 6
22
2
Step 3
The quadratic equation
x
2
− 6x + 9 = 0
has solution
x
so the graph crosses the x axis at x = 3.
The graph is sketched in Figure S2.5.
=
±
=
60
2
3
=
±−
( )63636
2
=
−− ± − −
( ) (( ) ( )( ))
()
66419
21
2
Solutions to Problems
612
6 In equilibrium, Q
S
= Q
D
= Q, so the supply and
demand equations become
P = 2Q
2
+ 10Q + 10
P =−Q
2
− 5Q + 52
Hence
2Q
2
+ 10Q + 10 =−Q
2
− 5Q + 52
3Q
2
+ 15Q − 42 = 0
(collecting like terms)
Q
2
+ 5Q − 14 = 0
(dividing both sides by 3)
Q
=
−5 ± 9
2
=
−±
581
2
=
−± − −
(( ) ( )( ))
()
554114
21
2
(b) Step 1
The coefficient of x is 1, which is positive, so the
graph is U-shaped.
Step 2
The constant term is 9, so the graph crosses the
vertical axis at y = 9.
Figure S2.4
Figure S2.5
MFE_Z02.qxd 16/12/2005 10:51 Page 612
so Q =−7 and Q = 2. Ignoring the negative solution
gives Q = 2. From the supply equation, the
corresponding equilibrium price is
P = 2(2)
2
+ 10(2) + 10 = 38
As a check, the demand equation gives
P =−(2)
2
− 5(2) + 52 = 38
7 (a) ±9; (b) ±6; (c) ±2;
(d) −2, 4; (e) −9, −1; (f) −2, 9.
8 (a) 1, −3; (b)
1
/2
, −10; (c) 0, −5;
(d) −
5
/3,
9
/4; (e)
5
/4, 5; (f) 2, −1, 4.
9 (a) 0.44, 4.56; (b) −2.28, 0.22; (c) −0.26, 2.59;
(d) −0.30, 3.30; (e) −2; (f ) no solutions.
10 (a) −4, 4; (b) 0, 100; (c) 5, 17;
(d) 9; (e) no solution.
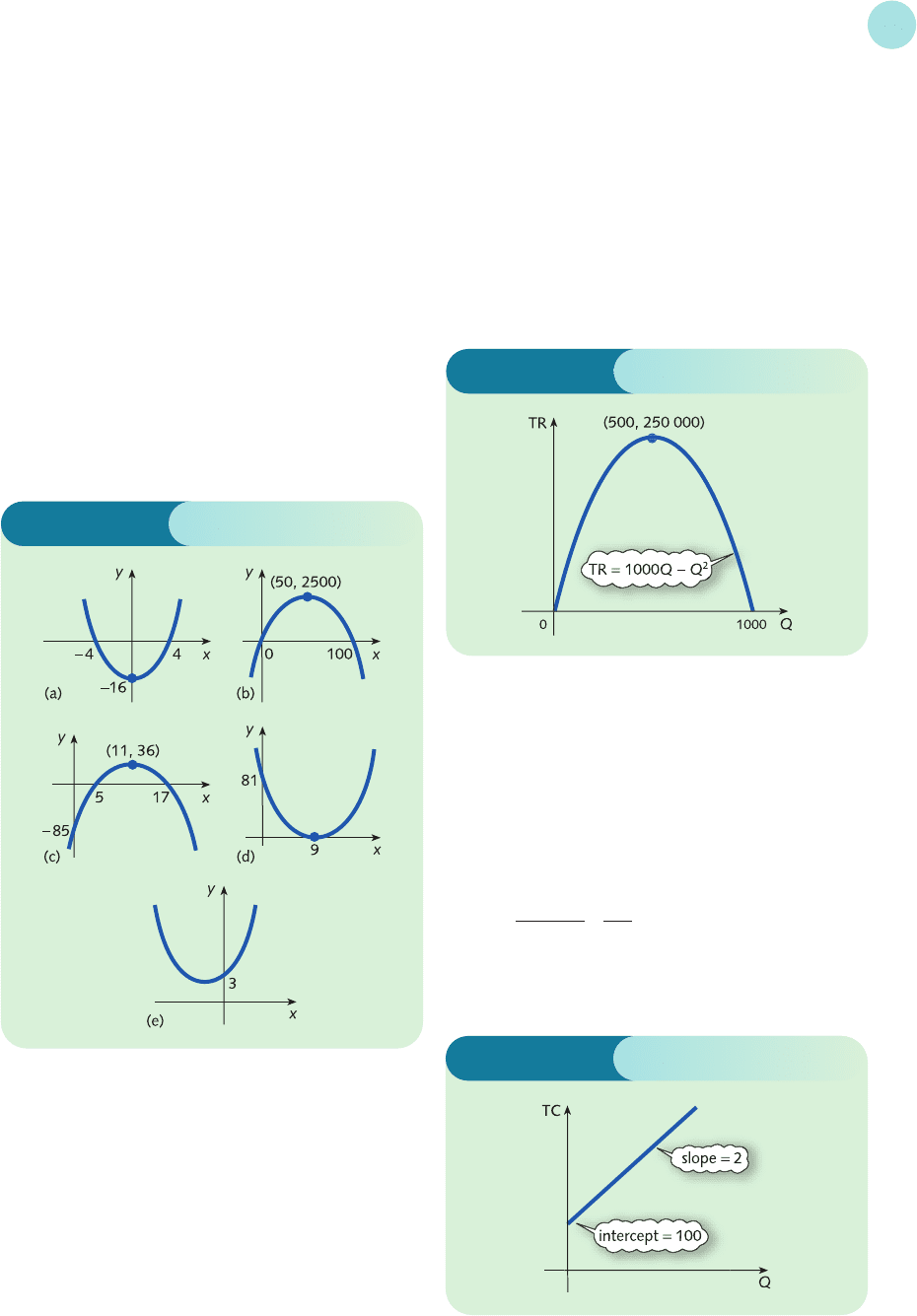
11 The graphs are sketched in Figure S2.6.
Step 2
The constant term is zero, so the graph crosses the
vertical axis at the origin.
Step 3
From the factorization
TR = (1000 − Q)Q
the graph crosses the horizontal axis at Q = 0 and
Q = 1000.
Solutions to Problems
613
The graph is sketched in Figure S2.7. By symmetry the
parabola reaches its maximum halfway between 0 and
1000 at Q = 500. The corresponding value of TR is
TR = 1000(500) − (500)
2
= 250 000
From the demand equation, when Q = 500,
P = 1000 − 500 = 500
2 TC = 100 + 2Q
AC ==+2
The graph of the total cost function is sketched in
Figure S2.8.
100
Q
100 + 2Q
Q
12 c = 12; 6.
13 Q = 4, P = 36.
14 P = 22, Q = 3.
Section 2.2
1 TR = PQ = (1000 − Q)Q = 1000Q − Q
2
Step 1
The coefficient of Q
2
is negative, so the graph has an
inverted U shape.
Figure S2.6
Figure S2.7
Figure S2.8
MFE_Z02.qxd 16/12/2005 10:51 Page 613
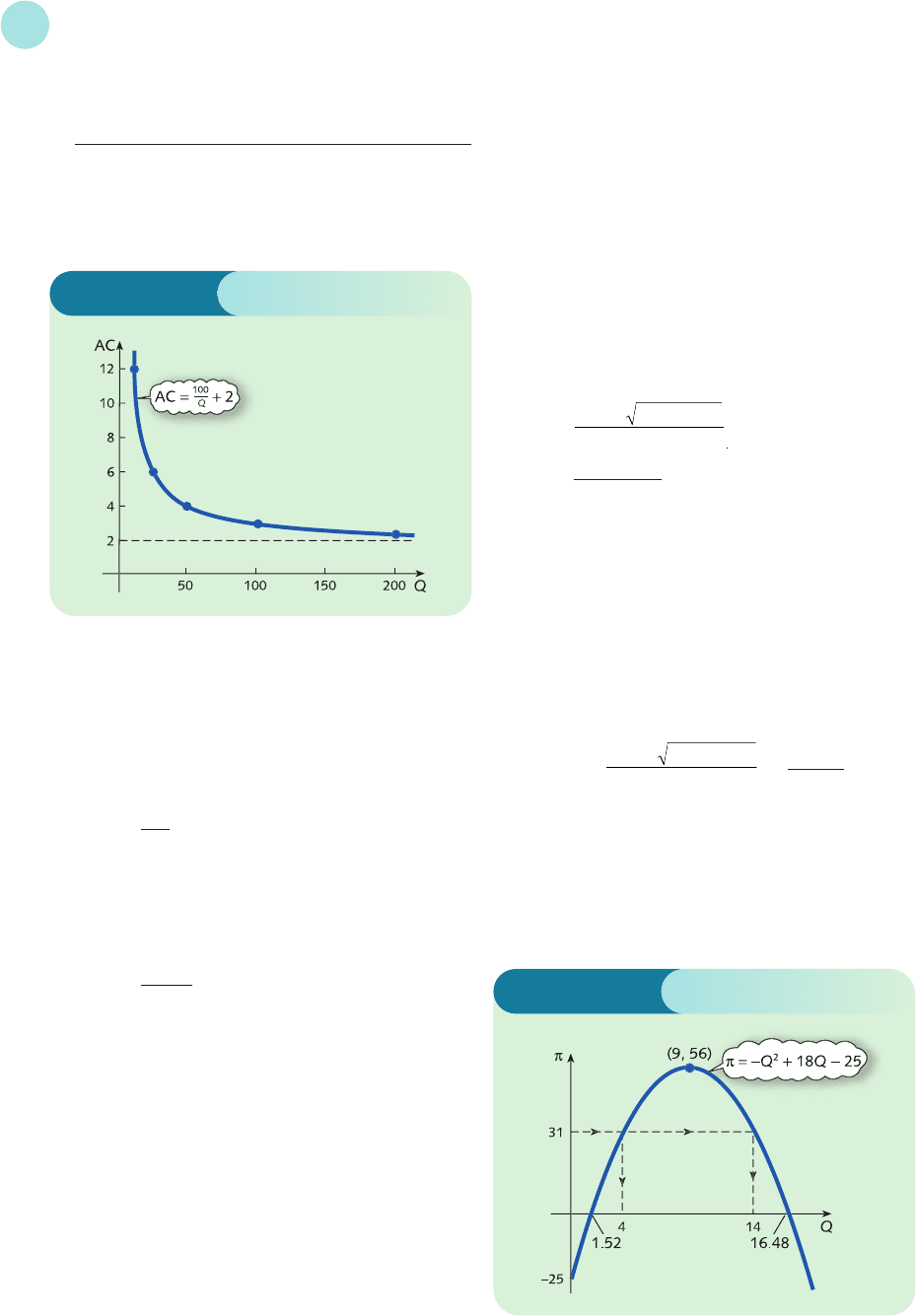
In fact, it is not necessary to plot the tabulated
values if all that is required is a rough sketch. It is
obvious that if a very small number is put into the
AC function then a very large number is produced
because of the term 100/Q. For example, when
Q = 0.1
AC =+2 = 1002
It should also be apparent that if a very large number is
put into the average cost function then the term 100/Q
is insignificant, so AC is approximately 2. For example,
when Q = 10 000
AC =+2 = 2.01
The graph of AC therefore ‘blows up’ near Q = 0 but
settles down to a value just greater than 2 for large Q.
Consequently, the general shape of the graph shown
in Figure S2.9 is to be expected.
3 TC = 25 + 2Q
TR = PQ = (20 − Q)Q = 20Q − Q
2
Hence
π=TR − TC
= (20Q − Q
2
) − (25 + 2Q)
= 20Q − Q
2
− 25 − 2Q
=−Q
2
+ 18Q − 25
100
10 000
100
0.1
Step 1
The coefficient of Q
2
is negative, so the graph has an
inverted U shape.
Step 2
The constant term is −25, so the graph crosses the
vertical axis at −25.
Step 3
The quadratic equation
−Q
2
+ 18Q − 25 = 0
has solutions
Q =
=
so the graph crosses the horizontal axis at Q = 1.52 and
Q = 16.48.
The graph of the profit function is sketched in
Figure S2.10.
(a) If π=31 then we need to solve
−Q
2
+ 18Q − 25 = 31
that is,
−Q
2
+ 18Q − 56 = 0
Q ==−
so Q = 4 and Q = 14.
These values can also be found by drawing a
horizontal line π=31 and then reading off the
corresponding values of Q from the horizontal
axis as shown on Figure S2.10.
18 ± 10
−2
−± −
−
18 324 224
2
( )
−18 ± 14.97
−2
−± −
−
18 324 100
2
( )
Solutions to Problems
614
One possible table of function values for the average
cost function is
Q 10 25 50 100 200
AC 12 6 4 3 2.5
The graph of the average cost function is sketched in
Figure S2.9.
Figure S2.9
Figure S2.10
MFE_Z02.qxd 16/12/2005 10:51 Page 614
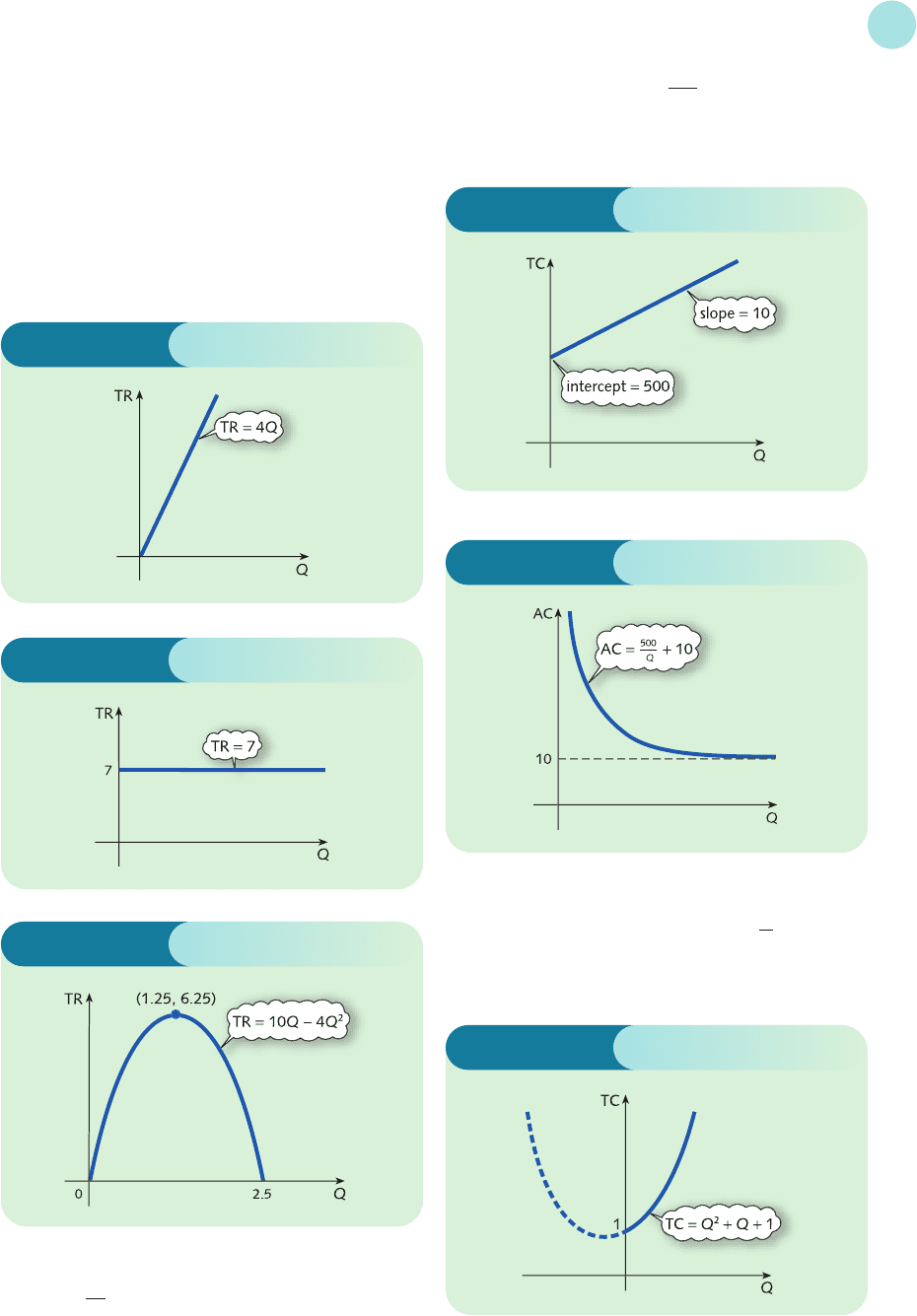
(b) By symmetry the parabola reaches its maximum
halfway between 1.52 and 16.48: that is, at
Q =
1
/
2(1.52 + 16.48) = 9
The corresponding profit is given by
π=−(9)
2
+ 18(9) − 25 = 56
4 (a) 4Q; (b) 7; (c) 10Q − 4Q
2
.
The graphs are sketched in Figures S2.11,
S2.12 and S2.13.
7 TC = Q
2
+ Q + 1; AC = Q + 1 + .
The graphs are sketched in Figures S2.16 and S2.17.
1
Q
Solutions to Problems
615
5 (a) P = 50 − 4Q;
(b) P = .
10
Q
Figure S2.11
Figure S2.12
Figure S2.14
Figure S2.15
Figure S2.16
Figure S2.13
6 TC = 500 + 10Q; AC =+10.
The graphs are sketched in Figures S2.14 and S2.15.
500
Q
MFE_Z02.qxd 16/12/2005 10:51 Page 615
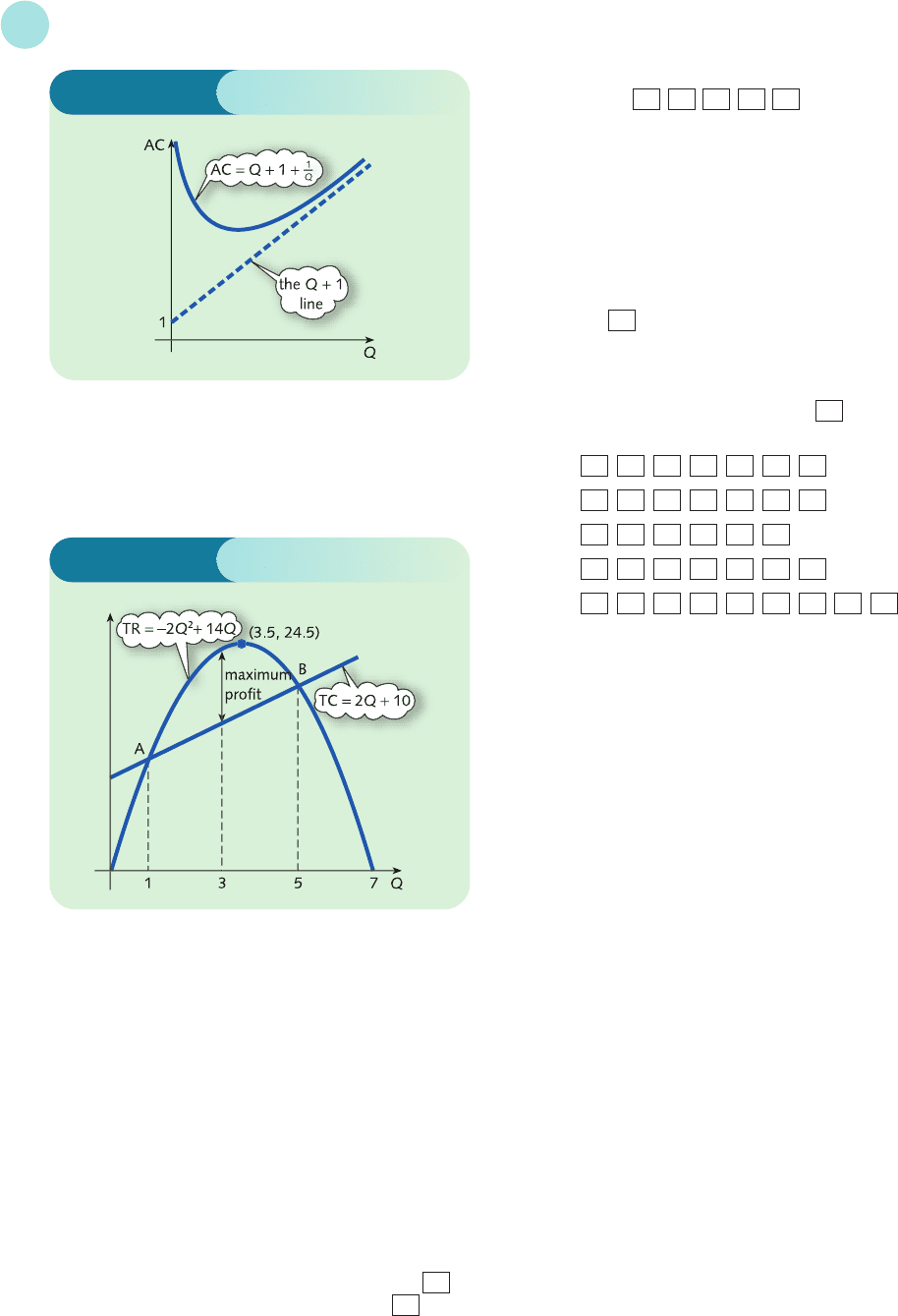
8 π=−2Q
2
+ 20Q − 32; (a) 2, 8; (b) 20; (c) 5.
9 The graphs of TR and TC are sketched in Figure S2.18.
(a) 1, 5; (b) 3.
get the result. For example to calculate 10
2
the key
sequence is 1 0 x
y
2 = .
2 (1) (a) 4, because 4
2
= 16.
(b) 3, because 3
3
= 27.
(c) 32, because 4
5/2
= (4
1/2
)
5
= 2
5
.
(d)
1
/4
, because 8
−2/3
= (8
1/3
)
−2
= 2
−2
= 1/2
2
.
(e) 1, because 1
n
= 1 for any index, n.
(2) Some calculators have a function key (typically
labelled x
1/y
) which can be used to evaluate b
1/n
directly. However, this does not result in any
real reduction in the number of key presses. In
practice, it is just as easy to handle fractional
indices using the ordinary power key x
y
. The
corresponding key sequences are
(a) 16x
y
1
a
b
/c
2 =
(b) 27x
y
1
a
b
/c
3 =
(c) 4 x
y
5
a
b
/c
2 =
(d) 8 x
y
2
a
b
/c
3 ±=
(e) 1 x
y
17
a
b
/c
25±=
3 (a) (x
3/4
)
8
= x
(3/4)×8
= x
6
(rule 3)
(b) x
2
÷ x
3/2
= x
2−(3/2)
= x
1/2
(rule 2)
(c) (x
2
y
4
)
3
= (x
2
)
3
( y
4
)
3
(rule 4)
= x
2×3
y
4×3
(rule 3)
= x
6
y
12
(d) √x(x
5/2
+ y
3
) = x
1/2
(x
5/2
+ y
3
)
(definition of b
1/n
)
= x
1/2
x
5/2
+ x
1/2
y
3
(multiply out the brackets)
= x
(1/2)+(5/2)
+ x
1/2
y
3
(rule 1)
= x
3
+ x
1/2
y
3
The term x
1/2
y
3
cannot be simplified, because
x
1/2
and y
3
have different bases.
4 (a) f (K, L) = 7KL
2
f(λK, λL) = 7(λK)(λL)
2
= 7λK λ
2
L
2
(rule 4)
= (λλ
2
)(7KL
2
)
=λ
3
f(K, L) (rule 1)
Increasing returns to scale because 3 > 1.
(b) f(K, L) = 50K
1/4
L
3/4
f(λK, λL) = 50(λK)
1/4
( λL)
3/4
= 50λ
1/4
K
1/4
λ
3/4
L
3/4
(rule 4)
= (λ
1/4
λ
3/4
)(50K
1/4
L
3/4
)
=λ
1
f(K, L) (rule 1)
Constant returns to scale.
Solutions to Problems
616
10 a + b + c = 9
4a + 2b + c = 34
9a + 3b + c = 19
a =−20, b = 85, c =−56; π=−36
11 1000, 1004.08,..., 1750; 22.8.
12 (a) 5, 30; (b) 18.
Section 2.3
1 (1) (a) 100; (b) 10; (c) 1; (d) 1/10;
(e) 1/100; (f) 1; (g) −1; (h) 1/343;
(i) 81; (j) 72 101; (k) 1.
(2) To evaluate b
n
on a calculator you enter the base,
b, press the power key (typically denoted by x
y
),
enter the power, n, and finally press the = key to
Figure S2.17
Figure S2.18
MFE_Z02.qxd 16/12/2005 10:51 Page 616
5 (1) (a) 3; (b) 2; (c) 1; (d) 0; (e) −1; (f ) −2.
(2) Same as part (1), because if M = 10
n
then
log
10
M = n.
(3) On most calculators there are two logarithm
function keys, log
10
(possibly labelled log or log
10
)
and ln (possibly labelled ln or log
e
). The latter is
known as the natural logarithm and we introduce
this function in the next section. This question
wants you to evaluate logarithms to base 10, so
we use the key log .
Warning: there is no standard layout for the
keyboard of a calculator. It may be necessary for
you first to use the shift key (sometimes called
the inverse function or second function key) to
activate the log
10
function.
6 (a) log
b
+ log
b
z (rule 2)
= log
b
(rule 1)
(b) log
b
x
4
+ log
b
y
2
(rule 3)
= log
b
(x
4
y
2
) (rule 1)
7 (a) 3
x
= 7
log(3
x
) = log 7
(take logarithms of both sides)
x log 3 = log 7
(rule 3)
x =
(divide both sides by log 3)
x =
(using base 10 on a calculator)
x = 1.77
(to two decimal places)
(b) 5(2)
x
= 10
x
log[5(2)
x
] = log(10)
x
(take logarithms of both sides)
log 5 + log(2
x
) = log(10)
x
(rule 1)
log 5 + x log 2 = x log 10
(rule 3)
x(log 10 − log 2) = log 5
(collect terms and factorize)
x log 5 = log 5
(rule 2)
x = 1
(divide both sides by log 5)
0.845 098 040
0.477 121 255
log 7
log 3
D
F
xz
y
A
C
D
F
x
y
A
C
which is, of course, the obvious solution to the
original equation! Did you manage to spot this
for yourself before you started taking logs?
8 (a) 64; (b) 2; (c) 1/3; (d) 1;
(e) 1; (f) 6; (g) 4; (h) 1/343.
9 (a) 8; (b) 1/32; (c) 625; (d) 9/4; (e) 2/3.
10 (a) y
2
; (b) xy
2
; (c) x
4
y
2
; (d) 1;
(e) 2; (f) 5pq
2
.
11 (a) x
−4
; (b) 5x
1/2
; (c) x
−1/2
; (d) 2x
3/2
; (e) 8x
−4/3
.
12 (a) 3600; (b) 200 000.
13 The functions in parts (a) and (b) are homogeneous
of degree 7/12 and 2 respectively, so (a) displays
decreasing returns to scale and (b) displays increasing
returns to scale. The function in part (c) is not
homogeneous.
14 A[b(λK )
α
+ (1 − b)(λL)
α
]
1/α
= A[bλ
α
K
α
+ (1 − b)λ
α
L
α
]
1/α
(rule 4)
= A[(λ
α
)(bK
α
+ (1 − b)L
α
)]
1/α
(factorize)
= A(λ
α
)
1/α
[bK
α
+ (1 − b)L
α
]
1/α
(rule 4)
=λA[bK
α
+ (1 − b)L
α
]
1/α
(rule 3)
so f (λK, λL) =λ
1
f (K, L) as required. This is known as
the constant elasticity of substitution (CES) production
function.
15 (a) 2; (b) −1; (c) −3; (d) 6; (e)
1
/
2; (f)
4
/
3.
16 (a) 2/3; (b) 3; (c)
1
/4.
17 (a) 2; (b) 1; (c) 0; (d)
1
/2; (e) −1.
18 (a) 0; (b) log
b
; (c) log
b
.
19 (a) 2 log
b
x + 3 log
b
y + 4 log
b
z
(b) 4 log
b
x − 2 log
b
y − 5 log
b
z
(c) log
b
x − log
b
y − log
b
z
20 (a) −q; (b) 2p + q; (c) q − 4r; (d) p + q + 2r.
21 (a) 78.31; (b) 1.48; (c) 3; (d) 0.23.
22 (a) x ≤ 0.386 (3 dp)
(b) x > 14.425 (Notice that the inequality is > here.)
23 x = 3 (Note that the second solution of your quadratic,
x =−5 is not valid.)
Section 2.4
1 x −3 −2 −1012 3
3
x
0.04 0.11 0.33 1 3 9 27
3
−x
27 9 3 1 0.33 0.11 0.04
The graphs of 3
x
and 3
−x
are sketched in Figures S2.19
and S2.20 (overleaf) respectively.
1
2
1
2
D
F
x
5
y
z
2
A
C
D
F
x
3
y
2
A
C
Solutions to Problems
617
MFE_Z02.qxd 16/12/2005 10:51 Page 617
2 (a) 2.718 145 927, 2.718 268 237, 2.718 280 469.
(b) 2.718 281 828 ; values in part (a) are getting closer
to that of part (b).
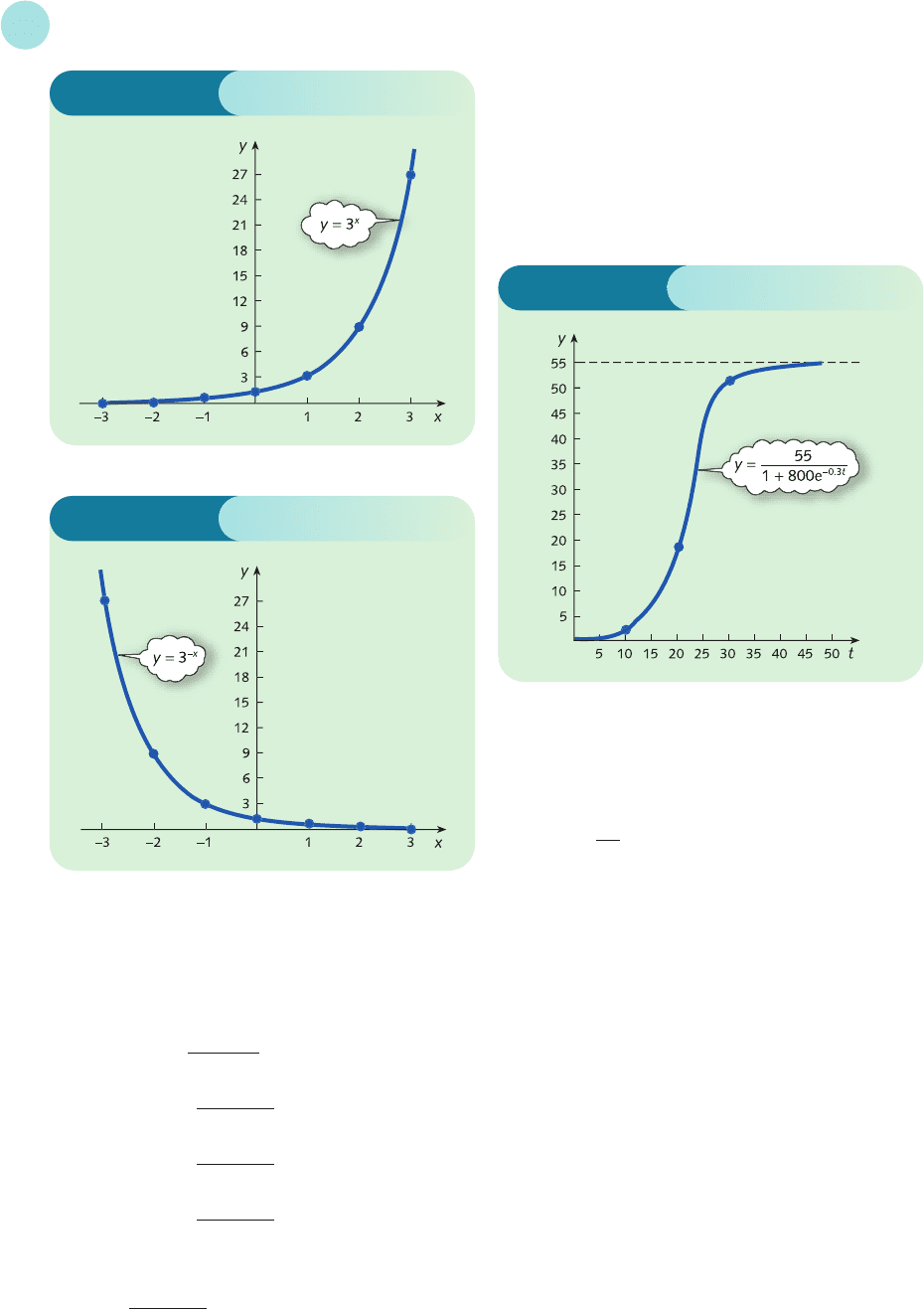
3 (1) Substituting t = 0, 10, 20 and 30 gives
(a) y(0) ==0.07%
(b) y(10) ==1.35%
(c) y(20) ==18.44%
(d) y(30) ==50.06%
(2) As t increases, e
−0.3t
goes to zero, so y approaches
= 55%
55
1 + 800(0)
55
1 + 800e
−9
55
1 + 800e
−6
55
1 + 800e
−3
55
1 + 800e
0
4 (a) ln a
2
+ ln b
3
(rule 1)
= 2 ln a + 3 ln b (rule 3)
(b) ln x
1/2
− ln y
3
(rule 3)
= ln (rule 2)
5 (a) Putting t = 0 and 2 into the expression for TR gives
TR = 5e
0
= $5 million
TR = 5e
−0.3
= $3.7 million
(b) To solve 5e
−0.15t
= 2.7 we divide by 5 to get
e
−0.15t
= 0.54 and then take natural logarithms,
which gives
−0.15t = ln(0.54) =−0.62
Hence t = 4 years.
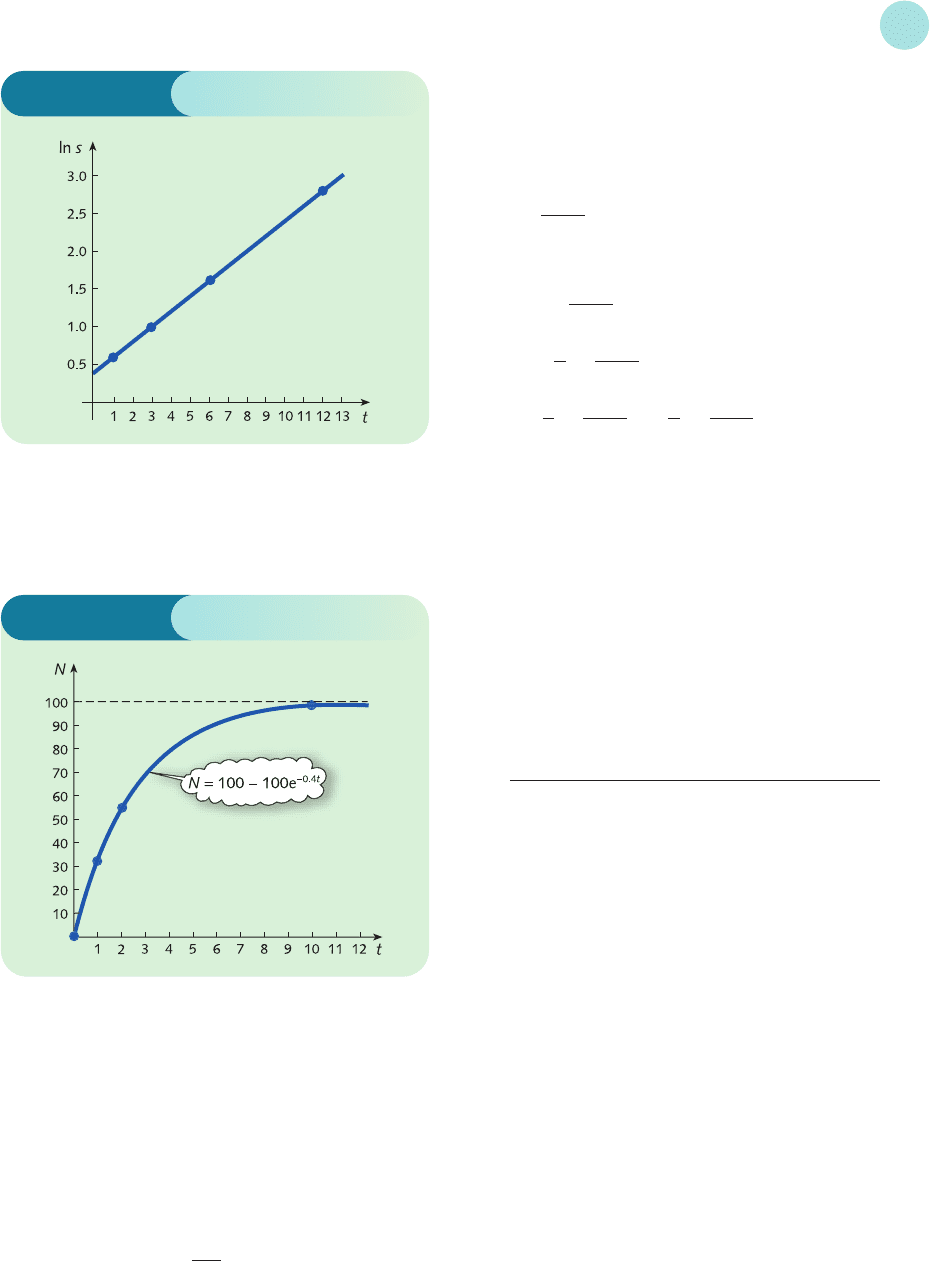
6 (1) Missing numbers are 0.99 and 2.80.
(2) The graph is sketched in Figure S2.22.
Intercept, 0.41; slope, 0.20.
(3) A = 0.2, B = e
0.41
= 1.5.
(4) (a) 9100; (b) 2.4 × 10
8
; answer to part (b) is
unreliable since t = 60 is well outside the range
of given data.
D
F
x
1/2
y
3
A
C
Solutions to Problems
618
Figure S2.19
Figure S2.21
Figure S2.20
(3) A graph of y against t, based on the information
obtained in parts (1) and (2), is sketched in
Figure S2.21. This shows that, after a slow start,
camcorder ownership grows rapidly between
t = 10 and 30. However, the rate of growth then
decreases as the market approaches its saturation
level of 55%.
MFE_Z02.qxd 16/12/2005 10:51 Page 618
7 (1) (a) 33; (b) 55; (c) 98.
(2) 100.
(3) The graph of N against t is sketched in Figure S2.23.
11 A = 50 000, a = 0.137; (a) $25 205; (b) $0.
12 The equation
N = c(1 − e
−kt
) = c − ce
−kt
rearranges as
e
−kt
=
Taking logarithms gives
−kt = ln
t =− ln
= ln
−1
= ln
(a) 350 000.
(b) 60 days.
(c) Market saturation level is 700 000, which is less
than the three-quarters of a million copies needed
to make a profit, so the proprietor should sell.
13 Putting y = ln Q, x = ln K gives
y =
1
/
3
x + (ln 3 +
1
/
2 ln L)
which is of the form ‘y = ax + b’.
Slope =
1
/3, intercept = ln 3 +
1
/2 ln L.
14 (a) ln Q = ln(AL
n
) = ln A + ln L
n
= ln A + n ln L.
(b) ln L 0 0.69 1.10 1.39 1.61
ln Q −0.69 −0.46 −0.33 −0.22 −0.16
(c) n = 0.34, A = 0.50.
15 All five graphs are increasing throughout.
Graphs of x
2
, x
3
and e
x
bend upwards, i.e. the slope
increases with increasing x, whereas x has a constant
slope and √x has a decreasing slope.
With the exception of e
x
, all graphs pass through
(0, 0) and (1, 1). On 0 < x < 1, x
3
< x
2
< x <√x whereas
on x > 1 the order is reversed.
16 All five graphs have the same basic shape and pass
through (1, 0).
On 0.2 < x < 1, ln x < log
6
x < log
10
x whereas on
x > 1, the order is reversed.
17 (a) P − 100 =−
2
/3Q
n
(subtract 100 from both sides)
−
3
/2 (P − 100) = Q
n
(divide both sides by −
2
/3)
150 − 1.5P = Q
n
(multiply out the brackets)
ln(150 − 1.5P) = ln(Q
n
) = nln Q
(take logs and use rule 3)
which is of the form y = ax + b with a = n and b = 0.
D
F
c
c − N
A
C
1
k
D
F
c − N
c
A
C
1
k
D
F
c − N
c
A
C
1
k
D
F
c − N
c
A
C
c − N
c
Solutions to Problems
619
The graph sketched in Figure S2.23 is called a
learning curve. It shows that immediately after
training the worker can produce only a small
number of items. However, with practice, output
quickly increases and finally settles down at a daily
rate of 100 items.
8 (a) ln x + ln y; (b) ln x + 4 ln y; (c) 2 ln x + 2 ln y;
(d) 5 ln x − 7 ln y; (e)
1
/
2
ln x −
1
/
2
ln y;
(f)
1
/2 ln x +
3
/2 ln y −
1
/2 ln z.
9 (a) ln x
3
; (b) ln .
10 (a) 1.77; (b) −0.80; (c) no solution;
(d) 0.87; (e) 0.22; (f) 0.35.
D
F
x
4
z
5
x
3
A
C
Figure S2.22
Figure S2.23
MFE_Z02.qxd 16/12/2005 10:51 Page 619
