Исаев Ю.Н., Колчанова В.А., Хохлова Т.Е., Васильева О.В. Курс лекций по теоретической электротехнике

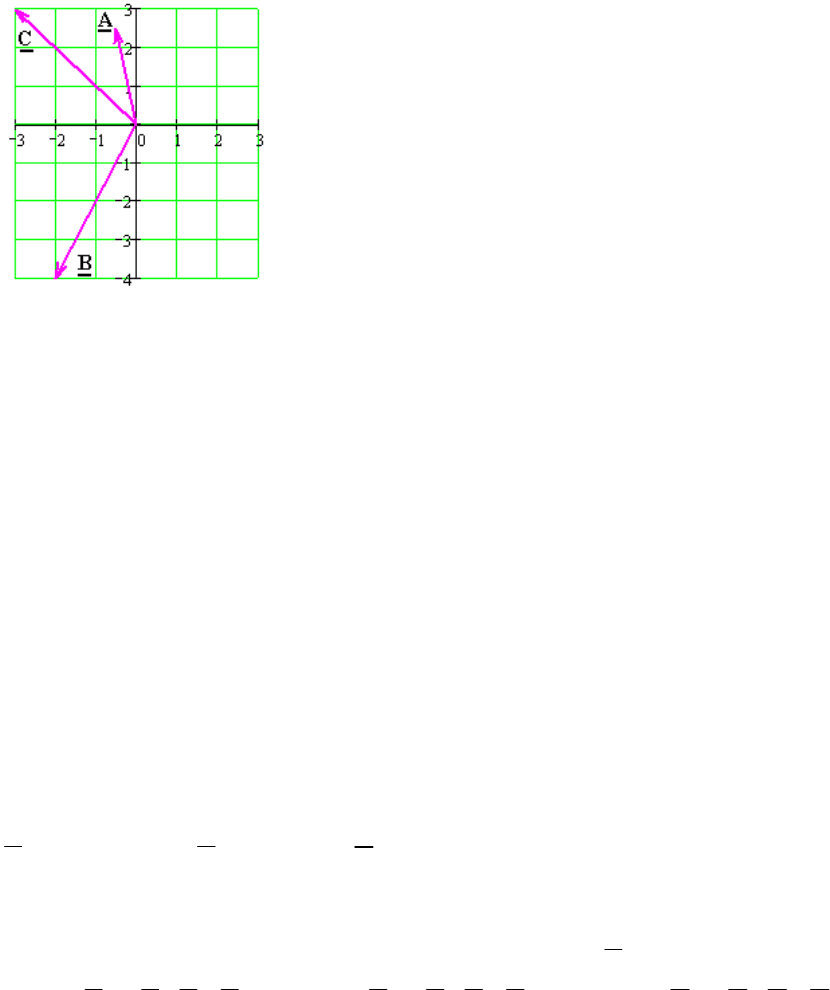
81

3.1. Метод симметричных составляющих

Расчет симметричных режимов гораздо

проще несимметричных, поэтому для расчета

несимметричных (несбалансированных) ре-

жимов в трехфазных цепях широко применя-

ется метод симметричных составляющих

(МСС).

Метод симметричных составляющих от-

носится к специальным методам расчета трех-

фазных цепей и широко применяется для ана-

лиза несимметричных режимов их работы, в

том числе с нестатической

нагрузкой. В осно-

ве метода лежит представление несимметричной трехфазной системы

переменных (ЭДС, токов, напряжений и т.п.) в виде суммы трех сим-

метричных систем, которые называют симметричными составляющими.

Различают симметричные составляющие прямой, обратной и нулевой

последовательностей, которые различаются порядком чередования фаз.

Он основан на представлении любой трехфазной несимметричной

системы величин (трех векторов) в виде суммы трех симметричных

систем величин.

Эти симметричные системы, которые в совокупности

образуют несимметричную систему величин, называются ее симмет-

ричными составляющими. Симметричные составляющие отличаются

друг от друга порядком следования (чередования) фаз. Они

называют-

ся системами прямой, обратной и нулевой последовательностей.

Любая не симметричная система векторов однозначно раскладывает-

ся на симметричные составляющие

Пример: Пусть имеется трехфазная система векторов (рис. 3.7):

0,5 2,5; 2 4; 3 3.

A

jB jC j     

Разложим её на симметричные составляющие. В результате разложения

каждый из векторов будет иметь свои компоненты прямой обратной и

нулевой последовательностей. Например, вектор

A

будет иметь компо-

ненты





123

,,

A

AA A , вектор





123

,,

B

BB B



и вектор





123

,,CCCC

Чередование фаз в прямой последовательности и связь между

компонентами векторов будет следующей

2/3 2/3

111 11

,,

jj

AB Ae C Ae





.

Чередование фаз в обратной последовательности

2/3 2/3

222 22

,,

jj

AB Ae C Ae





.

В нулевой последовательности все компоненты векторов равны

Рис. 3.7

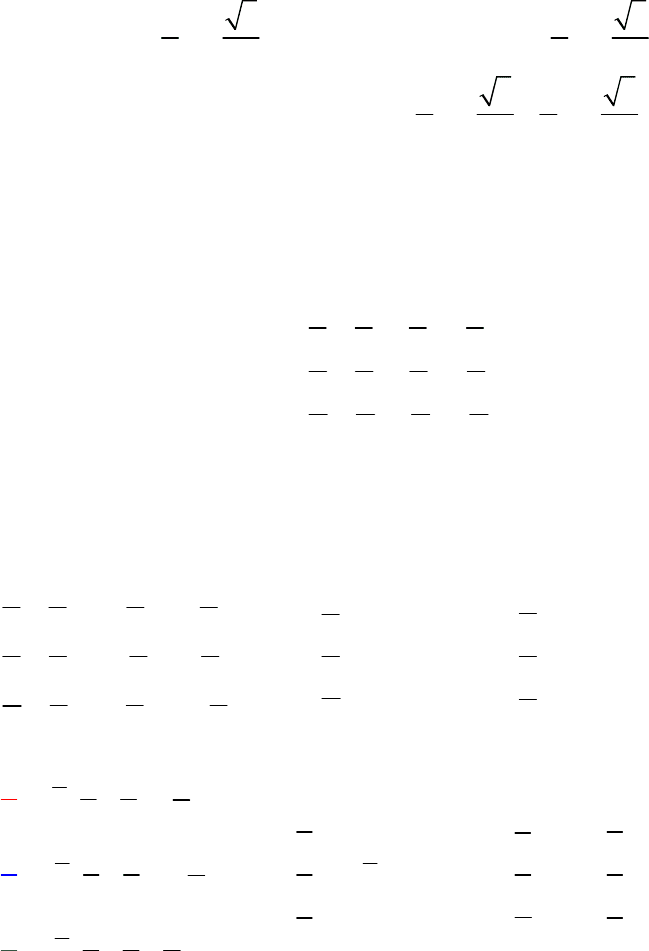
82

000

,

A

BC



 .

Полезно ввести обозначение для фазового множителя:

2/3 2

13 13

0,5 0,866 , 0,5 0,866

22 22

j

ae j j a j j



       .

Заметим, что

2

1313

11 0.

2222

aa j j  

Каждый из

векторов несимметричной системы раскладывается по компонентам

прямой обратной и нулевой последовательности.

120

;

..

;

.

AA A A

B

Обр

BBB

CC C

Н

ул

р

т

C

а

П

ям





Или если использовать фазовый множитель и в качестве

основной

фазы

выбрать фазу

A

это выражение можно переписать:

120

1

22

120 2

2

0

12 0

. .

1

.

11

AA A A

A

BAa AaA B aa

Н

у

П

рям

A

C

A

aa

CAa Aa

л

A

Обрат











 









 





  

Если обернуть это матричное выражение то можно получить:



2

11

22

00

2

0

1

3

1

2,687 1, 289

11

1 1, 354 0,711

33

111 1,833 0,5

1

3

ABaCa

aa

AA

Aj

ABa Ca A aa B A j

Cj

AA

AB

A

CA











 

  







 

  

     





 

  



  



 





  

 











.

83

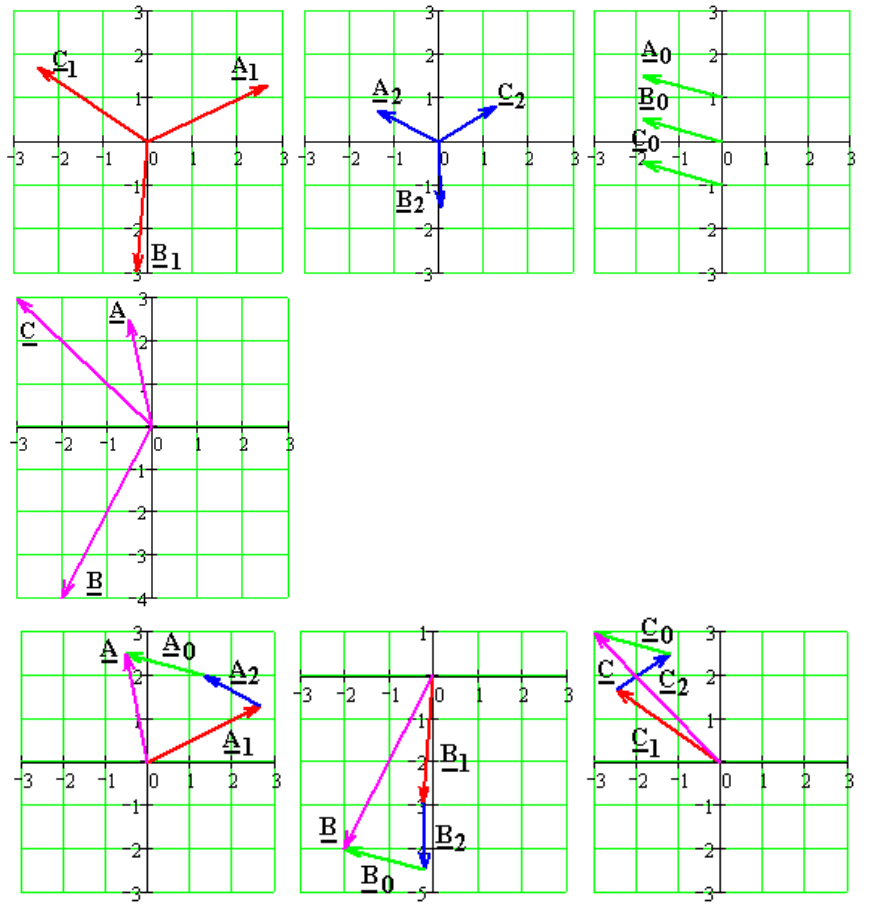
Последовательности

Прямая Обратная Нулевая

Рис. 3.8. Результаты разложения трёх векторов А, В, С

на симметричные составляющие

84

При использовании МСС возникает вопрос, что конкретно мы со-

бираемся раскладывать на симметричные составляющие. Если в систе-

ме действует несимметричная системы ЭДС, а цепь сама симметрич-

ная, то нужно раскладывать систему ЭДС. Если действующая система

ЭДС симметричная, а электрическая цепь имеет локальную несиммет-

рию, то нужно раскладывать на симметричные составляющие ток

или

напряжения локального участка.

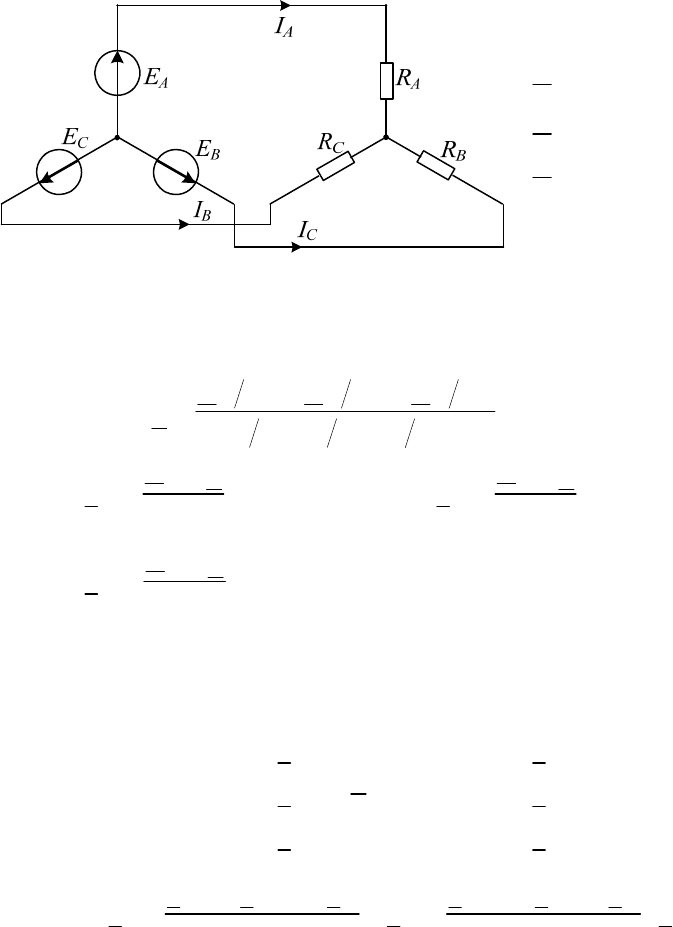
Рассмотрим

пример (рис. 3.9). Пусть задана симметричная система ЭДС

с несимметричной нагрузкой:

120

2

0,5 0,866,

220 B,

220 ,

10Ом,

20Ом,30Ом

j

A

B

C

A

BC

ae j

E

Ea

R

RR









Рис. 3.9

Определим токи методом узловых потенциалов:

70 17,321B

111

ABC

ER ER ER

j

RRR



  



,

15 1,732 A, 9 8,66A,

66,928A.

AB

C

EE

IjI j

RR

E

Ij

R





 





Определим симметричные составляющие. Так как нет нулевого

провода, то нулевая последовательность будет отсутствовать:

2

1

2

0

1

3

111

A

B

C

aa

I

aa I

I



  



  





  



  



  



,

22

122

,,0

33

AB C A BC

IaIaI IaIaI

III

  



.

Далее представлен пример расчета в MathCAD.

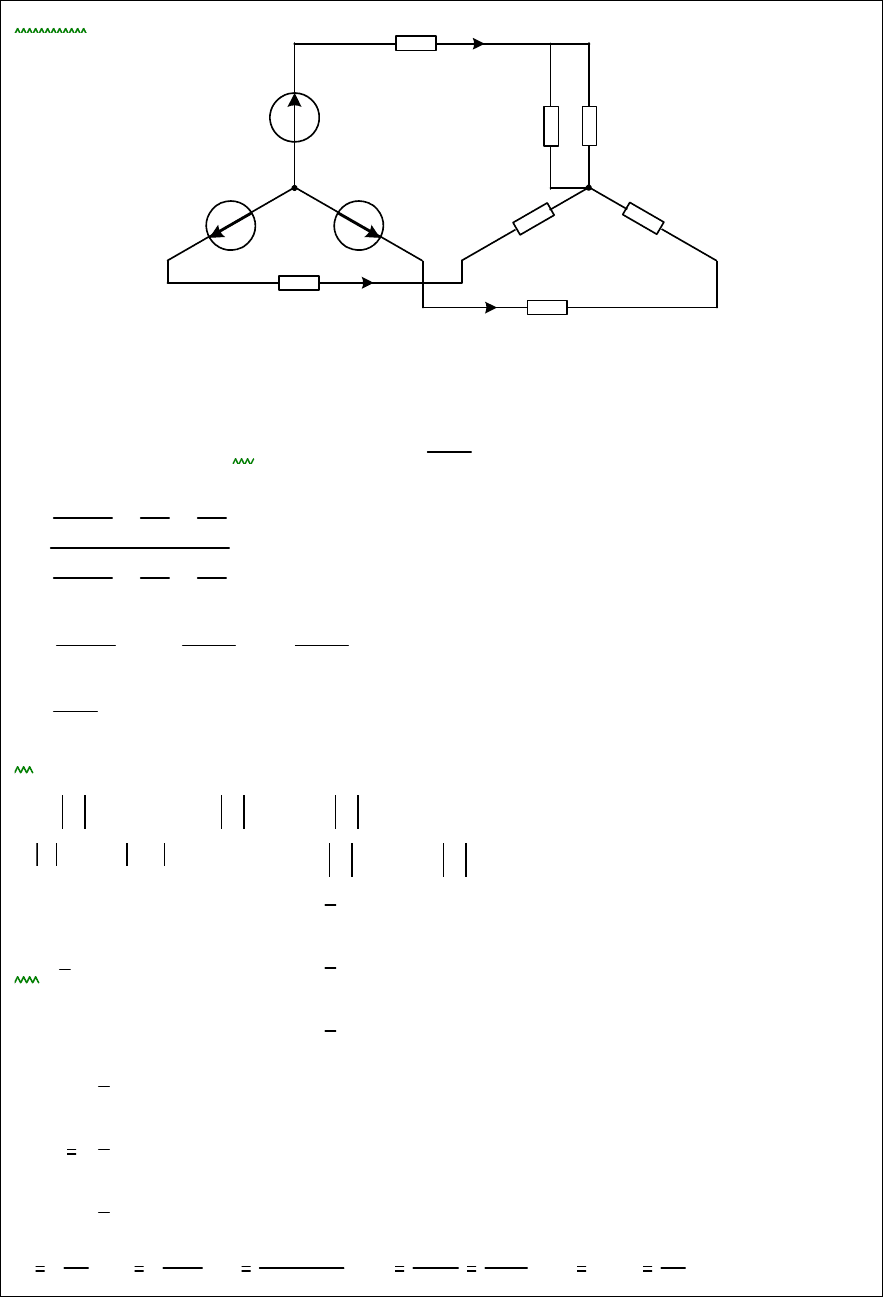
85

Рис. 3.10

ORIGIN 1

E

A

E

C

E

B

R

A

R

C

R

B

R

r

A

I

A

I

B

I

C

Ua 100

ae

i 120 de

g

EUaUaa

2

Ua a

T

R 2

0

r

5

Ra

Rr

E

1

Ra R

E

2

R2

E

3

R2

1

Ra R

1

R2

1

R2

18.182

I

1

E

1

Ra R

I

2

E

2

R2

I

3

E

3

R2

I

T

3.409 1.705 2.165i 1.705 2.165i ()

Ir

I

1

R

Rr

Ir 2.727

I_R I

1

I

r

I_R 0.682

S

I

1

E

1

I

2

E

2

I

3

E

3

S 886.364

PI

1

2

Ra R () I

2

R 2 I

3

2

R

2

P 886.364

Ir

2

r I_R

2

R I

1

2

R

I

2

R 2 I

3

2

R 2 886.364

A

1

3

1

a

2

a

1

a

2

1

A

I_r

0

1

3

I_r

1

3

I_r

1

3

I_r

I1

I2

I0

1

3

Ir

1

3

Ir

1

3

Ir

I0

U0

R

I2

2U2

R

I1

Ua 2 U1

R

U2

I2 R

2

Ir R

32

U0 I0 R

Ir

3

R

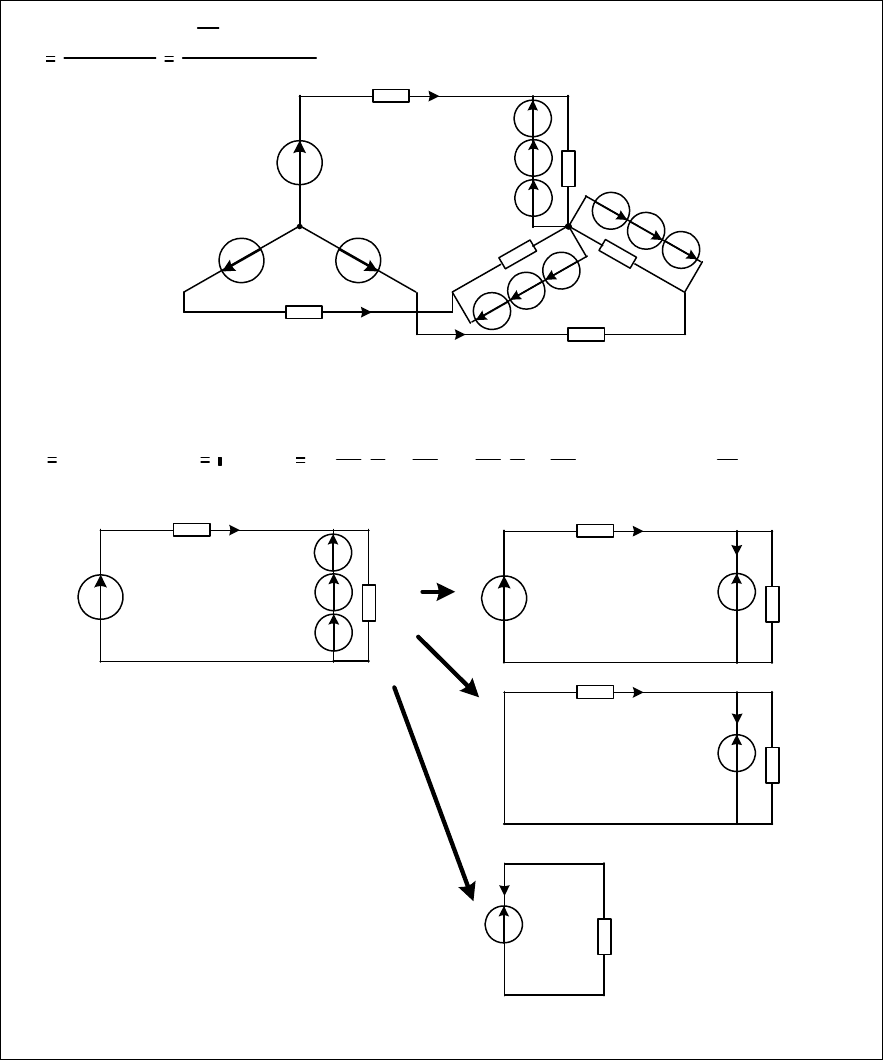
86

Рис. 3.11

Рис. 3.12

U1

I1 R Ua

2

1

3

Ir R

Ua

2

U

1

U

2

U

0

U

1

U

2

U

0

E

A

E

C

E

B

R

A

R

C

R

B

R

I

A

I

B

I

C

U

1

U

2

U

0

Ir r U1 U2 U0 ()

I_r r

I_r

3

R

2

Ua

2

I_r

3

R

2

I_r

3

R solve I_r

30

11

2.727

E

A

R

A

R

I

A

U

1

U

2

U

0

R

A

R

I

A2

U

2

E

A

R

A

R

I

A1

U

1

R

A

U

0

I

1

I

2

I

0

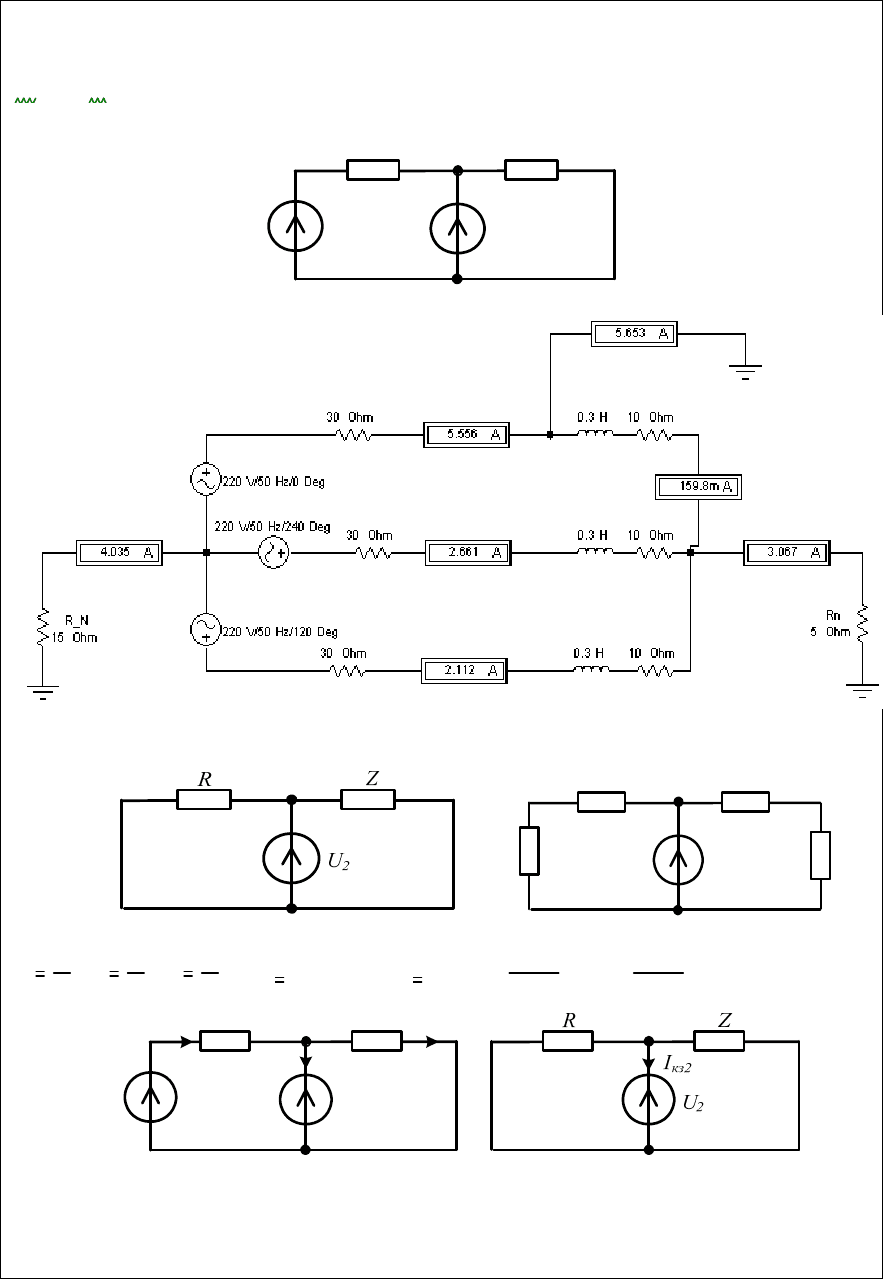
87

Е

Z

R

U

1

Рис. 3.13

Рис. 3.14

Схема обратной последовательности Схема нулевой последовательности

Z

R

U

0

3R

N

3R

n

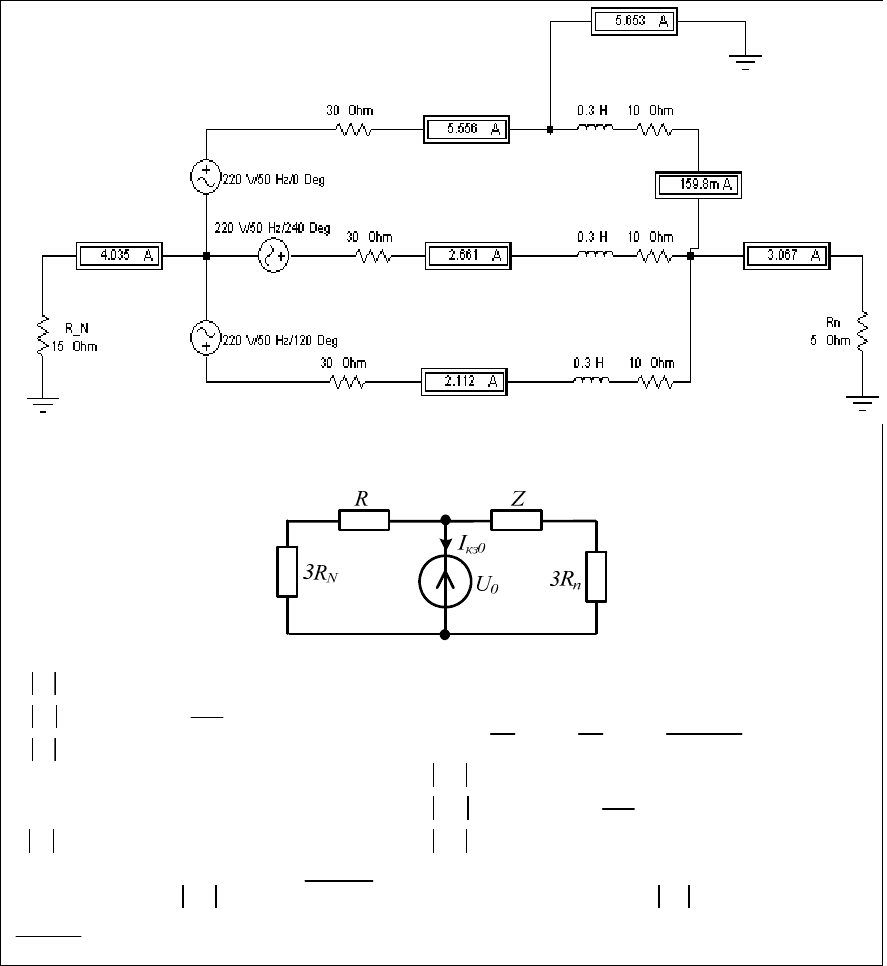
Рис. 3.15 Рис. 3.16

Е

Z

R

U

1

I

An

I

A

I

кз1

Рис. 3.17 Рис. 3.18

ae

i 120 de

g

Ea 22

0

Eb a

2

E

a

Ec a E

a

R

3

0

L 0.

3

100 r1

0

X

L

Zri

X

RN 1

5

Rn

5

Схема прямой последовательности

I

1

Ik

3

I

2

Ik

3

I

0

Ik

3

Ua U

1

U

2

U

0

Ee

Ea Z

ZR

Ze

RZ

ZR

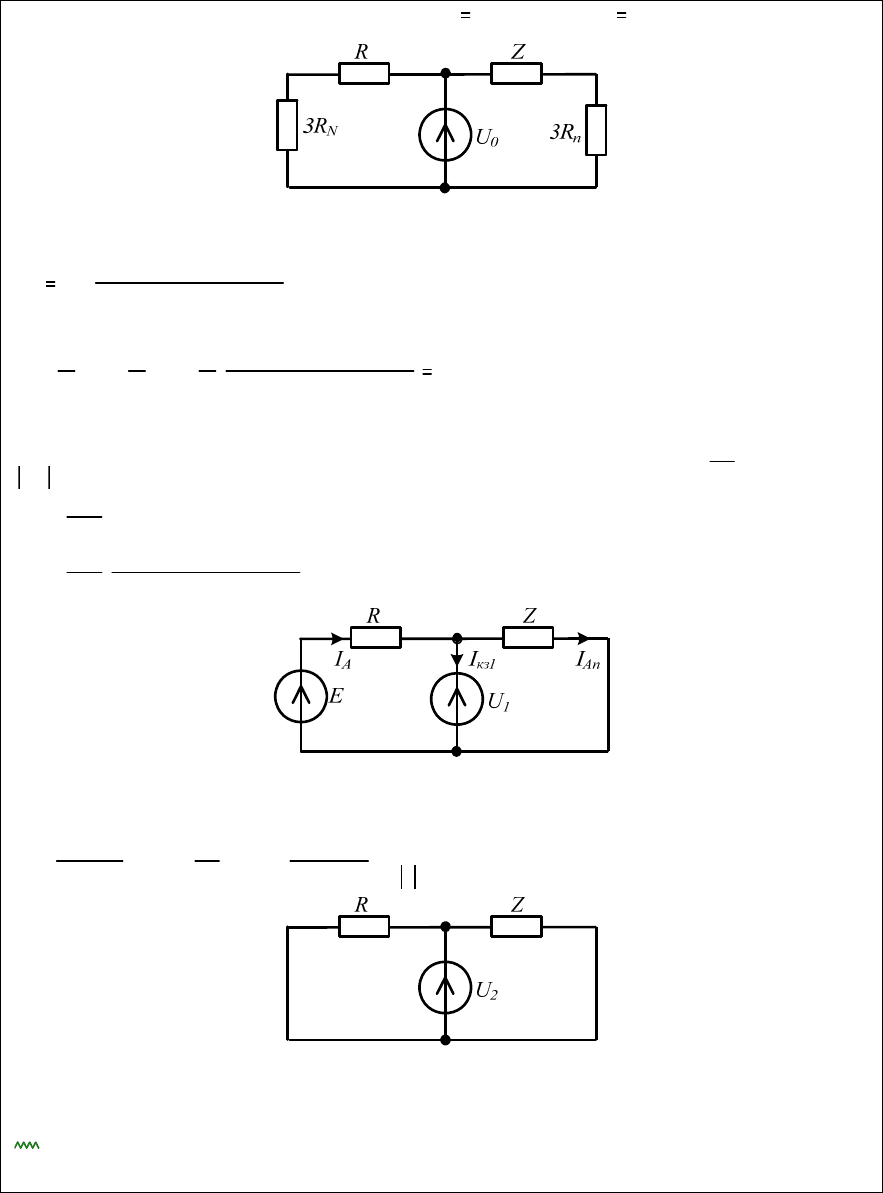
88

Рис. 3.19

Рис. 3.20

Рис. 3.21

Ze 26.566 8.092i Ee 194.816 59.34i

U

1

Ee I

1

Z

e

U

2

I

2

Z

e

U

0

I

0

R3RN ()Z3Rn ()

R3RN Z 3Rn

Ik

0

Give

n

Ee

Ik

3

Ze

Ik

3

Ze

Ik

3

R3RN ()Z3Rn()

R3RN Z 3Rn

0

Ikz Find Ik()

Ikz

5.665 Ikz 5.619 0.719i

com Ikz()

5.665

5.619

7.29

0.719

U

1

Ee

Ikz

3

Z

e

U

2

Ikz

3

Z

e

U

0

Ikz

3

R3RN ()Z3Rn ()

R3RN Z 3Rn

U

T

91.414 41.757i 143.115 50.548i 51.701 8.791i ()

I

1

Ea U

1

R

I

2

U

2

R

I

0

U

0

R3RN

I

T

1.34 3.067 1.748()

A

1

a

2

a

1

a

2

Ia

Ib

Ic

A

I

89

Рис. 3.22

Рис. 3.23

Ia

Ib

Ic

5.568

2.689

2.131

1

deg

arg Ia()

arg Ib()

arg Ic()

8.63

168.73

68.28

I_

1

U

1

Z

I_

2

U

2

Z

I_

0

U

0

Z3Rn

I_

T

1.031 1.601 0.553()

Ina

Inb

Inc

AI

_

Ina

Inb

Inc

0.163

2.689

2.131

1

deg

arg Ina()

arg Inb()

arg Inc()

134.54

168.73

68.28

IrN Ia Ib I

c

IrN 4.02

arg IrN()

deg

24.55

Irn Ina Inb In

c

Irn 3.092

arg Irn()

deg

129.41

90

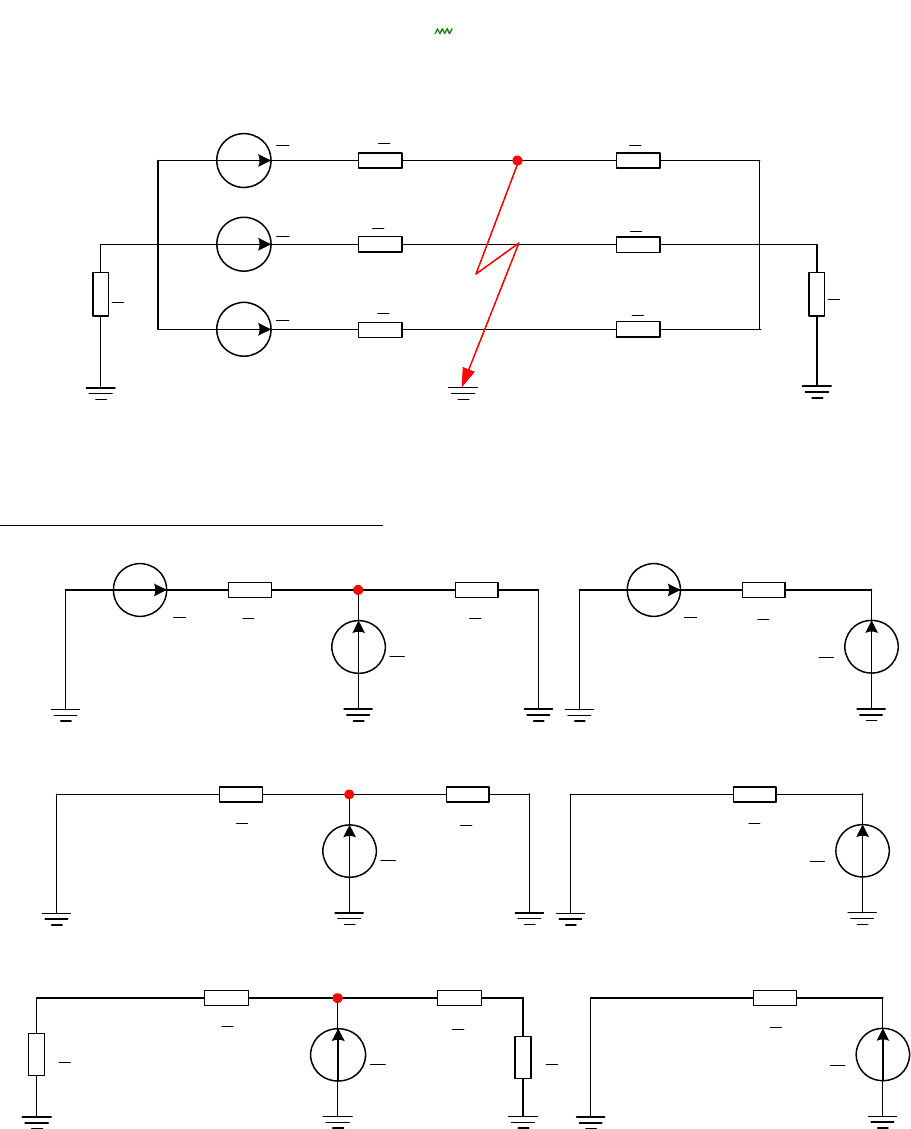
§3.2. Примеры расчёта несимметричных режимов

Поперечная несимметрия (замыкание фазы А на землю)

Пример расчета в MathCAD

E 220 100 L 0.3 XL

r5 L

N

0.032 L

n

0.016 Z

A

riX z

a

j

X

Z

N

j L

N

Z

n

j L

n

Z

N

10.053i Z

n

5.027i

Рис. 3.24

Комплексные схемы замещения

Пряма последовательность

Рис. 3.25

Обратная последовательность

Рис. 3.26

Нулевая последовательность

E

A

E

B

E

C

Z

a

Z

A

Z

B

Z

C

Z

nZ

N

Z

b

Z

c

L

N

3 0.096

L

n

3 0.048

E

A

Z

a

Z

A

U

1

E

Э

Z

Э

U

1

Z

a

Z

A

U

2

Z

Э

U

2

Z

a Z

A

U

0

3Z

N

3Z

n

Z

0

U

0

Исаев Ю.Н., Колчанова В.А., Хохлова Т.Е., Васильева О.В. Курс лекций по теоретической электротехнике

Подождите немного. Документ загружается.