Исаев Ю.Н., Колчанова В.А., Хохлова Т.Е., Васильева О.В. Курс лекций по теоретической электротехнике
Подождите немного. Документ загружается.

61
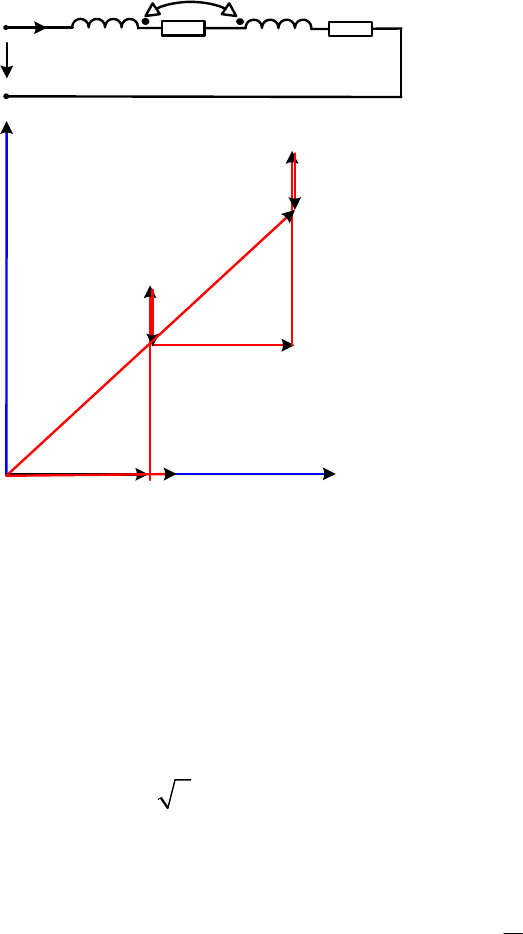
2. По оси
x
в масштабе тока [/ ]
I
M
А
см откладываем значение
тока в цепи
I
. Затем, относительно тока строим топографическую диа-
грамму напряжений. Напряжение
откладываем в масштабе напря-
жения [/ ]
U
M
В
см . Напряжение
1R
U
совпадает по фазе с током
I
.
Напряжение
1
L
U опережает ток на
90 градусов. Затем напряжение
взаимной индукции
M
U отстает
от тока на 90 градусов, потому
что мы имеем встречное включе-
ние, при этом взаимные потоки
вычитаются. Далее откладываем
напряжение
2R
U
на сопротивле-
нии
2
R
совпадающее по фазе с
током
I
. Затем откладываем на-
пряжение
2
L
U опережающее ток
на 90 градусов. И наконец, откла-
дываем напряжение взаимной ин-
дуктивности
M
U , отстающее от
тока на 90 градусов.
§2.8. Расчет цепи с магнитно-связанными индуктивностями
Рассмотрим цепь с магнитно-связанными катушками индуктивно-
сти. Данные цепи таковы:
12
6
( ) 40 2 sin( 45 )В,50Гц,20Ом,
0,1 , 0, 2 , 0,15Гн,
60 10 мкФ.
et t f R
M Гн L Гн L
C
Определим величины
12
,,,,
LL MC
XX XXE
M
L
1
L
2
U(t)
i(t)
R
1
R
2
U
R1
U
L1
U
L2
U
R2
U
M
U
M
I
Рис. 2.21
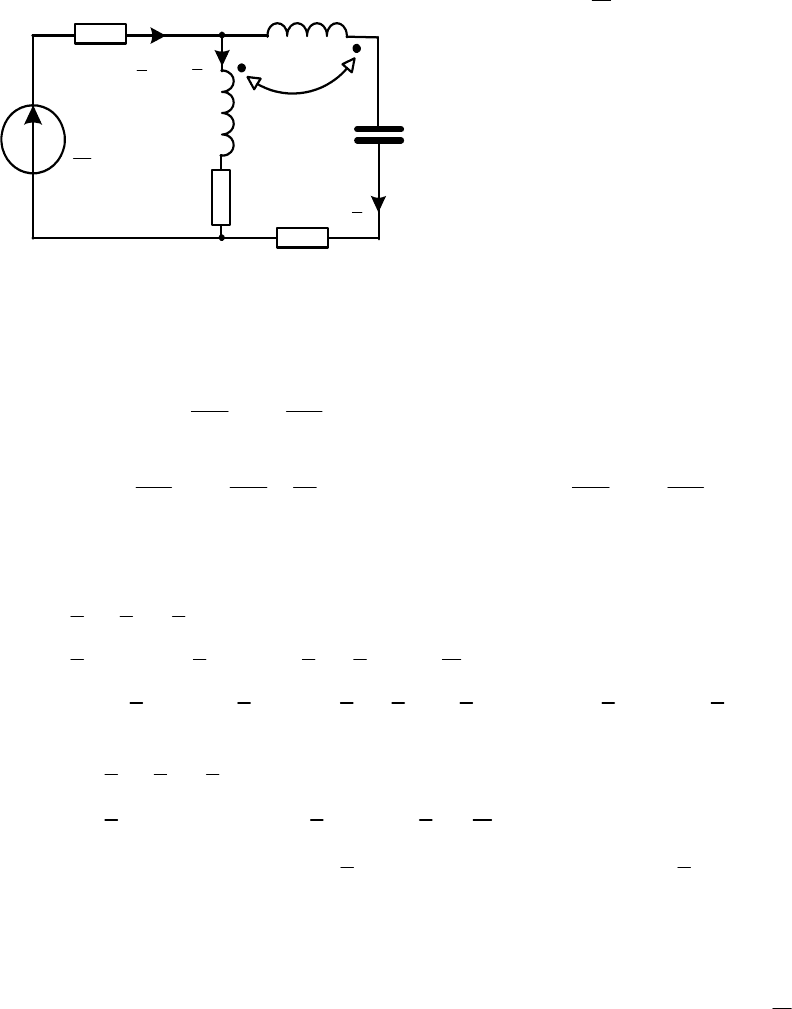
62
11
45
22
31,416 Ом,62,832Ом,
47,124 Ом,53,052Ом,40В.
ML
j
LC
XM XL
XL X Ee
Запишем законы Кирхгофа,
с помощью которых определяются
токи и напряжения в цепи. Запи-
шем эти уравнения для мгновен-
ных значений токов и напряже-
ний, а затем перепишем их для
комплексных – действующих зна-
чений.
В соответствии с представленной схемой имеем.
123
3
2
11 2
33
22
23321
0;
2();
1
20.
ii i
di
di
iR L M i R et
dt dt
di di
di di
LM idtiRiRLM
dt dt C dt dt
Перепишем это уравнение в символической форме:
123
1
1232
21
32332 23
0;
2;
20.
LM
LMC LM
III
IR jX I jX I I R E
jX I jX I jX I I R I R jX I jX I
Приведем подобные члены и упорядочим в матричном виде:
123
1
123
12
23
0;
2;
20.
LM
LM L MC
II I
IR R jX I jX I E
RjX jX I RjX jX jX I
Теперь можно записать матричное уравнение
1
12
11 1
0
2
,
02
0
AB
LM
LM L MC
R R jX jX
E
RjX X RjX X X
.
Поставим данные и получим
M
L
1
2R
C
E
R
I
2
I
1
I
3
L
2
R
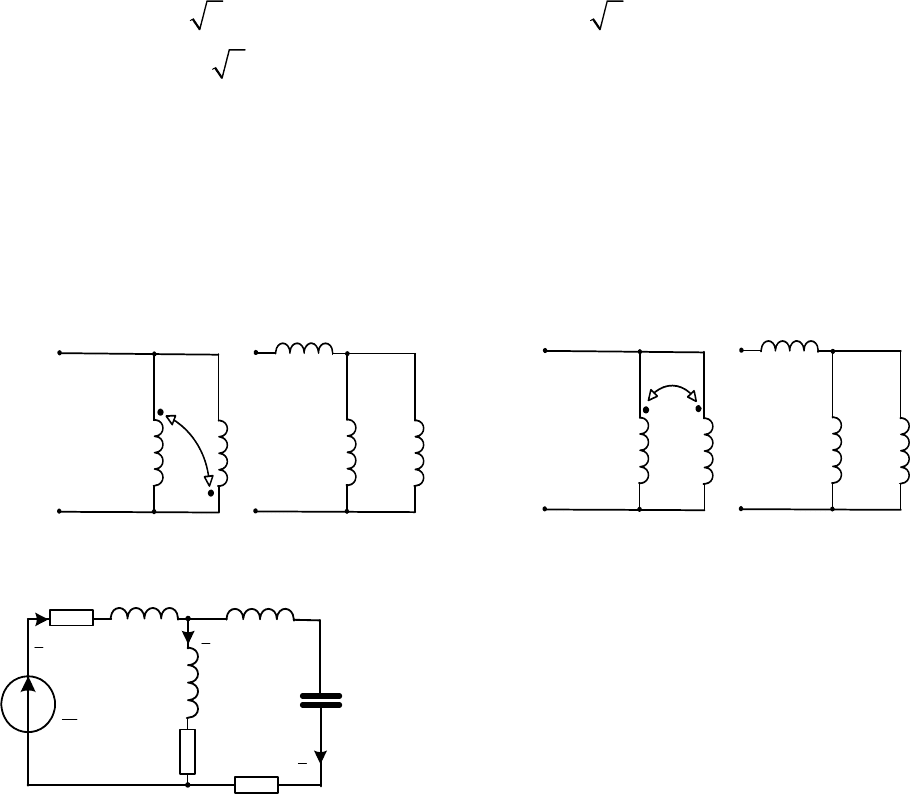
Рис. 2.22
63
L
1
L
2
M
L
1
-M
L
2
-M
M
L
1
L
2
M
L
1
+M L
2
+M
-M
11 1 0
20 40 62,832 31, 416 , 28,284 28, 284
04094,2482025,488 0
A Β
j
jj
jj
.
62,921
151,416
66,539
1,118
0,509 0,996
0,169 0, 211 0, 271
0,34 0,784
0,855
AI B I A B
j
j
j
e
j
je
j
e
.
По полученным результатам запишем мгновенное значения токов
в ветвях
12
3
( ) 1,11 2 sin( 62,921)A, ( ) 0,271 2 sin( 51,416)A,
( ) 0,855 2 sin( 66,539)A.
it t i t t
it t
Использование других методов расчета таких как метод узловых
потенциалов, метод контурных токов затрудняется из-за наличия ин-
дуктивной связи, поэтому исходную схему упрощают, производя раз-
вязку индуктивной связи. Пример развязки индуктивной связи приве-
ден на рис. 2.23. Следует обратить внимание на то, что на рис. нет на-
правлений
токов поэтому нет смысла говорить о встречном или соглас-
ном соединении.
Рис. 2.23
В нашем случае схема развяжет-
ся как указанно на рис. 2.24. Теперь
можно использовать любой известный
метод расчета. Наиболее рациональ-
ным методом расчета в данном случае
будет метод узловых потенциалов.
Определим эквивалентные сопротив-
ления ветвей схемы.
L
1
+M
2R
C
E
R
I
2
I
1
I
3
R
L
2
+M
-M
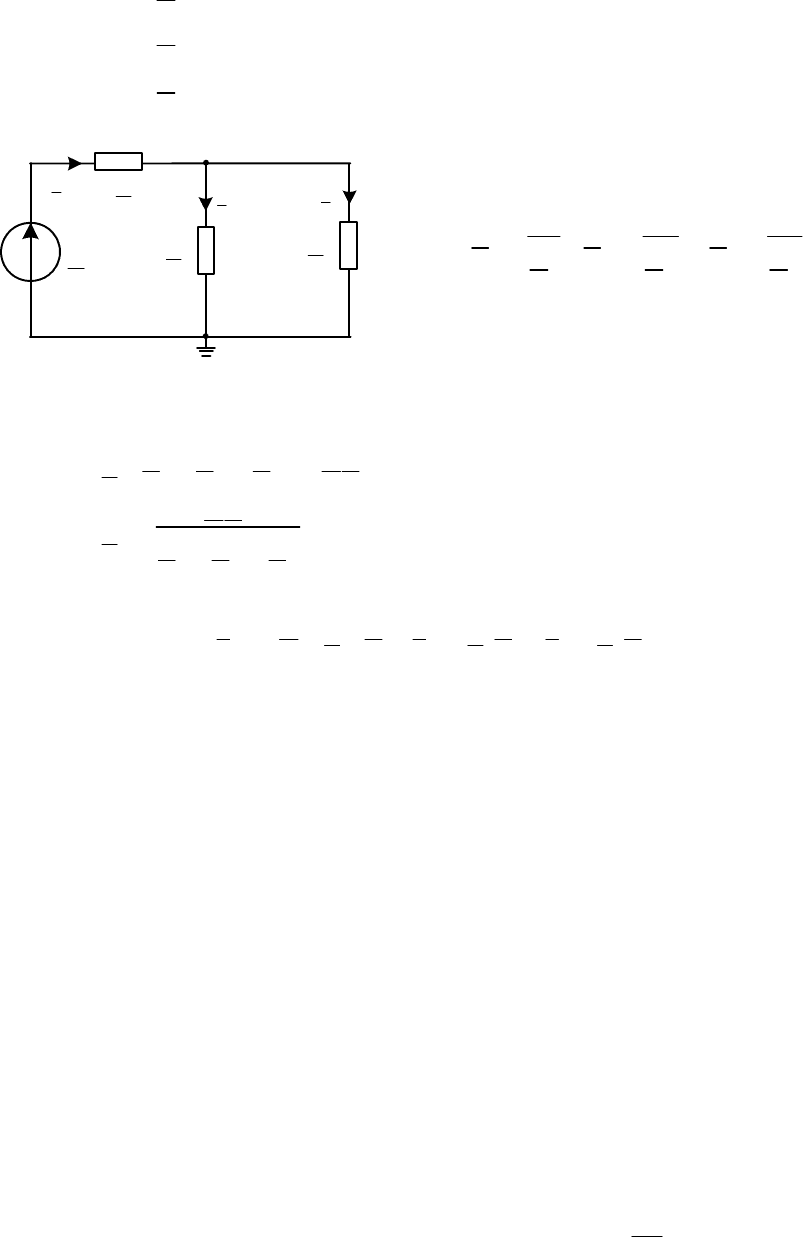
Рис. 2.24
64
1
1
2
2
3
20 31,416 Ом,
24094,248Ом,
20 25,488 Ом.
M
LM
LMC
ZRjX j
ZRjXX j
ZRjX X X j
Перерисуем схему замещения и запишем уравнения для потенциа-
лов методом узловых напряжений.
Находим проводимости ветвей
12 3
12 3
11 1
,, YY Y
Z
ZZ
,
а затем потенциал первого узла:
123 1
1
118,419
1
1
123
,
13,183 24,363 27,701 B.
j
YY Y EY
EY
je
YY Y
При известном потенциале можем определить токи во всех ветвях
112213
111
,,
I
EYI YIY
§2.9. Построение векторной диаграммы
Для построения векторной диаграммы в первую очередь нужно
задаться масштабом тока и напряжения. Следующим этапом строится
лучевая диаграмма токов, а затем по отношению к ней строится топо-
графическая диаграмма напряжений. Учитывая, что ток и напряжение
на активном сопротивлении находятся в фазе, векторы напряжения и
тока на диаграмме следует откладывать параллельно друг
другу, и на-
правленными в одну сторону. Напряжение на индуктивности опережает
ток индуктивности на 90 градусов, следовательно, вектор напряжения
откладывается перпендикулярно вектору тока с опережением (отклады-
вается против часовой стрелки). Напряжение на емкости отстает от тока
емкости на 90 градусов, следовательно, вектор напряжения откладыва-
ется перпендикулярно вектору тока с отставанием (откладывается по
часовой стрелке).
Приведем
пример построения диаграммы для нашей схемы. От-
кладываем в масштабе токи и напряжения
1
А/см, В/см
30
IU
MM
E
Z
1
I
2
I
1
I
3
Z
2
Z
3
1
2
Рис. 2.25

65
(см. диаграмму). Вычислим необходимые значения напряжений на эле-
ментах.
45
11
121
22
23
33
3
22
23
232
12
40 28, 28 28,28;
22,369 ;
17 ;
210,822;
26,861 ;
17,1 ;
45,36 ;
210,822;
26,861 ;
40,292 ;
8,5 .
j
R
LL
R
MM
R
CC
R
MM
LL
MM
Ee j
UIR B
UIX B
UIR B
UIX B
UIR B
UIX B
UIR B
UIX B
UIX B
UIX B
Определим показания вольтметра:
1
12 3
L
M
VIRIjX IjX или
2
2 28.28 28.28 0,169 0,211 40 29.27B VEIR j j
Рис. 2.27
Рис. 2.26

66
§2.10. Мощность в цепи переменного тока с взаимной индуктивно-
стью
Полная мощность, как и прежде, определяется выражением
*
22
1
,
N
kk
k
SEIPjQSPQ,
P – активная мощность, Q – реактивная мощность.
Потребляемая активная и реактивная мощности определяются соотно-
шениями соответственно:
11 1 2
222
,
111
2cos()
M
NNM
PRIQXI XI
L
C
kk kk kk
kkk
IIX .
Здесь токи
12
12
,
j
j
I
eIe ветвей, в которых находится индуктивности.
Знак плюс выбирается, когда в цепи согласное включение катушек. В
противном случае выбирается знак минус.
Ниже приводится электрическая схема, собранная в программно-
интегрированной среде Electronics Workbench с развязкой индуктивной
связи. При развязке индуктивной связи получается отрицательная ин-
дуктивность. В место отрицательной индуктивности можно поставить
эквивалентную емкость, которая
определяется выражением
2
1/
CM.
Приведем схему рассмотренной задачи собранную в среде Elec-
tronics Workbench.
Рис. 2.28
Ниже приводится программа вычисления в программно-
интегрированной среде MathCAD.

67
Магнитносвязанные катушки
Лекция № 7
§2.11. Трансформатор
Электрическая цепь состоит из контуров различного назначения.
Может оказаться, что для различных контуров цепи требуется отли-
чающиеся по величине напряжения. Для преобразования переменного
напряжения и для перераспределения энергии между контурами цепи,
широко применяется такое устройство как трансформатор.
Функциональные и конструктивные особенности трансформато-
ров весьма разнообразны. Мы
рассмотрим линейный трансформатор, в
котором отсутствуют нелинейные эффекты. Воздушные трансформато-
ры являются линейными.
Трансформатор состоит из двух или нескольких индуктивно свя-
занных катушек. Рассмотрим простой двухобмоточный трансформатор.
Двухобмоточный трансформатор состоит из двух обмоток – пер-
вичной и вторичной. К первичной обмотке подводится питание а ко
вторичной подсоединяется нагрузка–потребитель энергии. Токи и
на-
пряжения, относящиеся к первичной и вторичной обмоткам называют-
ся первичными и вторичными соответственно.
Рис. 2.29. Трансформатор
com I1()
1.118
0.509
62.921
0.996
com I2()
0.271
0.169
51.416
0.211
com I3()
0.855
0.34
66.539
0.784
SEI
1
S 42.567 13.766i PI1
2
R I2
2
R 2 I3
2
R
P 42.567
QI2
2
XL1 I3
2
XL2 Xc () Xm 2 I2 I3 cos arg I2( ) arg I3() () Q 13.766
i1 V I1 0.5 () i2 V I2 0.5 () i3 V I3 0.5()
i1 V I1 0.5()3
0
i2 V I2 0.5()3
0
i3 V I3 0.5()3
0
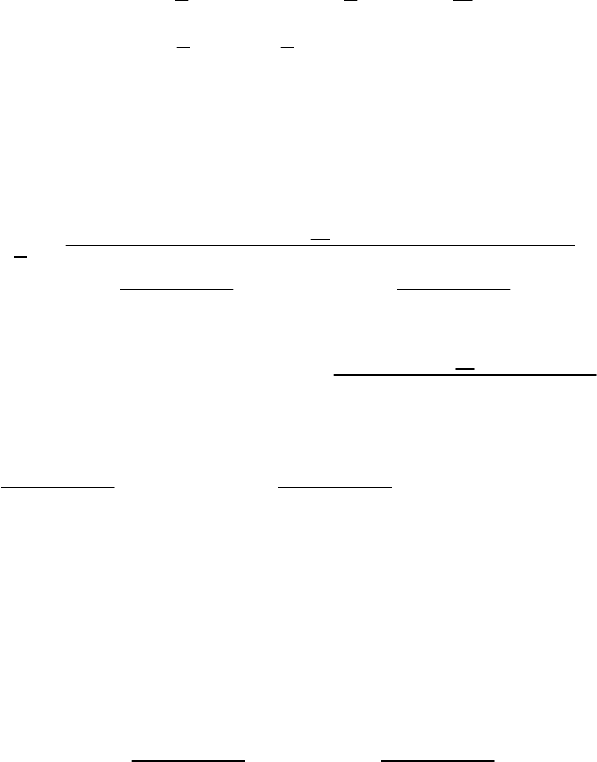
68
Для усиления магнитной связи используют ферромагнитные сер-
дечники вокруг, которых наматываются обмотки трансформатора (но
при этом трансформатор становится нелинейным).
Запишем второй закон Кирхгофа для трансформатора, введя обо-
значения элементов первичной и вторичной обмоток:
12222Н 22 2 Н
11
12
22 22
12
,, ;
;
0.
LL
M
M
XX R RRX X X
IR jX IjX E
IjX I R jX
(50)
Умножим первое уравнение на
22 22
R
jX , а второе уравнение на
M
j
X и затем сложим. В результате получим выражение тока первичной
обмотки через входное напряжение и сопротивления, вносимые вторич-
ной обмоткой
вн вн
,
R
X
:
1
22
22 22
11
22 22
22 22 22 22
1 вн 1 вн
,
MM
E
I
RX
RXjX X
RX RX
E
RR jX X
(51)
где
22
22 22
вн вн
22 22
22 22 22 22
,
M
M
RX
R
XX X
RX RX
.
Это выражение называется приведение сопротивлений вторичной
обмотки к сопротивлениям первичной обмотки. Из этого выражения
вытекает следующее. Для того, что бы трансформатор передавал мак-
симальную мощность во вторичную обмотку необходимо, чтобы вы-
полнялось соотношение:
22
22 22
11
22 22
22 22 22 22
,
M
M
RX
R
XX X
RX RX
. (52)
Построим качественно векторные диаграммы для трансформатора
при различных нагрузках:

69
а б
Рис. 2.30. Векторная диаграмма напряжений трансформатора при нагрузках:
а)
НН
Н
Z
RjX
и б)
НН
Н
Z
RjX
Что бы добиться выполнения соотношение (52) в первичную и во
вторичную цепи трансформатора включаются переменные емкости, что
позволяет варьировать реактивные составляющие сопротивлений пер-
вичной и вторичной цепях, рис. 2.31.
Рис. 2.31
Для приведенной схемы реактивные составляющие будут опреде-
лятся выражениями:
1122MН 2
1, 1
M
XX CX X X C.
Если разрешить первое выражение (52) относительно
22
X , то можно
получить:
22
22 1 22
22
1
M
XR RR
X
R
.
I
2
I
2
R
2
I
2
jX
L2
-I
1
jX
M
I
1
I
1
R
1
I
1
jX
L1
-I
2
jX
M
U
1
I
2
R
Н
I
2
jX
Н
I
2
I
2
R
2
I
2
jX
L2
-I
1
jX
M
I
1
I
1
R
1
I
1
jX
L1
-I
2
jX
M
U
1
I
2
R
Н
-I
2
jX
Н
70
Последнее выражение показывает, что при выполнении неравенства:
1222
122
M
R
R
XRR M .
Невозможно получить максимальную мощность во внесенном со-
противлении
вн
R
.
§2.12. Резонанс напряжений
L
e(t)
R
C
i(t)
Рис. 2.32
Рассмотрим схему, в которой последовательно соединены индук-
тивность емкость сопротивление и источник напряжения. Индуктивное
и емкостное сопротивления зависят от частоты
() , () 1
LC
XLX C. С увеличением частоты индуктивное со-
противление ()
L
XL увеличивается, и ток в цепи с индуктивностью
уменьшается. При уменьшении частоты емкостное сопротивление
уменьшается, и ток в цепи с емкостью увеличивается. Графическая за-
висимость индуктивного сопротивления
()
L
X от частоты приведена
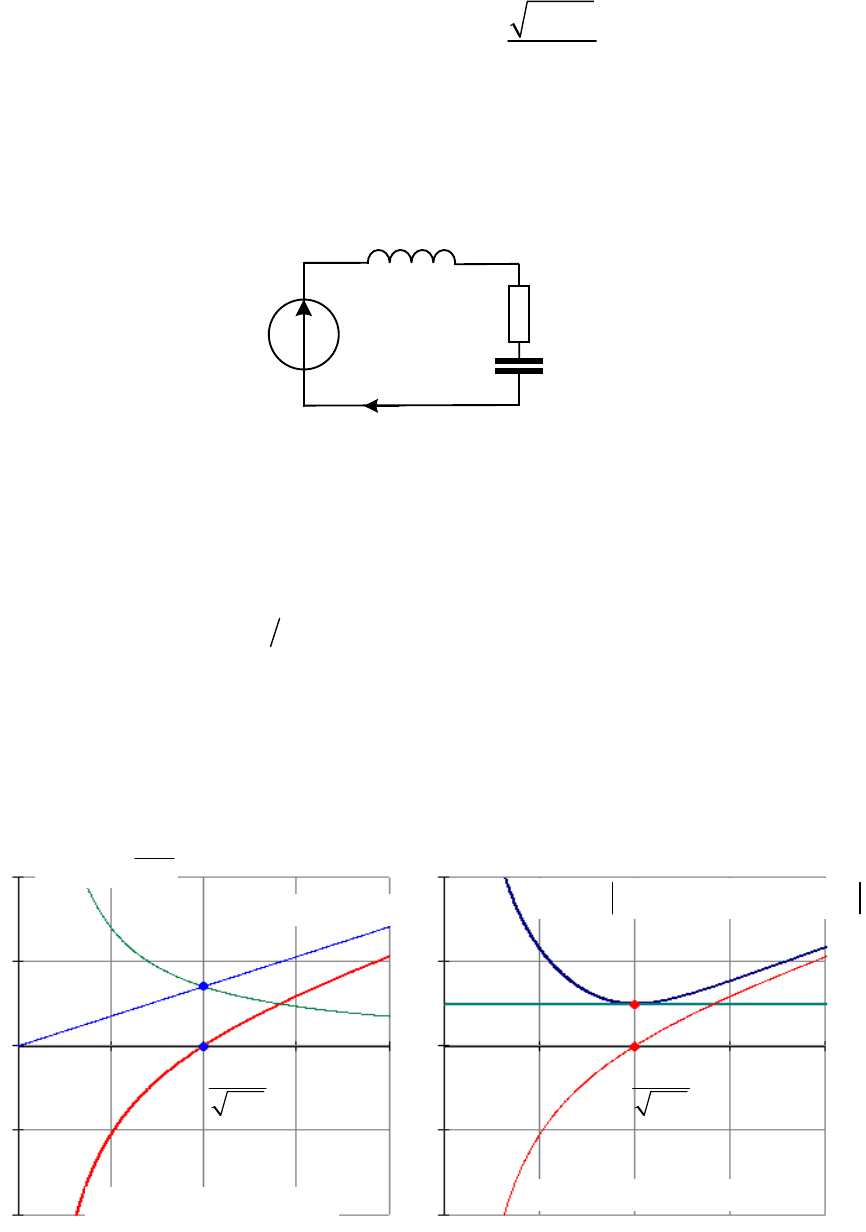
на рис. 2.33, она линейна.
1
()
C
X
C
()
L
XL
1
L
C
() () ()
LC
XX X
() () ()
LC
ZRjX X
1
L
C
() () ()
LC
XX X
R
Рис. 2.33
