Исаев Ю.Н., Колчанова В.А., Хохлова Т.Е., Васильева О.В. Курс лекций по теоретической электротехнике
Подождите немного. Документ загружается.

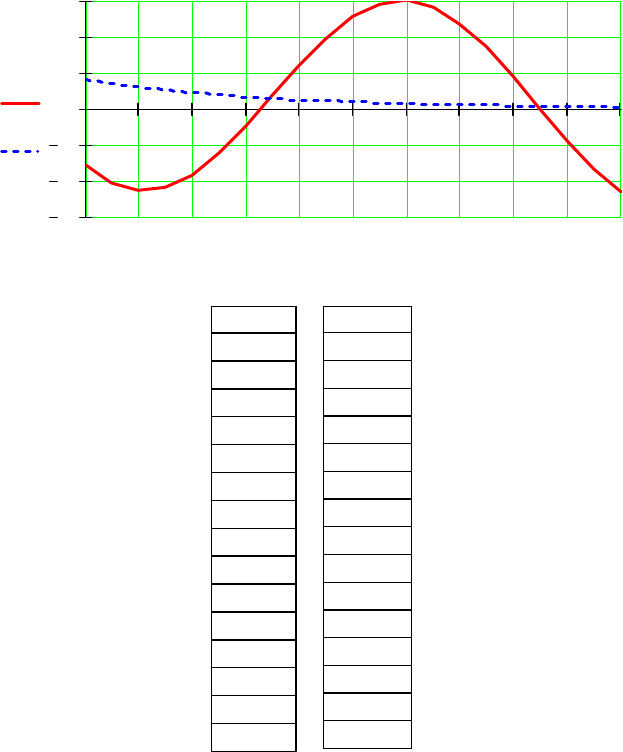
121
Рис. 4.36
0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018 0.02
0.3
0.2
0.1
0.1
0.2
0.3
it()
Ae
pt
t
t
0
0.001
0.002
0.003
0.004
0.005
0.006
0.007
0.008
0.009
0.01001
0.01101
0.01201
0.01301
0.01401
0.01501
it()
-0.156
-0.206
-0.227
-0.219
-0.183
-0.124
-0.049
0.036
0.12
0.196
0.255
0.291
0.3
0.282
0.237
0.171
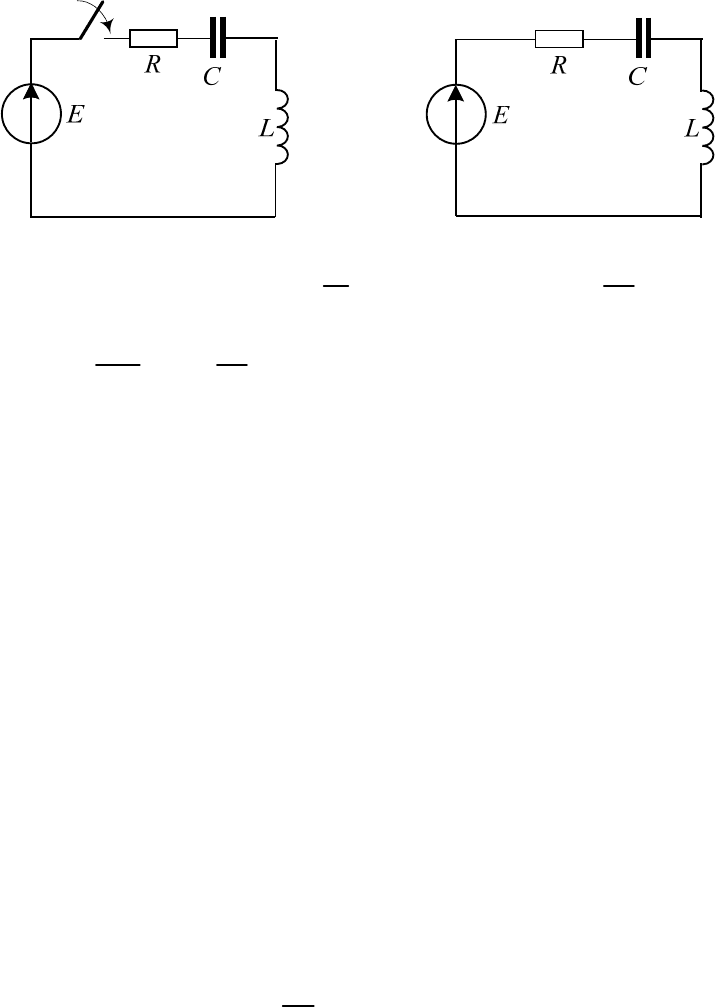
122
§4.4. Переходные процессы в цепи второго порядка
Рассмотрим цепь второго порядка представленную на рис. 4.37 с
параметрами:50B, 10Ом,0.1Гн,40мкФ.
E
RLС
Записываем уравнения по второму закону Кирхгофа, в результате
получаем систему дифференциальных уравнений:
Рис. 4.37
2
2
,;
.
LC C
di du
uuiRE L Riu EiC
dt dt
du du
LC RC u E
dt
dt
(1)
Решение данного уравнения будем искать в виде суммы двух со-
ставляющих:
112 2
( ) exp( ) exp( )
C св пр
ut u u A pt A pt E . (2)
Первое слагаемое это
112 2
exp( ) exp( )
св
uA ptA pt
свободная
составляющая. Она зависит только от параметров схемы, а также от на-
чальных и конечных запасов энергии. Эта составляющая решения не за-
висит от формы воздействующего напряжения.
Второе слагаемое это ()
пр C
uu
принуждённая составляющая.
Она зависит от внешнего воздействия и имеет форму этого воздействия.
Очевидно, что в нашем случае она определяется как ()
пр C
uu E
.
Постоянные интегрирования определяются из начальных условий,
отражающих невозможность мгновенного изменения начальных запасов
энергии в конденсаторе и в катушке.
Для определения констант интегрирования используем независи-
мые начальные условия
(0) 0, (0) 0
CL
ui
.
12
11 2 2
(0) 0 ;
(0) (0 ) 0 .
C
LC
uAAE
du
ii C CApAp
dt
(3)
Откуда следует, что
123
21
12
21 21
,
p
EpE
AA
p
ppp
. (4)
Теперь можно записать окончательное решение
12
21
12 21
21 21 21
( ) exp( ) exp( ) .
pt pt
C
pE pE E
ut pt pt E pe pe E
pp pp pp
Определим корни характеристического уравнения входящие в
решение ()
C
ut
12
,
p
p через входное сопротивление схемы.
2
2
11
010
CL p RC p
pL R CL p RC p
Cp Cp
. (5)
В результате решения уравнения получаются корни:
2
2
1,2
22
0
4
1
22 22
.
RC RC LC
bD R R
p
aCLLLLC
(6)
Где
2
R
L
– показатель затухания контура,
0
1
L
C
– угловая часто-
та незатухающих колебаний, при выполнении условия
22
0
имеем
2
22
0
1
2
св
R
jj j
LC L
.
Здесь
св
– частота свободных колебаний,
Корни уравнения определяются параметрами цепи и могут при-
нимать следующие возможные значения (рис. 4.38).
Дискриминант равен нулю. Кони вещественные, отрицательные и
кратные. Критический режим
1,2
2
R
p
L
() 1
t
C
ut E te E
.
Дискриминант положительный. Корни вещественные отрицатель-
ные и неравные. Апериодический режим
22
1,2 0
p
;
21
12
22
0
() e e
2
pt pt
C
E
ut p p E
.
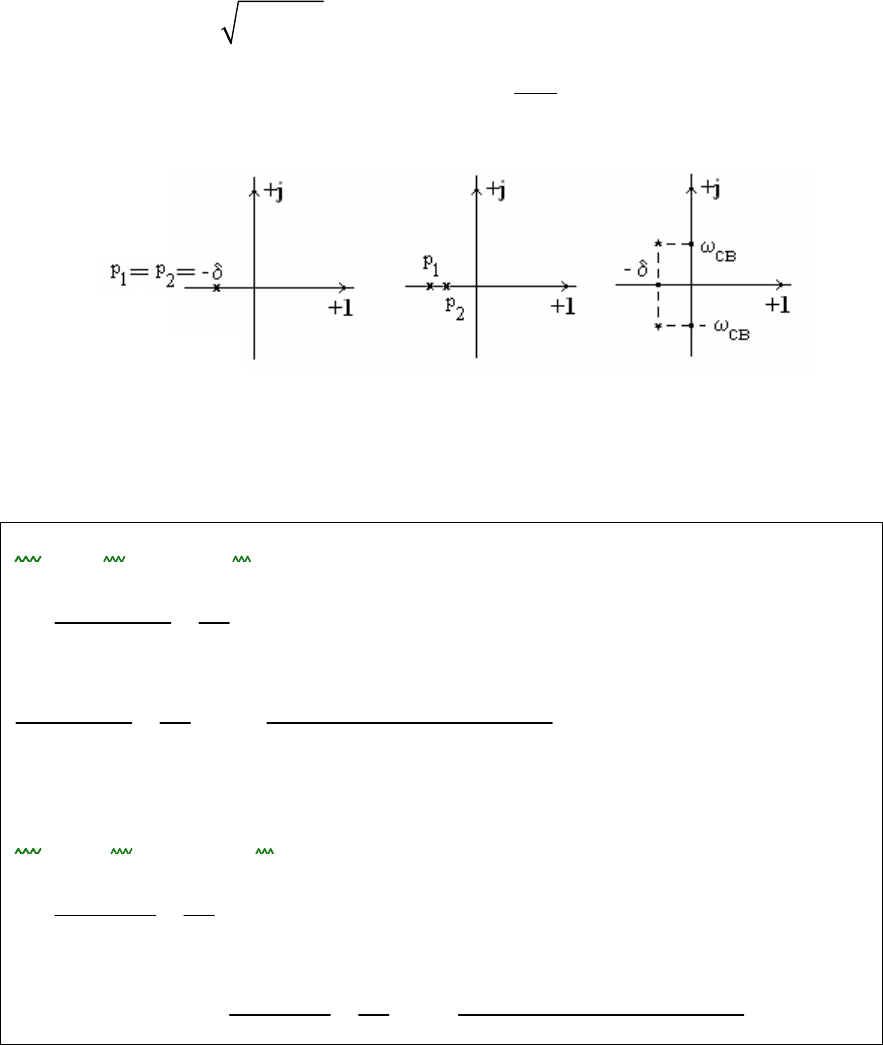
124
Дискриминант отрицательный. Корни комплексно-сопряжённые,
с отрицательной вещественной частью. Колебательный режим
22
1,2 0
св
p
jj .
() cos( ) sin( )
t
C св св
св
ut Ee t t E
.
Рис. 4.38. Расположение корней на комплексной плоскости.
Примеры определения корней характеристического уравнения в
MathCAD
R 10 C 60 10
6
L 0.
2
p
RLp
()2 R
RLp 2R
1
Cp
R solve p
456.2341361360570100
2
182.6547527528318788
6
RLp ()2 R
RLp 2R
1
Cp
R
5R
2
Cp 3RCp
2
L 3R Lp
3R Lp ()Cp
p
456.234
182.655
R 20 C 100 10
6
L 0.
1
P
RLP
()R
RLP R
1
CP
R solve P
275.( ) 156.12494995995995515i
275.
( ) 156.12494995995995515i
P
275
156.125i
275 156.125i
RLP ()R
RLP R
1
CP
R
3R
2
CP 2RCP
2
L 2R LP
2R LP ()CP
125
Примеры определения корней характеристического уравнения и
зависимых и независимых начальных условий
Пример: Определить независимые
(0), (0)
LC
iU
и зависимые на-
чальные условия
(0 ), (0 )
LC
Ui
. Определить корень характеристиче-
ского уравнения.
R
R
2R
R
R
R
R
E
L
C
J
E
ic(+0)
Uc(0)
iL(0)
Рис. 4.39 Рис. 4.40
Решение:
1. 1.Определяем независимые начальные условия
(0), (0)
LC
iU
.
1
(0) , (0) (0)
25 5
2
2
LCL
EE E
iUiR
R
R
R
.
2. Определяем зависимые начальные условия
(0 ), (0 )
LC
Ui
из схемы
после коммутации (см. документ Маthcad).
3. Определяем корень характеристического уравнения из схемы после
коммутации (см. документ Маthcad).
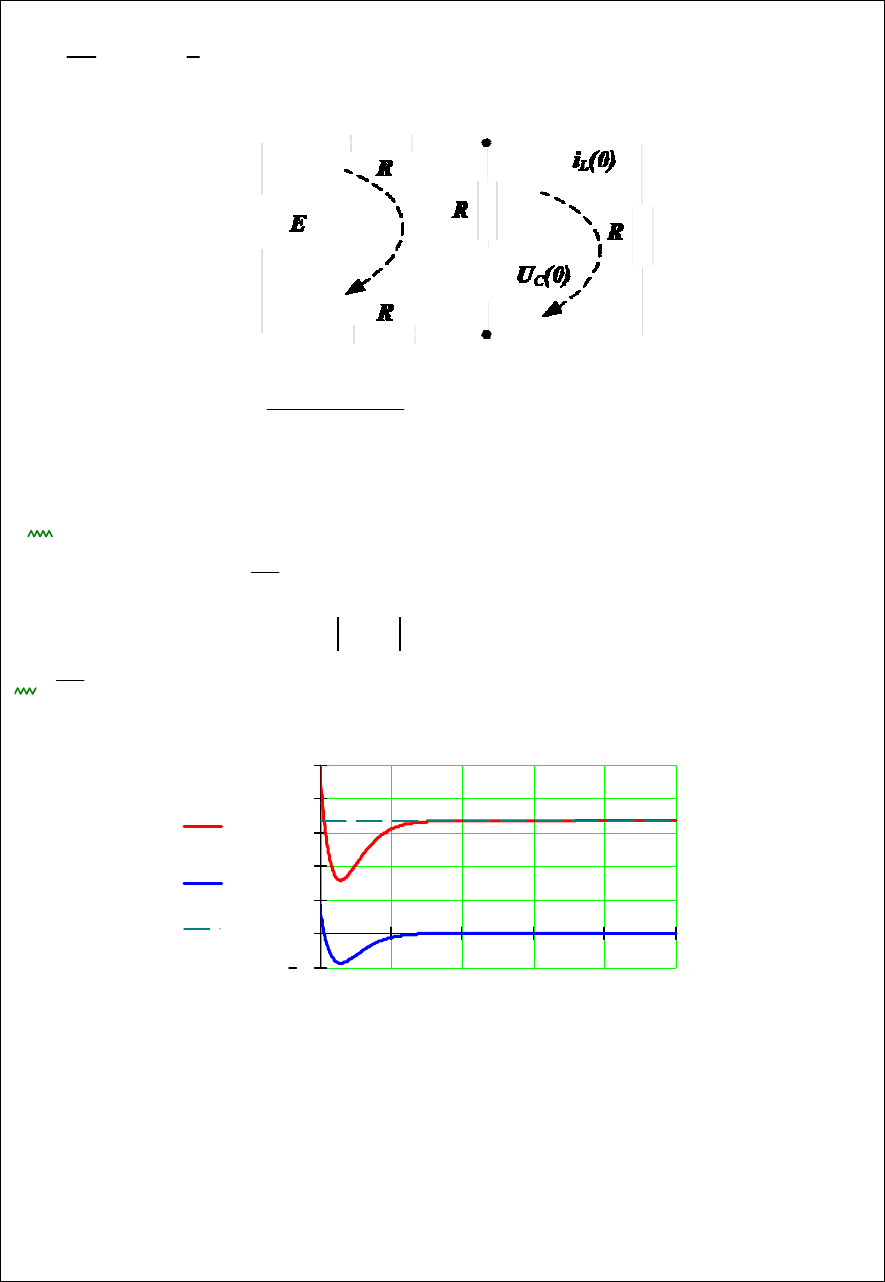
Документ MathCAD
Определить напряжение на конденсаторе.
Корни характеристического уравнения
ORIGIN 1
E 100 R
10 L 0.1 C 50 10
6
U
пр
E
3
Zp()
2R Lp R ()
3R Lp
R
1
Cp
pZp()
solve p
float 5
416.67 ( ) 162.45i
416.67 ( ) 162.45 i
p
416.67 162.45i
416.67 162.45i
126
Независимые начальные условия
Зависимые начальные условия
Рис. 4.42
Постоянные интегрирования
Рис. 4.43
i
Lo
E
2R
U
C0
E
2
i
Lo
5 U
C0
50 i
R0
EU
C0
i
Lo
R
3R
i
C0
i
R0
i
L
o
A
1
A
2
1
p
1
1
p
2
1
U
C0
U
пр
i
C0
C
A
1
A
2
8.333 81.221i
8.333 81.221i
Ut() 2Re A
1
e
p
1
t
U
п
р
Im p
1
162.45
U
пр
33.333
T
2
t 0 0.0001 0.0
5
0 0.01 0.02 0.03 0.04 0.05
10
10
20
30
40
50
Ut()
Re A
1
e
p
1
t
U
пр
t
127
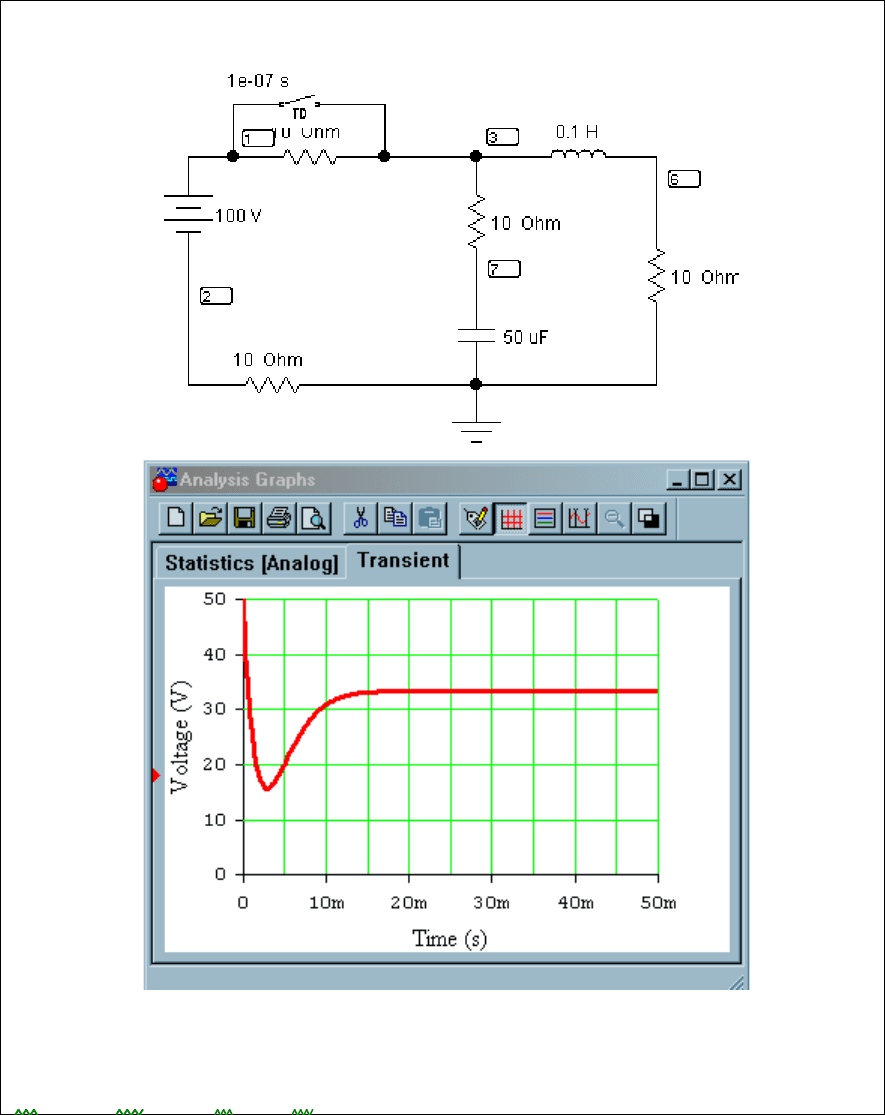
Проверка расчётов в среде EWB
Рис. 4.44
Определить ток индуктивности.
E 100 R 60 L 0.
1
C 50 10
6
128
Рис. 4.45
Рис. 4.46
Рис. 4.47
i
пр
E
R
i
пр
1.667 Z p()
RL p
RLp
R
1
Cp
pZp1()
solve p1
float 5
233.33 ( ) 213.44i
233.33 ( ) 213.44i
p
233.33 213.44i
233.33 213.44i
i
Lo
E
2R
U
C0
E
2
i
Lo
0.833 U
C0
50
i
R0
U
C0
i
Lo
R
2R
U
L0
Ei
R0
R
A
1
A
2
1
p
1
1
p
2
1
i
Lo
i
пр
U
L0
L
A
1
A
2
0.417 0.716i
0.417 0.716i
it() A
1
e
p
1
t
A
2
e
p
2
t
i
п
р
1
Re p()
3.031 10
3
t 0 0.01 1
0
0 0.0061 0.0121 0.0182 0.0242 0.0303
0.4
0.8
1.2
1.6
2
it()
i
пр
t
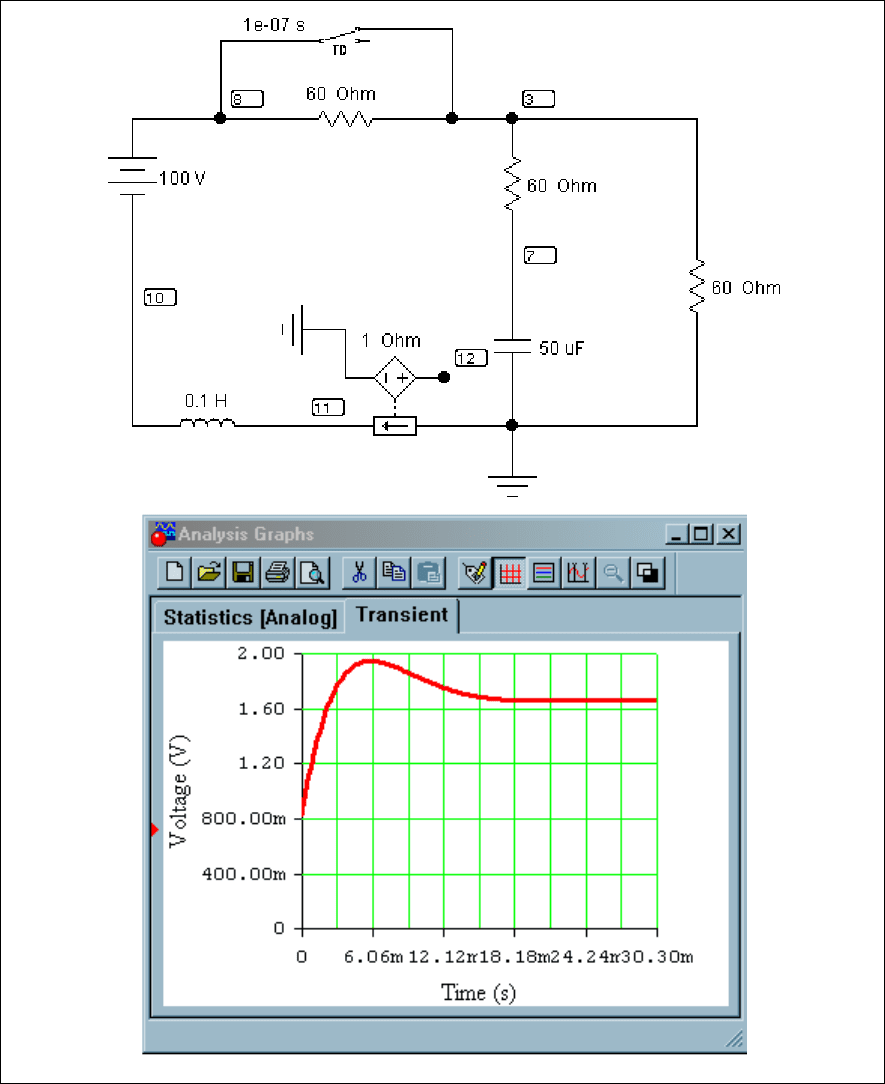
129
Рис. 4.48

130
§4.5. Операторный метод расчёта переходных процессов
Операторный метод (преобразование Лапласа) расчета переход-
ных процессов используется для того, чтобы обыкновенные дифферен-
циальные уравнения с постоянными коэффициентами (в пространстве
оригиналов) преобразовать в алгебраические (в пространстве изображе-
ний). Очевидно, что алгебраические уравнения решаются проще. После
решения алгебраического уравнения над полученной функцией (изо-
бражением) производится обратное преобразование Лапласа, получает-
ся оригинал
. Полученный оригинал – это функция, которая и будет ре-
шением дифференциального уравнения.
Любой функции можно сопоставить её преобразование Лапласа
0
() ()
pt
Fp fte dt
, (7)
здесь
()Fp
– изображение,
()
f
t
– оригинал. Выражение (7) записыва-
ют ещё и в операторной форме
() ()Fp Lft
.
Приведём изображение нескольких часто встречающихся функ-
ций.
Определим изображение константы – ( ) ( )
f
tAconst
:
0
0
()
pt
pt
eA
Fp Ae dt
p
p
.
Найдем изображение экспоненциальной функции – ( )
t
f
te
:
()
0
0
1
()
pt
tpt
e
Fp e e dt
pp
.
Изображение экспоненциальной функции поможет нам найти
изображения синусоидальной косинусной функций– sin( ), cos( )tt.
Для этого запишем эти функции через формулу Эйлера. Далее осущест-
вляем следующую цепочку преобразований:
22 22
22 22
11 1 1
sin( ) ;
22 2
11 1 1
cos( ) .
22 2
jt jt
jt jt
e e pj pj
t
jjpjpjjp p
ee pjpj p
t
pj pj p p
Определим изображение производной
()df t
dt
функции
()
f
t
, имеющей
изображение ()Fp
