Ипатов В.П. Широкополосные сигналы
Подождите немного. Документ загружается.

258
8.4. Слежение за кодом.
8.4.1. Оценка запаздывания в результате слежения.
В беспроводных приемниках, как правило, используется замкнутая петля слежения
в качестве инструмента непрерывного и точного измерения параметров. В зависимости от
характера измеряемого параметра ее примерами являются автоматическая регулировка
частоты, петля фазового слежения, автоматическая регулировка усиления и др. Строгое
математическое обоснование, доказывающее оптимальность петель слежения для изме-
няющихся во времени параметров сигнала, базируется на теории нелинейного оценивания
[88], однако их основная идея непосредственно следует из правила максимального прав-
доподобия (МП), рассмотренного в главе 2. Специфический характер приемника широко-
полосного сигнала проявляет себя главным образом в операции снятия расширения (см.
параграф 7.1), требующей точного синхронизма местной сужающей опоры с принятым
сигналом. Учитывая данный факт, сосредоточим основное внимание на точном измерении
задержки (фазы кода) принимаемого сигнала.
Для быстрейшего понимания упростим задачу, сведя ее к оцениванию задержки
модулирующего сигнала, не учитывая влияние случайности фазы. Предположим, что
является неизвестной задержкой модулирующего сигнала
)(ts
. Тогда в силу правила МП
(2.55) оптимальный измеритель должен формировать оценку
ˆ
этого параметра как его
значение, максимизирующее корреляцию
)(z
между опорной сигнальной копией
)( ts
и наблюдением
)(ty
. Одним из путей аппаратной реализации данного алгоритма служит
набор корреляторов (см. рис. 2.18), непосредственно вычисляющих функцию
)(z
в M
выборочных точках; другим является структура с согласованным фильтром, воспроизво-
дящая
)(z
в реальном времени (рис. 2.19, где детектор огибающей излишен для модули-
рующего сигнала). Однако обе эти схемы могут оказаться неосуществимыми в случае
применения широкополосного сигнала большой длины: первая из них вследствие множе-
ства корреляторов, а вторая – в связи со сложностью реализации согласованного фильтра
(см. пример 8.1.1).
Структура со следящей петлей представляет собой еще одну альтернативу. Отме-
тим, что в точке максимума
)(z
ее производная обнуляется:
0)()(
)(
)
ˆ
(
0
ˆ
T
dttsty
d
dz
z
. (8.20)
Назовем
)
ˆ
()
ˆ
(
ze
сигналом ошибки (error signal), причины для которого вскоре станут
ясны. Как видно, можно осуществлять поиск такого
ˆ
, который обратит сигнал ошибки в
нуль. Предположим, что истинная задержка сигнала равна
, предварительной оценкой
является
ˆ
и вычислим среднее сигнала ошибки по всем шумовым реализациям в
)(ty
:
TTT
dttstsdttstsdttstyze
000
)
ˆ
()()
ˆ
()()
ˆ
()()
ˆ
()
ˆ
(
. (8.21)
Последнее равенство следует после интегрирования по частям при учете, что интервал
интегрирования простирается на все «тело» сигнала вне зависимости от
:
0)()( Tss
. При аналогичных условиях среднее сигнала ошибки при
ˆ
(пред-
варительная оценка совпадает с истинным значением параметра) равняется нулю:
0
2
)]([
)()()
ˆ
(
0
2
0
T
T
ts
dttstse
,
однако в той же точке согласно последней части (8.21) производная от
)
ˆ
(e
259
T
dttsz
d
ed
0
2
ˆ
)]([)(
ˆ
)
ˆ
(
равна энергии производной сигнала со знаком минус, т.е. отрицательна. Последнее озна-
чает, что если
ˆ
лежит в достаточной близости слева от
, то
)
ˆ
(e
положительно, если же
ˆ
, то
)
ˆ
(e
отрицательно. Данное положение подсказывает структуру петли захвата по
задержки (delay-lock loop (DLL)), решающую соотношение (8.20) посредством ряда по-
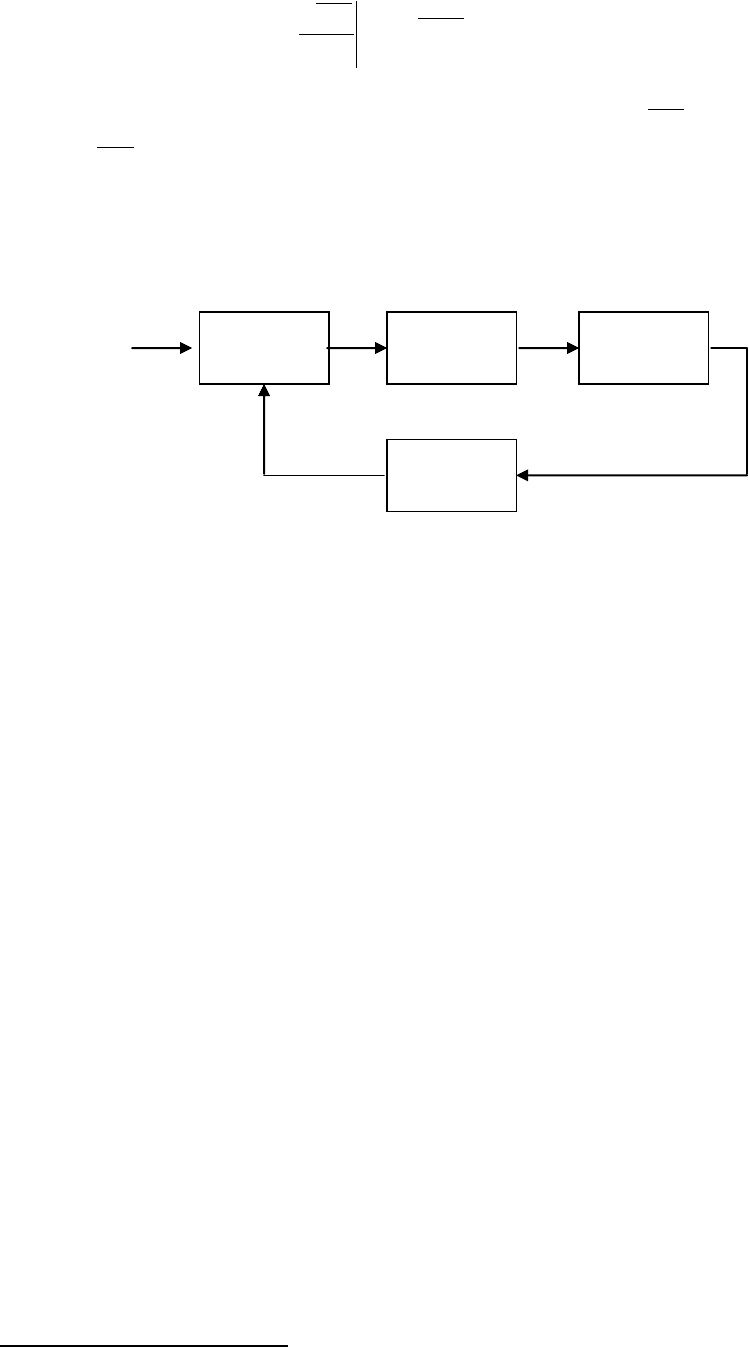
следовательных итераций и представленную на рис. 8.5. Местный генератор опоры фор-
мирует сдвинутую по времени копию производной сигнала
)
ˆ
(
ts
, которая используется
для вычисления корреляции с наблюдением
)(ty
. Затем результирующий сигнал ошибки
очищается от шумов посредством фильтра петли для приближения к среднему в (8.21).
Когда сглаженный сигнал ошибки положителен, то это с большой вероятностью свиде-
тельствует об опережении сигнала локальной опорой
)
ˆ
(
ts
и вынуждает генератор
управляемый напряжением (ГУН) (voltage controlled oscillator (VCO)) снизить свою часто-
ту, т.е. увеличить задержку (оценочную) опоры
ˆ
. В противном случае сглаженный отри-
цательный сигнал ошибки приводит ГУН
1
к необходимости увеличения частоты, т.е.
уменьшает задержку опоры. Очевидно, что в устойчивом состоянии DLL удерживает сиг-
нал ошибки в районе нуля, обеспечивая синхронизм между локальной опорой и принятым
сигналом.
Очевидно, что для адекватной работы DLL нуждается в начальном целеуказании,
т.е. стартовом значении
ˆ
, которое достаточно близко к истинной задержке сигнала. С
одной стороны, данное условие накладывает определенные требования к точности проце-
дуры поиска. С другой стороны, опорное колебание, получаемое на основе МП правила,
обычно не осуществимо (например, оно может содержать дельта–функции, если сигнал
состоит из прямоугольных чипов). Как правило, оно заменяется некоторым другим сигна-
лом, который, будучи более подходящим для практической реализации, сохраняет основ-
ные свойства: отчетливую нечетную зависимость сигнала ошибки на выходе коррелятора
от ошибки оценивания
ˆ
. При конструировании подобной опоры решающую роль мо-
жет играть желание обеспечить втягивание (достижение синхронизма) при более мягких
требованиях к начальному целеуказанию. Более подробно это будет рассмотрено в 8.4.3.
8.4.2. Ранне–поздние дискриминаторы DLL.
Первым элементом в структуре DLL является дискриминатор, т.е. комбинация из
1
В реальном исполнении входная величина, управляющая частотой генератора, необязательно является на-
пряжением, например, в цифровой реализации петли входное число играет аналогичную роль. Однако, для
избежания излишней множественности терминов будем использовать название ГУН в качестве универсаль-
ного.
Коррелятор
Фильтр
петли
ГУН
Рис. 8.5. Обобщенная структура DLL.
)(ty
)
ˆ
(
ts
Опорный
генератор
)
ˆ
(e
260
коррелятора и опоры, формирующая сигнал ошибки
)
ˆ
(e
. В одной из классических схем
дискриминатора DLL для модулирующего сигнала
)(ts
в качестве опоры
)(ts
r
берется
разность двух сдвинутых по времени копий сигнала: запаздывающей
)2/( ts
и опере-
жающей
)2/( ts
, где
определяет их временное разнесение. Тогда полезный компо-
нент сигнала ошибки, обусловленный рассогласованием
ˆ
опоры и принятого сиг-
нала, может быть записан в виде
TT
r
dttststsAdttstsAe
00
2
ˆ
2
ˆ
)()
ˆ
()()
ˆ
(
)]2/()2/([ AE
, (8.22)
где E – энергия стандартного сигнала
)(ts
за время интегрирования T, A – амплитуда при-
нятого сигнала, взвешенная относительно
)(ts
, а
)(
– нормированная АКФ сигнала, вы-
численная на временном интервале
],0[ T
. Возьмем, например, периодический дискретный
сигнал (широкополосный код) длины N с длительностью чипов
, и пусть время интегри-
рования простирается на целое число l периодов сигнала:
lNT
, тогда
)(
– периоди-
ческая АКФ. Если
)(ts
является минимаксной бинарной последовательностью (m–
последовательностью, последовательностью Лежандра и т.п.) с прямоугольными чипами,
то ее нормированная периодическая АКФ
)(
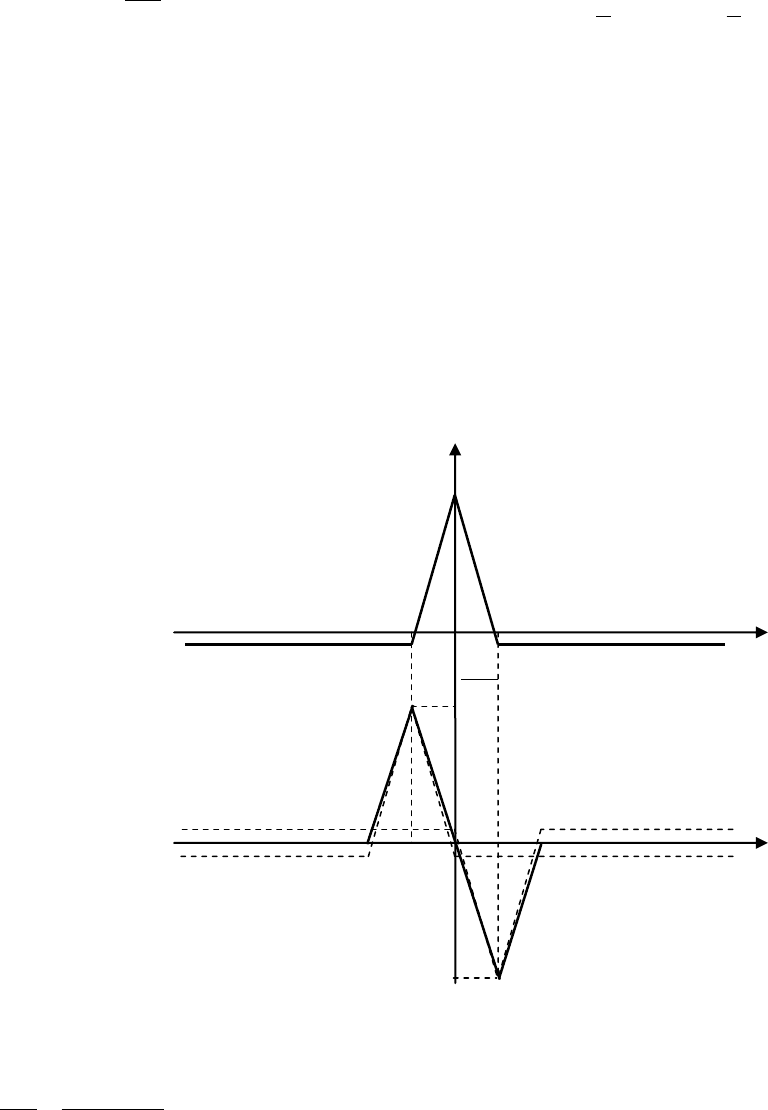
имеет вид, представленный на рис. 8.6, a.
Опережающая и запаздавающая копии
)(
, входящие в соотношение (8.22), показаны на
рис. 8.6, b пунктирными линиями для примерного разнесения
2
, а их разность
)
ˆ
()( ee
, называемая дискриминационной кривой, также представлена на этом ри-
сунке сплошной линией. Легко заметить, что рассматриваемый дискриминатор полностью
отвечает выдвинутым требованиям: опережающая и запаздывающая опорные версии
входного сигнала соответственно порождают положительный или отрицательный сигнал
1
)(
0
a)
b)
Рис.8.6. Дискриминационная кривая ранне-поздней DLL.
1
1
)(e

261
ошибки, предоставляя возможность ГУНу изменить собственную частоту и, тем самым,
сдвинуть опору в соответствующем направлении.
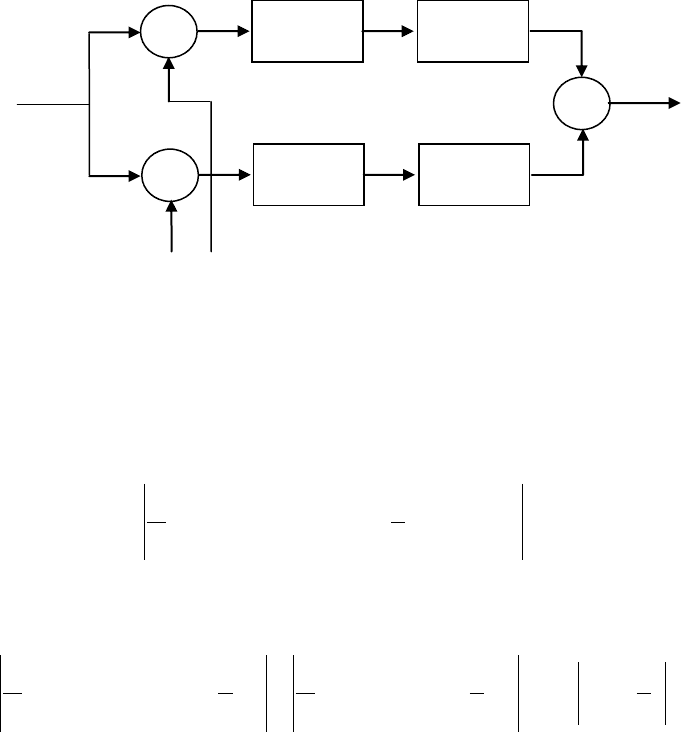
На рис. 8.7 представлена одна из возможных структур ранне–позднего дискрими-
натора для модулирующего сигнала. Кодовый генератор, управляемый ГУНом, формиру-
ет опережающую сигнальную копию
)2/( ts
, которая, задержанная на
, дает запазды-
вающую копию. Их разность подается на коррелятор в качестве опорного сигнала. Кодо-
вая копия
)(ts
, синхронизированная с входным сигналом и используемая для снятия рас-
ширения спектра, может быть получена в результате задержки на
2/
опережающей ко-
пии. Если кодовый генератор построен на основе регистра сдвига и
2
, то отсутствует
необходимость во введении дополнительных элементов задержки, поскольку все три ко-
пии могут быть считаны с трех последовательных разрядов регистра.
Альтернативная схема такого же дискриминатора включает два коррелятора, кото-
рые первоначально раздельно вычисляют корреляции наблюдения с опережающей и за-
паздывающей копиями сигнала, а затем осуществляется вычитание полученных результа-
тов с целью получения сигнала ошибки
)
ˆ
(e
[18, 77].
В случае полосного сигнала рассмотренный дискриминатор может быть применен,
если петля восстановления фазы приемника предварительно синхронизирована с несущей
частотой принимаемого сигнала, так что полосный сигнал может быть трансформирован в
его действительный низкочастотный эквивалент. По этой причине данный дискриминатор
часто называют когерентным, также как и содержащую его схему DLL. Если предвари-
тельная фазовая синхронизация не возможна, то используется некогерентный дискрими-
натор, основанный на сравнении квадратов модулей двух корреляций. Они вычисляются
между наблюдаемой комплексной огибающей
)(tY
и комплексными огибающими двух
опор, формируемых в виде опережающей и запаздывающей копий кода сигнала. Прежде
всего, данный дискриминатор оказывается эффективным несмотря на наличие модуляции
данными. На практике он часто реализуется структурой, изображенной на рис. 8.8, где
умножение комплексных огибающих осуществляется посредством гетеродинирования
(см. комментарии в конце параграфа 7.1.2). Рассмотрим работу данной структуры, игно-
рируя входной шум и, не нарушая общности, полагая
0
. Пусть опоры представляют
собой сдвинутые во времени копии расширяющего сигнала, обладающего комплексной
огибающей
)(tS
и несущей частотой
1
f
, которая отличается от несущей принятого сигна-
ла
0
f
:
jtfjtSts
r 1
2exp
2
Re
2
,
Коррелятор
От ГУН
Рис.8.7. Ранне–поздний дискриминатор модулирующего сигнала
)(ty
)2/
ˆ
( ts
Кодовый
генератор
)
ˆ
(e
2/
2/
+
)2/
ˆ
( ts
)
ˆ
( ts
r
К фильтру
На сужение
)
ˆ
( ts
262
где начальная фаза
в окончательном результате не будет играть никакой роли. Ком-
плексная огибающая приходящего сигнала
)exp()()( jtStBA
включает в себя наряду с
расширяющим кодом также амплитуду сигнала A, компонент
)(tB
модуляции данными и
неизвестную начальную фазу
. После умножения входного сигнала на опорные колеба-
ния и выделения низкочастотного компонента два результирующих полосных сигнала
разностной несущей частоты
10
ff
будут обладать комплексными огибающими вида
)](exp[)2/()()(
*
jtStStBA
. Предположим, что полосные фильтры после умно-
жителей обладают импульсной характеристикой с комплексной огибающей
)(tH
. Тогда
вещественные огибающие на выходах фильтров, вычисленные в терминах интеграла
свертки (см. параграф 2.12.1), имеют вид
dtHSSB
A
)(
2
)()(
2
*
.
Если импульсная характеристика фильтра представляет собой прямоугольник длительно-
сти T, равной длительности символа данных, а модуляция данных – фазовая, тогда выбор-
ки выходной вещественной огибающей в моменты
Tt
22
)(
22
)()(
2
0
*
0
*
AEdttStS
A
dttStStB
A
TT
,
пропорциональны модулю соответствующего значения АКФ
)(
расширяющей ком-
плексной огибающей. Разность квадратов модулей снова дает дискриминационную кри-
вую формы, подобную изображенной на рис. 8.6 (см. задачи 8.7, 8.15).
Реализация схемы на рис. 8.8 может столкнуться с трудностями, обусловленными
дисбалансом параметров опережающей и запаздывающей ветвей. Известны различные
решения по их преодолению [9,18,77], включая петлю с
–джиттером (tau-dither loop)
(другое название – с временным разделением – «time-shared»), где используется только
одна ветвь, переключающаяся поочередно между опережающим и запаздывающим образ-
цами.
8.4.3. Шумовые характеристики петли захвата по задержке (DLL).
Петля с захватом по задержке (DLL) является частным случаем схемы фазовой ав-
топодстройки (phase-lock loop) и проявляет такие же трудности в части анализа своего по-
ведения, которые присущи нелинейным системам с обратной связью [89,90]. Однако одна
из наиболее важных характеристик работы DLL – шумовая ошибка устойчивого состоя-
ния устройства слежения за задержкой – легко вычисляется при условии применимости
Рис.8.8. Ранне–поздний некогерентный дискриминатор
)(ty
)2/
ˆ
( ts
r
+
Полосный
фильтр
Квадратич.
детектор
Полосный
фильтр
Квадратич.
детектор
)2/
ˆ
( ts
r
К петлевому
фильтру
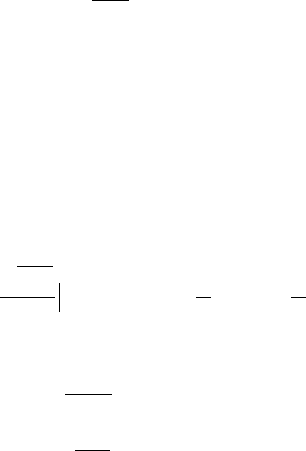
263
линейной аппроксимации.
В реальной практике, как правило, желательна достаточно малая шумовая ошибка,
свидетельствующая о хорошей способности петли к фильтрации шума. Флюктуации вы-
ходного сигнала петли могут считаться малыми, если ошибка, т.е. разность между истин-
ным текущим значением задержки сигнала
и ее оценкой
ˆ
, вырабатываемой DLL,
удерживается в рамках линейной зоны дискриминационной кривой с вероятностью, близ-
кой к единице. Если это условие выполняется, то можно полагать, что дискриминацион-
ная кривая линейна в широком диапазоне значений ошибки
ˆ
. Последнее позволяет
линеаризовать модель системы следующим образом.
Ограничимся узкополосным (или, что эквивалентно, когерентным) дискриминато-
ром DLL и вычислим спектральную плотность мощности шума
)(
~
fN
d
на его выходе.
Поскольку коррелятор подобного дискриминатора вычисляет корреляцию наблюдения с
опорным сигналом
)2/()2/()( tststs
r
, то, согласно (2.15), выходная дисперсия
шума определяется как
2/
0
2
r
EN
, где
r
E
– энергия опорного сигнала за время интег-
рирования T. Если, как и ранее, E – энергии стандартного сигнала, то
)](1[2 EE
r
и
)](1[
0
2
EN
. Интегрирование на интервале T может трактоваться как низкочастот-
ная фильтрация с полосой
TW
f
/1
, означающая, что найденная мощность шума распре-
делена в данной полосе и, следовательно, односторонняя спектральная плотность мощно-
сти шума на выходе дискриминатора составит
)](1[)(
~
0
2
ETN
W
fN
f
d
. (8.23)
При прямоугольной форме чипа и пренебрежимо малом уровне боковых лепестков
)(
представляет собой треугольник с единичной высотой и основанием , так что
ETNfN
d 0
)(
~
при
.
Замена истинной дискриминационной кривой ее воображаемой линейной аппрок-
симацией просто означает бесконечное продолжение линейного участка в окрестностях
нуля с тем же наклоном
d
S
. Последняя величина может быть найдена из (8.22), учитывая
четность АКФ
22
)(
0
AE
d
ed
S
d
.
Повторное обращение к треугольной форме АКФ дает
,2,
,2,2
2
AEW
AE
AEW
AE
S
d
(8.24)
где подставлена оценка полосы дискретного сигнала
/1W
.
Представим теперь, что вместо истинного шума
)(tn
, который добавляется к при-
нятому сигналу, непосредственно к измеряемому параметру
прибавляется эквивалент-
ный шум
)(tn
со спектральной плотностью мощности
2
/)(
~
)(
~
dd
SfNfN
. На выходе
линейного дискриминатора, заменяющего реальный аналог, этот воображаемый шум бу-
дет не отличим от истинного шума на выходе реального дискриминатора, поскольку его
спектральная мощность
)(
~~
2
fNNS
dd
является абсолютно такой же. В итоге приходим к
модели системы, изображенной на рис. 8.9, на вход которой поступает не сигнал, иска-
женный шумом, а параметр
в смеси с воображаемым аддитивным шумом
)(tn
. Данная
смесь обрабатывается линейной замкнутой петлей, в которой оценка
ˆ
вычитается из

264
входной величины, образуя выходной сигнал ошибки
. Затем фильтр с передаточной
функцией
)(
~
fh
сглаживает сигнал ошибки
, умноженный на крутизну дискриминатора
d
S
, вырабатывая выходную оценку
ˆ
. В данном варианте фильтрация включает в себя
операции, выполняемые петлевым фильтром и ГУНом по превращению сигнала ошибки
реального дискриминатора
)(te
в соответствующий сдвиг опорного сигнала. Данная мо-
дель является полностью линейной, и дисперсия
}{D
случайных флюктуаций на ее вы-
ходе может быть найдена на основе принципа суперпозиции не зависимо от сигнального
компонента как
0
2
)(
~
)(
~
}
ˆ
{ dffhfND
l
, (8.25)
где
)(
~
fh
l
– передаточная функция замкнутой петли. Для нахождения последней характе-
ристики достаточно подать на вход петли дельта–функцию. Тогда выходной спектр, яв-
ляющийся в точности
)(
~
fh
l
, подчиняется соотношению
)(
~
)](
~
1[)(
~
fhSfhfh
dll
, приво-
дящему к правилу, которое хорошо известно из теории линейных систем с обратной свя-
зью [2,7]
)(
~
1
)(
~
)(
~
fhS
fhS
fh
d
d
l
. (8.26)
Эквивалентный спектр флюктуаций задержки
)( fN
распределен в полосе
TW
f
/1
, ко-
торая, как правило, значительно шире полосы замкнутой петли; в противном случае по-
следняя не сможет эффективно сгладить флюктуации шума. Это допускает следующую
версию (8.25)
2
)(
~
)(
~
}
ˆ
{
d
Nd
N
S
BfN
BfND
, (8.27)
в которой шумовая полоса петли
N
B
определяется как
0
2
0
2
)(
~
1
)(
~
)(
~
df
fhS
fhS
dffhB
d
d
lN
.
Теперь, возвращаясь к (8.23) и (8.24) и отмечая, что
0,/1)(
, можно пред-
ставить (8.27) в следующей форме
)(tn
+
ˆ
Фильтр
)(
~
fh
d
S
Рис.8.9. Линеаризованная модель DLL.
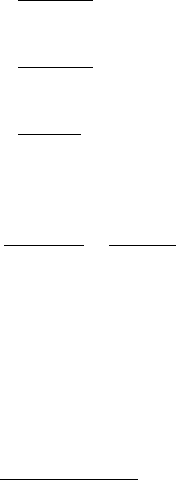
265
,2,
1
,2,
4
1
,0,
4
/
}
ˆ
{
22
22
22
l
l
l
qW
qW
qW
D
(8.28)
где
NN
l
BN
PA
TBN
EA
q
0
2
0
2
2
, (8.29)
называется отношением сигнал-шум в петле. Причина для такого названия очевидна: чис-
литель (8.29) содержит действительную энергию сигнала, поскольку
TEP /
– мощность
стандартного (имеющего амплитуду A=1) сигнала. В то же время знаменатель представля-
ет собой мощность шума в пределах шумовой полосы петли.
Соотношение (8.28) полностью подобно формуле Вудворда для потенциально дос-
тижимой точности временного измерения, представленной в параграфе 2.12.2:
1,
)2(
1
}
ˆ
{
22
q
qW
D
rms
,
подчеркивающее, что следящая петля является адекватным способом временного измере-
ния.
Имеются три параметра, затрагивающие точность DLL в устойчивом состоянии:
уровень сигнала относительно шума
0
2
/ NPA
, шумовая полоса петли
N
B
и расстояние
между опережающим и запаздывающим стробами. Первый из них представляет собой
«грубый» ресурс повышения точности и не нуждается в специальных пояснениях. Опти-
мизация по второму параметру не является простой задачей, поскольку механическое
уменьшение шумовой полосы без тщательного проектирования петлевого фильтра может
драматически ухудшить такие динамические свойства системы, как длительность захвата
и способность отслеживания сигнала с изменяющимся временем задержки. Выбор разне-
сения
также является предметом компромисса: уменьшение
по сравнению с длитель-
ностью чипа
обеспечивает более высокую точность оценки благодаря положительной
корреляции шума на выходе опережающей и запаздывающей ветвях. В то же время, чем
меньше разнесение
, тем уже сама дискриминационная характеристика (см. рис. 8.6).
Это предполагает более жесткие требования к точности поиска, поскольку последний
должен гарантировать попадание временного рассогласования между локальной опорой и
принятым сигналом внутрь активной (не нулевой) зоны дискриминационной характери-
стики. Другим фактором, которым нельзя пренебрегать, является опасность потери син-
хронизма, увеличивающаяся при сужении дискриминационной характеристики. Обще-
принятым путем достижения согласия между конфликтующими требованиями к парамет-
рам следящей петли служит процедура адаптации: на начальном этапе ввода в слежение
могут использоваться более широкая шумовая полоса и большее разнесение, которые по-
сле окончания переходных процессов уменьшаются для достижения более высокой точ-
ности в устойчивом состоянии.
266
Задачи.
8.1. Необходимо организовать последовательный поиск с постоянным временем
анализа
2
d
t
мс. Дискретный сигнал, который необходимо отыскать, занимает полосу
1 МГц и обладает кодом длиной L=1000. Отсутствует априорная информация о фазе кода,
а начальное частотное рассогласование местного генератора и несущей частотой сигнала
лежит в диапазоне
10
КГц. Грубо оценить минимальное число анализируемых ячеек.
8.2. Найти асимптотические приближения полной средней вероятности и среднего
числа шагов последовательного поиска, если вероятность ложной тревоги очень мала
)1(
f
Mp
. Дать практическое толкование полученным результатам.
8.3. Используется последовательный поиск с фиксированным временем анализа и
порогом, оптимизированным для некоторой мощности сигнала P. Что произойдет с пол-
ной средней вероятностью поиска и средним числом шагов в двух предельных случаях:
0P
и
P
, если не производить перенастройку времени анализа и порога? Дать
обоснование полученных результатов.
8.4. Найти выражения для вероятностей ложной тревоги и обнаружения, а затем
для времени анализа на ячейку, необходимого для обеспечения заданных
df
pp ,
, если
флюктуации амплитуды сигнала подчиняются закону Релея (3.12), а случайная начальная
фаза равномерно распределена на интервале
],[
. (Подсказка: простейшим путем явля-
ется трактование сигнала в качестве гауссовского процесса, независимого от шума.)
8.5. Найти выражение для вероятности правильного завершения и времени поиска
для последовательности быстрого поиска Стиффлера периода
n
L 2
.
8.6. Построить дискриминационную кривую когерентной DLL для случаев
0,
и
2
. Определить протяженность зоны максимальной крутизны.
Почему значения
2
неуместны?
8.7. Построить дискриминационную кривую некогерентной схемы DLL при разне-
сении
. Почему значение
2
неуместно?
8.8. Показать, что генератор, управляемый напряжением, схемы DLL функциони-
рует, как интегратор сигнала ошибки. Предполагается отсутствие шума на входе и посто-
янство задержки сигнала. Доказать, что в установившемся режиме ошибка на выходе DLL
равна нулю. Будет ли данное утверждение верно, если задержка сигнала линейно изменя-
ется, а DLL не содержит дополнительных интеграторов?
8.9. Рассмотрим схему DLL без дополнительного петлевого фильтра. Предполага-
ется, что кривизна дискриминатора равна 0.5 В/мкс, а ГУН изменяет свою частоту на
100 КГц на 1 В. Первоначальная разность частот ГУНа и принятого сигнала составляет
10 КГц. Определить величину ошибки в установившемся состоянии DLL при отсутствии
шума.
8.10. Определить шумовую полосу и дисперсию выходной ошибки в терминах кру-
тизны дискриминатора и усиления ГУНа схемы DLL, не содержащей петлевой фильтр.
Дать обоснование зависимости этих характеристик от параметров системы.
267
9. Канальное кодирование в широкополосных системах.
9.1. Предварительные замечания и терминология.
В ходе передачи, хранения и обработки данные необходимо представлять в некото-
рой подходящей форме. В цифровой связи первичное сообщение, вырабатываемое источ-
ником, может рассматриваться, как последовательность бит данных или битовый поток
(bitstream). Битовый поток отображается в последовательность символов некоторого оп-
ределенного алфавита, что традиционно называется кодированием. Цели кодирования мо-
гут быть различными. Например, термины кодирования источника или компрессии дан-
ных означает ликвидацию избыточности битового потока с целью представления данных
источника в наиболее экономичной форме. Другим вариантом кодирования является
шифрование, осуществляемое для защиты данных от непреднамеренного перехвата или
фальсификации. Предметом данной главы является канальное кодирование, направленное
на обеспечение передачи данных по каналу связи, максимально невосприимчивой к вред-
ным эффектам неустраняемых канальных помех. Частные ситуации, рассмотренные в па-
раграфах 2.3, 2.5–2.7, показывают насколько важно найти соответствующий сигнальный
вариант для преодоления разрушительного влияния канального шума. Наряду модуляцией
канальное кодирование предоставляет инструментарий для эффективной сигнализации.
В течение более чем пятидесятилетнего существования теория канального кодиро-
вания руководствовалась и мотивировалась фундаментальной теоремой Шеннона о про-
пускной способности канала, упомянутой в главе 1. Согласной этой теореме, любой канал
характеризуется некоторой константой C (выраженной в бит/сек), называемой пропускной
способностью, которая определяет верхнюю границу достижимой скорости R передачи
информации по каналу. Если
CR
, то не существует способа построения сигнала, обес-
печивающего произвольную достоверность передачи данных. Наоборот, когда
CR
все-
гда можно найти код, гарантирующий любую желаемую вероятность перепутывания од-
ного сообщения с другим на приемной стороне (см. рис 1.1). Теорема о пропускной спо-
собности Шеннона, давая строго математическое обоснование существования кода, не
указывает никакого конкретного кодового алгоритма достижения устанавливаемого ею
качества. Более того, ее доказательство, базирующееся на усредненной по всем возмож-
ным канальным кодам вероятности ошибки, показывает, что почти все коды достаточно
большой длины будут хороши с этой точки зрения. Более того, поиски конкретных кодо-
вых правил, позволяющих достичь шенноновского предела, оказались тщетными вплоть
до момента открытия турбо–кодов в 1993, хотя множество важных и широко используе-
мых результатов было получено в ходе стремления к этой цели.
Очевидно, что современная теория кодирования слишком сложна, чтобы позволить
изложить даже ее начальные основы в небольшой главе. Все это оказывается еще более
печальным на фоне ключевой роли теории кодирования в глобальной информационной
технологии, в которой широкополосная связь является только одним из направлений.
Кроме того, роль канального кодирования в широкополосных системах чрезвычайно вы-
сока, поскольку большинство из них проектируются для работы в сложной помеховой об-
становке и, более того, многие из них сами создают сильные внутрисистемные помехи
(помехи множественного доступа (MAI) в асинхронном варианте CDMA). Влияние помех
MAI, в отличие от естественного (теплового) шума, не может быть преодолено только по-
средством «грубой силы», т.е. увеличением мощности сигнала, поскольку все пользовате-
ли обладают равными правами и выигрыш в отношении сигнал-помеха (SIR) одного из
них, достигнутый этим способом, оборачивается потерями для других (см. параграфы 4.5–
4.6). Последнее оставляет проектировщику только два способа преодоления MAI: увели-
чение показателя расширения или привлечение мощных канальных кодов. Руководствуясь
принципом рациональности, ограничимся рассмотрением в этой главы только проблем
кодирования, связанных с коммерческими 2G и 3G широкополосными стандартами
