Ипатов В.П. Широкополосные сигналы

Подождите немного. Документ загружается.

288

применимому к любой линейной системе (одним из примеров этого служит (8.26)), в z–

области передаточная функция

)(zh

замкнутой петли обратной связи выражается (учи-

тывая эквивалентность операций сложения и вычитания в двоичной арифметике) как [2,7]

)()(1

)(

zhz





где

)(zh

)(z

– передаточные функции разомкнутой петли и схемы обратной связи со-

ответственно. Рассматривая выход крайнего слева сумматора на рис. 9.10 как выход замк-

нутой петли, имеем

zgzgzgzzh

121

)(,1)(  

, так что

)(/1)(

zgzh



. По-

скольку поделенный битовый поток

)(/)(

zgzb

непосредственно подается на вход регист-

ра, то логическая схема формирования проверочных символов, определяемая полиномами

nlzg

,,2),( 

, может быть подсоединена к тому же регистру для дальнейшего обычно-

го сверточного кодирования. Резюмируя, в систематическом кодере с обратной связью би-

товый поток источника непосредственно определяет поток бит данных

)(

, тогда как

потоки проверочных символов

nlzu

,,2),( 

формируются той же логической схемой,

как и на рис. 9.3, но подсоединенной к регистру с обратной связью. Рис. 9.11 иллюстриру-

ет пример преобразования несистематического кодера, изображенного на рис. 9.4, в сис-

тематический.

Полная структура турбо–кодера включает два подобных систематических кодера и

перемежитель, как это показано на рис. 9.12 для кодеров компонент со скоростью

2/1

. В этой структуре отбрасывается «прямой» поток бит данных со второго компо-

нента кодера, а используются только потоки его проверочных бит. Таким образом, если

образующие сверточные коды имеют скорость

2/1

, то результирующий турбо–код

содержит два проверочных символа

на один бит данных

, т.е. имеет скорость

1

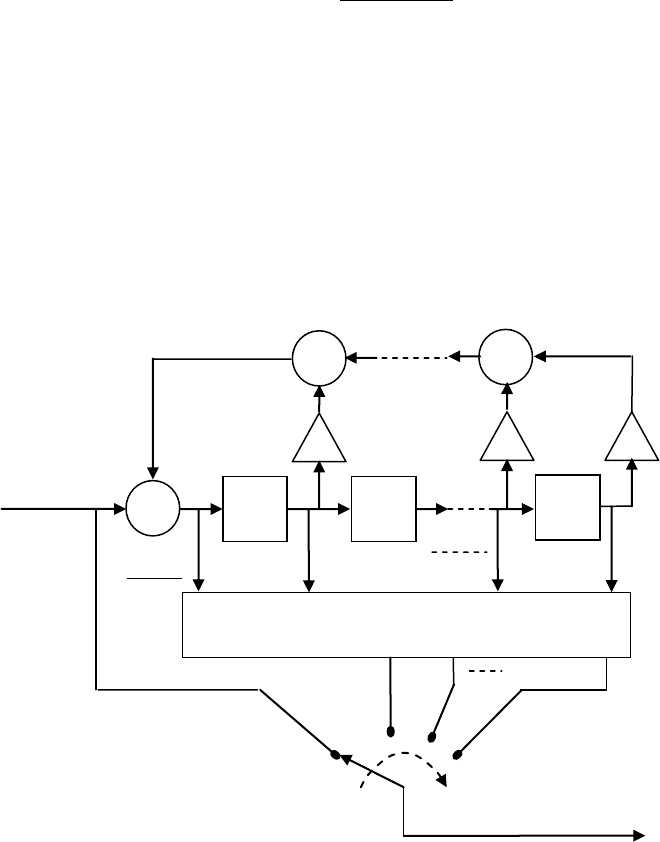
Рис. 9.10. Систематический сверточный кодер.

)(zb

)(

,,

Кодовые символы

,,

Логика формирования

проверочных символов

...),,(

289

3/1

. При желании его скорость может быть увеличена до

2/1

путем передачи только

одного проверочного символа на бит данных, выбираемого поочередно с кодеров компо-

нент. Перемежитель перемешивает биты данных в пределах блока длины I. Как правило,

для установки кодера первого компонента в нулевое состояние используется

1

хво-

стовых бит, и турбо–код трактуется как блоковый код, содержащий I информационных

бит.

9.4.2. Процедура итеративного декодирования.

Несмотря на то, что турбо–код состоит из двух сверточных кодов, его оптимальное

декодирование не может быть реализовано в виде двух независимых процедур Витерби,

поскольку пути на решетчатых диаграммах его компонентов связаны друг с другом вслед-

ствие кодирования одного и того же (хотя и с перемежением) потока данных. Открывате-

ли турбо–кодирования [95,96] предложили использовать итеративную версию правила

максимума апостериорной вероятности (МАП) (maximum a posteriori probability (MAP)).

Представленное ниже описание касается только основной ее идеи, отсылая заинтересо-

ванного читателя за деталями к [96,97].

Апостериорные вероятности

 

y0

 

y1

характеризуют правдоподоб-

ность одного или другого значения i–го бита данных, вычисленную на основе вектора на-

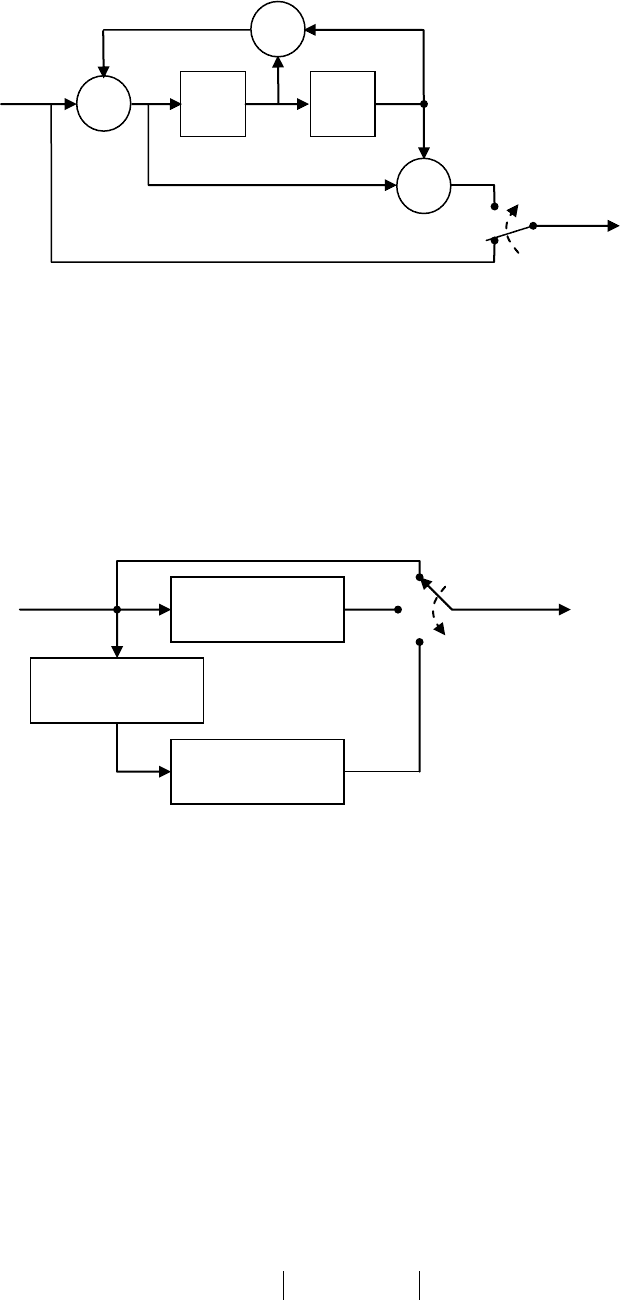
Рис. 9.11. Систематический сверточный кодер для кода из примера 9.3.1.

Биты источника

Символы кода

...,,

...,,,,

uuuu

...,,

Сверточный

кодер

Сверточный

кодер

Перемежитель

Биты данных

bu 

Рис. 9.12. Турбо–кодер.

Символы кода

290

блюдения

. Они содержат в себе полную информацию о

, доставляемую

и извле-

каемую из него. В случае достоверной связи одна их этих вероятностей близка к единице,

тогда как вторая почти равна нулю. Действительно, МАП декодер будет выдавать на вы-

ход в качестве оценки

i–го бита данных такое значение, которому отвечает большая

апостериорная вероятность, следуя правилу

 











. (9.11)

Рекуррентный алгоритм вычисления апостериорной вероятности значения бита

разработан в [98]. В рассматриваемой ситуации бит данных

фактически присутствует в

наблюдениях вследствие применения систематического кодирования. При непосредствен-

ной реализации рекуррентный МАП алгоритм вычисляет апостериорную вероятность

используя все ранее полученные наблюдения, включающие данный бит. После принятия

всех отсчетов наблюдения, он возвращается назад и пересматривает результаты, содер-

жащие информацию, извлеченную из наблюдений, поступивших после

. Таким образом,

после прохождения вперед и возвращения назад могут быть найдены апостериорные ве-

роятности для всех бит данных. Для реализации этого алгоритма необходимо знать ре-

шетку кода, канальные переходные вероятности и распределение априорной вероятности

)(

для каждого бита данных. Очевидно, что не возникнет никаких проблем при реали-

зации алгоритма в отношении каждого из двух компонент сверточных кодов, образующих

турбо–код. Однако основная идея турбо–кода состоит в кодировании одних и тех же пе-

ремеженных данных двухкомпонентным кодом, так что информация о

может быть вос-

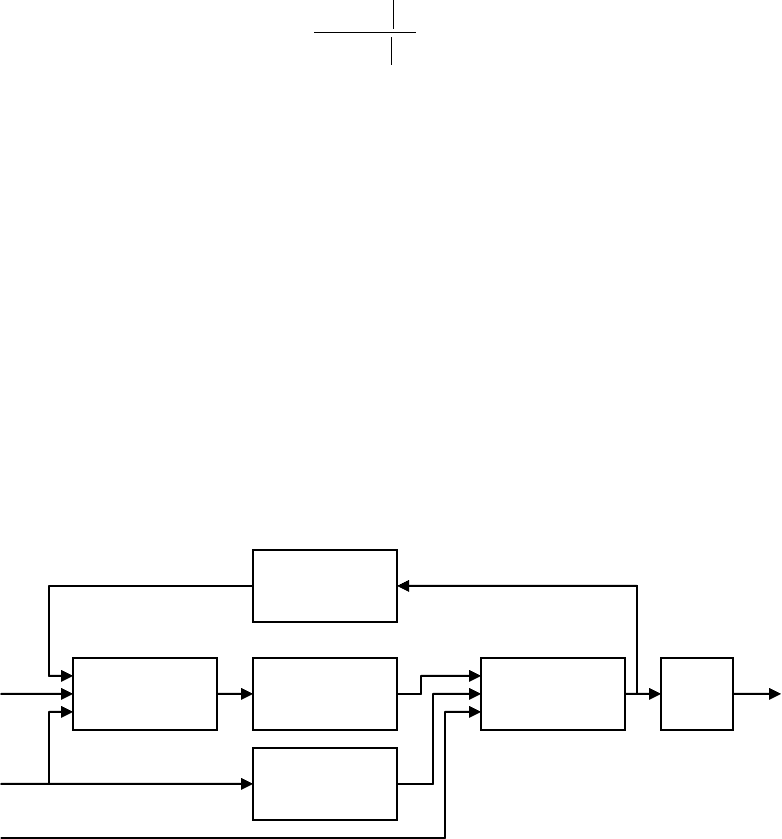
становлена совместно по обоим из них. Итерационный процесс, организованный, как по-

казано на рис. 9.13, удовлетворяет данному условию.

Полный вектор наблюдения на приемной стороне может быть разложен на три со-

ставляющих:

3,2,1,  l

lll

nuy

, где

iiM

buuuu 



),,,,( u

– вектор бит данных

непосредственно представлен в любом кодовом слове вследствие систематического ха-

рактера турбо–кодов,

, uu

– вектора избыточных символов первого и второго кодеров

соответственно, а

– вектор независимых выборок шума.

На первом шаге декодер первого компонента кода вычисляет апостериорные веро-

Декодер

1 –го кода.

Декодер 2–го

кода

Перемежи-

тель.

Перемежи-

тель.

Деперемежи-

тель.

)(







Рис. 9.13. Итеративный турбо–декодер.

291

ятности

),(

211

всех I бит данных

, использую наблюдения

,yy

, связанные с

проверочными символами и символами данных этого кода. В качестве исходной инфор-

мации используется а приори равномерное распределение

1,0,2/1)(



bbq

, посколь-

ку естественно считать равновероятными все образцы бит данных. После этого декодер

второго кода, вычисляющий апостериорные вероятности

),(

311

, может основывать-

ся не только на соответствующих наблюдениях

,yy

, но также на информации, достав-

ляемой первым декодером, используя его апостериорное распределение

),(

211

в ка-

честве априорного:

),()(

211

bpbq 

. В результате имеем первое приближение

)(

апостериорного распределения

)( y

. Поскольку на этом шаге первый декодер

не снабжается информацией от второго, то это положение исправляется на второй итера-

ции, когда первый декодер снова декодирует первый компонент кода, но при использова-

нии априорного распределения

)()(

bpbq 

. Продолжая подобным образом, после n–

го шага следующая аппроксимация

)( y

распределения

)( y

формируется вторым

декодером и используется первым декодером в качестве следующего априорного распре-

деления

)(

1 in



для выработки

),(

211



. Последнее в свою очередь, используется

вторым декодером как следующее априорное распределение

)(

1 in



для выработки сле-

дующей аппроксимации ожидаемой апостериорной вероятности

)(



и т.п. По-

скольку перемежитель меняет порядок следования бит данных перед подачей их на вход

второго кодера, перемежители аналогичным образом воздействуют на наблюдения

априорное распределение

),(

inn

bpq 

, подающиеся на второй декодер. Аналогично,

деперемежитель восстанавливает первоначальный порядок бит в схеме обратной связи,

передавая

)( y

с выхода второго декодера на вход первого. С учетом этих преобразо-

ваний все данные, обрабатываемые обоими декодерами, соединяются должным образом.

Обширное моделирование экспериментально подтвердило сходимость этих итера-

ций, однако теоретическое обоснование до сих пор остается под вопросом.

9.4.3. Характеристики.

Как упоминалось ранее, турбо–коды представляют собой первый пример регуляр-

ных кодов, обеспечивающих надежную передачу данных по каналу с ограниченной поло-

сой со скоростью, близкой к пропускной способности, и малой энергии на бит. Для иллю-

страции этого на примерах рассмотрим первоначально некоторые фундаментальные огра-

ничения при передаче данных с бинарной ФМ. На основании теоремы отсчетов любой по-

лосный сигнал с полосой W представим вектором размерности 2WT (см. параграф 2.3). В

случае использования бинарной ФМ каждый компонент такого вектора может принимать

только два значения, откуда следует, что в пределах заданного частотно–временного ре-

сурса WT число M бинарных ФМ сигналов подчиняется ограничению

2

, или, что

эквивалентно, может быть передано не более чем 2WT бит данных. Это ограничивает ско-

рость передачи, достижимую при бинарной ФМ в пределах полосы W, как

WTMR 2/)(log 

, что в свою очередь определяет границу скорости на один герц:

2/ WR

бит/сек/Гц. Рассмотрим теперь двоичный код со скоростью

2/1

, означаю-

щей, что только каждый второй компонент сигнального вектора переносит данные, тогда

как остальные предназначены для проверки символов (на один бит приходится два отсче-

та сигнала), так что отношение между скоростью и полосой будет

1/ WR

бит/сек/Гц.

292

Обратившись к границе Шеннона (1.2), можно заметить, что минимальное значение энер-

гии на бит, нормированной к спектральной плотности шума

/ NE

(что составляет поло-

вину отношения сигнал-шум по мощности на бит), необходимой для обеспечения безоши-

бочной передачи по АБГШ каналу с такой скоростью, составляет 0 дБ. Однако, имея дело

не с произвольным гауссовским каналом, а с каналом, входные символы которого ограни-

чены алфавитом бинарной ФМ (гауссовский канал с бинарным входом). Это ограничение

увеличивает минимальное отношение

/ NE

, отвечающее

1/ WR

бит/сек/Гц, до

0.19 дБ [97]. Турбо–код с длиной кодового ограничения 5 и длиной блока 65536, предло-

женный в [95,96], обеспечивает вероятность ошибки на бит





(это значение часто

используется в качестве практического критерия безошибочной работы беспроводной

системы) при

7.0/

NE

дБ, т.е. уступает пределу Шеннона только около 0.5 дБ. В мо-

мент опубликования этих работ данные результаты казались фантастическими, поскольку

длинная и безуспешная история заставила многих экспертов поверить, что отыскание ре-

гулярных правил кодирования, позволяющих работать вблизи границы Шеннона, является

безнадежной тратой времени. Вслед за оригинальными работами [95,96] были открыты

другие эффективные турбо–коды, как и последовательные коды конкатенации (см. биб-

лиографию в [97]).

Следует отметить, что в асимптотическом варианте

)/(

NE

поведение тур-

бо–кодов не отличается от сверточных при той же скорости и памяти, поскольку они не

обладают никаким преимуществом в смысле минимума расстояния. Обратившись к (2.23),

можно увидеть, что асимптотически (с ростом отношения сигнал-шум) эффект размноже-

ния

min

, т.е. числа сигналов с минимумом евклидова расстояния

min

относительно пе-

реданного сигнала, играет второстепенную роль по сравнению с собственно значением

min

вследствие экспоненциального уменьшения Q–функции с ростом отношения сигнал-

шум (чтобы убедиться в этом, достаточно взять логарифм от

). По этой причине зави-

симость

от

/ NE

чуть раньше или чуть позже приобретет характер ограничения, оп-

ределяемый

min

, которое аналогично для любого кода с одинаковыми значениями ми-

нимума расстояния. Данный эффект, однако, происходит при значениях отношения сиг-

нал-шум, обеспечивающих очень малую вероятность ошибки на бит, которые лежат зна-

чительно ниже диапазона практических требований. Объяснение тому, почему турбо–

коды гарантируют настолько высокое качество работы при низком отношении сигнал-

шум, заключается не в их большом значении минимума расстояния, а скорее в относи-

тельно малом числе слов, находящихся друг от друга на малом расстоянии, в частности

малом увеличении

min

в (2.23). Подобное перераспределение расстояний в направлении

большего числа слов, находящихся на большом расстоянии, по сравнению со сверточны-

ми кодами объясняется псевдослучайным перемежением бит данных, кодируемых вторым

компонентом кодера. Если образец данных оказывается неудачным с точки зрения фор-

мирования кодового слова с малым весом первым компонентом кода, то в результате пе-

рестановки он может оказаться достаточно отличным от исходного, что позволит второму

компоненту сформировать слово значительно большего веса.

9.4.4. Приложения.

Несмотря на короткую историю турбо–коды в настоящее время нашли широкое

применение и входят в состав спецификаций многих систем. Наибольший интерес в рас-

сматриваемом контексте представляет их вовлеченность в стандарты мобильных систем

третьего поколения. Спецификация UMTS включает турбо–коды со скоростью 1/3, осно-

ванные на двух компонентах сверточных кодов с длиной кодового ограничения 4 и пере-

межении переменной длины в диапазоне от 40 до 5114 [92,97]. В стандарте cdma2000 так-

293

же используются двухкомпонентные турбо–коды с длиной кодового ограничения 4 и об-

ластью перемежения, лежащей в диапазоне от 250 до 4090. Соответствующее выкалыва-

ние позволяет получить скорости 1/2, 1/3, 1/4 или 1/5 [69,97].

9.5. Канальное перемежение.

Проведенные выше анализ опирался на модель канала без памяти, в котором иска-

жающие действия канальной помехи, наносимые кодовым символам, были независимыми.

В реальных беспроводных каналах с эффектами затенения и замирания (см. параграф 3.5)

упомянутые аддитивные эффекты без памяти дополняются мультипликативными: сравни-

тельно медленными и распространяющимися на много кодовых символов спорадически-

ми падениями в уровне принимаемого сигнала. Метод, описанный ниже, является универ-

сальным, не зависящим от мягкого или жесткого метода декодирования, но для большей

прозрачности обсуждения положим, что используется процедура жесткого декодирова-

ния. Если АБГШ является единственной канальной помехой, то все ошибки в символах

являются независимыми и случайно распределенными на интервале кодовых слов. Паде-

ние уровня сигнала вследствие замирания вызывает группирование ошибочных символов

в пакеты или пачки. Очевидно, что если длина B пакета не превосходит корректирующей

(обнаруживающей) способности

)(

, то кодер без труда исправит (обнаружит) B оши-

бок, поскольку вид конкретного образца ошибок в пределах способности кода к контролю

над ошибками не играет роли. Однако природа замирания часто приводит к редким, но

достаточно длинным пакетам ошибок, так что выполнение условия

tB 

потребует ко-

дов с большим числом избыточных символов, т.е. малой скоростью и расточительным ис-

пользованием полосы. Эффективной и осуществимой на практике альтернативой является

очень популярное т.н. канальное перемежение (channel interleaving). Суть последней за-

ключается в том, что перед передачей символы кодового потока перемешиваются с целью

такого их распределения, при котором близко расположенные друг к другу по возможно-

сти разносятся на максимально большое расстояние, а те, которые исходно далеки, стано-

вятся близкими. На приемной стороне осуществляется процедура деперемежения, в ре-

зультате которой все кодовые символы возвращаются на свои исходные позиции. Если в

канале возникает пакет ошибок длины B, то искаженные им символы после деперемеже-

ния оказываются далеко разнесенными друг относительно друга, как если бы ошибки бы-

ли независимыми. Если используется блоковый код соответствующей длины и расстоя-

ния, то с большой вероятностью эти ошибки окажутся в различных словах и будут ис-

правлены декодером. При сверточных кодах вероятность их исправления снова окажется

хорошей, поскольку подобные коды исправляют многие образцы ошибок, включая и те,

которые превышают свободное расстояние, если они не группируются в слишком плот-

ные пакеты. Простейшей реализацией рассматриваемого метода служит перемежение в

рамках блока, заключающееся в записи символов по строкам квадратной матрицы, а счи-

тывание их по столбцам. Очевидно, что деперемежение символов осуществляется в об-

ратном порядке.

Перемежение является составной частью большинства современных беспроводных

систем связи, включая все стандарты мобильного радио 2–го и 3–го поколений.

294

Задачи.

9.1. Для передачи

32M

сообщений используется двоичный блоковый код длины

9n

. Сколько проверочных символов содержится в этом коде? Какова его скорость?

Сколько возможно лишних двоичных векторов наблюдения?

9.2. Двоичный блоковый код характеризуется минимумом расстояния Хэмминга

7

. Каким будет минимальное расстояние Евклида, если двоичные символы переда-

ются с помощью частотной модуляции не перекрывающимися импульсами энергии

9.3. Для передачи данных по ДСК используется двоичный блоковый код

}01110,11000,00011,10101{U

. Принят вектор наблюдения

)00110(Y

. В какое кодовое

слово будет декодирован вектор при исправлении ошибок? Каков будет ответ, если

)11011(Y

? Какова исправляющая и обнаруживающая способность этого кода?

9.4. Доказать утверждение 9.2.2.

9.5. Каким должно быть минимальное расстояние двоичного кода, исправляющего

вплоть до

ошибок и, кроме того, обнаруживающего вплоть до

tt 

ошибок?

9.6. Определить число двоичных векторов, обладающих весом не более чем

(объем двоичной сферы радиуса

9.7. Используя результаты задачи 9.6, доказать границу Гильберта: двоичный бло-

ковый код, обнаруживающий до

ошибок, существует всегда, когда

CM 2)1(







где M, n – число кодовых слов и длина кода соответственно.

9.8. Вычислить результат следующих операций над двоичными полиномами:

26322423

)1()1()1)(1()( zzzzzzzzf 

9.9. Раскрыть скобки в двоичном полиноме

)1( 

, где i – целое положительное

число.

9.10. Найти остаток от деления

 zz

на

 zz

над полем

)2(GF

9.11. Пусть

)(zg

– двоичный полином степени r. Доказать, что двоичный блоковый

код длины n, использующий его в качестве порождающего полинома (т.е. имеющий кодо-

вые полиномы вида

)()()( zgzbzu 

, где

)(zb

– произвольные двоичные полиномы степе-

ни не выше

1 rn

) является линейным.

9.12. Двоичный полином

1)(

 zzzg

– примитивен. Какова наибольшая длина

CRC кода на основе этого полинома, обнаруживающего вплоть до трех ошибок? Является

ли полином наблюдения

1)(

 zzzzy

ошибочным или нет? Что можно сказать о

295

полиноме

1)(

 zzzzy

9.13. Порождающими полиномами сверточного кода являются

1)(

zg

zzg 1)(

. Какова скорость и длина кодового ограничения порождаемого ими кода?

Изобразить схему кодера, нарисовать решетчатую диаграмму и определить свободное

расстояние кода.

9.14. Порождающими полиномами сверточного кода являются

1)( zzzg 

1)( zzg 

. Какова скорость и длина кодового ограничения порож-

даемого ими кода? Изобразить схему кодера, нарисовать решетчатую диаграмму и опре-

делить свободное расстояние кода.

9.15. Одним из двух порождающих полиномов сверточного кода является

1)( zzzg 

. Какой из полиномов

1)(

zg

zzg 1)(

или

1)( zzg 

лучше в

качестве второго порождающего полинома для получения наибольшего выигрыша от ко-

дирования? Чему равен максимальный выигрыш от кодирования? Какого типа выводы

следуют из этой задачи при сравнении систематического и несистематического кода?

9.16. Порождающими полиномами сверточного кода являются

1)( zzzg 

1)( zzg 

. Закодировать битовый поток 110110110110110… и объяснить, почему этот

код принадлежит классу так называемых катастрофических кодов, которые не рекомен-

дуется к практическому использованию?

9.17. Декодировать максимально возможное число бит при условии приема наблю-

дения 100101100011000 и порождающих полиномов сверточного кода

1)(

zg

zzg 1)(

9.18. Декодировать наблюдение 111111100000001111, если известно, что в качестве

порождающих полиномов сверточного кода используются полиномы задачи 9.14, а после

кодирования четырех бит данных кодер принудительно устанавливается в нулевое со-

стояние хвостовыми битами. Насколько далеко расположено декодированное слово от на-

блюдения? Если результат декодирования правилен, сколько ошибок исправил декодер?

9.19. Исправьте процедуру декодирования в примере 9.3.4, сохраняя все пути, вхо-

дящие в узел с одинаковыми метриками, как выжившие. Продолжите процедуру после

седьмого шага до первого шага, когда может быть осуществлена выдача бит данных. На

каком шаге это произойдет? Сколько бит данных выдается?

9.20. Битовый поток кодируется двоичным сверточным кодом с порождающими

полиномами

1)(

zg

zzg 1)(

. Двоичные символы передаются с помощью бинарной

ФМ

)11,10( 

. Канал связи является гауссовским и выходные отсчеты наблюдения

заданы вектором

)2,3,5,4,2,6,4,3,5.0,5.0( y

. Декодировать данное наблю-

дение с использованием жесткого и мягкого (основанного на вычислении корреляций на-

блюдения с путями по решетчатой диаграмме) алгоритма Витерби. Предположим, что два

последних кодовых символа отвечают хвостовым битам, устанавливающим кодер в нуль.

Объяснить различие (если оно есть) результатов этих двух процедур. Какая из них заслу-

живает большего доверия?

296

9.21. Желательно построить турбо-код, начинающийся сверточным кодом, зада-

ваемым порождающими полиномами

1)( zzzg 

1)( zzzzg 

. Изобра-

зить составные части кодера турбо-кода.

297

10. Некоторые достижения в развитии широкополосных

систем.

10.1. Многопользовательский прием и подавление помех

множественного доступа.

В параграфе 4.1 были рассмотрены два варианта принятия решения о данных в K–

пользовательской CDMA системе. Первый из них реализует оптимальную (максимально

правдоподобную) процедуру, осуществляемую т.н. многопользовательским приемником,

тогда как второй подразумевает использование однопользовательской или обычной про-

цедуры. Стандартный приемник воспринимает помеху множественного доступа (MAI),

как дополнительный случайный шум, полностью игнорируя детерминистскую природу

сигнатур и их корреляционные свойства. Напротив, многопользовательский алгоритм ис-

пользует априорные сведения о кодах сигнатур или, по крайней мере, их ансамблевые

корреляционные свойства. В рамках данного параграфа кратко обсудим идеи, лежащие в

основе многопользовательского приема, начиная с простейшего случая синхронной

CDMA.

10.1.1. Оптимальное (МП) правило многопользовательского приема для синхронного

варианта CDMA.

Для того чтобы освободить обсуждение от второстепенных деталей рассмотрим

простейшую, однако, и достаточно общую модель K–пользовательской CDMA системы с

прямым расширением спектра, включающую реальные сигнатуры и передачу данных с

помощью бинарной ФМ. Модель охватывает, среди других, любую систему с бинарными

сигнатурами и бинарной модуляцией данных. Как и в параграфе 7.2, в рамках данного

пункта рассмотрим полностью синхронизированный случай, когда как чипы, так и грани-

цы символов данных (бит) всех пользователей жестко связаны во времени. Последнее, на-

ряду с предположением о независимости последовательных бит данных любого пользова-

теля, позволяет ограничить интервал наблюдения длительностью единственного бита

TT 

. Тогда групповой сигнал K пользователей представим в виде





kkk

tsbAts

)();( b

, (10.1)

где аналогично (4.1)

0

– вещественная амплитуда k–го пользовательского сигнала,

),,,(

21 K

bbb b

– вектор бит данных K пользователей (битовый образец),

)(ts

– k–я

пользовательская сигнатура.

Как указывалось в параграфе 4.1, глобально оптимальная (МП) процедура диктует

искать оценку

)

(

21 K

bbb b

образца бит данных K пользователей

, как такое значе-

ние

, которое минимизирует евклидово расстояние (или его квадрат

),(

ysd

) между на-

блюдением

)(ty

и групповым сигналом (10.1). Вычисление

),(

ysd

аналогично (4.3) при-

водит к следующему результату

 



 



kllklk

kkk

bbAAzbAdttstyd

1 11

2)];()([),( ybys

, (10.2)

где





dttstyz

)()(

(10.3)