Ипатов В.П. Широкополосные сигналы

Подождите немного. Документ загружается.

278

пользует коды со скоростью

n/1

в качестве подсобного материала и удаляет некоторые

кодовые символы в соответствии с заранее назначенным образцом. При соответствующей

организации процедуры выкалывания происходит уменьшение числа кодовых символов

на бит данных, что обеспечивает достижение скорости

nk /

. Исходя из реализационных

возможностей, процедура выкалывания часто считается предпочтительной, подчеркивая

еще раз доминирующий интерес в отношении кодов со скоростями вида

n/1

. Следуя этой

тенденции, сконцентрируем наше внимание только на сверточных кодах со скоростью

n/1

Очевидно, что схема, содержащая регистр сдвига и отдельные сумматоры по моду-

лю два вместе со всеми их соединениями, представляет собой ничто иное, как фильтр с

конечным импульсным откликом (КИО) (finite impulse response (FIR) filter) (см. рис.6.20),

сигнал на выходе которого представляет собой свертку входного потока битов и импульс-

ной характеристикой фильтра, что объясняет название рассматриваемых кодов. Данный

факт лежит также в основе одного из способов формального описания сверточного коде-

ра. Свертка, связывающая кодовый символ

(т.е. появляющийся на выходе l–го сумма-

тора при поступлении

бита источника) с входным битовым потоком, определяется как











,,2,1;,1,0,

tti

nligbu 

, (9.6)

где

1

, если l–й сумматор соединен с t–й ячейкой памяти (

0t

соответствует входу

кодера) и

0

в противном случае;

0

при

0i

. В частотной области подходящим

инструментом для описания дискретных систем является z–преобразование, уже упоми-

навшееся в предыдущем параграфе. В z–области свертке соответствует произведение z–

преобразований, так что соотношение (9.6) может быть представлено эквивалентной фор-

мой

nlzgzbzuzu

,,2,1),()()(









, (9.7)

где







)(

zbzb

– z–преобразование входного потока бит, а

nlzgzggzg

lll

,,2,1,)(

 



(9.8)

– передаточная функция l–го КИО–фильтра (т.е. формирующая l–й кодовый символ), на-

зываемая также l–м порождающим полиномом (generator polynomial) сверточного кода.

Множество из n порождающих полиномов полностью определяет сверточный код, по-

скольку их ненулевые коэффициенты конкретизируют соединения сумматоров с регист-

ром сдвига.

Рис. 9.4. Сверточный кодер со скоростью 1/2.

Биты источника

Символы кода

...,,

...,,,,

uuuu

279

Пример 9.3.2. Кодер, изображенный на рис. 9.4, характеризуется порождающими

полиномами

1)( zzzg 

1)( zzg 

. Не трудно убедиться, что последовательно-

сти кодовых символов, приведенные в примере 9.2.1, могут быть получены из (9.7). 

Полагая

1)(

zg

, получаем систематический сверточный код, в котором биты ис-

точника данных занимают вполне определенные позиции. Однако проблема заключается в

том, что в рамках фиксированной структуры, изображенной на рис. 9.3, систематические

коды, как правило, не оказываются лучшими с точки зрения исправляющей способности

(см. задачу 9.15). Последнее обосновывает модификацию регистра сдвига сверточного ко-

дера в структуру с обратной связью, если свойство систематичности играет важную роль.

Более детально обсудим данный вопрос при ознакомлении с турбо–кодами в параграфе

9.4.1.

9.3.2. Решетчатая диаграмма, свободное расстояние и асимптотический выигрыш от

кодирования.

Регистр сдвига сверточного кодера обладает



возможными состояниями и

имеется только два состояния, в которые он может перейти из текущего состояния после

очередного такта. Именно значение входного бита источника

определяет выбор одного

из двух возможных переходов. Если на i–м тактовом интервале состояние регистра опре-

деляется, как

),,(

121 

iii

bbb 

, то следующее состояние будет либо

),,0(

21 

bb 

при поступлении на вход бита источника

0

, либо

),,1(

21 

bb 

, если

1

. Аналогично, регистр приходит в состояние

),,,(

11 

iii

bbb 

, если его предыдущее состояние было либо

)0,,,,(

221 

iii

bbb 

либо

)1,,,,(

221 

iii

bbb 

. Для схематического изображения всех деталей поведения

регистра адекватным инструментом служит решетка (trellis). Она включает две колонки

из



узлов, причем левая колонка отвечает текущему состоянию регистра, а правая –

следующему. Ребра (стрелки) выходят из каждого узла левой колонки и входят в некото-

рые два узла следующей, причем сплошные и пунктирные ребра показывают пути, соот-

ветствующие приходу бита нуля или единицы соответственно. Аналогично, в каждый узел

правой колонки входят два ребра, отмеченные или сплошной (нулевой входной бит), или

пунктирной (входной бит равен единице) линиями. Каждое ребро помечено n–разрядным

блоком, который представляет собой группу из n кодовых символов, выдаваемых кодером

в момент, когда входной бит источника переводит его из одного состояния в другое.

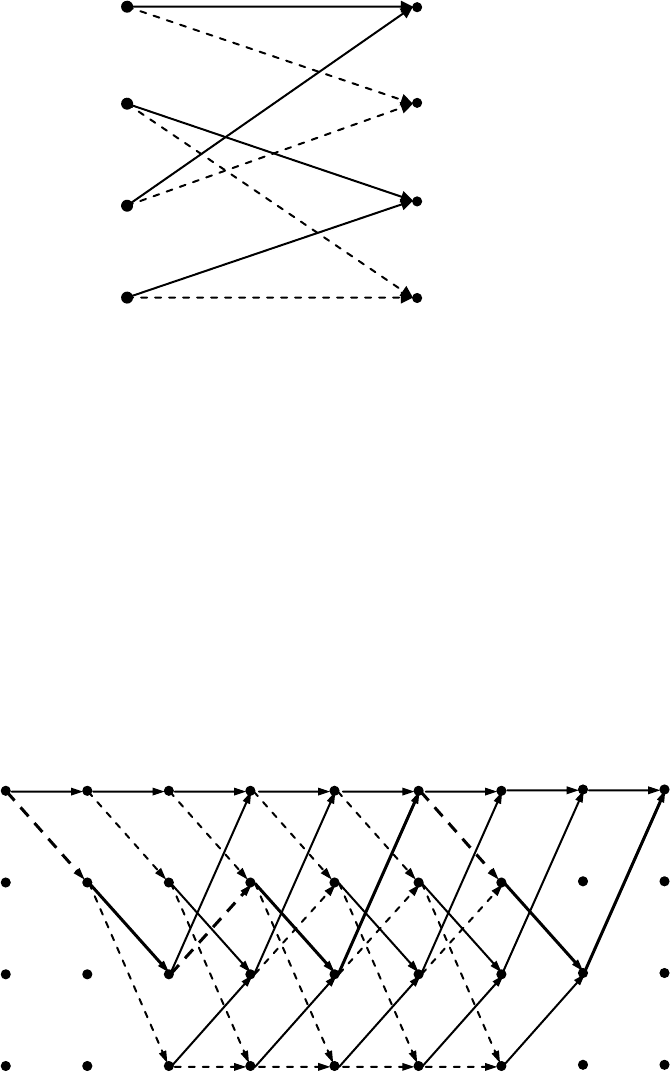
Нижеприведенный пример поясняет способ построения решетки для случая свер-

точного кодера на рис. 9.4.

Пример 9.3.3. Двухразрядный регистр сдвига может находиться в одном из четы-

рех возможных состояниях: (00), (10), (11) и (01), причем запись состояния ведется с ле-

вой ячейки памяти. На рис. 9.5 приведена решетка, построенная согласно выше приведен-

ному описанию. Например, ребро из состояния (10) в (01) отмечено сплошной линией, а в

состояние (11) – пунктирной. Ребро, идущее из состояния (11) в (01), помечено кодовыми

символами 01, поскольку при единицах в обеих ячейках и нулевым битом на входе верх-

ний сумматор на рис. 9.4 вырабатывает нулевой выходной сигнал, а нижний выдает еди-

ницу и т.п. 

В течение интервала каждого такта состояние кодера изменяется согласно движе-

нию вдоль какого-то ребра решетки, одновременно выдавая на выход кодовые символы,

которыми помечено данное ребро. Отслеживая этот процесс по диаграмме, подобно пред-

ставленной на рис. 9.5, необходимо производить скачки из правой колонки в тот же самый

узел левой колонки на каждом последующем шаге. Для избежания этого повторим решет-

280

ку столько раз, сколько необходимо, использую правую колонку текущего шага в качестве

левой для последующего шага. Тогда кодирование может быть отождествлено с движени-

ем вдоль полученной решетчатой диаграммы (trellis diagram), регулируемым текущим

входным битом, который направляет кодер по сплошному или пунктирному ребру в зави-

симости от его конкретного значения: нуля или единицы. Для иллюстрации сказанного

обратимся к рис. 9.6, на котором представлена решетчатая диаграмма кода из примера

9.3.1. Каждая последовательность–кандидат входных битов данных выбирает определен-

ный путь по решетчатой диаграмме, который можно отследить, например, для последова-

тельности

10100100}{ 

. Ее первый бит равен единице, что направляет кодер из узла

(00) в узел (10), выдавая выходные кодовые символы 11. Второй бит, равный нулю, пере-

водит кодер из узла (10) в (01), генерируя кодовые символы 10. Третий бит изменяет со-

стояние кодера с (01) на (10), выдавая на выход кодовые символы 00 и т.д. Жирной чертой

выделен результирующий путь, отвечающий кодовому слову 1110001011111011.

Ранее уже было отмечено, что сверточный код можно трактовать как блоковый код

соответственно большой длины. Кодовые слова этого блокового кода есть просто различ-

ные пути по решетчатой диаграмме, минимальное хэммингово расстояние среди всех их

пар дающее кодовое расстояние. В свою очередь, линейность кода упрощает задачу нахо-

ждения кодового расстояния: на основании утверждения 9.2.3 минимум расстояния между

)00(

)10(

)01(

)11(

)00(

)10(

)01(

)11(

Рис. 9.5. Решетка кодера на рис. 9.4.

(00)

(10)

(01)

(11)

Рис. 9.6. Решетчатая диаграмма кодера на рис. 9.4.

281

путями определяется наименьшим весом Хэмминга среди всех ненулевых слов. Предпо-

ложим теперь, что закодированный битовый поток заканчивается после некоторого боль-

шого (не меньше чем



) числа бит и дополняется

1

хвостовыми нулями для уста-

новки регистра в нулевое состояние. Реализованное на практике (одним из примеров слу-

жит cdmaOne) это дополнение не приведет к значительным затратам, если длина кодиро-

ванного потока бит во много раз больше длины кодового ограничения. С другой стороны,

введенное дополнение приведет к слиянию всех путей в один, который соответствует ну-

левому состоянию регистра, как показывает рис. 9.6 для кода из примера 9.3.1. Если те-

перь взять дополненный битовый поток, начинающийся с некоторого числа

нулей, за

которыми следует бит, равный «1», и переместить эти

начальных нулей в конец пото-

ка, то это будет означать простой сдвиг соответствующего пути на

шагов влево на диа-

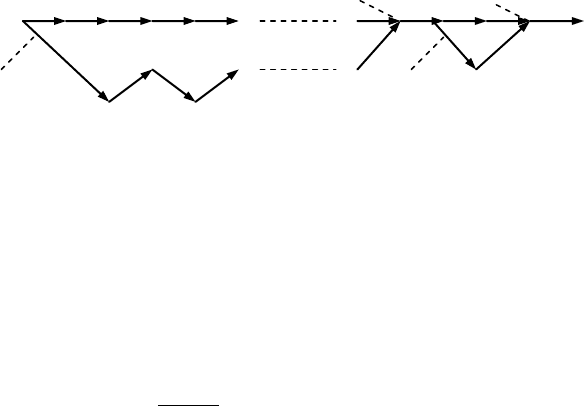
грамме без изменения его веса. После такого сдвига путь отклонится от нулевого пути на

самом первом шаге и сольется с ним не позднее, чем за

шагов до последнего хвостово-

го нуля. Вдоль этого пути могут произойти неоднократные возвращения к нулевому пути

и последующие отклонения от него (см. рис. 9.7), каждое из которых только увеличивает

вес пути, и поскольку целью является отыскание пути минимального веса, то любые от-

клонения от нулевого пути, кроме первого, должно игнорироваться. Суммируя все выше-

сказанное, заключаем, что для отыскания расстояния сверточного кода следует исследо-

вать только пути, отклоняющиеся от нулевого пути в начале решетчатой диаграммы и не

отходящие от него после первого объединения. В теории сверточных кодов эта величина

традиционно называется свободным расстоянием (free distance). Обозначив ее как

можно увидеть, например, что среди всех путей с единственным отклонением от нулевого

пути, изображенных на рис. 9.6, кодовое слово 11101100…, кодирующее битовый поток

100…, имеет минимальный вес, так что

5

. Очевидно, что свободное расстояние

гарантирует исправление любых















ошибок в символах (см. утверждение 9.2.2), од-

нако, как правило, исправляются также и многие образцы с большим числом ошибок. Су-

ществует только несколько примеров эффективных алгебраических правил сверточного

кодирования. Большинство же известных сверточных кодов с хорошей корректирующей

способностью были найдены в результате компьютерного поиска [31,33,93].

Вследствие специфичности алгоритмов кодирования аналитическое нахождение

всех возможных весов слов (весового спектра) произвольного сверточного кода оказыва-

ется не столь трудно, как в случае многих линейных блоковых кодов. В частности, непо-

средственно из решетки (или, что эквивалентно, диаграммы состояний) строится система

линейных уравнений, решение которой приводит к точному выражению для весового

спектра [2,7,93].

Выигрыш от кодирования, показывающий во сколько раз может быть уменьшена

энергия сигнала на бит или мощность сигнала в результате кодирования при фиксирован-

ной вероятности ошибки, является универсальным мерой для оценки эффективности того

Нулевой путь

1-е отклонение

2-е отклонение

1-е слияние

2-е слияние

Рис.9.7 Иллюстрация отклонения и слияния путей.

282

или иного кода. Это положение применительно к ортогональной сигнализации обсужда-

лось в параграфе 2.6 и отмечалось, что асимптотический выигрыш от кодирования в слу-

чае АБГШ канала определяется выигрышем в евклидовом расстоянии. При передаче с ис-

пользованием бинарной ФМ любое различие в символах двух сигналов увеличивает квад-

рат евклидова расстояния на величину, равную

, где

– энергия одного символа.

Имеется пара слов сверточного кода, имеющая

различных символов, и отсутствует

пара с меньшим различием (расстоянием Хэмминга). Следовательно, минимум квадрата

евклидова расстояния между словами сверточного кода, передаваемыми с помощью би-

нарной ФМ, составляет

sfcc

Edd 4

min,



. В то же время (см. параграф 2.6) аналогичная

характеристика при некодированной передаче составляет

Ed 4

min,



, определяя асим-

птотический выигрыш от кодирования сверточным кодом, как

G 

mi n,

где

– скорость кода, измеренная в бит/сим. Для кода из примера 9.3.1

5,2/1 

так что

5.2

или около 4 дБ. Напомним еще раз, что

выводится для АБГШ (не

ДСК) канала, другими словами, для случая применения мягкого декодирования. Жесткое

декодирование ухудшает эту цифру на 2..3 дБ в зависимости от параметров кода и отно-

шения сигнал-шум на символ [31,33].

9.3.3. Алгоритм декодирования Витерби.

Как уже упоминалось, среди причин широкой популярности сверточных кодов

особую роль играет существование эффективного алгоритма декодирования. Рассмотре-

ние его начнем со следующего положения.

Утверждение 9.2.5. Максимально правдоподобное жесткое декодирование с ис-

правление ошибок бинарного кода эквивалентно правилу минимума расстояния Хэммин-

га:

uyuyu

),(min),

( 



принимается за принятое слово. (9.9)

Как можно видеть, данное правило очень похоже на (2.3) с одним изменением: в случае

ДСК расстояние Хэмминга заменяет Евклидово расстояния, адекватное для АБГШ канала.

Для доказательства (9.9) достаточно заметить, что соотношение (9.1), переписанное в виде

dnd

ppP

)1(

)1()(

),(

),(),(





















yuyu

есть просто переходная вероятность ДСК, т.е. вероятность трансформации ДСК посланно-

го кодового вектора

длины n в двоичное наблюдение

. Поскольку перекрестная веро-

ятность ДСК

5.0p

, то переходная вероятность

)( uyP

есть убывающая функция рас-

стояния Хэмминга между наблюдением

на выходе ДСК и кодовым вектором

. Следо-

вательно, максимально правдоподобной оценкой

кодового слова является слово, бли-

жайшее по Хэммингу к

. 

Прямая реализация правила (9.9) для произвольного кода заключается в сравнении

M расстояний Хэмминга между наблюдением

и всеми кодовыми словами. Поскольку,

как правило, M достаточно велико, то такое решение может оказаться не осуществимым.

283

С другой стороны, для сверточных кодов вследствие их благоприятной структуры МП де-

кодирование не представляет особой трудности, по крайней мере, для умеренных значе-

ний длины кодового ограничения.

Процедура декодирования Витерби реализует максимально правдоподобную стра-

тегию в рекуррентной форме, последовательно осуществляя поиск пути по решетчатой

диаграмме, ближайший к двоичному наблюдению

. Каждый новый шаг декодирования

начинается с приема следующей группы из

символов наблюдения. На i–м шаге декодер

вначале вычисляет расстояние между n пришедшими символами наблюдения и каждым

ребром решетчатой диаграммы, а затем увеличивает расстояния всех путей, рассчитанных

за

1i

предшествующих шагов. Для произвольного кода расстояния можно вычислять

аналогично сразу же по приходу новых символов наблюдения, однако рекуррентная при-

рода сверточных кодов позволяет осуществить эту обычную вычислительную работу бо-

лее экономно по причине отбрасывания многих путей на каждом шаге.

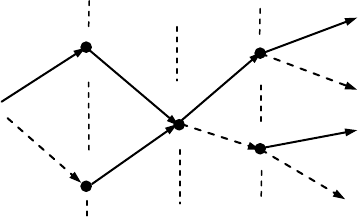
Рассмотрим все пути, проходящие через фиксированный узел A на i–м шаге, как

это показано на рис. 9.8. Продолжение любого пути после i–го шага не зависит от мар-

шрута прихода в A, так что все различные пути, достигающие A, могут в дальнейшем счи-

таться слившимися в один. Однако это означает, что из всех путей, проходящих через A и

продолжающихся после i–го шага, один, обладающий минимальным расстоянием от

вплоть до i–го шага, навсегда останется ближайшим к

, поскольку общее продолжение

внесет равный вклад во все расстояния. Тогда за чем продолжать вычисление расстояний

для остальных, если совершенно очевидно, что у них нет шансов оказаться в итоге бли-

жайшими к наблюдению? Вместо этого отбросим их, оставляя только один путь с мини-

мальным расстоянием, достигший узла A. Последний называется выжившим (survivor) пу-

тем и на данный момент будем считать, что имеется только один выживший путь для ка-

ждого из узлов решетчатой диаграммы на i–м шаге (см. комментарий ниже). Текущее, т.е.

вычисленное по всем символам наблюдения вплоть до i–го шага, расстояние узла A вы-

жившего пути от наблюдения

называется метрикой узла (node metric) A.

Теперь вспомним, что имеются только два ребра, входящие в любой узел, что и по-

казывает рис. 9.8 для некоторого узла A. Два ребра, входящие в него, исходят из узлов B,

C предшествующего этапа и, следовательно, продолжают выжившие пути B и C. Можно

вычислить расстояния двух путей, достигающих A, в результате вычисления только мет-

рик ребер, т.е. расстояний ребер от принятой группы из n наблюдаемых символов, и сум-

мирования их с метриками узлов B и C. Путь с меньшим расстояние считается выжившим

для узла A и запоминается вместе с его расстоянием (метрикой узла), тогда как другой от-

брасывается. По выполнению этих операций для всех узлов решетчатой диаграммы деко-

дер переходит к следующему этапу.

Рис. 9.8. Пути, проходящие через узел A на i-м шаге.

1i

1i

Шаги:

284

Резюмируя сказанное, декодер Витерби на каждом шаге вычисляет метрики ребер,

добавляет их ко всем метрикам узлов, накопленных ранее, а затем отбрасывает большее

расстояние из двух, ведущих к каждому узлу. Поскольку всего имеется



узлов (т.е.

состояний регистра), сложность декодера определяется только длиной кодового ограниче-

ния



и остается фиксированной вне зависимости от теоретически неограниченного чис-

ла кодовых слов (путей).

Возвращаясь к сделанному предположению о единственности выживающего пути

для каждого узла, отметим, что поскольку расстояние Хэмминга целочисленно, то всегда

существует вероятность того, что два пути, ведущие к одному и тому же узлу, обладают

одинаковыми текущими расстояниями относительно

. Возможны различные стратегии

преодоления неопределенности этого типа. Одна из них использует случайный выбор:

присвоение реверса честной монеты одному из путей и провозглашение его выжившим в

случае выпадания реверса при бросании монеты. Подобное действие, конечно, нарушает

оптимальность декодирования, хотя сопровождающие его энергетические потери, как

правило, незначительны. Альтернативой является признание обоих конкурирующих путей

выжившими и запоминание их до тех пор, пока дальнейшие шаги не разрешат неопреде-

ленность. Последняя стратегия сохраняет оптимальность декодирования ценой увеличе-

ния требуемой памяти.

Пример 9.3.4. Рассмотрим декодирование наблюдения

0100110000y

для кода

из примера 9.3.1. Рис. 9.9 иллюстрирует данный процесс с указанием метрик узлов, распо-

ложенных непосредственно около них, и кадров, содержащих пары принятых символов

наблюдения на текущем шаге. Декодер начинает процесс в предположении нулевого (т.е.

00) начального состояния кодирующего регистра. Начальные

21

шаги отвечают

переходному состоянию кодирующего регистра, когда только одна ветвь входит в каждое

состояние (см. рис. 9.9) и все пути оказываются выжившими. На первом шаге декодер

сравнивает первую группу из

2n

символов наблюдения с двумя ребрами, выходящими

из состояния (00). Согласно их расстоянию Хэмминга от группы символов 01 как сплош-

ное, так и пунктирное ребра решетки приобретают метрику, равную 1, которая приведена

рядом с ними. Следовательно, метрики двух узлов, до которых дошли ребра, становятся

равными единице. На следующем шаге расстояние измеряется между второй группой на-

блюдаемых символов 00 и двумя парами ветвей, исходящих из узлов (00) и (10), приводя к

метрикам, которыми помечены ветви. После добавления к метрикам узлов предшествую-

щего этапа они обновляют метрики узлов (00) и (10), а также образуют метрики еще двух

узлов (01) и (11). Начиная с третьего шага в любой узел решетчатой диаграммы рис. 9.9

входят по две ветви, означающие, что декодер должен решить какая из них выживает. На-

чиная с этого шага, откажемся от показа метрик ребер, чтобы не перегружать рисунок.

Как видно, на третьем шаге имеются два пути, ведущие к узлу (00). Их расстояния от на-

блюдаемых символов 010011 составляют величины, равные 3 и 2 соответственно. Первый

из них не выживает, и декодер отбрасывает его вместе с соответствующей метрикой, что

отражено перечеркиванием пути и отсутствием его на рисунке следующего этапа. Второй

путь является выжившим и запоминается со своей метрикой до следующего шага. Анало-

гичным образом декодер определяет выжившие пути и для остальных узлов. В ходе по-

следующих шагов процедура декодирования продолжается подобно рассмотренному, со-

храняя в памяти только





выживших путей, и каждая диаграмма на рис. 9.9 изо-

бражает только пути, выжившие на предшествующем этапе.

На 7–м шаге декодер впервые сталкивается с проблемой неоднозначности: два пути

приходят в узел (01) с одинаковыми расстояниями, как и в узел (11). Выбор выжившего

пути, иллюстрируемый рисунком, отражает его реализацию посредством подбрасывания

монеты. Аналогичные события происходят на 8–м и 9–м шагах. Читатель может убедить-

ся (задача 9.19), что любое альтернативное решение неопределенности не изменит окон-

чательного результата декодирования за исключением числа шагов, после которых воз-

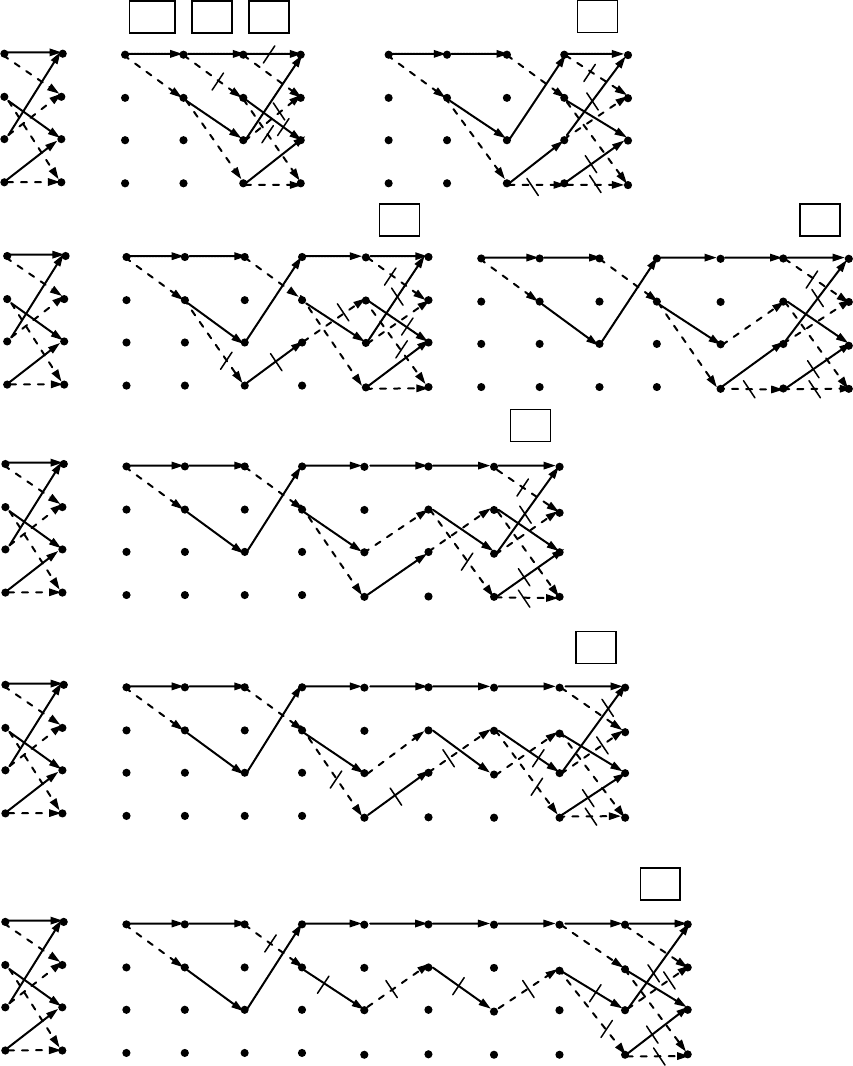
285

можно первое считывание декодированных бит (см. ниже).

Ситуация, возникшая после девятого этапа, является чрезвычайно важной: все пути

оказываются слившимися вплоть до седьмой группы наблюдаемых символов. Чтобы ни

произошло в дальнейшем, эта часть всех слившихся путей навсегда останется общей, оз-

начая, что биты данных, соответствующие этому участку, как раз теперь могут быть деко-

дированы. Таким образом, декодер выдает декодированные данные вида 1000000. Срав-

нивая кодовое слово

00001110110000u

, отвечающее указанному потоку бит данных, с

наблюдением

0100110000y

, можно заметить, что расстояние Хэмминга между ними

равно 2, и если переданное слово действительно было таким, каким его определил деко-

(00)

(10)

(01)

(11)

Этап:

(00)

(10)

(01)

(11)

Этап:

(00)

(10)

(01)

(11)

Этап:

(00)

(10)

(01)

(11)

Этап:

(00)

(10)

(01)

(11)

Этап:

Рис. 9.9 Динамика декодирования сверточного кода из примера 9.3.1.

286

дер, то были исправлены две ошибки в полном соответствии с величиной свободного рас-

стояния

5

. Аналогичные ситуации будут возникать и в дальнейшем, позволяя деко-

деру выдавать декодированные биты в процесс обработки потока наблюдаемых символов.

Очевидно, что выдача декодированных данных в случайные моменты слияния вы-

живших путей, как в вышеприведенном примере, выглядит не практично и более жела-

тельной представляется процедура регулярной выдачи данных. Неоднократно было про-

верено экспериментально и путем моделирования, что в течении i–го шага декодирования

сливающаяся часть всех выживших путей почти никогда не заканчивается после числа

бит данных

i 5

, так что решение о любом бите может регулярно приниматься с за-

держкой в

5

[94].

Очень важным свойством сверточных кодов, делающим их еще более привлека-

тельными, является сравнительная простота реализации мягкого декодирования. В самом

общем случае блокового кода с M кодовыми словами осуществление мягкого декодирова-

ния означает непосредственное вычисление M евклидовых расстояний или корреляций,

что представляется достаточно сложным алгебраически по сравнению с синдромным де-

кодированием. При значительных величинах M, типичных для множества приложений,

данный факт часто превращает указанную задачу в полностью не осуществимую. В то же

время платой за упрощения приемника, использующего жесткие решения, служат энерге-

тические потери, оцениваемые для АБГШ канала в 2 дБ: цифрой, рассматриваемой сего-

дня, как достаточно значительной. Обратимся вновь к алгоритму Витерби и просто заме-

ним расстояние Хэмминга евклидовым. Очевидно, что данная операция превратит деко-

дирование в его вариант с мягкими решениями, оптимальный для АБГШ канала. Тогда

метрики ребер и узлов в точности отвечают соответствующим евклидовым расстояниям

(или корреляциям). Подобная модификация ни в малейшей степени не затронет реализа-

ционные преимущества алгоритма Витерби. Действительно, метрики узлов вычисляются,

как и ранее рекурсивно, путем пошагового увеличения за счет метрик ветвей, а путь, вхо-

дящий в узел с худшей метрикой, чем альтернативный, снова может быть отброшен на

каждом шаге, как не выживший.

Конечно, цифровая реализация декодеров является наиболее предпочтительной,

подразумевая квантование входного наблюдения. Общепринятой является тенденция

классификации декодеров двоичных кодов, использующих квантование более чем на два

уровня, как декодеры с мягким декодированием. Углубленный анализ показывает, что в

большинстве случаев 3–битовое (8–ми уровневое) квантование достаточно для достиже-

ния почти потенциальных (характерных для непрерывной обработки) параметров [94].

9.3.4. Приложения.

В настоящее время известно множество эффективных сверточных кодов и диапа-

зон их использования в телекоммуникации чрезвычайно широк. В частности, 2G стандарт

cdmaOne и 3G стандарт UMTS использует коды с длиной кодового ограничения

9

скоростями

3/1,2/1 

, обеспечивая асимптотический выигрыш от кодирования

порядка 7.8 дБ [18,69,92]. 3G стандарт cdma2000 в дополнение к упомянутым выше ис-

пользует код с параметрами

4/1,9 

. Помимо их собственного значения сверточ-

ные коды служат основой для построения турбо–кодов, приближающих надежность пере-

дачи данных к пределу Шеннона, краткое обсуждение которых представлено ниже.

287

9.4. Турбо–коды.

Как уже упоминалось ранее в параграфе 9.1, несмотря на огромные усилия, при-

кладываемые в течение десятилетий с момента начала информационной теории Шеннона,

попытки отыскания регулярных правил кодирования, гарантирующих надежность переда-

чи близкую к пропускной способности канала, оставались безуспешными. В свете этого

открытие в 1993 г. турбо–кодов явилось впечатляющим прорывом, первоначально встре-

ченным телекоммуникационным сообществом с объяснимым недоверием. Однако в на-

стоящее время турбо–коды широко признаны в качестве эффективного средства обеспе-

чения высококачественной связи, особенно в условиях малого отношения сигнал-шум на

бит. Точная и компактная теория этого класса кодов остается скорее разрабатываемой,

чем действительно уже существующей. До сих пор интуиция в сочетании с обширными

компьютерными поисками играют значительную роль в получении многих результатов.

9.4.1. Кодеры турбо-кодов.

Другим названием турбо-кодов является параллельно сочетающие сверточные ко-

ды, что отражает основную идею алгоритма кодирования: два параллельных сверточных

кодера (компонента) кодируют один и тот же битовый поток источника [95,96]. Кодеры

компонентов, как правило, является идентичными, т.е. обладают одинаковыми длинами

кодового ограничения и множествами порождающих полиномов. Первый из них кодирует

данные непосредственно, тогда как перед поступлением на второй кодер битовый поток

данных подвергается перемежению. Данная операция состоит в перестановке по псевдо-

случайному закону бит данных в пределах блока фиксированной длины I.

Как было отмечено в параграфе 9.3.1, среди сверточных кодов, основанных на

структуре с КИО (см. рис. 9.3), отсутствует эквивалентность между систематическими и

несистематическими кодами, причем несистематические, как правило, являются более

мощными в смысле дистанционных свойств. В то же время принцип декодирования, свя-

занный с турбо-кодами и придающий им особую привлекательность, в большей степени

отвечает кодерам с систематическими компонентами. Применение структуры с бесконеч-

ным импульсным откликом (БИО) (infinite impulse response (IIR)) вместо КИО открывает

путь к формированию систематического сверточного кода, содержащего те же слова и,

следовательно, обладающего такими же дистанционными свойствами, как и несистемати-

ческий. Для объяснения этого факта начнем с рассмотрения кодера, изображенного на

рис. 9.3, который описывается множеством порождающих полиномов

nlzg

,,2,1),( 

, и

установим однозначное соответствие между двумя битовыми потоками

)(zb

)(

как

)()()(

zgzbzb 

. Обратимся затем к соотношению (9.7) и увидим, что для входного пото-

ка бит

)(

оно может быть представлено в виде

nlzg

zgzbzu

lll

,,2,1),(

)(

)()()(



, (9.10)

показывающем, что структура, способная осуществить деление битового потока источни-

ка

)(zb

на

)(

перед подачей на вход схемы с КИО, изображенной на рис. 9.3, будет

кодировать

)(zb

в те же сверточные слова, как и собственный КИО кодер. Единственное

отличие состоит в том, что кодовое слово, присваиваемое ранее

)(

, теперь перепри-

сваивается

)(zb

, что, учитывая равные права любого битового потока источника, не игра-

ет роли, если декодер знает этот новый порядок соответствия. Однако после подобной

операции все кодовые слова становятся систематическими, поскольку

)()(

zbzu 

. Ре-

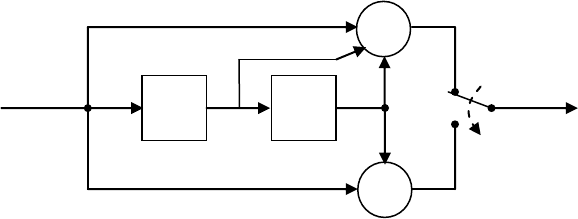
гистр с обратной связью, представленный на рис. 9.10, реализует деление на полином

1)(







zgzgzg

, где

1

. Действительно, согласно общему правилу,