Ипатов В.П. Широкополосные сигналы
Подождите немного. Документ загружается.

268
cdmaOne, UMTS и cdma2000. По этой причине приведенный ниже математический инст-
рументарий, обозначения и способ описания в максимально степени приспособлены соот-
ветствовать этой частной задачи наиболее экономичным и легким путем. Заинтересован-
ного в более глубоком охвате этого вопроса читателя отсылаем к книгам по теории коди-
рования (например, [31,33,91]).
Начнем с некоторой основной классификации канальных кодов. Первой характер-
ной чертой их различения является размер алфавита, согласно которому можно говорить о
бинарных, троичных и т.п. кодах. Хотя область применения недвоичных (например, Рида–
Соломона или Унгербоека) кодов в настоящее время достаточно широка, сконцентрируем
наше внимание только на двоичных кодах, используемых в вышеупомянутых специфика-
циях. Другим направлением группирования кодов служит способ отображения информа-
ционных данных в кодовые слова или кодовые вектора (т.е. последовательности кодовых
символов, переносящих передаваемое сообщение). Дело заключается в том, что любое ка-
нальное кодирование состоит во введении определенной избыточности в сообщение, ко-
торое увеличивает разнесение излученных сигналов друг относительно друга и, следова-
тельно, делает их менее подверженными перепутыванию. В зависимости от способа до-
бавления этой избыточности все канальные коды подразделяются на блоковые и древо-
видные. Характерной особенностью блоковых кодов является сегментация битового пото-
ка источника, которая состоит в делении на блоки из k информационных бит и представ-
лении каждого блока
kn
двоичными символами. В результате избыточные
kn
симво-
лов служат для защиты только k бит источника данного кодового слова. Кодовые слова
древовидных (например, сверточного) кодов обладают отличной структурой: непрерыв-
ный битовый поток источника кодируется в бесконечный поток кодовых символов (code-
stream) без фрагментации (см. детали в параграфе 9.3).
Достигнув приемной стороны, кодовое слово необходимо обратно отобразить в пе-
реданные биты данных. Данная операция называется декодированием. Фактически, благо-
даря модуляции, любое кодовое слово передается в канал в виде некоторого сигнала. При
прохождении АБГШ (либо другого стационарного) канала сигнал подвергается искаже-
нию шумом, мгновенные отсчеты которого непрерывны. В случае гауссовского шума оп-
тимальная (максимально правдоподобная) стратегия решения приемника эквивалентна
правилу решения по минимуму евклидова расстояния (см. параграф 2.1), которое означает
принятие за истинный сигнала, ближайшего к полученному наблюдению. Такая непосред-
ственная процедура заканчивается получением декодированных бит данных и носит на-
звание (наряду с многочисленными приближениями) мягкого декодирования. Сложность
алгоритмов мягкого декодирования послужила причиной частого применения альтерна-
тивного варианта, называемого жестким декодированием. Данный метод декодирования
включает два этапа: на первом из них принимаются решения по всем индивидуальным ко-
довым символам и, в результате, наблюдение оказывается демодулированным в вектор,
состоящий из символов, принадлежащих кодовому алфавиту (в рассматриваемом случае –
двоичному). Некоторые символы, полученного таким образом двоичного наблюдения, мо-
гут оказаться ошибочными, и тогда весь демодулированный вектор, возможно, будет от-
личаться от всех кодовых слов. Второй этап заключается в отыскании среди всех допус-
тимых кодовых слов одного максимально правдоподобного, т.е. отвечающего наибольшей
вероятности трансформации каналом в текущее демодулированное двоичное наблюдение.
Подобная процедура декодирования, заканчивающаяся, как правило, принятием решения
об истинности некоторого конкретного кодового вектора, называется исправлением оши-
бок. В качестве альтернативы декодирование может ограничиться только проверкой те-
кущего двоичного наблюдения: является ли оно подлинным кодовым словом, либо про-
изошли какие-то ошибки вследствие разрушительного действия канала. Тогда, если дво-
ичное наблюдение принадлежит множеству разрешенных кодовых слов, оно обратно ото-
бражается соответствующей последовательностью бит данных. В противном случае реги-
стрируется факт неудачной передачи, и приемник либо запрашивает передатчик о повторе
269
сообщения (как в случае систем с активным запросом), либо пытается восстановить его
путем интерполяции предыдущих и последующих сообщений. Этот тип декодирования,
называемый обнаружением ошибок, характерен при применении блоковых кодов в совре-
менных коммерческих беспроводных широкополосных системах, и следующий параграф
сфокусирован на форматах кодирования, связанных с работой по обнаружению ошибок.
9.2. Блоковые коды, обнаруживающие ошибки.
9.2.1. Двоичные блоковые коды и способность к обнаружению ошибок.
Предположим, что блок
110
,,,
k
bbb
представляет собой k бит источника, которые
необходимо закодировать двоичным кодовым словом
),,,(
110
n
uuu u
длины
kn
.
Все
k
2
комбинаций из k бит источника полагаются возможными, что означает существо-
вание
k
M 2
кодовых слов. В каждом кодовом слове
kn
двоичных символов являются
избыточными в том смысле, что только k символов необходимо для однозначного ото-
бражения M сообщений источника в двоичные вектора. Эти избыточные символы наде-
ляют кодовые слова большей различимостью друг от друга, обеспечивая тем самым луч-
шую сопротивляемость воздействию шума. Множество всех
k
M 2
слов длины n назы-
вается (n, k) блоковым кодом. Жесткое декодирование, т.е. демодуляция непрерывного
наблюдения в двоичное, отвечает модели двоичного симметричного канала (ДСК) – bi-
nary symmetrical channel (BSC), трансформирующего входные
1,0u
в противоположные
выходные двоичные символы
uy
с переходной (crossover) (или символьной ошибкой
(symbol error)) вероятностью p. Прилагательное «симметричный» подчеркивает одинако-
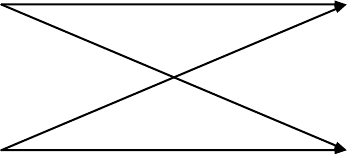
вые вероятности переходов «0» в «1» и наоборот (см. рис.9.1).
Предположим, что
),,(
110
n
yyy y
– двоичное наблюдение на выходе ДСК. Ес-
ли вектор
y
не совпадает ни с одним из M кодовых векторов
u
, то приемник считает, что
имеются ошибочные символы (обнаружение ошибок). В противном случае выделяются k
бит данных, отвечающих оцененному кодовому слову
yu
ˆ
. Очевидно, что если передан-
ным является слово
0
u
, а двоичное наблюдение совпадает с другим кодовым словом, т.е.
0
ˆ
uyu
, то имеет место не обнаруживаемая ошибка, а выделенные биты не отвечают
переданным.
Введем еще несколько определений. Расстоянием Хэмминга
),( gf
H
d
между двумя
векторами
),,,(
110
n
fff f
и
),,,(
110
n
ggg g
одинаковой длины n называется чис-
ло позиций, на которых вектора имеют отличные элементы
ii
gf
. Весом Хэмминга
)(f
H
w
вектора
f
называется число его ненулевых компонент. Если, например,
y
u
0
1
1
0
p1
p1
p
p
Рис.9.1. Модель двоичного симметричного канала

270
)11001(),01011( gf
, то
2),( gf
H
d
, а
3)( f
H
w
. Непосредственно можно убедиться,
что
)(),( gfgf
HH
wd
и
),()( 0ff
HH
dw
, где
0
– нулевой вектор.
Предположим, что передается кодовое слово
u
. ДСК преобразует его в отличное
фиксированное кодовое слово
v
(вызывая, тем самым, не обнаруживаемую ошибку и вы-
давая неправильные биты данных, соответствующие
v
), если ошибки в символах про-
изойдут на всех
),( vu
H
d
позициях, где
u
и
v
отличаются, и не будут повреждены на
),( vu
H
dn
позициях, где символы отличаются. Тогда для ДСК без памяти, т.е. канала, в
котором все символьные ошибки независимы, можно считать, что вероятность
)( uvy P
вышеупомянутого события будет
),(),(
)1()(
vuvu
uvy
HH
dnd
ppP
. (9.1)
Поскольку
2/1p
(в противном случае можно было бы просто переобозначить
выходные символы «0» и «1»), то для уменьшения вероятности перепутывания кодовых
слов
u
и
v
расстояние Хэмминга между ними должно быть максимально возможным.
Рассмотрим теперь расстояния Хэмминга
),( vu
H
d
между всеми различными кодовыми
векторами кода U. Обозначим наименьшее среди них как
H
d
и назовем его (минималь-
ным) кодовым расстоянием кода U:
),(min
,
vu
vu
vu
H
U
H
dd
. (9.2)
Передаваемым может оказать любое кодовое слово и для минимизации риска перепуты-
вания двух ближайших кодовых векторов расстояние между ними, т.е. кодовое расстояние
H
d
, должно быть максимально возможным. В итоге приходим к следующему утвержде-
нию:
Утверждение 9.2.1. Код U способен обнаруживать любые
d
t
и менее ошибки в
символах (вплоть до
d
t
ошибок), если и только если кодовое расстояние
1
dH
td
.
Действительно, возьмем код с
dH
td
, и выберем пару ближайших кодовых век-
торов
vu,
. Если
H
d
символов
u
, отличных от аналогичных вектора
v
, будут искажены,
то
u
превратиться в
v
, означая, что существует образец с не более, чем
d
t
ошибками, ко-
торый не обнаруживается. И наоборот, если расстояние между любыми кодовыми векто-
рами превосходит
d
t
, то не существует образца с
d
t
или менее ошибками, который
трансформирует кодовое слово в любое другое.
Аналогичным образом можно доказать следующее положение (задача 9.4).
Утверждение 9.2.2. Код U способен исправлять
c
t
и менее ошибочных символов,
если и только если его кодовое расстояние
12
cH
td
.
9.2.2. Линейные коды и их полиномиальное представление.
Будем трактовать двоичные кодовые символы
}1,0{
как элементы двоичного ко-
нечного поля
)2(GF
(см. параграф 6.6) и рассмотрим посимвольные линейные операции
над кодовыми словами кода U, подчиняющиеся арифметическим правилам
)2(GF
. Оче-
видно, что существует только одна не тривиальная операция этого типа, а именно, посим-
вольное сложение в
)2(GF
:
vuvu ),,,(),,,,(
110110 nn
vvvuuu
),,,(
111100
nn
vuvuvu
. Например, если
)010110(),100111( vu
, то
)110001( vu
. Посимвольное вычитание не играет самостоятельной роли и просто по-
вторяет сложение, поскольку в
)2(GF
отрицание элемента есть сам элемент. Аналогично,
271
посимвольное умножение на скаляр из
)2(GF
(т.е. на 0 или 1) любого кодового слова пре-
вращает его либо в нулевой вектор, либо не изменяет его совсем.
Двоичный код U называется линейным, если сумма любого числа кодовых векто-
ров снова дает кодовый вектор, принадлежащий U. Данное название следует из того фак-
та, что подобный код образует векторное (линейное) пространство над полем
)2(GF
[31,33,91], хотя эта концепция и не находит серьезного применения в дальнейшем изло-
жении. Любой линейный код U длины n содержит нулевой вектор (т.е. с n нулевыми ком-
понентами) в качестве кодового, поскольку сумма произвольного кодового вектора, вхо-
дящего в U, с самим собой в точности дает нулевой вектор:
0uu
. Следующее положе-
ние служит объяснением одной из причин особенного интереса к линейным кодам.
Утверждение 9.2.3. Кодовое расстояние линейного кода U равно минимальному
весу Хэмминга среди всех ненулевых кодовых слов:
)(min
0
u
u
u
H
U
H
wd
. (9.3)
Для доказательства этого положения достаточно произвести подстановку
)(),( vuvu
HH
wd
в (9.2) и заметить, что разность
uvu
вновь кодовое слово U.
Как показывает соотношение (9.3), отсутствует необходимость проверки всех
2/)1( MM
различных векторных пар для определения кодового расстояния линейного кода, содер-
жащего M слов. Достаточно «взвесить» M–1 ненулевых кодовых векторов, т.е. осущест-
вить в M/2 раз меньшее число тестов, что демонстрирует, учитывая, как правило, значи-
тельное число слов M, чрезвычайно значительный выигрыш.
Для более быстрого понимания идеи конструирования обнаруживающих ошибки
кодов для 2G и 3G беспроводных стандартов значительную помощь может оказать поли-
номиальное описание линейных кодов.
Сопоставим кодовому слову
),,,(
110
n
uuu u
кодовый полином
)(zu
относи-
тельно переменной z, упорядоченный как
0
2
2
1
1
)( uzuzuzu
n
n
n
n
,
где по соглашению принимается, что
1
0
z
. Указанное полиномиальное представление,
широко используемое в теории кодирования, представляет собой просто форму z–
преобразования, лежащего в основе анализа дискретных линейных систем, обработки
дискретных сигналов, цифровой фильтрации и т.д. [2, 7]. Однозначное соответствие меж-
ду множествами кодовых слов и кодовых полиномов означает, что сумма двух кодовых
полиномов
)(),( zvzu
линейного кода U снова является кодовым полиномом того же кода.
В частности, если
1
0
1
0
)(,)(
n
i
i
i
n
i
i
i
zvzvzuzu
– кодовые полиномы слов
vu,
линей-
ного кода U, то
1
0
)()()(
n
i
i
ii
zvuzvzu
кодовый полином слова
U vu
, где сложе-
ние коэффициентов подчиняется правилам поля, которому они принадлежат, т.е. в нашем
случае полю
)2(GF
.
Полиномиальная арифметика, используемая в анализе и синтезе кодов, включает
еще две операции: умножение и деление с остатком. Правила этих операций универ-
сальны независимо от полей, которым принадлежат полиномиальные коэффициенты, но,
имея дело с двоичными кодами, будем пользоваться двоичной арифметикой. Рассмотрим
произвольный (не обязательно кодовый) двоичный (т.е. с коэффициентами из
)2(GF
) по-
лином
)(za
. Наибольшая степень z в этом полиноме, содержащая ненулевой коэффици-
ент, называется степенью
)(za
с обозначением
)(deg za
. Пусть
)(),( zbza
– два двоичных
полинома, причем
nzbmza )(deg,)(deg
. Тогда их произведение
)()( zbza
является по-
линомом степени
nm
, полученным в результате распространения коммутативного
)(
ii
azaz
и дистрибутивного законов на операции, включающие формальную перемен-
272
ную z и объединяющие вместе коэффициенты одинаковых степей z:
))(()()(
0
1
10
1
1
bzbzbazazazbza
n
n
n
n
m
m
m
m
nm
k
k
k
i
iki
nm
nmnm
nm
nm
zbabazbabazbabazba
0 0
001001
1
11
)()(
.
Очевидно, что
nmnm
zzz
, все операции над
ii
ba ,
выполняются в
)2(GF
, а в последней
внутренней сумме коэффициенты
ii
ba ,
, индексы которых становятся отрицательными
или превосходят степень полинома должны быть положены равными нулю. Возьмем, на-
пример, двоичные полиномы
1)(,1)(
234
zzzbzzza
, тогда их произведение
1)()(
236
zzzzzbza
.
Алгоритм деления делимого
)(za
на делитель
)(zb
с остатком осуществляется сле-
дующим образом:
)()()()( zrzbzqza
, (9.4)
где
)(zq
является частным, а
)(zr
– остатком от деления. Единственность
)(),( zrzq
га-
рантируется соотношением
)(deg)(deg)(deg zbzqza
и
)(deg)(deg zbzr
. Алгоритм
(9.4) подобен «школьному» правилу деления целых чисел с остатком, в котором степени
полиномов заменяют целые величины. Одним из вариантов реализации этой операции яв-
ляется «длинное деление», т.е. последовательное вычисление остатка и деление его на де-
литель до тех пор, пока степень остатка станет меньше степени делителя. На первой ите-
рации
)(zb
умножается на z, возведенную в степень, уравнивающую степень произведе-
ния со степенью делимого
)(za
. Вычитание (эквивалентно сложению в
)2(GF
) получен-
ного произведения из
)(za
приводит к первому остатку, играющему на второй итерации
роль делимого, и т.д. Проиллюстрируем это на примере.
Пример 9.2.1. Пусть
1)(,1)(
234
zzzbzzza
. Применим алгоритм длин-
ного деления:
1
1
1
11
2
2
2
234
342
z
z
zz
z
zzz
zzzz
После двух итераций имеем
zzrzzq )(,1)(
2
, так что деление с остатком приводит к
следующему результату
zzzzzz )1)(1(1
2234
.
Как и в случае целых чисел, можно сказать, что
)(za
делится на
)(zb
(или
)(zb
де-
лит
)(za
), если остаток равен нулю, т.е.
)()()( zbzqza
.
Рассмотрим теперь линейный код U длины n со всеми кодовыми полиномами, де-
лящимися на фиксированный полином
)(zg
степени
1r
. Тогда любой кодовый полином
U представим в виде
)()()( zgzbzu
, и, поскольку имеется
rn
2
различных множителей
)(zb
, обеспечивающих степень произведения не больше
1n
, то такой код может вклю-
чать не более чем
rn
2
кодовых слов. Действительно, всегда возможно с одинаковыми
273
затратами пойти другим путем и построить код с этим максимальным числом слов, т.е.
при заданном полиноме
)(zg
фиксированной степени r передать
rnk
информацион-
ных бит. Для этого достаточно использовать
rnk
бит данных
110
,,,
k
bbb
в качестве
коэффициентов полинома данных
0
2
2
1
1
)( bzbzbzb
k
k
k
k
и построить соот-
ветствующий кодовый полином как произведение
)()()( zgzbzu
. Тогда
k
2
различным k–
битовым блокам данных однозначно соответствуют такое же число кодовых полиномов
степени не выше чем
1n
. Линейность подобного кода легко проверяется (задача 9.11). В
подобной конструкции полином
)(zg
называется порождающим полиномом (generator
polynomial) кода U. Отметим, что число избыточных или проверочных символов такого
кода всегда равно r, т.е. степени порождающего полинома.
Когда полином данных
)(zb
непосредственно умножается на порождающий поли-
ном
)(zg
, тогда кодовое слово, отвечающее полиному
)()()( zgzbzu
, является несисте-
матическим, т.е. биты данных в нем не выделены явным образом. Для построения систе-
матического кода, в котором, например, последние k двоичных символов являются ин-
формационными битами, а
knr
первых – проверочными символами, необходимо
осуществить определенную перегруппировку в кодовых словах. После подобной опера-
ции полное множество кодовых слов останется тем же и только отображение бит данных в
кодовые слова поменяется. Умножим полином данных
)(zb
на
knr
zz
, придя к поли-
ному
)(zbz
kn
степени не выше
1n
. Если остаток
)(zr
от деления произведения на
)(zg
отбрасывается (или добавляется к
)(zbz
kn
в двоичном случае), то оно становится дели-
мым на порождающий полином
)(zg
, т.е. превращается в кодовый полином. Последний
)()()( zrzbzzu
kn
отвечает систематическому кодовому слову, поскольку биты данных в точности являются
последними k коэффициентами
)(zbz
kn
, а
)(zr
степени меньшей, чем
knr
не может
их затронуть.
Пример 9.2.2. Построим кодовое слово линейного (5,2) кода с порождающим по-
линомом
1)(
23
zzzg
при битах данных вида
1,1
10
bb
. Тогда
1)( zzb
,
34
)( zzzbz
kn
, а после деления на
)(zg
получаем остаток
zzr )(
. Суммирование
)(zbz
kn
с остатком приводит к кодовому полиному
)()(
34
zzgzzzzu
, соответст-
вующего систематическому кодовому слову, последними двумя символами которого яв-
ляются биты данных.
9.2.3. Вычисление синдрома и обнаружение ошибок.
Предположим, что по ДСК передается слово
u
линейного кода U. На выходе эле-
менты двоичного наблюдения
y
, искаженные каналом, будут отличаться от переданных
символов, что может быть записано как
euy
, (9.5)
где
e
– вектор ошибок, состоящий из нулей и единиц на местах, которые отвечают не ис-
каженным и искаженным символам соответственно. Например, если слово
)01011(u
из
примера 9.2.2 трансформировано ДСК в наблюдение
)11110(y
, то вектор ошибок
)10101(e
. Аналогично кодовым словам наблюдение
),,,(
110
n
yyy y
и вектор оши-
бок
),,,(
110
n
eee e
могут быть представлены в полиномиальной форме
274
0
2
2
1
1
)( yzyzyzy
n
n
n
n
и
0
2
2
1
1
)( ezezeze
n
n
n
n
. Тогда (9.5)
примет вид
)()()( zezuzy
.
Пусть
)(zg
– порождающий полином кода U. Остаток
)(zs
от деления полинома
наблюдения
)(zy
на
)(zg
называется синдромом. Поскольку любой кодовый полином де-
лится на
)(zg
, то синдром повторяет остаток от деления полинома ошибок
)(ze
на
)(zg
.
Следовательно, ненулевой синдром всегда свидетельствует о наличии ошибок в наблюде-
нии
y
и обнаружение ошибок может быть реализовано как вычисление синдрома наблю-
дения
y
и принятие решения о наличии ошибок при ненулевом синдроме.
Очевидно, что не все образцы ошибок обнаруживаемы, и любой не обнаруживае-
мый вектор ошибок всегда является некоторым кодовым вектором. Действительно, если
)(ze
является кодовым полиномом, то он делится на
)(zg
и синдром равен нулю. С дру-
гой стороны, нулевой остаток говорит только о том, что
)(ze
делится на
)(zg
, но любой
полином степени не выше, чем
1n
, делящийся на
)(zg
, является кодовым полиномом.
Пример 9.2.3. Предположим, что передаваемое кодовое слово
)01011(u
(5,2) ли-
нейного кода трансформировано ДСК в
)11001(y
, т.е. произошла двукратная ошибка.
Деление
1)(
4
zzzy
на
1)(
23
zzzg
приводит к ненулевому синдрому
2
)( zzs
,
сигнализирующему о наличии ошибок. С другой стороны, если бы наблюдение было бы
)11101(y
, что соответствовало бы трехкратной ошибке, синдром оказался бы равным
нулю:
)()1(1)(
24
zgzzzzzy
, т.е. неспособным обнаружить такой образец
ошибки.
Иногда способность линейного кода обнаруживать ошибки характеризуется долей
не обнаруживаемых образцов ошибок в их общем числе. Поскольку всего возможно
n
2
векторов ошибок и только
k
2
, повторяющие кодовые вектора, не обнаруживаемы, то ука-
занная доля составляет
rkn
22
)(
.
Только что рассмотренные линейные коды, построенные на основе порождающих
полиномов, известны как циклические коды или укороченные циклические коды. Когда
они используются только для обнаружения (а не для исправления) ошибок, они часто на-
зываются циклическими избыточными кодами (cyclic redundancy codes (CRC)).
9.2.4. Выбор порождающих полиномов для CRC.
Поскольку доля необнаруженных ошибок экспоненциально падает с ростом числа
проверочных символов, то это может стимулировать использование порождающих поли-
номов высоких степеней. Однако следует напомнить, что проверочные символы являются
избыточными и увеличение их числа сверх рационального уровня может оказаться расто-
чительным. Как правило, CRC используются на более высоких уровнях системного про-
токола для проверки качества кадров данных, восстановленных на физическом уровне, т.е.
после использования ресурсов значительно более мощных исправляющих ошибки кодов.
Вследствие этого символьные ошибки, встречаемые CRC, достаточно редки и совершено
маловероятно, чтобы в кодовом слове с сотнями символов произошло более нескольких
ошибок. Таким образом, обнаружение трехкратных ошибок на кодовое слово часто счита-
ется удовлетворительным. Опишем процедуру синтеза CRC, удовлетворяющего данному
требованию.
Возьмем двоичный примитивный полином
)(
1
zg
степени m (см. параграф 6.6).
Важным фактом, доказанным в алгебре расширенных полей, является то, что примитив-
ный полином степени m никогда не делит бином
1
l
z
ненулевой степени
12
m
l
275
[30,32]. Тогда можно доказать следующее положение.
Утверждение 9.2.4. Линейный код U с порождающим полиномом
)()1()(
1
zgzzg
степени m обнаруживает все ошибки кратности до трех, если длина ко-
да
12
m
n
.
Вследствие линейности кода U (см. (9.3)) и утверждения 9.2.1 необходимо только
доказать, что минимальный вес ненулевого слова U не меньше четырех. Любой кодовый
полином
)(zu
, делящийся на
1z
, может быть представлен в виде
)1)(()( zzqzu
. Хотя
z является формальной переменной, последнее равенство сохранится после подстановки
1z
в обе его части, приводя к результату
0)1(
021
uuuu
nn
, означающему
четность числа ненулевых элементов слова, т.е. четность его веса. Полагая существую-
щим слово веса два с ненулевыми i–м и j–м символами
)( ij
, имеем кодовый полином
)1()(
ijiij
zzzzzu
, который не делится на
)(
1
zg
, поскольку последний, являясь
неприводимым, не может содержать z в качестве множителя, и не делит
ij
z
1
)12(
m
nij
как примитивный. Следовательно, наименьший вес ненулевого слова U
будет четыре.
Теперь выбор соответствующего порождающего CRC полинома очевиден. Если
желателен код длины n, тогда просто следует найти примитивный полином
)(
1
zg
степени
)1(log
2
nm
и построить порождающий полином в виде
)()1()(
1
zgzzg
.
Коды CRC этого типа есть ничто иное, как популярные коды Хэмминга (либо уко-
роченные при
12
m
n
) с исключенными словами нечетного веса. В альтернативном
применении они используются для исправления любой однократной и обнаружения лю-
бой двукратной ошибок.
Пример 9.2.3. Несколько CRC кодов используются в 2G и 3G спецификациях
[18,69,92]. Показательным примером может служить код, используемый всеми тремя
стандартами (cdmaOne, UMTS и cdma2000), который обладает порождающим полиномом
вида
)()1(1)(
1
51216
zgzzzzzg
, где
1)(
23412131415
1
zzzzzzzzzg
– примитивный полином. Аналогично, по-
рождающие полиномы других CRC кодов этих стандартов (степеней 30, 24 и т.п.) пред-
ставляют собой произведение бинома
1z
и примитивного полинома.
276
9.3. Сверточные коды.
Сверточные коды находят широкое применение в современных телекоммуникаци-
ях как эффективное средство обеспечения надежной передачи данных по каналам с шу-
мами. Входя в состав более общего класса древовидных кодов, в рамках его они отлича-
ются линейностью алгоритмов кодирования. Различие между сверточными и блоковыми
кодами до некоторой степени размыто: любой сверточный код может трактоваться как
блоковый код соответственно большой длины. Более разумно рассмотреть особенности и
причины чрезвычайной популярности сверточных кодов в их рекуррентной форме, позво-
ляющей реализовать значительно более практичные по сравнению с другими процедуры
декодирования с исправлением ошибок (алгоритм Витерби).
9.3.1. Сверточный кодер.
Идея сверточного кодирования в общих словах может быть описана следующим
образом. Возьмем блок (вектор) из
с
последовательных бит источника и линейно преоб-
разуем его в
1n
выходных двоичных кодовых символов, занимающих временной интер-
вал, равный длительности одного бита источника. Линейность по отношению к векторам с
компонентами из поля
)2(GF
означает просто суммирование по модулю два выбранных
компонентов. После этого обновим блок бит источника, включив в него один новый и ис-
ключив один наиболее старый. Снова имеем блок из
с
бит источника, задержанный от-
носительно исходного блока на один бит (и содержащий
1
c
предшествующих бит и
один новый), который кодируется n новыми кодовыми символами. Данная процедура не-
прерывно повторяется раз за разом, каждый момент времени вовлекая один новый бит и
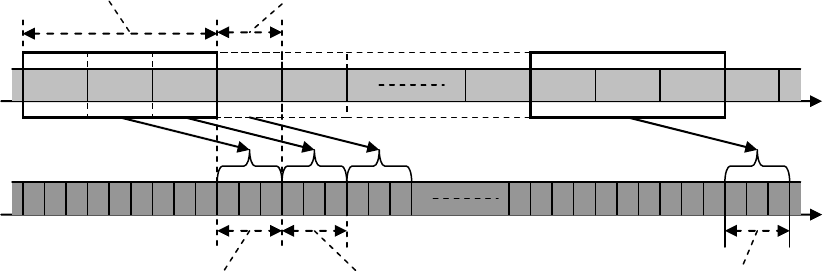
отбрасывая старейший. Рис. 9.2 иллюстрирует указанную процедуру для параметров
3,3 n
с
: кодер как будто просматривает битовый поток источника через скользящее
окно шириной
c
и кодирует все биты, которые в текущий момент видит, в n кодовых
символов. После каждого шага процедуры окно сдвигается на длительность одного бита
источника и выполняется следующий шаг. Число бит источника, определяющих кодовые
символы на одном шаге, называется длиной кодового ограничения (constraint length). Опи-
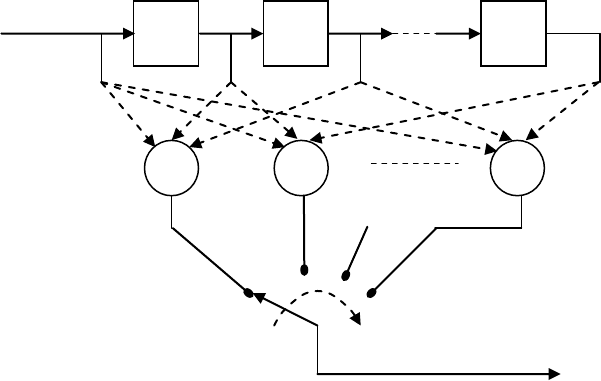
санный выше принцип может быть реализован структурой, представленной на рис. 9.3,
где регистр сдвига, состоящий из
1
c
ячейки памяти, хранит
1
c
предшествующих
бит источника. Вместе с поступающим битом они подаются в линейную логическую цепь,
содержащую n сумматоров по модулю два. Выход каждой ячейки памяти и вход кодера
T одного бита
Окно в
c
бит
Битовый поток
Кодовый поток
n
символов кода
n
символов кода
n
символов кода
Рис. 9.2. Иллюстрация сверточного кодирования.
277
может быть, а может и не быть (что объясняет обозначение связей пунктирной линией)
соединены с каждым сумматором, причем схема соединений определяет конкретную за-
висимость выходных кодовых символов от
c
бит источника, т.е. правило кодирования.
При поступлении на вход текущего бита источника
i
b
на выходах сумматоров параллель-
но появляются n кодовых символов
n
iii
uuu ,,,
21
. После каждого такта битовый образец в
регистре смещается вправо на одну ячейку, подготавливая цепь к формированию сле-
дующих n кодовых символов. Выходной ключ в течение одного бита поочередно подклю-
чается к выходам n сумматоров и преобразует параллельную форму представления кодо-
вых символов в последовательную, создавая выходной кодовый поток
,,,,,,,,
1
2
1
1
10
2
0
1
0
nn
uuuuuu
. Видно, что в устойчивом состоянии кодер на рис.9.3 на каж-
дый новый бит источника отвечает формированием n кодовых символов (см. также
рис.9.2), так что скорость кода
c
R
, измеренная в битах на один кодовый символ, равна
n/1
. Нижеприведенный пример поможет лучше понять принцип сверточного кодирова-
ния.
Пример 9.3.1. Рис. 9.4 иллюстрирует реализацию сверточного кодера с длиной ко-
дового ограничения
3
c
и скоростью
2/1
c
R
. Входные биты
,,
10
bb
порождают два
потока кодовых символов
,,
1
1
1
0
uu
и
,,
2
1
2
0
uu
, которые затем мультиплексируются та-
ким образом, что
1
i
u
и
2
i
u
занимают соответственно четные и нечетные позиции в общем
кодовом потоке. Например, битовый поток
10100100}{
i
b
порождает последователь-
ности
11011111}{
1
i
u
и
10001101}{
2
i
u
, которые затем мультиплексируются в кодо-
вый поток
1110111110001011)},{(
21
ii
uu
.
Естественно возникает следующий вопрос: возможна ли при сверточном кодирова-
нии скорость
c
R
, отличная от
n/1
, т.е. равная
nk /
, где
nk 1
? Существуют два класси-
ческих способа решения этой задачи. Первый состоит в обобщении вышеприведенного
принципа: на каждом шаге
c
k
, а не
c
, бит линейно преобразуются в n кодовых симво-
лов, после чего k наиболее старых бит (вместо одного) заменяются k новыми и кодер пе-
реходит к следующему шагу. Второй способ, называемый выкалыванием (puncturing), ис-
1
2
1
c
Рис. 9.3. Сверточный кодер.
+
+
+
1
2
n
Биты источника
Кодовые символы
,,
10
bb
,,
1
1
1
0
uu
,,
2
1
2
0
uu
,,
10
nn
uu
,,,,,
1
10
2
0
1
0
uuuu
n
