Ипатов В.П. Широкополосные сигналы
Подождите немного. Документ загружается.

228
7.4. Сигнатуры для асинхронного варианта CDMA, получаемые времен-
ным сдвигом.
Во многих реальных ситуациях взаимные временные сдвиги асинхронных сигнатур
могут изменяться только в пределах ограниченного диапазона. Конечность канальной за-
держки распространения с одной стороны и геометрия системы с другой являются наибо-
лее типичными факторами, устанавливающими эти ограничения. Для их детализации об-
ратимся к обратному каналу сотовой системы мобильной связи. Локальное время (такто-
вая частота) активной МС синхронизировано с принятым сигналом БС и характеризуется
задержкой
относительно времени БС, определяемой расстоянием
D
между БС и МС,
как
cD/
1
, где
c
– скорость распространения света. Поскольку сигнал, передаваемый
конкретной МС, достигает приемника БС с той же самой задержкой, то общий временной
сдвиг сигнала, дошедшего до БС, относительно времени БС составляет
cD/22
12
.
Пусть
max
D
– максимальное расстояние, при котором интенсивность принимаемого сиг-
нала достаточна для приема БС. Сильное ослабление при распространении (см. параграф
4.6) допускает игнорирование сигналов, которые пришли с расстояний, значительно пре-
вышающих радиус соты
c
D
. Последнее позволяет использовать следующую грубую
оценку для максимального расстояния
c
DD
max
. Тогда максимальное значение
2
со-
ставляет
cD
c
/2
, и сигналы мобильных станций, расположенных от БС на расстоянии от
нуля до
c
D
, достигают ее с задержками, принадлежащими диапазону
]/2,0[ cD
c
. Кроме
того, существуют многолучевые копии сигналов, так что общая ширина
max
окна, охва-
тывающего задержки всех многолучевых сигналов, увеличивается на величину канальной
задержки распространения
ds
:
dsc
cD /2
max
, где
ds
может быть максимизировано
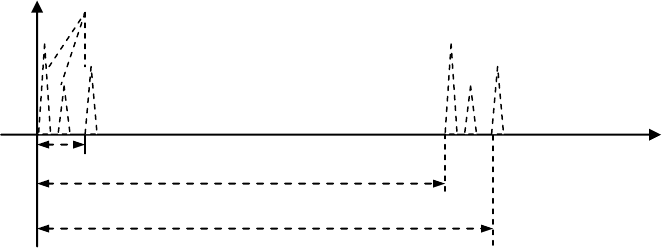
по всем возможным местоположениям МС. Рис. 7.16 служит иллюстрацией к приведен-
ному обсуждению. Сигнал некоторой конкретной МС может оказаться как опережающим,
так и задержанным по отношению к некоторому другому сигналу МС, а все многолучевые
копии сигнала любой МС потенциально используемы приемником БС (RAKE обработка,
см. параграф 3.7). Следовательно, полный диапазон возможных взаимных временных
сдвигов между любыми многолучевыми копиями любых сигнатур оказывается равным
],[
maxmax
, где
dsc
cD /2
max
.
Очевидно, что в подобных обстоятельствах следует заботиться о соблюдении вто-
рого и третьего условий (7.43) только в пределах диапазона действительно возможных
значениях
m
. Выразим величину
max
в округленном до целого числе
max
m
чипов:
t
0
ds
cD
c
/2
max
Многолучевые копии сигнала
Рис. 7.16. Изменение времени достижения БС сигналом с МС.
229
maxmax
m
. Тогда диапазон значений
m
, где следует выполнять требования (7.43),
определяется как
],[
maxmax
mm
. Возьмем теперь последовательность
}{
,1 i
a
периода
)1(
max
mKL
и используем в качестве K сигнатур ее циклически сдвинутые одна отно-
сительно другой копии на величину
1
max
m
позиций:
,1,0,1,;,,2,1,
)1)(1(,1,
max
iKkaa
mkiik
,
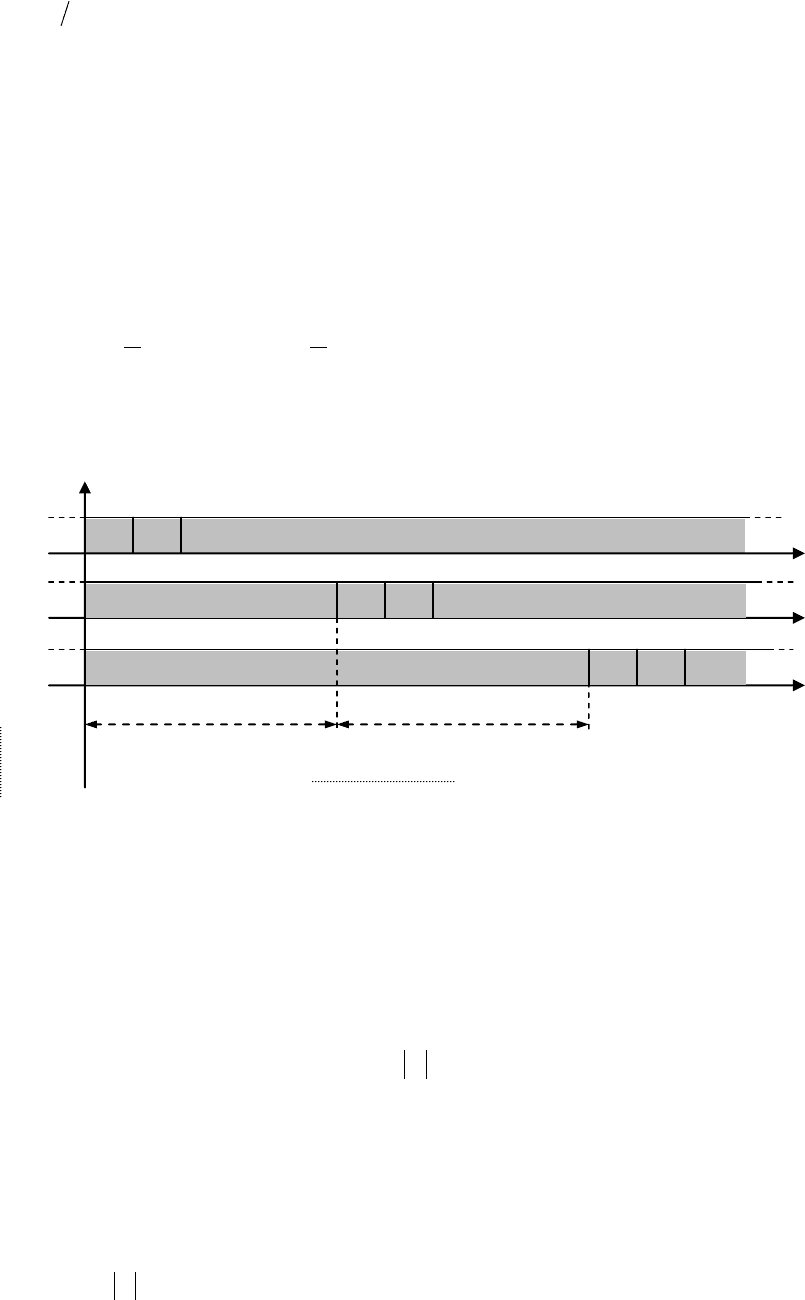
как показано на рис. 7.17. Очевидно, что все корреляции между образованными таким об-
разом сигнатурами будут выражены в терминах АКФ
)(
11
m
исходной последовательно-
сти
}{
,1 i
a
. Оценка ВКФ
k
–й и
l
–й сигнатур приводит к следующему результату
1
0
*
)1)(1(,1)1)(1(,1
1
0
*
,,
maxmax
11
)(
N
i
mmlimki
N
i
milikkl
aa
L
aa
L
m
,
или
])1)([()(
max11
mmlkm
kl
. (7.47)
Предположим теперь, что исходная последовательность
}{
,1 i
a
обладает либо иде-
альной, либо достаточно хорошей периодической АКФ
)(
11
m
. Первая возможна, напри-
мер, для троичных или многофазных последовательностей (см. параграф 6.11), тогда как
любая минимаксная бинарная последовательность (см. параграфы 6.7, 6.9) может служить
в качестве примера последней. Идея заключается в том, что все боковые лепестки
)(
11
m
является пренебрежимо малыми. Тогда при
max
mm
аргумент в квадратных скобках
(7.47) обращается в нуль по модулю L только в случае
lk
и
Lm mod0
, что отвечает
основному лепестку
k
–й сигнатуры. Для любой другой комбинации
mlk ,,
правая часть
соотношения (7.47) соответствует боковому лепестку
)(
11
m
, уровень которого полагает-
ся несущественным. Таким образом, доказано, что соответствующие сдвиги копий исход-
ной последовательности с хорошей периодической АКФ образуют ансамбль, для которого
выполняются условия псевдослучайности (7.43) во всем диапазоне значений взаимных
сдвигов сигнатур
max
mm
. Отсюда непосредственно следует, что этот ансамбль дости-
гает (при идеальной
)(
11
m
) или очень близко приближается к наименьшему уровню
(7.40) усредненных нежелательных эффектов, обусловленных помехами MAI и многолу-
чевого распространения, или, что эквивалентно, границам Велча (7.36), (7.35).
Пример 7.4.1. Рассмотрим систему с длительностью чипа
1
мксек, числом поль-
1
max
m
0,1
a
1,1
a
0,1
a
1,1
a
0,1
a
1,1
a
1-я сигнатура
2-я сигнатура
3-я сигнатура
Рис.7.17. Сигнатуры, образованные сдвигом во времени исходной последовательности.
1
max
m
230
зователей
60K
, канальной задержкой на распространение
20
ds
мксек и радиусом
соты
15
c
D
км. В этом случае
120/2
max
dsc
cD
мксек, а
120
max
m
. Ансамбль
сигнатур может быть построен на основе начальной последовательности
}{
,1 i
a
, период
которой должен быть равным
726012160)1(
max
mKL
. Поскольку
}{
,1 i
a
должна
иметь хорошую периодическую АКФ, то в роли подходящих кандидатов могут выступать
троичная последовательность с идеальной АКФ длины
8011L
, бинарная
m
–
последовательность длины
819112
13
L
или последовательность Лежандра с
7283L
. Тогда 60 сигнатур будут образованы как циклические копии
}{
,1 i
a
, сдвинутые
друг относительно друга на 121 чипов. Очевидно, что на длину последовательности не на-
кладывается верхний предел, и, возможно, разумнее выбрать ее больше с соответствую-
щим увеличением сдвига между сигнатурами, чтобы гарантировать некоторый резерв
безопасности.
Обратные каналы стандартов 2-го поколения cdmaOne (IS-95) и 3-го поколения
cdma2000 представляют хороший пример реализации данной версии асинхронного вари-
анта CDMA [69]. Бинарная
m
–последовательность чрезвычайно большой длины
12
42
L
, расширенная еще на один символ, используется в качестве исходной, а кон-
кретные пользовательские сигнатуры всех мобильных станций представляют собой ее со-
ответствующие циклические копии. Псевдослучайные свойства
m
–последовательности
совместно с сигнатурными сдвигами, превосходящими возможные изменения времени
прихода сигнала на приемник БС, гарантируют минимальный (см. (7.40)) уровень мощно-
сти помех MAI и многолучевости на выходе коррелятора.

231
7.5. Примеры ансамблей минимаксных сигнатур.
Ансамбли сигнатур, рассмотренные в предшествующем параграфе, могут быть
признаны адекватными только в ситуациях, когда взаимные временные сдвиги пользова-
тельских сигналов полностью контролируются системой и могут быть удержаны в рамках
предсказанного диапазона. Если же это не выполняется, то асинхронный CDMA, основан-
ный на использовании сдвинутых копий одной и той же последовательности, подвержен
возникновению коллизий: сигнал одного из пользователей может приобрести задержку, не
позволяющую отличить его от сигнала некоторого другого пользователя. Последнее мо-
жет служить основанием для использования ансамблей минимаксных сигнатур, т.е. таких
ансамблей, корреляционный максимум которых достигает или приближается к границам
(7.45) или (7.46). Поскольку корреляционный пик минимаксного ансамбля получен в ре-
зультате максимизации на всем периоде, то его малое значение (достигнутое за счет дос-
таточно большой длины
L
) обеспечивает близость корреляционных свойств ансамбля
идеальным (7.43), гарантируя псевдослучайность сигнатур.
Обзор всех известных минимаксных ансамблей занял бы достаточно большой объ-
ем, так что ограничимся лишь кратким обсуждением тех из них, которые либо имеют ши-
рокое практическое использование, либо оказываются наиболее показательными среди
других. Читатель, заинтересованный в более подробном изложении, может обратиться к
[9, 67, 70].
7.5.1. Бинарные частотно-сдвинутые m–последовательности.
Возьмем бинарную
}1{
m–последовательность
}{
,1 i
a
периода
12
n
L
и исполь-
зуем ее в качестве сигнатуры для первого пользователя. Остальные
1K
сигнатур фор-
мируются посимвольным умножением
}{
,1 i
a
на дискретные гармоники частот
KkLk ,.3,2,/)1(
:
Kki
L
ik
jaa
iik
,,2,1;,1,0,1,,
)1(2
exp
,1,
. (7.48)
Тогда квадрат модуля периодической ВКФ k–й и l–й последовательностей запишется как
2
1
0
,1,1
2
1
0
*
,,
2
,
)(2
exp)(
L
i
mii
L
i
milikklp
L
ilk
jaaaamR
. (7.49)
Первоначально рассмотрим случай
Lm mod0
, т.е.
1
2
,1,1,1
imii
aaa
. Тогда, если
lk
, соотношение (7.49) определяет основной лепесток АКФ k–й сигнатуры, т.е.
2
2
,
)0( LR
kkp
. Если же
lk
, то сумма в (7.49) есть сумма всех корней из единицы сте-
пени L, которая равняется нулю (см. параграф 6.11.2). Теперь пусть
Lm mod0
. Тогда,
согласно свойству сдвига и сложения m–последовательности (параграф 6.11),
timii
aaa
,1,1,1
для некоторого t, и квадрат модуля ВКФ будет определяться как
2
1
0
,1
2
1
0
,1
2
,
)(2
exp
)(2
exp)(
L
i
i
L
i
tiklp
L
ilk
ja
L
ilk
jamR
,
что представляет собой
)( lk
–ю компоненту ДПФ энергетического спектра последова-
тельности
}{
,1 i
a
. Поскольку энергетический спектр
}{
,1 i
a
есть ДПФ от ее периодической
АКФ, а последняя равняется –1 при всех значениях аргумента кроме нуля, где она равня-

232
ется
L
, получаем
1
0
1
0
11,
2
,
)(2
exp1
)(2
exp)()(
L
m
L
m
pklp
L
mlk
jL
L
mlk
jmRmR
.
Последняя сумма отличается от нуля и равна L только при
lk
, так что, учитывая все по-
лученные результаты и перейдя к нормированным корреляциям, получаем
.mod0,,
1
,mod0,,0
,mod0,,
1
,mod0,,1
)(
2
2
,
Lmlk
L
L
Lmlk
Lmlk
L
Lmlk
m
klp
Откуда видно, что квадрат корреляционного пика ансамбля (7.48)
L
L
L 11
2
2
max
,
т.е. практически совпадает с границей Велча (7.45). Таким образом, рассматриваемый ан-
самбль является минимаксным, оптимальным образом реализуя асинхронный вариант
CDMA.
Описание вышеприведенного ансамбля можно найти, например, в [71], а еще ранее
и независимо он был использован в глобальной спутниковой навигационной системе
ГЛОНАСС (см. параграф 11.1) Одним из достоинств данного множества сигнатур в срав-
нении с другими многофазными ансамблями является возможность формирования сигна-
тур простым сдвигом несущей частоты. Действительно, увеличение несущей частоты
0
f
на
Lk /)1(
эквивалентно линейному приращению фазы между соседними чипами на
величину
Lk /)1(2
, что в точности совпадает с предписанным правилом (7.48).
Несмотря на наличие множества других минимаксных многофазных ансамблей,
бинарные
}1{
семейства традиционно считаются более привлекательными с реализаци-
онной точки зрения, и остальная часть параграфа будет посвящена некоторым важным
примерам множеств бинарных сигнатур.
7.5.2. Множества Голда.
Следующие свойства бинарных
}1{
m–последовательностей служат объяснением
метода построения множества, найденного Голдом.
1. Если бинарную m–последовательность
}{
i
u
периода
12
n
L
подвергнуть опе-
рации децимирования с индексом децимации
d
, где
d
взаимно простое с
L
, то результи-
рующая последовательность
}{
i
v
снова окажется бинарной m–последовательностью тако-
го же периода. Операция децимирования означает выбор каждого
d
–го символа последо-
вательности
}{
i
u
и запись полученных таким образом элементов друг за другом, так что
dii
uv
. Назовем полученную в результате указанной процедуры последовательность
}{
i
v
децимацией последовательности
}{
i
u
.
2. Пусть память
n
бинарной m–последовательности
}{
i
u
является нечетным чис-
лом, а индекс децимации
12
s
d
, где
s
взаимно просто с
n
. Тогда
d
взаимно простое
число с длиной
12
n
L
последовательности
}{
i
u
, децимированная последовательность
}{
i
v
является
m
–последовательностью того же периода
L
, а ненормированная периоди-
ческая ВКФ
)(
,
mR
uvp
последовательностей
}{
i
u
и
}{
i
v
принимает только три следующих
значения:

233
1,,1,0},1,12{1,1)1(2)(
2
1
,
LmLmR
n
uvp
. (7.50)
3. Пусть память
n
бинарной m–последовательности
}{
i
u
является четным числом,
но не кратно четырем, а индекс децимации
12
s
d
, где s – четное и взаимно простое с
2/n
. Тогда d взаимно просто с длиной
12
n
L
последовательности
}{
i
u
, децимирован-
ная последовательность
}{
i
v
является
m
–последовательностью того же периода
L
, а не-
нормированная периодическая ВКФ
)(
,
mR
uvp
последовательностей
}{
i
u
и
}{
i
v
принима-
ет только три следующих значения:
1,,1,0},1,12{1,1)1(2)(
2
2
,
LmLmR
n
uvp
. (7.51)
Доказательство этих утверждений достаточно сложно и требует более глубоких
знаний об алгебре расширенных конечных полей. Оставляем их доказательство в стороне
и отсылаем заинтересованного читателя к оригинальной статье Голда [72] или другим ис-
точникам [например, 9, 70].
Возьмем теперь пару
m
– последовательностей:
}{
i
u
и ее децимацию
}{
i
v
, удовле-
творяющую вышеприведенным условиям 2 или 3, и сформируем ансамбль из K сигнатур
по следующему правилу
,
,
,,,2,1,
,2
,1
,
iiL
iiL
kiiik
va
ua
Lkvua
(7.52)
где
,1,0,1,i
. Другими словами, строим
L
сигнатур путем посимвольного умноже-
ния
}{
i
u
на циклические копии
}{
i
v
, а еще две сигнатуры образуют непосредственно сами
исходные
m
– последовательности. В итоге имеем всего
122
n
LK
сигнатур. На
практике традиционно бинарные
}1{
m
– последовательности формируются как двоич-
ные
}1,0{
последовательности, т.е. над полем
)2(GF
с помощью линейного регистра
сдвига, с последующим отображением элементов
)2(GF
на вещественную пару
}1{
(см.
параграфы 6.6, 6.7). Таким образом, реализация соотношений (7.52) может быть осущест-
влена с помощью двух
n
–разрядных LFSR, генерирующих
}1,0{
последовательности
}{
i
u
и
}{
i
v
, предшественников
}{
i
u
и
}{
i
v
. Действительно, вместо умножения
}{
i
u
на
}{
ki
v
может быть реализована операция сложения по модулю 2 их предшественников с после-
дующим отображением результата на множество
}1{
:
kii
vu
kii
vu
)1(
. Рис. 7.18 ил-
LFSR
памяти n
LFSR
памяти n
+
2mod
Задержка
на k тактов
Отображение
на {±1}
Отображение
на {±1}
Отображение
на {±1}
}{
,1 iL
a
}{
,2 iL
a
}{
i
u
}{
i
v
Lka
ik
1},{
,
Рис.7.18. Генерирование последовательностей Голда.
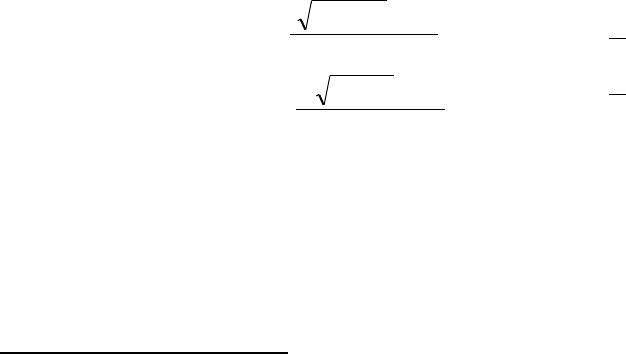
234
люстрирует практическую реализацию алгоритма Голда в соответствие с вышеприведен-
ным обсуждением.
Оценим корреляционный пик ансамбля Голда, начав с вычисления корреляций
первых
L
последовательностей
1
0
1
0
,,,
)(
L
i
mlikimii
L
i
milikklp
vvuuaamR
.
Очевидно, что поскольку случай
Lm mod0
и
lk
отвечает основному лепестку АКФ
k
–й сигнатуры, то следует анализировать ситуацию, когда приведенные равенства одно-
временно не выполняются. Однако, тогда либо
mii
uu
, либо
mliki
vv
представляют со-
бой некоторые другие сдвиги исходных последовательностей
}{
i
u
,
}{
i
v
, либо только одно
из этих произведений есть последовательность, состоящая из одних единиц. В первом
случае имеем ВКФ исходных
m
– последовательностей
}{
i
u
,
}{
i
v
, принимающую только
три значения, указанных в (7.50) или (7.51), тогда как во втором – боковые лепестки не-
нормированной АКФ одной из последовательностей
}{
i
u
,
}{
i
v
, т.е. –1.
Рассмотрим теперь ВКФ последовательностей
Lka
ik
,,2,1},{
,
и
1},{
,
Lla
il
:
1
0
,
)(
L
i
kimiiklp
vuumR
.
Если
Lm mod0
, то
1
mii
uu
, и величина ВКФ есть просто постоянная составляющая
}{
i
v
, т.е. –1. В противном случае,
simii
uuu
при некотором s, и имеем ВКФ исходных
m
– последовательностей, подчиняющуюся ограничениям (7.50) или (7.51). Аналогичный
результат имеет место для ВКФ последовательностей
Lka
ik
,,2,1},{
,
и
2},{
,
Lla
il
.
Наконец ВКФ
}{
,1 iL
a
и
}{
,2 iL
a
непосредственно представляет собой ВКФ ис-
ходных
m
– последовательностей, тогда как их автокорреляционные функции, как АКФ
m
– последовательностей, обладают боковыми лепестками ненормированной АКФ, рав-
ными –1. Учитывая совместно все полученные результаты, видно, что корреляционный
пик (7.44) множества Голда определяется максимальным по модулю значением ВКФ, ус-
танавливаемым соотношениями (7.50) или (7.51). После нормировки к длине L приходим
к следующей оценке
,4mod2,
4
,2mod0,
2
4mod2,
11)(L2
,2mod0,
1)1(2
2
2
2
2
2
max
n
L
n
L
n
L
n
L
L
(7.53)
с последним приближением, отвечающим большой длине
1L
. Как видно, при любом
нечетном значении памяти n ансамбли сигнатур Голда асимптотически
)1( L
удовле-
творяют нижней границе Сидельникова (7.46), тогда как при четном n, не кратном четы-
рем, их проигрыш в уровне
max
по отношению к граничному составляет порядка 3 дБ.
1
Пример 7.5.1. Построим последовательности Голда длины
712
3
L
. Ансамбль
такой малой длины не имеет практического значения, однако служит хорошей иллюстра-
1
При
4mod0n
также существует ансамбль Голда с тем же значением корреляционного пика, как и в
случае
4mod2n
, но с числом последовательностей на одну меньше [67, 70].

235
цией идеи построения. Начнем с бинарной
}1,0{
m– последовательности, впервые встре-
тившейся в примере 6.6.1:
}1,1,0,1,0,0,1{}{
i
u
. Индекс децимации
3d
удовлетворяет
вышеприведенному ограничению в пункте 2. Тогда децимированная последовательность
}0,0,1,0,1,1,1{}{
i
v
. Посимвольное суммирование
}{
i
u
и
}{
i
v
по модулю два дает после-
довательность
}1,1,1,1,1,1,0{
, которая после отображения на алфавит
}1{
дает первую по-
следовательность Голда
}{}{
,1
i
a
. Сдвиг
}{
i
v
вправо на одну позицию и сло-
жение по модулю 2 с
}{
i
u
дает последовательность
}1,0,0,0,1,1,1{
, которая после перехода
к символам
}1{
дает вторую последовательность Голда
}{
. Еще шесть после-
довательностей Голда получаются в результате дальнейших сдвигов
}{
i
v
, сложения по
модулю 2 с
}{
i
u
и изменения символов на
}1{
. Совместно с
}{
i
u
и
}{
i
v
, преобразован-
ных в
}1{
последовательности, получаем всего
912
3
K
последовательностей. Про-
верка значения пика корреляции в данном простейшем случае не имеет особого значения,
поскольку при
7L
ненормированная периодическая корреляция не может превосходить
значения 5, предсказываемого соотношением (7.53). Построения ансамблей Голда боль-
ших длин и проверка их оптимальности является предметом задачи 7.40.
Ансамбли Голда пользуются большой популярностью в современных CDMA сис-
темах. Достаточно сказать, что они используются в глобальной спутниковой навигацион-
ной системе GPS NAVSTAR для разделения сигналов спутников, в системе мобильной
связи 3-го поколения стандарта UMTS для скремблирования CDMA кодов и т.п.
7.5.3. Множества Касами и их расширения.
Принцип построения множеств Касами очень близок к описанной выше схеме кон-
струирования последовательностей Голда. Осуществим операцию децимирования над би-
нарной
}1{
m– последовательностью
}{
i
u
четной памяти
hn 2
с индексом децимации
12
h
d
. Очевидно, что d не взаимно простое число с периодом
)12)(12(12
hhn
L
последовательности
}{
i
u
, что приводит к децимированной по-
следовательности
}{}{
dii
uv
с периодом, являющимся множителем L. Можно показать,
что если
}{
i
u
инициализирована так, что
1
0
u
, то «короткая» последовательность
}{
i
v
будет бинарной m– последовательностью периода
12
1
h
L
, ненормированная периоди-
ческая ВКФ которой с
}{
i
u
на периоде L принимает только два значения [9,70,73]:
1,,1,0,1112)(
,
LmLmR
h
uvp
. (7.54)
Тогда
1
L
сигнатур Касами длины L образуются путем посимвольного произведения ис-
ходной m– последовательности
}{
i
u
с
1
L
различными циклическими копиями
}{
i
v
, а еще
одной сигнатурой является сама «длинная» последовательность, так что:
.
,,,2,1,
,1
1,
1
iiL
kiiik
ua
Lkvua
(7.55)
где
,1,0,1,i
. Таким образом, всего имеется
121
1
LLK
h
подобных сиг-
натур периода L. Очевидно, что снова умножение
}1{
последовательностей
}{
i
u
,
}{
i
v
может быть реализовано как сложение по модулю 2 их
}1,0{
предшественников
}{
i
u
,
}{
i
v
,
но в отличие от множества Голда для формирования «короткой» последовательности
}{
i
v
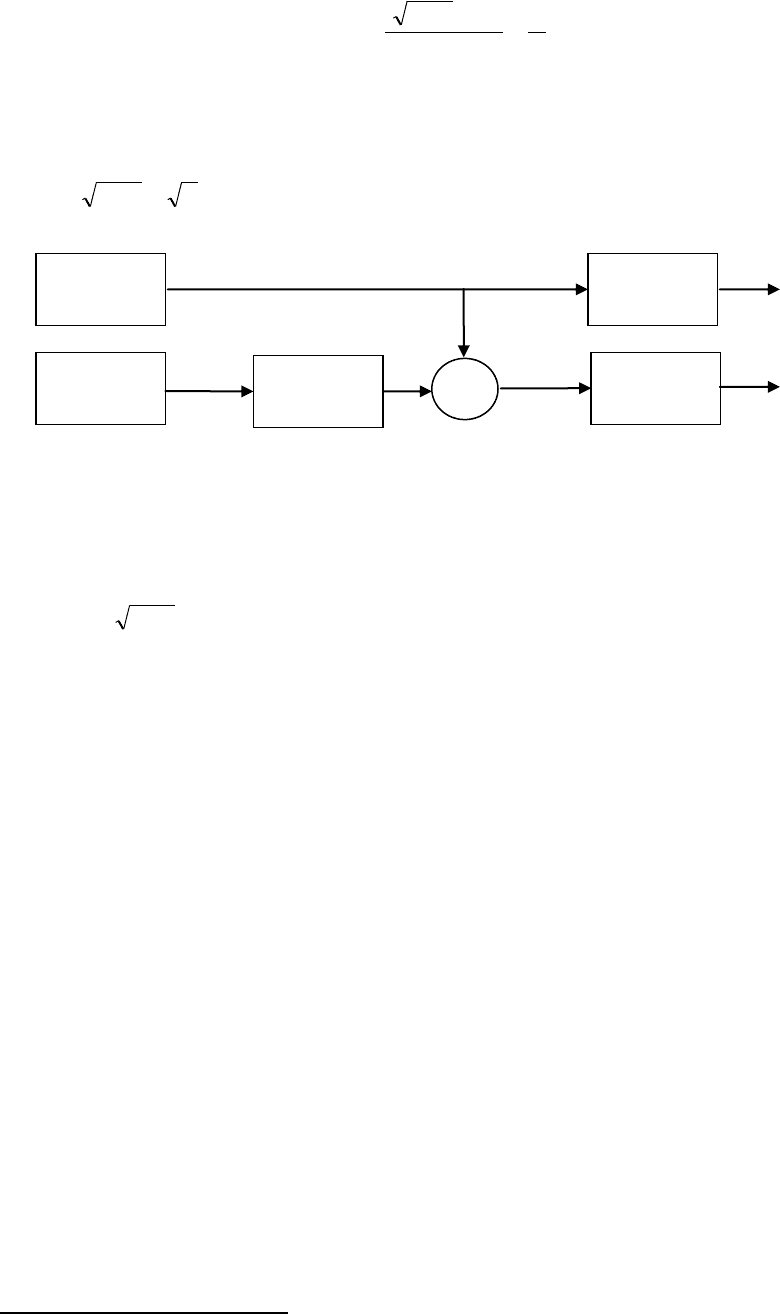
необходим регистр сдвига LFSR в два раза меньшей длины
2/nh
(см. рис. 7.19).
236
Доказательство минимаксных свойств множества Касами
1,
111
2
2
2
max
L
L
L
L
(7.56)
осуществляется на основе (7.54) аналогично доказательству свойств множества Голда и
оставляется читателю в качестве упражнения (задача 7.28). Сравнение двух бинарных ан-
самблей показывает значительный (6 дБ) выигрыш множеств Касами в уровне корреляци-
онного пика у ансамблей Голда одинаковой длины за счет значительно меньшего (в
LLL 1/)2(
раз) числа последовательностей K.
1
Пример 7.5.2. Сконструируем множество Касами длины
12
4
L
)41,2( LKh
. Начнем с построения бинарной
}1,0{
m– последовательности
}{
i
u
длины
1512
4
L
на основе примитивного полинома
1)(
4
xxxf
и начального со-
стояния регистра
0,1
3210
uuuu
. Получаем
}1,1,1,0,1,0,1,1,0,0,1,0,0,0,1{}{
i
u
. Де-
цимирование этой последовательности с индексом
512
h
d
дает m– последователь-
ность периода три
}1,0,1,1,0,1,1,0,1,1,0,1,1,0,1{}{
i
v
. Сумма по модулю 2 последовательно-
сти
}{
i
u
с тремя сдвинутыми копиями
}{
i
v
после перехода к алфавиту
}1{
образует пер-
вые три последовательности Касами:
}{}{
,1
i
a
,
}{}{
,2
i
a
,
}{}{
,3
i
a
.
Четвертым представителем является
}{
i
u
, символы который преобразованы во множество
}1{
:
}{}{
,4
i
a
. Непосредственное вычисление показывает, что
все их ненормированные ВКФ, также как и боковые лепестки ненормированных АКФ
первых трех последовательностей принимают только значения вида –5 и 3, так что
9/1
2
max
в полном соответствии с (7.56). Построение произвольных множеств Касами и
проверка их корреляционных свойств на языке программирования Matlab является пред-
метом задачи 7.41.
Относительно малое число последовательностей Касами подчеркивает важность
способа, позволяющего расширить множество Касами почти в два раза без изменения ве-
личины корреляционного пика, который был предложен Камалетдиновым [74]. Пусть n
1
Для бинарных множеств границы (7.45), (7.46) могут быть незначительно улучшены, если учесть, что не-
нормированные корреляции принимаю только целые значения. В результате оказывается, что как множества
Голда с нечетной памятью, так и множества Касами строго (а не только асимптотически) оптимальны по
уровню корреляционного пика среди всех бинарных множеств [67, 70].
LFSR
памяти n
LFSR
памяти n/2
+
2mod
Задержка на
k тактов
Отображе-
ние на {±1}
Отображе-
ние на {±1}
}{
,1
1
iL
a
}{
i
u
}{
i
v
1,
1},{ Lka
ik
Рис.7.19 Формирование последовательностей Касами.
237
кратно 4, т.е.
rn 4
, где r – целое, так что
,4095,255,1511612
4
rr
L
. Тогда при
данных параметрах в дополнение к множеству Касами существует и другой бинарный ан-
самбль длины L и объема
1L
, называемый ансамблем бент–последовательностей [9,
75], который обладает тем же минимаксным свойством
LLL /1/)11(
222
max
. В
самых общих выражениях построение бент–последовательностей снова состоит в посим-
вольном умножении двух исходных последовательностей: «длинной» m– последователь-
ности периода
12
4
r
L
и некоторой специальной последовательности, основанной на
т.н. бент–функциях. Детали построения указанных последовательностей достаточно
сложны и здесь могут быть опущены, однако основным является тот факт, что значение
нормированной ВКФ любой бент–последовательности с любой из первых
1
L
последова-
тельностей Касами (7.55) не превосходит по модулю корреляционный пик как ансамбля
Касами, так и бент–последовательностей. Следовательно, возможно образовать составной
ансамбль, включающий
111212
2
1
LL
rh
последовательностей Касами и
1L
бент–последовательностей и обладающий прежним значением корреляционного
пика
LLL /1/)1(
22
max
. Полученный таким образом ансамбль является уникальным
в том смысле, что среди всех известных бинарных ансамблей со значением корреляцион-
ного пика
L/1
2
max
только он один обладает наибольшим числом сигнатур
112 LK
.
7.5.4. Ансамбли Камалетдинова.
Существуют и другие бинарные минимаксные ансамбли [9, 67], отличающиеся от
рассмотренных только тонкой структурой последовательностей, но не значениями длины
L, объема K и корреляционного максимума
max
. На этом фоне особый интерес представ-
ляют ансамбли, описанные Камалетдиновым [76], поскольку охватывают диапазон длин,
отличный от установленных для множеств Голда и Касами.
Для более ясного восприятия идеи рассмотрим отчасти упрощенную версию мно-
жеств Камалетдинова, не приводящую, тем не менее, к потерям как в диапазоне охвата
длин, так и достижимых значений параметров. Для обрисования в общих чертах первой
схемы Камалетдинова возьмем простое нечетное
3p
вида
4mod334 hp
и распро-
страним определение двузначного характера
)(x
, данное в параграфе 6.8, на нулевой
элемент
)(pGF
, полагая
1)0(
(альтернативный вариант
1)0(
приводит к анало-
гичному результату). Будем трактовать позицию символа последовательности с номером i
как элемент поля
)(pGF
, т.е. приведенным по модулю p, и образуем
1p
p–ичных по-
следовательностей
ik
d
,
над
)(pGF
(т.е. с элементами из этого поля) по правилу:
,1,
,,
,1,,2,1,
,
pki
pki
pki
d
i
i
iki
ik
(7.57)
где все арифметические операции осуществляются по правилам конечных полей,
–
примитивный элемент
)(pGF
и
,1,0,1,i
. Можно заметить, что каждая последова-
тельность в (7.57) образована как сумма последовательностей с взаимно простыми перио-
дами p и p–1
)1(
01
p
и, следовательно, обладает периодом
)1( ppL
. Осущест-
вим теперь отображение последовательностей (7.57) на бинарный алфавит
}1{
, исполь-
