Ипатов В.П. Широкополосные сигналы

Подождите немного. Документ загружается.

208

ми частотами

ff 

ff 

. Если нижняя несущая частота

ff 

превосходит полосу

произведения

)()(

tUtU



, то после отфильтровывания слагаемого с более высокой часто-

той оставшийся полосный сигнал с более низкой частотой будет обладать комплексной

огибающей вида

)()(

tUtU



, т.е. в точности произведением, получаемым после снятия

расширения. Аналогичным образом, слагаемое с более высокой частотой представляет со-

бой полосный сигнал, комплексная огибающая которого является аналогичным произве-

дением, но без комплексного сопряжения.

Прямое расширение используется во всех CDMA стандартах 2-го и 3-го поколений:

IS-95 (cdmaOne), UMTS и cdma2000. В них используются различные комбинации алфави-

тов манипулированных данных и сигнатур, которые более подробно будут рассмотрены в

параграфе 11.2.

7.1.3. Расширение спектра прыгающей частотой.

При расширении спектра с помощью прыгающей частоты (frequency hopping (FH))

используются ЧМ сигнатуры, а модуляция данных, как правило, также осуществляется с

помощью ЧМ. Традиционно различают два типа расширения прыгающей частотой: бы-

строе (fast) и медленное (slow), критерием классификации которой служит соотношение

между длительностями чипа



и символа данных

. Для быстрой FH

lT /

, где

1l

–

натуральное число, тогда как для медленной FH

lT

, где

1l

– натуральное. Другими

словами, при быстрой FH на один символ данных приходится несколько скачков частоты,

тогда как при медленной FH в течение одного частотного скачка сигнатуры могут быть

переданы несколько символов данных. Для лучшего понимания сущности этого типа рас-

ширения обратимся к примеру.

Пример 7.1.1. Возьмем ЧМ сигнатуру примера 5.5.1 и используем ее для расшире-

ния спектра с помощью быстрой FH в комбинации с бинарной модуляцией данных. В

этом случае число различных частот в сигнатуре

5M

, длина сигнатуры

8N

, а один

символ данных передает один бит информации, так что

TT 

. Предположим, что в схеме

быстрой FH

8 Nl

, т.е. на один бит данных приходится 8 скачков частоты. Тогда пол-

ная последовательность ЧМ чипов, представленная на рис. 5.3, передается в течение одно-

го бита. Если бит данных равен нулю, то частотный образец излучается на несущей часто-

те, равной

, тогда как для бита, равного единице, несущая частота изменяется на

Очевидно, что разность между частотами

должна быть не меньше полосы, зани-

маемой сигнатурой, т.е.

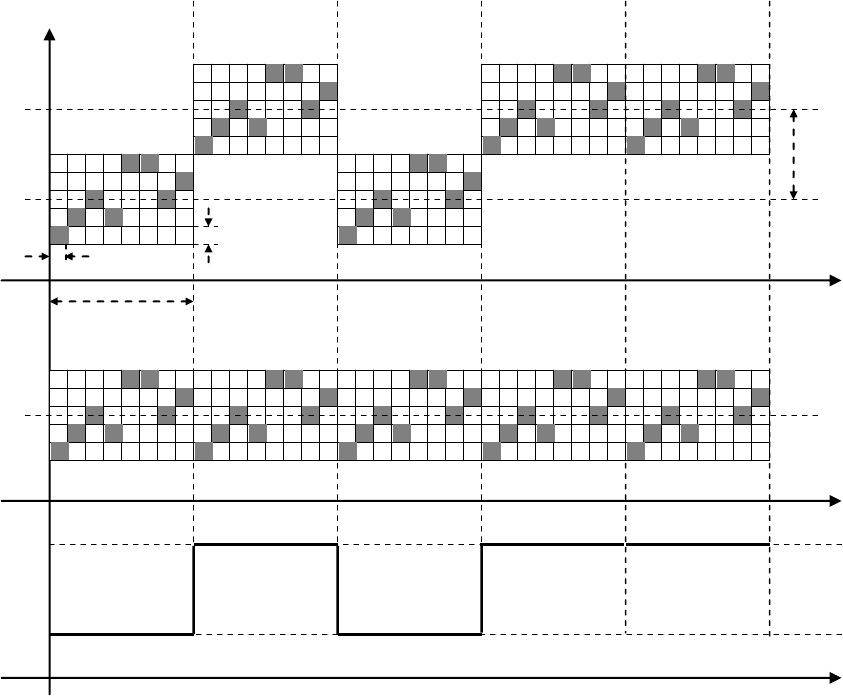
. На рис. 7.11, а изображен передаваемый частотный образец,

соответствующий потоку битовых данных вида

01011

. Как можно видеть, спектр одиноч-

ного бита данных, полоса которого перед расширением была примерно

T/1

, расширяется

до полосы, равной

TMNMMF // 

, т.е. становится в

раз шире (см. параграф

5.6).

На приемной стороне снятие расширения заключается в обратном преобразовании

наблюдаемого колебания на промежуточную частоту

. С этой целью используется

опорное колебание несущей частоты

ff 

, модулированное согласно ЧМ образца сиг-

натуры с необходимой задержкой во времени (рис. 7.11, b). В результате сигнал со снятым

расширением представляет собой обычное узкополосное колебание, частотно-

манипулированное в соответствие с передаваемыми данными, где нулевой бит данных пе-

редается более низкой частотой, чем бит, отвечающий единице. Теперь спектр отдельного

символа данных возвращается к полосе

T/1

и может быть использован обычный бинар-

ный ФМ демодулятор для восстановления принятых данных. 

Следующий пример иллюстрирует алгоритм расширения спектра медленной FH.

209

Пример 7.1.2. Используем ту же самую сигнатуру снова в комбинации бинарной

ФМ данных и приравняем длительности чипа и символа данных:



. Последнее

означает, что текущая частота остается постоянной в течение всей длительности бита дан-

ных, а скачок частоты происходит только при переходе от одного бита к следующему.

Частотный образец сигнатуры растягивается во времени и его длина охватывает

бит

данных (рис. 7.12, а). Предположим, что в течение бита данных с номером

частота сиг-

натуры равна

. Тогда частота передачи становится равной

Ff 

в случае нулевого би-

та данных и

Ff 

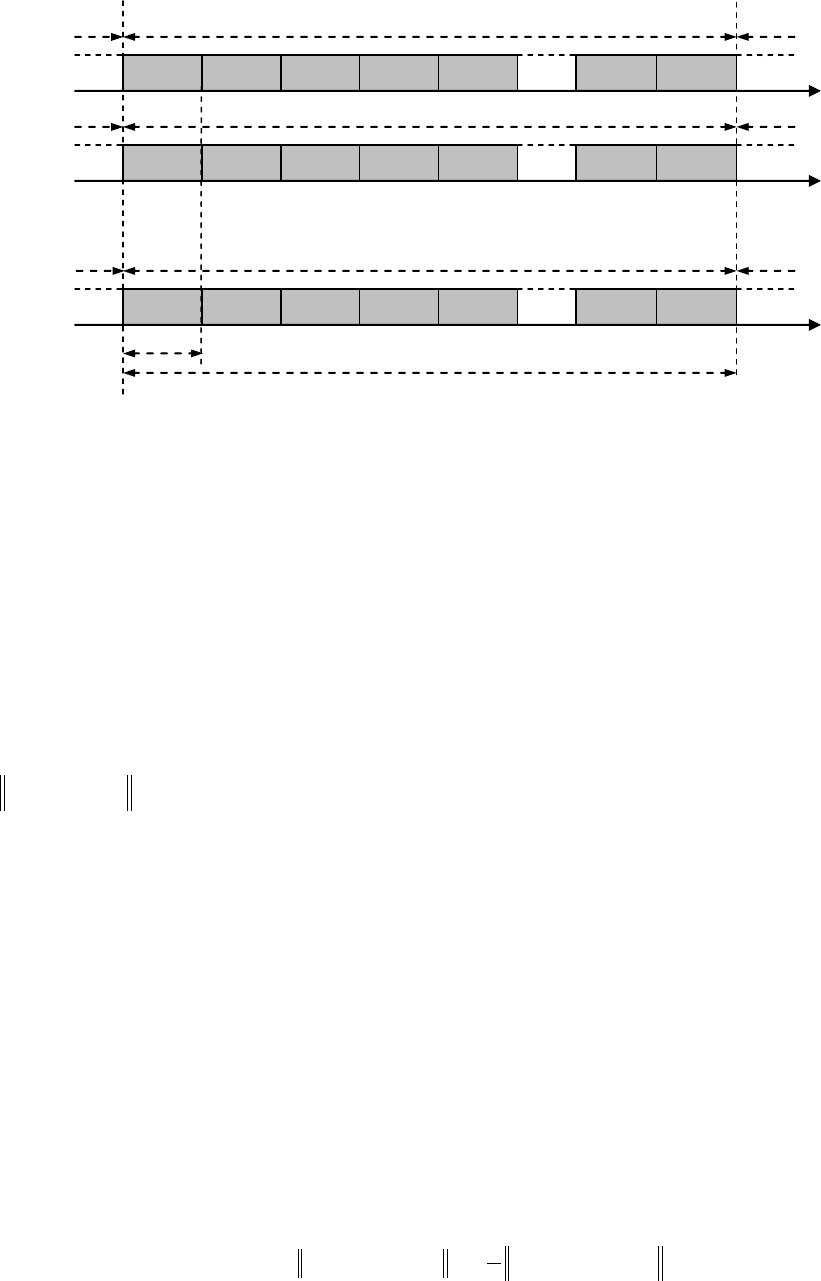
для бита данных, равного единице. Рис. 7.12, b служит иллюстрацией

этого для битового потока

00101101

. Принципиальное отличие между быстрой и медлен-

ной FH теперь очевидно: последняя не расширяет спектр отдельного символа данных,

увеличивая только полосу, занимаемую системой. Это аналогично тому, как если бы сис-

тема просто время от времени переключалась бы с одной рабочей частоты на другую, но

не происходило бы переключения на интервале фиксированной группы символов данных.

На приемной стороне обратное преобразование на промежуточную полосу

выполняет-

ся с помощью опорного сигнала на частоте

ff 

, повторяющего частотный образец

сигнатуры (задержанным во времени соответствующим образом) (рис. 7.12, с). Данная

операция возвращает колебание в полосу, соответствующую простой (без скачков часто-

ты) ЧМ модуляции данных (рис. 7.12, d), так что для восстановления передаваемых дан-

ных может быть использован обычный ЧМ демодулятор (рис. 7.12, с). 

Методы, иллюстрируемые приведенными выше примерами для передачи данных с

MFf



Биты



 NTT

Рис.7.11. Расширение-сужение с помощью быстрой FH (fast FH).

ff 

210

помощью бинарной ФМ, легко обобщаются на случай модуляции данных произвольной

ФМ (см. задачи 7.5-7.7).

Расширение спектра с помощью прыгающей частоты обладает некоторыми осо-

бенностями, делающими этот метод особенно привлекательным для военных приложений,

в частности в различных антагонистических сценариях борьбы против систем подавления

[3, 6]. В то же время, его коммерческое использование до недавнего времени совершенно

незначительно, по крайней мере в отношении FFH. Однако внедрение технологии Blu-

etooth [55] указывает, что этот тип расширения спектра также обладает хорошими ком-

мерческими перспективами.

Биты:

ff 



MFf



Рис.7.12. Расширение-сжатие с помощью медленной FH.

211

7.2. Синтез ансамблей сигнатур для синхронного CDMA с прямым рас-

ширением спектра.

7.2.1. Постановка задачи.

Рассмотрим

–пользовательскую CDMA систему с прямым расширением спектра,

в которой все пользовательские потоки данных и все сигнатуры жестко синхронизованы,

т.е. характеризуются нулевым взаимным временным сдвигом на входе приемника. Как

указывалось в параграфе 4.4, классическим примером подобной системы может служить

канал «вниз» система мобильной радиосвязи с CDMA, в которой базовая станция полно-

стью контролирует временное положение сигналов, адресованных всем пользователям в

пределах соты. Очевидно, что групповой сигнал достигает приемника мобильного або-

нента с сохранением начальной синхронизации между сигналами, адресованными различ-

ным индивидуальным пользователям. В приводимом здесь анализе будем считать, что

имеет место идеализированная модель канала, в котором многолучевая задержка на рас-

пространение

max



меньше периода следования чипов



пользовательских сигнатур или

используется эффективный эквалайзер, исключающий все многолучевые компоненты, за-

держка которых превышает



. Данное предположение позволяет игнорировать любое по-

тенциальное нарушение идеальности синхронизации компонент принятого сигнала.

Согласно концепции прямого расширения спектра, комплексная огибающая приня-

того группового сигнала

),,,;(

21 K

tS bbb 



представляет собой сумму по

комплексных

огибающих сигнатур, манипулированных пользовательскими потоками данных, каждая из

которых определяется соотношением (7.6). В общем случае каждый из пользовательских

сигналов может обладать собственной амплитудой, однако ограничимся простейшим слу-

чаем равной интенсивности сигналов. Поскольку предположение об идеальном синхро-

низме позволяет положить все задержки



и начальные фазы



в (7.6) равными нулю,

получаем





kkK

tStBtS

)()(),,,;(







bbb

. (7.10)

Сосредоточим наше внимание на интервале длительности

одиночного символа

данных. Снова, вследствие полного синхронизма, начало и конец текущих символов дан-

ных всех пользователей строго совпадают. Если через

обозначить

– й текущий поль-

зовательский символ данных, то на одиночном символьном интервале (7.10) может быть

записано в следующем виде





tStbtS

)()();(



, (7.11)

где

),,,(

21 K

bbb b

–

–мерный вектор текущих символов данных всех пользовате-

лей.

Вспомним теперь, что каждая сигнатура в CDMA системе с прямым расширением

является АФМ сигналом, описываемым моделью (5.2):









)()(

itSatS



, (7.12)

где

},,,{

1,1,0, Nkkk

aaa 

– кодовая последовательность, манипулирующая чипы

– й

сигнатуры, а

– коэффициент расширения, т.е. число чипов на один символ данных.

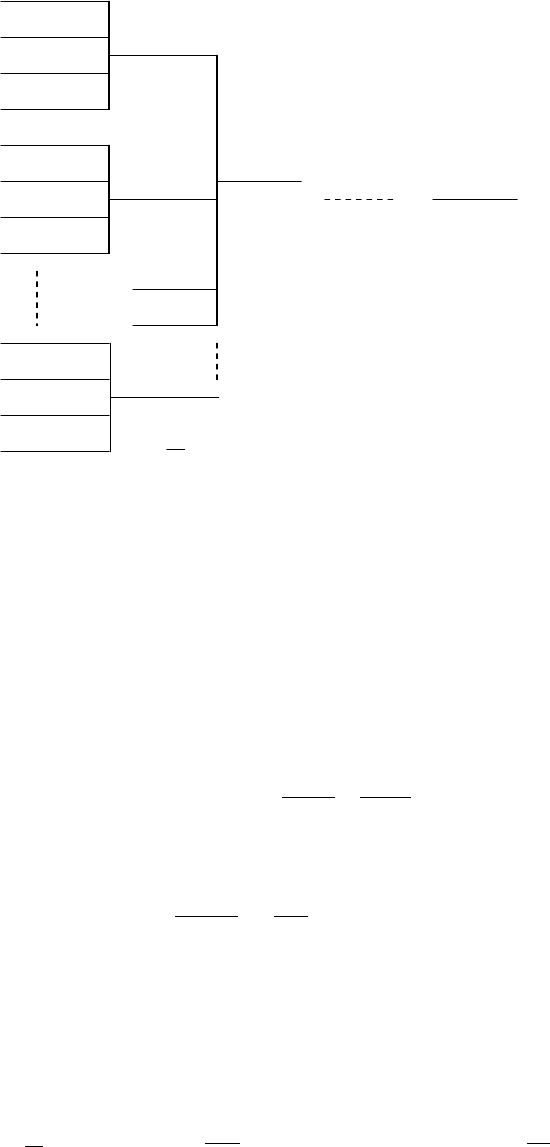
Рис. 7.13 демонстрирует строгое взаимное расположение между чипами сигнатуры и гра-

ницами передаваемых символов данных при синхронном варианте CDMA.

Основываясь на (7.11)–(7.12), можно сформулировать несколько подходов к выбо-

212

ру ансамблей сигнатур для сетей с синхронным CDMA и прямым расширением спектра.

Среди основных факторов, оказывающих влияние на процедуру и результаты оптимиза-

ции множества сигнатур, следует отметить связь между числом пользователей

и пока-

зателем расширения

, а также алгоритмом приема (многопользовательский или обыч-

ный).

7.2.2. Оптимизация множества сигнатур по критерию минимума расстояния.

Предположим, что допустим приемник любой сложности и, следовательно, разре-

шается использовать оптимальный (многопользовательский) алгоритм оценивания векто-

ра данных

, основанный на поиске значения

, минимизирующего расстояние между

наблюдением

)(ty

и претендентом группового сигнала

);( bts

(см. параграф 4.1). В тер-

минах комплексной огибающей последнее означает минимизацию по

квадрата расстоя-

ния

);()( btStY





, где

);( btS



определяется (7.11). Тогда строгое теоретическое обосно-

вание очевидным образом указывает на нахождение ансамбля

сигнатур

})(,),(),({

tStStS







, минимизирующего вероятность ошибки в оценке

–

пользовательского вектора данных

),,,(

21 K

bbb b

. Возвращаясь к материалу парагра-

фа 2.3, вспомним, что асимптотически (т.е. при достаточно большом отношении сигнал-

шум), минимизация вероятности ошибки эквивалентна максимизации минимума расстоя-

ния в созвездии из

передаваемых сигналов. В рассматриваемом случае подлежащие

обсуждению альтернативные сигналы представляют собой копии (7.11), отвечающие раз-

личным векторам данных

. Следовательно, задачу оптимизации множества сигнатур

можно сформулировать как задачу максимизации минимума квадрата расстояния:

max),(min

min













, (7.13)

где минимальное расстояние

min

ищется по всем различным парам векторов данных

),,,(

21 K

bbb b

),,,(

21 K

bbb







b





и, согласно (2.43), определяется как

);();(

);();(),( bbbbbb











tStStstsd



. (7.14)

Рассмотрим подробно передачу бинарных данных, когда символами являются би-

0,1

1,1

2,1

2,1 N

1,1 N

0,2

1,2

2,2

2,2 N

1,2 N

0,K

1,K

2,K

2, NK

1, NK



N

1,1 i

1,2 i

1, iK

1,1 i

1,2 i

1, iK

1-й абонент

2-й абонент

K-й абонент

Рис.7.13. Положение символа данных и чипа в синхронной CDMA.

213

ты, непосредственно передаваемые с помощью бинарной ФМ, так что

Kkbb

,,2,1,1, 



. Подобное сужение диапазона упрощает анализ битов, допуская

непосредственный переход к последующему расширению до произвольной ФМ. Тогда

использование (7.11), (2.41) и (2.42) в (7.14) приводит к следующему результату

 





 





kllkb

EdttStSd

1 1

)(

),(





, (7.15)

где

kkk





принимает одно из трех возможных значений: 0 или 2;





dttSE

)(



– энергия

–й сигнатуры, затрачиваемая для передачи одного бита (бу-

дем полагать, что эти энергии одинаковы для всех

пользователей); и





dttStS

)()(





–

коэффициент корреляции между комплексными огибающими

–й и

– сигнатур. При ис-

пользовании свойств коэффициента корреляции, вытекающих из его определения:

1



lkkl





, соотношение (7.15) принимает вид, ясно свидетельствующий, что расстояние

всегда вещественно:

 



 





1 11

)Re(2),(

kllkb

EEd



. (7.16)

Возьмем два вектора данных (битовых образца)



, отличающихся только одним

элементом, например, первым компонентом. Тогда

2,,,3,2,0

 Kk



и из (7.16)

получаем, что

Ed 4),(





. Поскольку

min

никогда не превосходит значения квадрата

расстояния для некоторой конкретной пары



, то

Ed 4

min



. (7.17)

Данная верхняя граница свидетельствует, что ансамбль сигнатур, для которого

Ed 4

min



, следует считать оптимальным по критерию максимума минимального рас-

стояния (7.13). Одним из достаточных условий достижения границы (7.17) является сла-

бая (weak) ортогональность комплексных огибающих сигнатур:

klkl















,,0

,,1

)Re(



. (7.18)

Причина, по которой комплексные огибающие, удовлетворяющие (7.18), называются сла-

бо ортогональными, становится ясной после сравнения выражений (7.18) и (2.46)

)(

klkl





. Последнее является более жестким и требует, чтобы сигналы

)(),( tsts

комплексными огибающими

)(),( tStS



сохраняли ортогональность при любом взаимном

фазовом сдвиге. В то же время два сигнала, промодулированные

)(tS



)()

exp()( tSjjtS







, т.е. просто квадратурными (сдвинутыми по фазе на

2/

) копиями

одного и того же сигнала, являются ортогональными, однако теряют свойство ортого-

нальности, если их взаимный фазовый сдвиг отличается от

2/

. Следовательно,

)(tS



)(tSj



являются только слабо ортогональными. Конечно, любые ортогональные (в смысле

(2.46)) сигнатуры являются слабо ортогональными, но не наоборот.

Для сигнатур, удовлетворяющих (7.18), соотношение (7.16) приводится к виду

214









),( bb

. По крайней мере, одно из слагаемых в данной сумме не является

нулевым, так что

Ed 4

min



, что совместно с (7.17) дает

Ed 4

min



. Следствием этого

является тот факт, что ансамбль из

слабо ортогональных сигнатур оптимален по крите-

рию минимума расстояния, а, значит, (асимптотически) по вероятности перепутывания

различных пользовательских битовых образцов.

Существует множество способов построения ортогональных (удовлетворяющих

(2.46)) широкополосных сигналов различной длины (коэффициента расширения)

. Од-

ним из примеров являются функции Уолша или, в общем случае, матрицы Адамара, рас-

смотренные в 2.7.3, которые позволяют построить ортогональные бинарные коды. Другим

возможным выбором служат циклически сдвинутые копии любой последовательности с

идеальной периодической АКФ, например, троичной, многофазной, др. (см. параграф

6.11). Любой ансамбль из



ортогональных сигнатур тривиальным образом трансформи-

руется во множество слабо ортогональных сигнатур, состоящее из



сигналов, путем

добавления квадратурных копий каждого из сигналов: факт, неоднократно упоминавший-

ся ранее (см. параграфы 2.5, 4.1).

При любом конкретном выборе ортогональных сигнатур размерность сигнального

пространства жестко ограничивает их число (а, значит, и число пользователей

) (см. па-

раграф 2.5). Согласно соотношению (7.12), при заданной форме чипа

–мерный вектор

),,,(

1,1,0, 



Nkkkk

aaa a

–й кодовой последовательности полностью определяет

–ю

сигнатуру, и ортогональность

–й и

–й сигнатур эквивалентна ортогональности векто-

ров

aa ,

. Действительно, повторение вывода (2.52) для комплексных огибающих (аль-

тернативно использованию (5.7)) позволяет записать скалярное произведение

)(),( tStS



как

),(22),(

,,0 lk

iliklk

EaaE aaSS 









, (7.19)

подтверждая тем самым, что ортогональность векторов

aa ,

является необходимым и

достаточным условием ортогональности

)(),( tStS



. Размерность

пространства векто-

ров

кодовых последовательностей явным образом определяет максимальное число



ортогональных сигнатур

)(tS



. Еще раз подчеркнем, что если допустимо квадратурное

расщепление каждой сигнатуры, то максимальное число пользователей, размещаемое в

рамках ансамбля сигнатур, определяется как

NKK 22 





. Однако, если по каким-либо

причинам точный фазовый сдвиг

2/

между квадратурными копиями сигнатур не мо-

жет быть поддержан, то слабой ортогональности не достаточно, и максимальное число

пользователей будет в два раза меньше:

NKK 





Отметим, что слабая ортогональность является только достаточным, но не необхо-

димым условием равенства в (7.17), и, в частности, особенно интересен вопрос о возмож-

ности достижения верхней границы (7.17) при числе сигнатур, превышающем размер-

ность сигнального пространства

. Как следует из предшествующего обсуждения, значе-

ние

равняется либо

, либо

в зависимости от допустимости или нет квадратурно-

го расщепления сигнатур. Синхронные CDMA системы, в которых

nK 

, называются

перенасыщенными (oversaturated), подчеркивая, что избыточное число вовлеченных кодо-

вых векторов исключает вероятность их ортогональности (возможно слабой).

Возможность и алгоритм достижения минимального расстояния, равного верхнему

пределу в (7.17) в перенасыщенных системах были доказаны в [56]. Для более прозрачно-

го обсуждения данной идеи и упрощения используемого обозначения первоначально от-

вергнем возможность удвоения размерности сигнального пространства за счет квадратур-

215

ного расщепления, полагая



. Возьмем

ортонормированных

–мерных векторов

,,2,1, a

, таких, что

kllk

),( aa

, и прибавим к ним еще один вектор, образован-

ный как









. (7.20)

Использование полученных таким образом

1N

векторов

1,,2,1,  Nk

a

для

формирования согласно (7.12)

1 NK

сигнатур означает образование

)1( N

–й сигна-

туры в виде









)(



и, модулируя все сигнатуры бинарными символами данных

1

, получаем групповой

сигнал как































kNk

tSb

btSb

tSbtSbtS

)(

)()();(



. (7.21)

Разность между двумя версиями группового сигнала, отвечающим двум битовым образ-

цам

),,,(),,,,(

121121 









bbbbbb  bb

, составит

2,0,)(

);();(





























 kkk

kNk

bbtS

tStS



Используя тот же подход, что и при выводе (7.15), и ортогональность первых

сигнатур,

приходим к выражению



























Nkb

EtStSd

);();(),( bbbb



. (7.22)

Поскольку битовые образцы различны, то, по крайней мере, одна из величин

1,,2,1,  Nk



отлична от нуля, т.е. равняется

2

. Если



N

, то таковой являет-

ся



одна из множества

 ,,,



, и тогда

Ed 4),(





. Если же



N

, то сла-

гаемые в (7.22) с

0

равны

N/4

, тогда как все остальные будут

NN /)1(4



, при-

водя к

 

















1,1min4),( NEd

. Учитывая полученные результаты, приходим к

следующей нижней оценке минимума квадрата расстояния

 































.4,4

,4,14

14,4min

min

NEN

ENEd

Сравнение полученного результата с (7.17) показывает возможность добавления

еще одной сигнатуры к

ортогональным без изменения минимального расстояния при

4N

. Обобщение этой идеи лежит в основе следующей процедуры построения опти-

мального перенасыщенного ансамбля сигнатур [56-57]. Пусть вектора

,,,

N

aaa 

об-

разуют ортонормированный базис

–мерного пространства, где

,4

–натуральное

число. Используем их в качестве кодов

первичных сигнатур. Организуем перенасыще-

ние дополнительными сигнатурами как результат применения

–этапной (слойной) про-

цедуры. Кодовыми последовательностями дополнительных сигнатур

–го слоя будут

,,2,1,1

,,1,0,

 















aaa

. (7.23)

Иными словами, первый слой дополнительных сигнатур формируется путем расщепления

216

базового множества

 

,,,

N

aaa 

на

l

групп, каждая из которых содержит по че-

тыре исходные сигнатуры. Линейная комбинация (7.20) (при

4N

) этих четырех базис-

ных сигнатур добавляется к своей группе, образуя в общем случае

4/NN 

сигнатур. На

втором этапе (уровне) аналогичным образом делим на группы по четыре все дополни-

тельные сигнатуры первого слоя и снова вводим в каждую группу линейную комбинацию

(7.20) и т.д. Дерево на рис. 7.14 служит иллюстрацией к данной процедуре. Тогда на пер-

вом этапе образуется

l

дополнительных сигнатур, на втором этапе –

l

, и на произ-

вольном

–м шаге –

sl

, что в общем случае составит

1444













дополнительных сигнатур, а с учетом первоначальных, отождествленных с нулевым сло-

ем, общее число сигнатур составит



















14 NN

Поскольку нормы всех векторов (7.23) остаются равными единице, то дополнительные

сигнатуры сохраняют прежнее значение энергии на бит

, что и исходные.

Пусть

)(tS



являются комплексной огибающей

–й сигнатуры из

– го слоя

и пользовательским потоком бит, передаваемых этой сигнатурой. Тогда образование

группового сигнала, аналогичного (7.21), приводит к выражению

 

























tSbtSbtSbtSbtSbtS

)()()()()();(







которое после подстановки (7.23) обращается в

4N

3N

2N

1N



Рис.7.14. Конструирование множества перенасыщенных сигнатур.

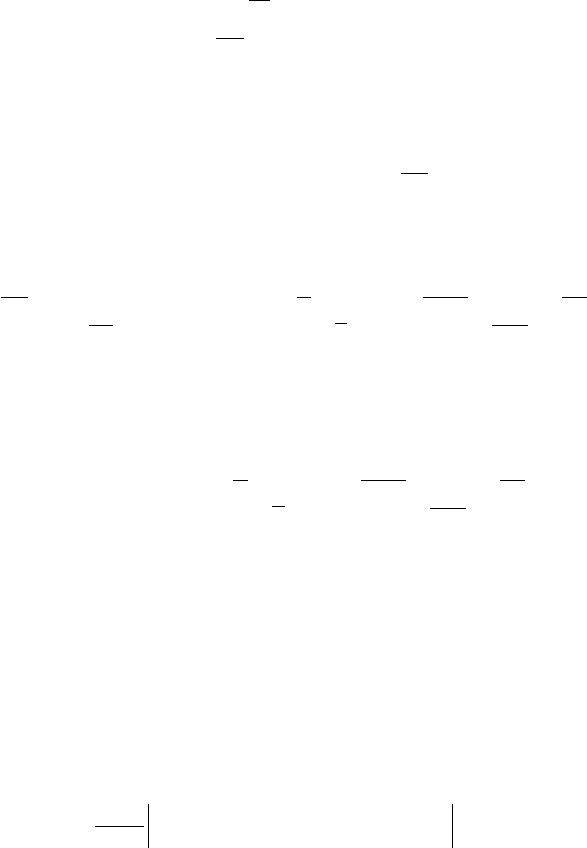
217

  















k m

tSbtS

)(

);(



Двойная сумма по

mk,

в последнем выражении содержит

слагаемых независимо от

значения

. Следовательно, возможно преобразование их в одиночную сумму после из-

менения индекса суммирования как















knmk

, приводящего (при переобо-

значении

kn 

) к виду

 



































































)(

);(

tSbbbbtSbtS







Тогда квадрат расстояния между групповыми сигналами, отвечающими различным бито-

вым образцам, обобщает (7.22) как

),(





















































Ed bb

, (7.24)

где, как и раньше,

2;0 

– разность значений бит, передаваемых сигнатурой

)(tS



пользовательских битовых образцах



. Если все

0,  s

нулевые (биты образцов



во всех дополнительных сигнатур одинаковы), тогда, по меньшей мере, одно из



равно

2

Ed 4),(





. Если

– максимальное число слоев, для которых

0,2  u

, то тогда слагаемые в (7.24), содержащие



, могут быть представлены в

виде

 

1222





xxx 

где

1,,1,0,1,02/  usx



. Число, содержащееся в круглых скобках под знаком

модуля, всегда четно, так что квадрат модуля никогда не меньше единицы. Поскольку в

(7.24) входит ровно

членов, содержащих



при любом фиксированном

, приходим

к оценке

EEd 44/4),(







, доказывающее, что перенасыщенный ансамбль по-

добного сорта не уменьшает минимальное расстояние первичного ортогонального множе-

ства.

В своей общей форме описанная процедура не гарантирует, что дополнительные

кодовые последовательности (7.23), получаемые из первичных бинарных последователь-

ностей, также будут бинарными. Для выполнения указанного требования может быть ис-

пользована версия алгоритма, предложенная в [57], в которой первичные последователь-

ности формируются как строки

-й кронекеровской степени матрицы Адамара 4-го по-

рядка, содержащей нечетное число +1 в любом столбце.

Пример 7.2.1. Построим перенасыщенный ансамбль бинарных сигнатур длины

416 N

. Согласно только что рассмотренной схеме, к

16N

первичным ортогональ-

ным сигнатурам можно добавить пять дополнительных (четыре из первого слоя

1s

одну из второго слоя

2s

), обеспечив общее число пользователей

21K

. Для построе-

ния только бинарных сигнатур воспользуемся матрицей Адамара вида