Ипатов В.П. Широкополосные сигналы

Подождите немного. Документ загружается.

188

элементов

110

,,,

n

ccc 

полностью определяют выходную последовательность, и

ста-

новится циклической сверткой

Nibac

llii

,,1,0,











, (6.36)

где вычитание в индексе осуществляется по модулю

Предъявим к фильтру следующие требования

1,,2,1,0,0

 Nicс



, (6.37)

физический смысл которых состоит в том, что выходной сигнал фильтра имеет ненулевой

основной лепесток, повторяющийся с периодом

N

, тогда как все боковые лепестки ме-

жду ними равны нулю. Подобный фильтр, называемый в дальнейшем фильтром подавле-

ния боковых лепестков (ФПБЛ) (sidelobe suppression filter (SLSF)), имитирует своим от-

кликом идеальную периодическую АКФ. Поскольку для бинарных кодов идеальная АКФ

не достижима (за исключением единственного тривиального сигнала), то ФПБЛ является

рассогласованным и, следовательно, уступает согласованному фильтру в отношении сиг-

нал–шум.

Кратчайшим путем получения точного выражения для коэффициентов фильтра

служит применение дискретного преобразования Фурье (ДПФ). Последовательность

1,,1,0,  Nia



и ее компоненты ДПФ спектра

1,,1,0,

 Nka



связаны друг с дру-

гом прямым и обратным ДПФ:













































1,,1,0,,

exp

Nki

jaa 

Нашей целью является достижение дискретной дельта–функции (6.37) на выходе фильтра,

имеющей только один ненулевой элемент на периоде. Спектр подобной функции является

равномерным:

1,,1,0,

 Nkcc



. Тогда вследствие теоремы о свертке [1] спектр по-

следовательности (6.36) на выходе фильтра может быть представлен в виде

1,1,0,

 Nkcbac

kkk



, где спектр последовательности коэффициентов фильтра

есть ничто иное, как передаточная функция ФПБЛ:

1,,1,0,

 Nk



. (6.38)

Как видно, передаточная функция ФПБЛ обратно пропорциональна спектру сигнала, что

послужило причиной присвоения фильтрам этого типа названия инверсных фильтров. Ин-

версный фильтр как раз и выравнивает входной спектр. Как показывает последнее соот-

ношение, ФПБЛ физически реализуем для любой периодической последовательности,

ДПФ спектр которой не имеет нулевых компонент. Применение обратного преобразова-

ния Фурье к (6.38) дает точное выражение для коэффициентов ФПБЛ

























1,,1,0,

exp

b 

. (6.39)

6.12.2. Вычисление потерь в отношении сигнал шум.

В случае согласованного фильтра (см. рис.6.20) его коэффициентами будут слу-

жить (игнорируя несущественный общий множитель) значения символов зеркально ото-

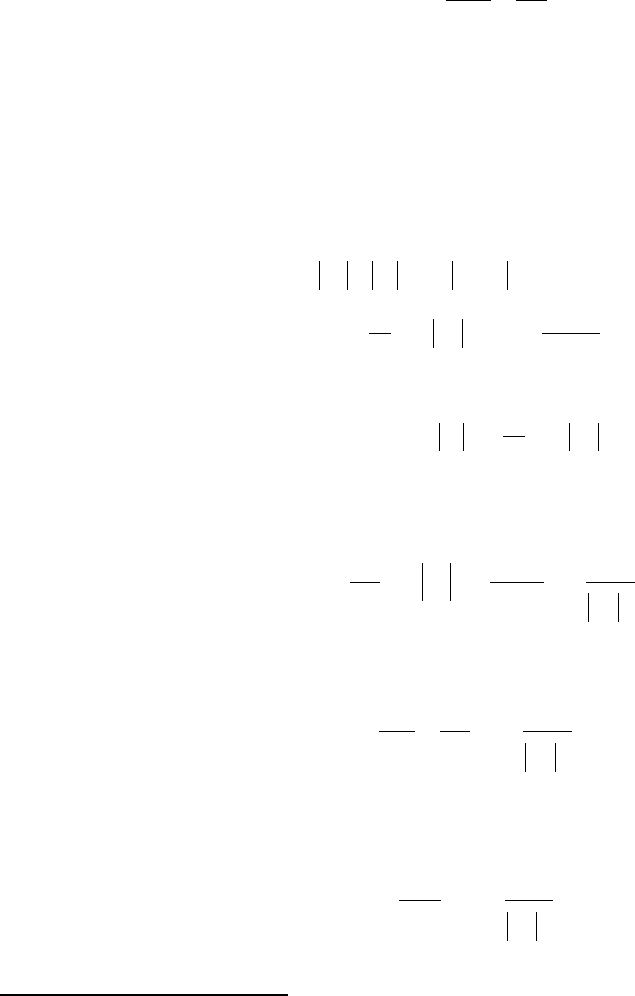
189

браженной входной последовательности

1,1,0, 



Niab

iNi

и амплитуда выходной

последовательности составит

NaA

imf









, поскольку входная последовательность

бинарная. Для входного шума, обладающего временем корреляции в пределах



и дис-

персией



, дисперсия на выходе согласованного фильтра составит величину

222













Nab

imf

. Таким образом, на выходе согласованного фильтра

отношение сигнал-шум по мощности

составит









. (6.40)

Аналогичным образом, амплитуда выходной последовательности ФПБЛ составляет



, а дисперсия шума









222

isl

Согласно теореме Парсеваля и свойству временного сдвига ДПФ периодическая АКФ

произвольной последовательности

110

N

uuu 

периода

связана с энергетическим

спектром последовательности

N

uuu 

с помощью обратного ДПФ:

1,,1,0,

exp

)(































uumR

miip



. (6.41)

В частности













)0(

Использование последнего соотношения вместе (6.38) в выражении для дисперсии шума

на выходе фильтра дает



















ksl

и отношение сигнал-шум на выходе ФПБЛ принимает вид

222



























Теперь можно оценить энергетические потери в ФПБЛ по сравнению с согласованным

фильтром как









. (6.42)

Циклический сдвиг коэффициентов по сравнению со случаем апериодического сигнала

)(

1 iNi





служит для более компактного представления (6.38) путем исключения линейной фазовой экспоненты. В

случае периодического сигнала данный сдвиг означает циклический сдвиг выходного периодического сиг-

нала и, следовательно, не сказывается на ее форме или отношении сигнал-шум.

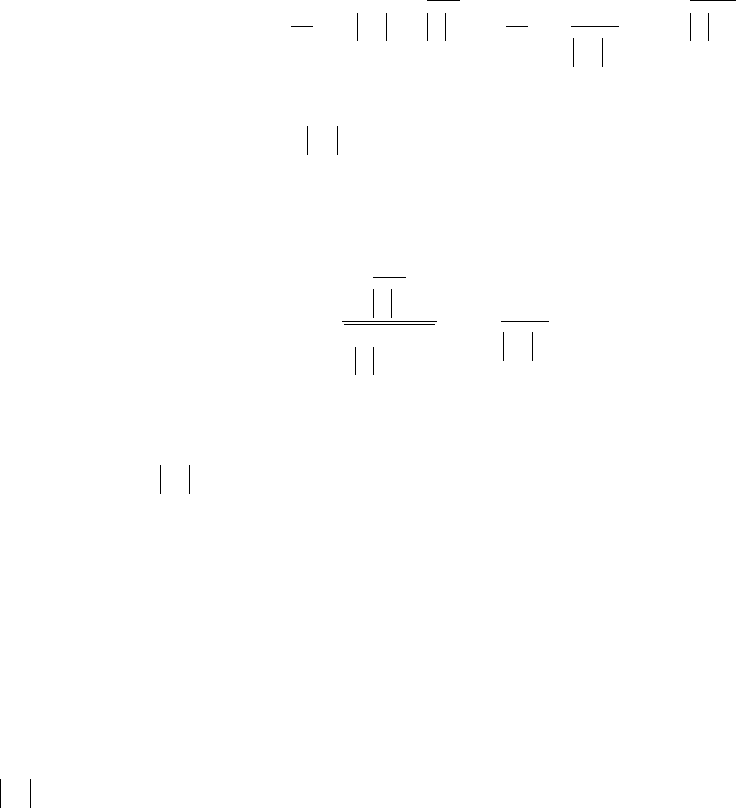
190

Для лучшего понимания последнего результата отметим, что











































отвечают соответственно среднему арифметическому и гармоническому энергетического

спектра последовательности

1,,1,0,

 Nka



. Среднее гармоническое любых неот-

рицательных чисел никогда не превосходит их среднего арифметического, и эти характе-

ристики совпадают, если только все усредняемые числа одинаковы. Следовательно, отно-

шение данных характеристик может служить некоторой мерой степени разброса усред-

няемых чисел. Однако в рассматриваемом случае это отношение























в точности соответствует энергетическим потерям в ФПБЛ. Следовательно, потери в от-

ношении сигнал-шум



определяются неравномерностью энергетического спектра после-

довательности

1,,1,0,

 Nka



, оцениваемой в терминах различия между средним

гармоническим и арифметическим.

Возможность подавления всех периодических боковых лепестков выдвигает новый

критерий синтеза бинарных последовательностей, который является альтернативным ми-

нимизации максимального бокового лепестка

max,p



. Действительно, какой смысл забо-

титься об уровне бокового лепестка, когда все боковые лепестки могут быть приведены к

нулю? Более естественным представляется минимизация затрат, обуславливающих устра-

нение боковых лепестков, и количественной мерой этих затрат, конечно, выступает поте-

ри в отношении сигнал-шум



. Рассмотрим вначале бинарную последовательность (гипо-

тетическую, если

4N

), обладающую равномерным энергетическим спектром:

1,,1,0,

 NkNa



. В свете соотношения (6.41) это означает, что последователь-

ность обладает идеальной периодической АКФ. Абсолютно предсказуемо, что, поскольку

отсутствует объект подавления, то в этом случае ФПБЛ совпадет с согласованным фильт-

ром, не имеющим потерь в отношении сигнал-шум. Соотношение (6.42) подтверждает

данный факт, определяя

1

, или, выраженное в дБ,

0lg10 

дБ

дБ. Поскольку не

существует бинарных последовательностей с идеальной периодической АКФ, то подавле-

ние их боковых лепестков производится за счет потерь в отношении сигнал-шум

)0( 

дБ

, оправдывая введение критерия синтеза

min

Как и во многих задачах, касающихся бинарных последовательностей (см. пара-

граф 6.4), глобально оптимальная бинарная последовательность фиксированной длины

с минимальными потерями



может быть найдена только в результате исчерпывающего

поиска. Данная работа была выполнена для длин вплоть

40N

[48]. Конечно, вследствие

экспоненциального роста вычислительных затрат указанный поиск не может продолжать-

ся далеко за указанный диапазон. Однако известны многие регулярные правила построе-

ния бинарных последовательностей сколь угодно большой длины с очень малыми поте-

рями



(хотя и без гарантии их глобальной оптимальности).

Рассмотрим специальный класс бинарных последовательностей, обладающих

двухуровневой периодической АКФ, т.е. с постоянным уровнем

боковых лепестков











.mod0,

,mod0,

)(

NmR

NmN

(6.43)

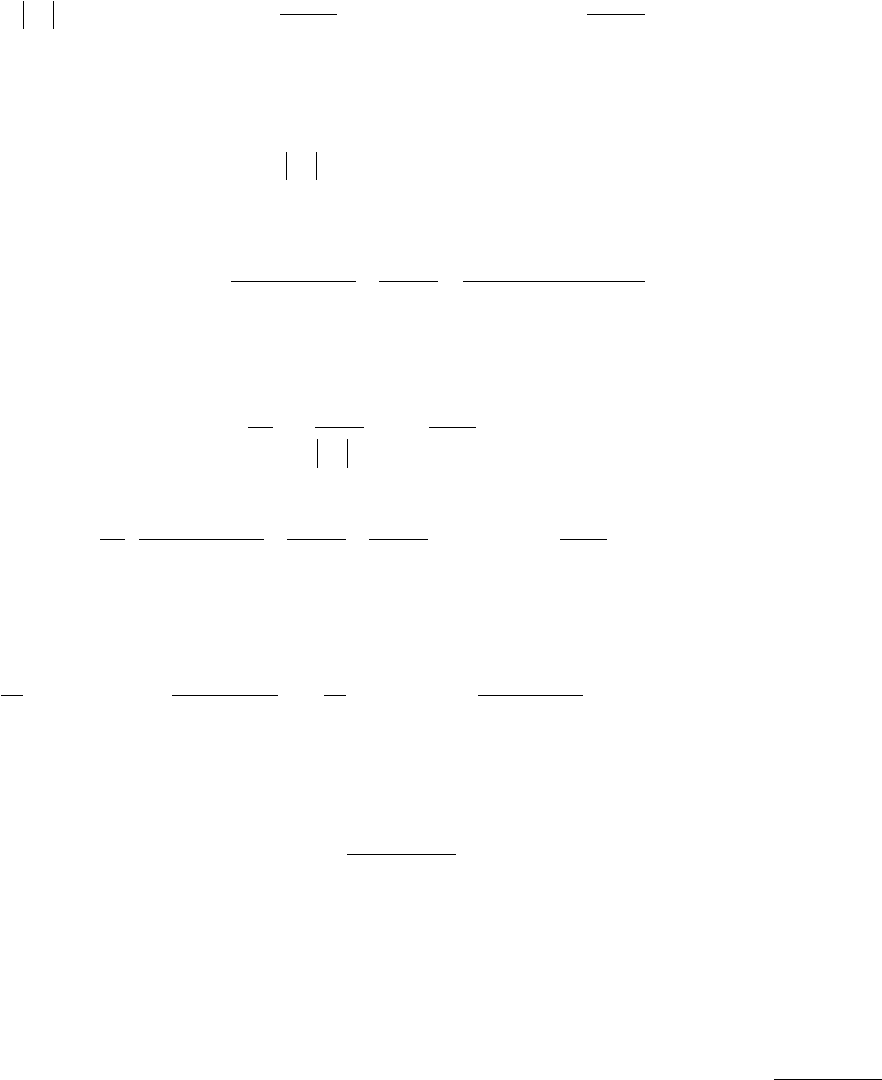
191

Все минимаксные последовательности, как и ряд других, относятся к данному типу. Энер-

гетический спектр такой последовательности, как показывает (6.41), есть просто ДПФ

АКФ:

1,,1,0,

exp

exp)(













































jRRN

jmRa



Последняя сумма уже рассматривалась в 6.11.2 и, как было доказано, она равняется

если

0k

, и нулю в противном случае. Таким образом













.0,

,0,)1(

kRN

kRNN

(6.44)

Подстановка последнего соотношения в (6.42) дает

])1(1)[1(

)2(11

)1(















RNN

, (6.45)

где

NR/

– нормированный уровень бокового лепестка АКФ.

Для определения структуры ФПБЛ, перепишем (6.39) как

1,,1,0,

exp



























и подставим (6.44) в последнее соотношение, тогда

1,,1,0,

exp

)1(

000













































RNRN

RNN



Сумма по

в данном соотношении определяет коэффициенты согласованного фильтра,

поскольку она может быть записана как

1,1,0,

)(2

exp

1)(2

exp























































Nia

kiN



где использован тот факт, что элементы бинарной последовательности вещественны. По-

скольку

произвольный множитель, положим его равным

RN 

. Тогда

1,,1,0,

)1(1











iNi



. (6.46)

Первое слагаемое в данном выражении соответствует последовательности

}{

, считы-

ваемой справа налево, т.е. коэффициентам согласованного фильтра. Таким образом, для

последовательности, обладающей двухуровневой АКФ (6.43), ФПБЛ получается путем

незначительного изменения согласованного фильтра: вычитанием некоторой постоянной

величины из всех коэффициентов. Более того, для бинарных последовательностей данного

типа коэффициенты ФПБЛ принимают только два возможных значения







)1(1

где

– постоянная составляющая последовательности, т.е. разность между числом плюс

и минус единиц на периоде:



 NNa

Как известно из предыдущего материала, существует множество бинарных после-

довательностей с АКФ вида (6.43), для которых

1R

(

– последовательности, после-

довательности Лежандра и другие минимаксные последовательности с АКФ вида (6.12)).

Оценка их потерь в ФПБЛ согласно (6.45) дает

)1/(2  NN

, т.е.

2

(3 дБ) для прак-

тически интересных длин. Отсюда видно, что наиболее популярные минимаксные бинар-

192

ные последовательности не играют значительной роли в свете критерия потерь в ФПБЛ:

половина их энергии теряется при обработке с помощью ФПБЛ.

С другой стороны, при положительном

, достаточно малым в сравнении с

)1/(1 

, т.е. потери оказываются достаточно малыми. Так называемые коды Зингера

служат хорошим примером подобных бинарных последовательностей. Код Зингера суще-

ствует при любой длине вида





и обладает двухуровневой АКФ типа (6.43) со

значением





qNR

, где

pq 

– натуральная степень простого

– натуральное

число. Наиболее интересная с рассматриваемых позиций модификация кодов Зингера от-

вечает

3q

, для которой







125.1









n

, т.е

51.0

дБ

дБ. Как вид-

но, данные коды достаточно привлекательны при обработке их ФПБЛ, поскольку потери в

отношении сигнал-шум, сопровождающие полное подавление боковых лепестков, малы.

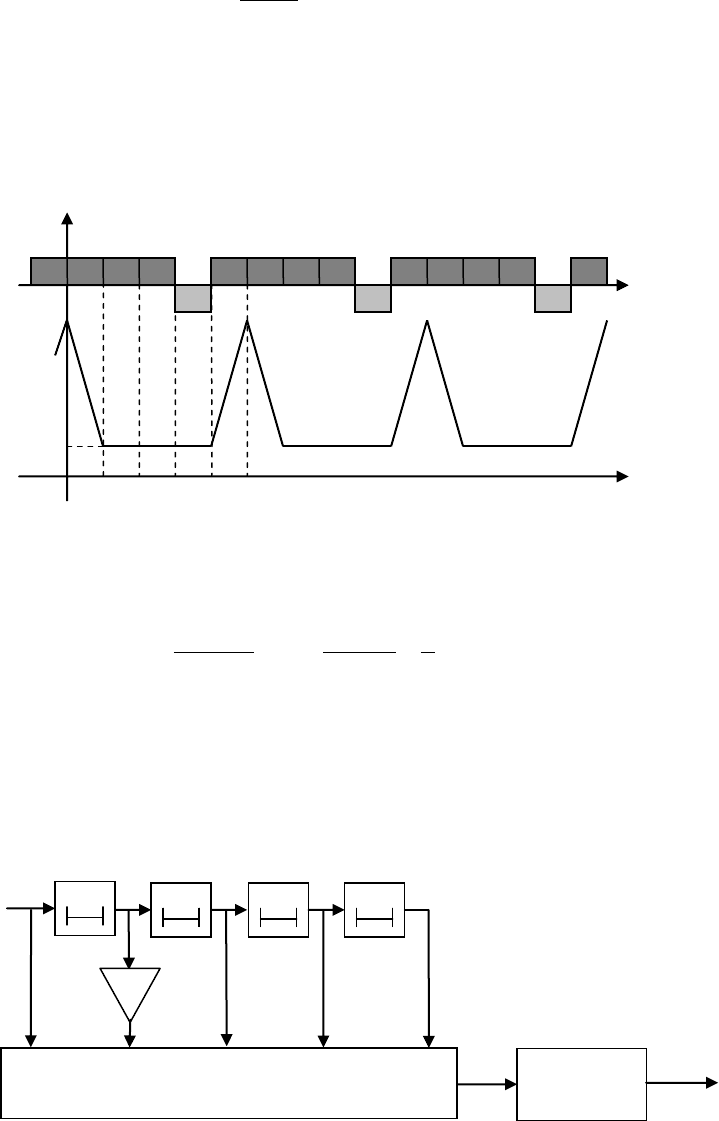
Пример 6.12.1. Рассмотрим периодическую версию бинарного кода Баркера длины

5N

из таблицы 6.1:

1,1,1,1,1 

, для которого

1,4 



, а постоянная состав-

ляющая

a

. Его периодическая АКФ, что может быть проверено непосредственной

проверкой, удовлетворяет соотношению (6.43) со значением

)5/1(1 R

. В действи-

Рис. 6.21. Бинарный сигнал длины

5N

и его периодическая АКФ.







–

)(ts

)(tr

СФОИ

Рис. 6.22 ФПБЛ для последовательности длины N=5.

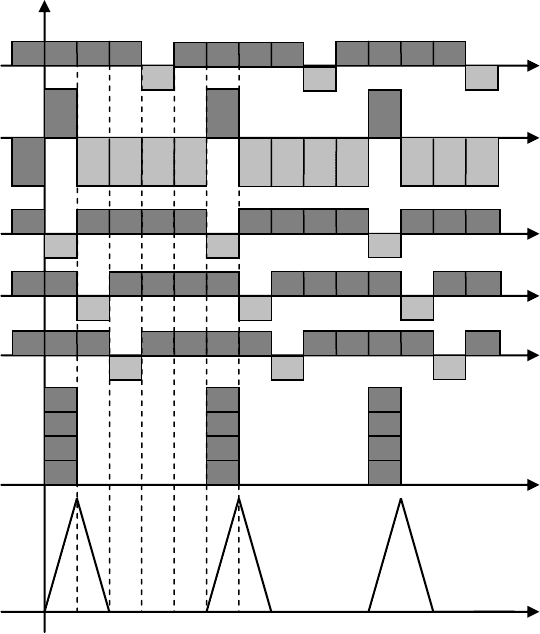
193

тельности данная последовательность представляет собой код Зингера с параметрами

2,4  nq

. Рис. 6.21, b демонстрирует вид АКФ (т.е. отклик согласованного фильтра) пе-

риодического сигнала, модулированного данной последовательностью (рис. 6.21, a). Как

следует из (6.46), согласованный фильтр для данной последовательности легко трансфор-

мируется в ФПБЛ изменением всех коэффициентов +1 на

3/2

и –1 на

3/4

, которое

после соответствующего масштабирования означает замену –1 на –2 при оставлении без

изменения +1 (см. рис. 6.22). Отклик ФПБЛ на тот же сигнал построен на рис. 6.23, на ко-

тором оцифровка диаграмм соответствует точкам на рис. 6.22. Выходной сигнал фильтра

имеет желаемую форму, т.е. нулевой уровень боковых лепестков. Используя соотношение

(6.45), легко определить энергетические потери в ФПБЛ как

1111.19/10 

(0.46 дБ).

Основываясь, как и для кодов Зингера, на отображении линейных рекуррентных

последовательностей над конечными полями на бинарный

}1{

алфавит, было найдено

множество даже более эффективных бинарных кодов. Все они характеризуются одинако-

во привлекательными чертами: простотой структуры ФПБЛ, коэффициенты которого

принимают не более трех различных значений. Не углубляясь далее в детали, которые

достаточно сложны, и отсылая заинтересованного читателя к [49-50], отметим только, что

среди упомянутых последовательностей имеются семейства, обладающие асимптотически

малыми потерями в ФПБЛ:

дБ



дБ при

N

6.13. ЧМ сигналы с оптимальной апериодической АКФ.

Краткое обсуждение сути построения ЧМ сигналов с хорошими корреляционными

свойствами начнем с соотношения (5.20), напоминающего о том, что требование малого

Рис. 6.23 Отклик ФПБЛ для бинарной последовательности N=5.

194

уровня

)(mR

эквивалентно минимизации числа совпадающих частот в кодовой последо-

вательности частот

110

,,,

N

FFF 

и ее копии, сдвинутой на

позиций. Очевидно, что

если число чипов (элементарных импульсов)

(т.е. длина) не превосходит числа различ-

ных частот

, получение нулевого уровня боковых лепестков

0),(  mm

может быть

достигнуто тривиальным путем: использованием частотного кода, все элементы которого

различны. На практике, однако, типичной является ситуация, когда

MN 

, что влечет

за собой повторения элементов

1,,1,0,  NiF



и, следовательно, по меньшей мере,

одно совпадение в сдвинутых копиях частотного кода, т.е.

max,



Поскольку частотная последовательность может быть описана с помощью массива

(решетки) размера

NM 

(см. параграф 5.5), то минимизация

max,a



означает построение

решетки с минимально возможным числом совпадений помеченных элементов в исходной

решетке и ее копии, сдвинутой по горизонтали на

позиций. Одной из ключевых про-

блем является конструирование т.н. радарных решеток (radar arrays), определяемых как

NM 

массивы, имеющие только один помеченный элемент в каждом столбце и

max,



, т.е. с числом упомянутых совпадений не более одного. Данное стремление

понимается как отыскание максимально длинной радарной решетки с фиксированным

значением

, поскольку это означает минимизацию

max,a



при ограничениях на час-

тотный ресурс. Следуя [51], попытаемся доказать простейшую верхнюю границу длины

радарной решетки.

Рассмотрим последовательность

110

,,,

N

FFF 

и отметим, что для получения не

более одного совпадения все разности между номерами позиций, отвечающих одинако-

вым частотам, должны быть различными. Действительно, пусть

tski

FFFF  ,

0 tski

. Тогда в исходной последовательности и ее копии, сдвинутой на

tskim 

позиций, произойдет не менее двух совпадений. Обозначим через

чис-

ло символов (частот) среди

110

,,,

N

FFF 

, повторяющихся

раз. Тогда

MnNin





. (6.47)

Подсчитаем теперь число возможных разностей между номерами позиций, содержащих

идентичные частоты. Если некоторая частота повторяется

раз, то число подобных раз-

ностей для этой частоты будет

)1( ii

. Поскольку в последовательности содержится

частот, повторяющихся

раз, то общее число указанных разностей составит величину





nii )1(

, и так как ни одна из разностей не должна повторяться, то

1)1( 



Nnii

, (6.48)

где правая часть неравенства дает максимальное число не равных положительных разно-

стей среди номеров

}1,,1,0{ N

. Соотношение

3323)1(

 iiiii

не имеет веще-

ственных корней и, следовательно, положительно при любом

. Поэтому сумма

023)1(]23)1([ 



innniiniii

что, с учетом (6.47), (6.48), может быть преобразовано к виду

0231  NMN

, или

13  MN

. (6.49)

В действительности эта граница не является строгой. Известны более точные границы,

например в [52], асимптотический вариант которых приводит к результату

195

620





 MMN

, (6.50)

что снижает правую часть (6.49) приблизительно на

M194.0

Для значений

16M

известны абсолютно точные, т.е. действительно достижимые,

верхние границы длины

. Для указанного диапазона

максимальная длина

max

ра-

дарных решеток ограничена сверху соотношениями [52]















.1614,53

,1310,43

,95,33

,42,23

max

(6.51)

Пример 6.13.1. Частотный код {1, 2, 3, 4, 5, 6, 7, 8, 7, 4, 3, 9, 9, 5, 8, 2, 6, 5, 1, 4, 2, 1,

3, 7}, который определяет номера частот из некоторого алфавита с

9M

или, что экви-

валентно, номера строк в каждой колонке решетки, имеет максимально возможную длину

24N

. Свойства радарной решетки, т.е. наличие единственного совпадения частот при

всех ненулевых сдвигах, может быть проверено путем непосредственной проверки (задача

6.53). 

Кроме того, известны регулярные правила построения радарных решеток длины

MN 5.2

для любого четного

(см. [51]) и для

2/M

, равного произведению простых

чисел, дающего остаток один от деления на 4, т.е.

,58,34,26,10M

Сонарные (sonar) решетки представляют собой обобщение радарных, сохраняющие

свойство «не более одного совпадения» для произвольной комбинации горизонтального и

вертикального сдвига [53]. Практически это требование отражает стремление иметь сла-

бую корреляцию сигнальных копий, сдвинутых как во времени, так и по частоте. Рассмат-

ривая подход к выбору частотного пространства для ЧМ сигналов (параграф 5.5), отмеча-

лось, что частотные сдвиги, вызывающие переход из текущего значения частоты к сосед-

нему, более типичны для сонарных, чем локационных систем. Известно, например, мно-

жество регулярных алгоритмов построения массивов Костаса [54], т.е. квадратных

)( NM 

сонарных массивов или ЧМ последовательностей, имеющих одинаковую длину

и число различных частот.

196

Задачи.

6.1. Частота заполнения прямоугольного импульса длительности

10T

мксек ли-

нейно спадает со 110 до 90 МГц. Вычислить выигрыш от обработки сигнала. Какова при-

близительно длительность сигнала на выходе согласованного фильтра? Изобразить функ-

цию и диаграмму неопределенности.

6.2. Частота заполнения прямоугольного импульса длительности

10T

мксек ли-

нейно спадает со 110 до 90 МГц на первой его половине, а затем линейно возрастает от 90

до 110 МГц на второй. Вычислить выигрыш от обработки сигнала. Изобразить функцию

неопределенности и ее горизонтальные сечения в верхнем и нижнем уровнях.

6.3. Вычислить апериодическую и периодическую АКФ для бинарного кода Барке-

ра длины

11N

наиболее экономным образом.

6.4. Возьмем периодическую последовательность

}{

периода

и сформируем

новую последовательность

}{

, выбирая каждый

–й элемент

}{

dii

ab 

, где произ-

ведение в индексе берется по модулю

. Данная трансформация называется децимирова-

нием

}{

с индексом

. Доказать, что если

}{

обладает идеальной периодической

АКФ, а

взаимно просто с

, то

}{

также будет обладать идеальной периодической

АКФ.

6.5. Бинарный

}1{

код длины

5N

обладает периодической АКФ вида

5mod0,1)(  mmR

. Его апериодическая АКФ принимает значения

0)1( 

1)2( 

. Определить

)3(

)4(

6.6. Бинарный

}1{

код длины

5N

обладает постоянной составляющей

a

1)4( 

. Определить значения

)(mR

и остальные значения

)(mR

6.7. Может ли бинарный

}1{

код нечетной длины

5N

иметь

1)5( 

? Может

ли бинарный

}1{

код четной длины

6N

иметь

1)6( 

? Сформулировать и доказать

для произвольного бинарного кода связь между соотношением трех величин: длины

сдвига

и уровня

)(mR

6.8. Возможно ли, чтобы бинарная

}1{

последовательность имела

1)( mR

3)1( mR

для некоторого сдвига

? Что можно сказать о соотношении между

)(mR

)1( mR

6.9. Возможно ли, чтобы бинарная

}1{

последовательность имела

2)2( 

1)2( 

6.10. Предположим, кто-то определил, что каждая из ФМ последовательностей

длины

100N

в его распоряжении имеет не нормированную периодическую АКФ, при-

нимающую значения

12

при некоторых сдвигах

}1,,2,1{  Nm 

. Может ли среди них

существовать код с

05.0

max,



197

6.11. Построить согласованный фильтр для бинарного ФМ сигнала, манипулиро-

ванного последовательностью вида

}{ 

, и привести диаграммы в характерных точках

для апериодической и периодической версии сигнала на входе фильтра.

6.12. Построить согласованный фильтр для бинарного ФМ сигнала, манипулиро-

ванного последовательностью вида

}{ 

, и привести диаграммы в характерных

точках для апериодической и периодической версии сигнала на входе фильтра.

6.13. Студент вычислил периодическую АКФ бинарной

}1{

последовательности

длины

21N

и получил следующие значения

9)(

mR

3)(

mR

5)(

mR

7)(

mR

7)(

mR

. Могут ли все эти результаты оказаться правильными? Какие из

них несомненно не правильные?

6.14. Доказать не существование минимаксных бинарных последовательностей

1)( mR

1,,2,1  Nm 

длин

45,37,33,29,21,17N

. (При доказательстве использо-

вать тот же метод, что и при определении необходимых условий идеальности АКФ би-

нарных последовательностей).

6.15. Доказать, что децимирование минимаксной бинарной последовательности

вновь дает минимаксную бинарную последовательность, если индекс децимации взаимно

прост с периодом

6.16. Доказать, что операция децимации любой периодической последовательности

не изменяет величины максимального бокового лепестка, если индекс децимации взаимно

прост с периодом

6.17. Вычислить

1)476(5)73( 

в поле

)11(GF

6.18. Решить уравнение

1)245(76





в поле

)11(GF

6.19. Доказать, что поле

)4(GF

не может быть построено на основании операций

по модулю 4.

6.20. Является ли последовательность длины

7L

вида

}0100110{

двоичной

–

последовательностью? Каков будет ответ в случае замены всех нулевых элементов на

единичные и наоборот?

6.21. Построить двоичную

– последовательность длины

15L

с начальным со-

стоянием

0,1

3210

 dddd

, нарисовать структуру ее генератора и составить таблицу,

описывающую изменение состояний генератора.

6.22. Доказать, что на одном периоде бинарной m–последовательности памяти n

число серий последовательных символов (01), (10), (11) встречается

n

раза, а число

серий (00) – на единицу меньше.

6.23. Наблюдается

– последовательность, о которой известны алфавит и значе-

ние памяти, но неизвестны коэффициенты рекурсии (6.13). Каково минимально необхо-

димое и достаточное число наблюдаемых символов для определения значений этих коэф-

фициентов?