Ипатов В.П. Широкополосные сигналы
Подождите немного. Документ загружается.


167
вательность
}{
i
d
памяти
n
, т.е. длины
12
n
L
. Отобразим ее символа 0 и 1 в бинарный
алфавит
1
согласно правилу
,1,1
,0,1
)1(
i
i
d
i
d
d
a
i
(6.15)
где при возведении (–1) в степень
i
d
последнее трактуется как вещественное число 0 или
1. Полученная в результате подобного преобразования последовательность
}{
i
a
вещест-
венных бинарных символов
1
обладает периодом
12
n
LN
и является однознач-
ным отображением исходной двоичной
m
– последовательности
}{
i
d
. Было бы вполне ес-
тественным сохранить за ней то же самое название бинарной
m
– последовательности.
Для исключения перепутывания можно было бы использовать дополнительное обозначе-
ние вида бинарная
}1{
и бинарная
}1,0{
последовательности. Определим теперь ненор-
мированную периодическую АКФ (6.7) последовательности
}{
i
a
:
1
0
1
0
1
0
)1()1()1()(
L
i
dd
L
i
dd
N
i
miip
miimii
aamR
. (6.16)
Теперь можно привлечь свойство сдвига и сложения бинарных
}1,0{
m
– последователь-
ностей. Сложение показателей степеней здесь осуществляется по модулю 2, поскольку
получается тот же результат от возведения в степень, что и при обыкновенном арифмети-
ческом сложении. Однако
}{}{
miii
ddd
представляет собой бинарную
}1,0{
m
– по-
следовательность периода
L
при
Lm mod0
, или последовательность из одних нулей в
противном случае. Вследствие свойства сбалансированности на одном периоде
}{}{
miii
ddd
содержится
12
1
0
n
L
нулей и
1
1
2
n
L
единиц, поэтому сумма
(6.16) состоит из
0
L
«+1» и
1
L
«–1» при
Nm mod0
, так что
.mod0,1
,mod0,
)(
10
Nm
NmN
LLmR
p
Как можно видеть, данное выражение в точности совпадает с (6.12), подтверждая
тем самым, что бинарные
m
– последовательности являются минимаксными.
1
Пример 6.7.1. Рассмотрим снова последовательность из примера 6.6.1. Ее отобра-
жение на алфавит
}1{
в соответствие с (6.15) дает бинарную
}1{
m
– последователь-
ность
,1,1,1,1,1,1,1
. Табл. 6.3, содержащая только минимально необходимое
1
Обобщение отображения (6.15) на случай последовательностей над
2),( ppGF
представимо как
)/2exp( pdja
ii
, приводя к многофазным (p–фазным) кодам, периодическая АКФ которых также
удовлетворяет (6.12). Однако многофазные коды этого типа с
2p
менее интересны с практической точки
зрения, чем минимаксные бинарные последовательности.
Таблица 6.3. Вычисление периодической АКФ бинарной m-последовательности.
m
0
a
1
a
2
a
3
a
4
a
5
a
6
a
)(mR
p
0
–
+
+
–
+
–
–
+7
1
–
–
+
+
–
+
–
–1
2
–
–
–
+
+
–
+
–1
3
+
–
–
–
+
+
–
–1

168
число записей, иллюстрирует вычисление периодической АКФ последовательности.
Представляет также интерес рассмотрение процесса согласованной фильтрации дискрет-
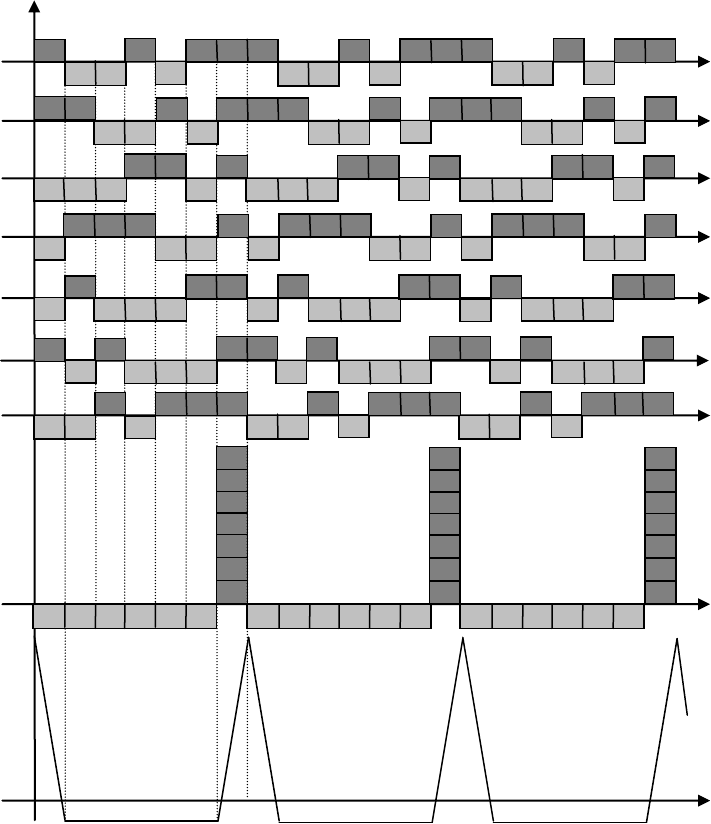
ного сигнала, модулированного данной бинарной последовательностью. На рис. 6.14 изо-
бражен подобный фильтр, согласованный с одним периодом периодического видеосигна-
ла с прямоугольными чипами. Все блоки данной структуры абсолютно идентичны схеме,
представленной на рис. 6.7. Диаграммы напряжений в характерных точках фильтра пока-
заны на рис. 6.15. Как видно, выходной сигнал обладает основными лепестками, повто-
ряющимися с периодом
N
и равномерным боковым лепестком отрицательной полярно-
сти, уровень которого в семь раз меньше основного.
Бинарные
m
– последовательности относятся к числу наиболее популярных дис-
кретных сигналов, применяемых в современной информационной технологии, благодаря
своим оптимальным периодическим корреляционным свойствам и простоте формирова-
ния и обработки. Возможно, одним из наиболее ярких примеров их практического исполь-
зования является система мобильной связи 2-го поколения cdmaOne (IS-95), в которой в
качестве пилот–сигналов для начальной синхронизации, мультиплексирования сигналов
базовых станций и скремблирования данных применяются
m
– последовательности раз-
личной длины.
В дополнение к этому,
m
– последовательности образуют базис для формирования
других важных семейств сигналов (Касами, Голда и др., см. главу 7).
В то же время, множество длин
,1023,511,255,127,63,31,15,7,312
n
N
, при
которых существуют данные последовательности, достаточно разрежено, что в некоторых
случаях может оказаться ограничительным фактором к практическому использованию. В
связи с этим представляет интерес рассмотреть еще один класс бинарных минимаксных
последовательностей, что, однако, потребует дополнительных сведений о теории конеч-
ных полей.
)(ts
–
–
+
–
+
+
–
1
2
3
4
5
6
7
)(tr
СФОИ
8
9
Рис.6.14. Согласованный фильтр для бинарной m- последовательности.
169
2
3
4
5
6
7
8
9
Рис.6.15. Процедура согласованной фильтрации.
t
1
t
t
t
t
t
t
t
t
170
6.8. Дополнительные сведения о конечных полях.
Возьмем некоторый элемент
x
конечного поля
)(pGF
и умножим его сам на себя
m
раз, присвоив результату наименование
m
–й степени элемента
x
:
m
m
xxxx
раз
.
Стандартные правила обращения со степенями обычной алгебры сохраняют свою спра-
ведливость и в полях, включая и конечные. В частности
nm
nmnm
nm
xxxxxxxxxxxx
разразраз
,
mn
n
mmm
n
m
xxxxx
раз
.
Более того, обозначая
n
–ю степень
)0(
1
xx
как
n
x
, имеем
разnразm
nm
xxxxxxxx
111
.
Тогда неоднократное использование определение обратного элемента
1
1
xx
приводит к
соотношению
nm
mn
nm
nm
x
nmx
nmx
xx
,,)(
,,
1
.
Аналогичным образом из
mmmm
разmразm
xxxxxxxxx
1
111
и единственности обратного элемента любому ненулевому следует, что
mm
xxx
1
0
и1
.
Пример 6.8.1. В поле
)5(GF
(см. таблицы на рис. 6.11)
12
0
,
22
1
,
4222
2
,
324222
23
,
123222
34
;
32
1
,
43)2(2
2212
,
2343)2(2
3313
,
1323)2(2
4414
.
Рассмотрим теперь последовательные степени элемента
0x
поля
)(pGF
:
,,,1
210
xxx
. Поскольку все члены этой серии принадлежат
)(pGF
, то они не могут
быть все различными и, следовательно, для некоторых
ki
будет выполняться равенство
1
kiki
xxx
. Предположим, что существует элемент
, у которого первые
1p
степеней
2210
,,,,1
p
все различны. Поскольку
1p
в точности равно числу
ненулевых элементов
)(pGF
, то вышеприведенные степени в точности исчерпывают все
ненулевые элементы
)(pGF
. Таким образом, элемент
, если он действительно сущест-
вует, позволяет построить все поле
)(pGF
, за исключением нулевого элемента, посредст-
вом возведения
в степени
2,,1,0 p
. Подобный элемент получил название прими-
тивного элемента.
Одним из наиболее важных положений о конечных полях является то, что в любом
из них содержится примитивный элемент. Доказательство данного положения может быть
найдено во многих книгах по современной алгебре или теории кодирования (например,
[30, 32, 33]). Примитивный элемент не является единственным: в любом конечном поле,
порядок которого превышает 3, имеется более одного примитивного элемента. Например,
как видно из примера 6.8.1, как элемент 2, так и 3 являются примитивными в поле
)5(GF
.
171
Поскольку для примитивного элемента степени
2210
,,,,1
p
исчерпыва-
ют все ненулевые элементы
)(pGF
, то
1
p
должен быть равен какому-то из них. В дей-
ствительности он не может быть равен никакому другому, кроме 1, поскольку равенство
lp
1
при
20 pl
означает, что
1
1
lp
. Однако это не возможно, поскольку
111 plp
и среди элементов
221
,,,
p
не может быть равного единице.
Следовательно,
1
1
p
. Теперь легко увидеть, что подобное утверждение верно для лю-
бого ненулевого элемента конечного поля, а не только для примитивного. Действительно,
любой ненулевой элемент
)(pGFx
представим как
l
–я степень примитивного элемента
для соответствующего целого
l
:
l
x
, так что (малая теорема Ферма)
1)()(
1)1(11
lpplplp
x
. (6.17)
Следующее определение имеет совершенно естественное наименование, полно-
стью совпадающее с категорией обычной алгебры. Целое значение показателя
l
, в кото-
рое возводится
для получения
l
x
, называется логарифмом
x
по основанию
с ис-
пользованием обозначения
x
log
. Следовательно,
x
x
log
.
Рассмотрим теперь только простые поля нечетного порядка
)2( p
и введем поня-
тие двузначного характера
)(x
ненулевого элемента
x
, определяемое как
x
x
x
x
log
)1(
,2mod0log,1
,2mod0log,1
)(
. (6.18)
Ясно, что двузначный характер представляет собой просто отображение поля
)(pGF
на
пару вещественных чисел
}1,1{
, превращая ненулевой элемент
x
в +1, если его лога-
рифм четен, и в –1 в противном случае. Очевидно, что подобное отображение зависит от
конкретного выбора примитивного элемента (задача 6.24). В дальнейшем будут использо-
ваны следующие свойства двузначного характера.
1. Значение характера от единичного элемента поля
)(pGF
всегда равно единице:
1)1(
. (6.19)
Справедливость подобного утверждения непосредственно вытекает из следующего соот-
ношения
01log1
0
.
2. Характер является мультипликативной функцией, т.е. характер от произведения
двух ненулевых элементов есть произведение их характеров. Действительно, из (6.17) и
(6.18) следует
)()()1()1()1()1()(
loglogloglog)(log
yxxy
yxyxxy
. (6.20)
3. Свойство сбалансированности: сумма характеров всех ненулевых элементов по-
ля
)(pGF
равна нулю:
0)1()(
1
1
log
1
1
p
x
x
p
x
x
. (6.21)
Доказательство данного равенства основано на том факте, что при переборе
x
всех
1p
ненулевых значений
x
log
пробегает в некотором порядке по диапазону из
1p
целых
чисел вида
2,,1,0 p
. Вследствие нечетности
p
число целых чисел в указанном диапа-
зоне четно, так что
2/)1( p
из них являются четными и
2/)1( p
– нечетными. Следова-
тельно, выше приведенная сумма содержит одинаковое число плюс и минус единиц и,

172
значит, равна нулю.
4. Рассмотрим характер элемента, противоположного единице, т.е.
)1(
. По-
скольку все элементы
2,,1.0, pi
i
различны, то только два из них удовлетворяют
уравнению
1
2
x
, а именно 1 и –1, а само уравнение удовлетворяет значению
2
)1(
p
,
причем последний элемент не может быть иным, чем –1. В результате получаем, что
2
1
)1(log
p
и выражение
.4mod3,1
,4mod1,1
)1()1(
2
1
p
p
p
(6.22)
Пример 6.8.2. Продолжая пример 6.8.1, отметим, что в поле
)5(GF
1)3()2(
, а
1)4()1(
. Тогда в соответствие со свойством мультипликатив-
ности
1)1()1()4()2(1)3()42(
и согласно свойству сбалансирован-
ности
0)4()3()2()1(
. Кроме того,
1)4()1(
, что согласуется с (6.22),
поскольку
1145
.
Другим наименованием двузначного характера, особенно популярного в теории
чисел, является символ Лежандра, что объясняет название последовательностей, рассмат-
риваемых в следующем параграфе.
6.9. Последовательности Лежандра.
Сформируем бинарную последовательность нечетной простой длины
pN
, ото-
ждествляя номер позиции
i
элемента
1
i
a
с элементом простого поля
)(pGF
. Тогда
для любого
}1,,2,1{ Ni
определен характер
)(i
и последовательность Лежандра
есть просто последовательность характеров номеров
i
за исключением
0i
, для которого
элемент последовательности устанавливается равным +1
1
. Для периодической версии по-
следовательности Лежандра правило формирования определяется в виде
.mod0),(
,mod0,1
Nii
Ni
a
i
(6.23)
Периодичность последовательности (6.23) с периодом
N
следует из трактовки номеров
i
в
)(i
как элементов
)(pGF
, причем сложение выполняется по модулю
p
, в результате
чего приходим к выражению
)()()( ipiNi
.
Для исследования периодической АКФ последовательности Лежандра подставим
(6.23) в (6.7) и вынесем из-под знака суммы члены, содержащие
0
a
:
1
1
1
1
00
1
0
)()()()()(
p
i
N
i
miimm
N
i
miip
mimi
miimmaaaaaaaamR
.(6.24)
Очевидно, что интересно оценить только уровень боковых лепестков, т.е. при тех сдвигах
m
, когда они не кратны
pN
. Применение свойства мультипликативности (6.20) дает
)()1()( mm
и
)1()()]1([)(
11
miimiimi
, где всегда определен об-
ратный элемент, поскольку нулевое значение
i
вынесено из–под знака суммы в (6.24). В
1
Другой выбор, приводящий к аналогичному конечному результату, состоит в присваивании этому элемен-
ту значения –1.
173
результате получаем
1
1
12
)1()()]1(1)[()(
p
i
p
mi
miimmR
. (6.25)
Обратимся теперь к (6.22). Для любой длины вида
4mod1 pN
1)1(
и первое сла-
гаемое в вышеприведенном соотношении равно
2)(2 m
для любого
Nm mod0
. С
другой стороны, для длин типа
4mod3N
1)1(
и то же самое слагаемое в (6.25)
аннулируется. Для вычисления второго слагаемого в (6.25) отметим, во–первых, что для
любого ненулевого
i
из
)(pGF
1)(
2
i
. Во–вторых, при пробегании
i
по всем ненуле-
вым элементам
)(pGF
1
i
, как и
)mod0(
1
pmmi
, также пробегают указанный диапа-
зон, но в некотором другом порядке. Следовательно,
1
1
mi
пробегает множество
1p
элементов поля, включая нуль, но исключая 1, поскольку
1
mi
не может принимать ну-
левого значения. В действительности же нулевой элемент также должен быть исключен из
числа возможных значений
1
1
mi
, поскольку
i
во втором слагаемом (6.24) не принима-
ет значения
mi
, отвечающего
01
1
mi
, тогда полный диапазон значений
1
1
mi
простирается от 2 до
1p
. Резюмируя все вышесказанное, приходим к следующему ре-
зультату
1
1
1
1
1
2
12
1)1()()()1()(
p
i
p
x
p
x
mi
xxmii
,
где завершающий шаг следует из свойств характера (6.19) и (6.21). В итоге периодическая
АКФ последовательности Лежандра оказывается возможной одного из двух типов:
1. Если длина имеет вид
)4mod1т.е.(14 NhN
, то
;mod0,1или3
,mod0,
)(
Nm
NmN
mR
p
(6.26)
2. Если же длина представима как
)4mod3т.е.(34 NhN
, то
;mod0,1
,mod0,
)(
Nm
NmN
mR
p
(6.27)
где
h
– натуральное число.
Последний результат, повторяющий (6.12), демонстрирует, что последовательности
Лежандра длин
34 hN
являются минимаксными, т.е. обладают оптимальными перио-
дическими корреляционными свойствами возможными для бинарных последовательно-
стей нечетных длин.
Пример 6.9.1. Длина
7N
принадлежит множеству вида
34 hN
. В поле
)7(GF
элемент 3 является примитивным, поскольку возведение его в степень 0, 1, …, 5
дает все различные ненулевые элементы:
53,43,63,23,33,13
543210
. Как
непосредственно следует из этой серии, логарифмы 1, 2, и 4 четны, тогда как 3, 5 и 6 – не-
четны. Следовательно,
1)4()2()1(
, а
1)6()5()3(
. Теперь, согласно
(6.23), расстановка плюс единицы на позициях
4,2,1,0i
и минус единицы на позициях
6,5,3i
дает последовательность Лежандра длины
7N
. Вычисления, иллюстрируемые
табл. 6.4, подтверждают оптимальность корреляционных свойств полученной бинарной
последовательности.
Последовательности Лежандра образуют достаточно мощный класс бинарных ко-

174
Таблица 6.4. Вычисление периодической АКФ последовательности Лежандра.
m
0
a
1
a
2
a
3
a
4
a
5
a
6
a
)(mR
p
0
+
+
+
–
+
–
–
+7
1
–
+
+
+
–
+
–
–1
2
–
–
+
+
+
–
+
–1
3
+
–
–
+
+
+
–
–1
дов с минимаксной периодической АКФ. Условие их существования (любая простая дли-
на вида
34 hN
) значительно мягче, чем у
m
– последовательностей
)12(
n
N
,
благодаря чему последовательности Лежандра более доступны по сравнению с
m
– по-
следовательностями. Например, на интервале длин от 50 до 1500
m
– последовательности
существуют только при пяти значений длин, тогда как доступное число последователь-
ностей Лежандра составляет 114.
6.10. Бинарные коды с хорошей апериодической АКФ (продолжение).
После накопления необходимых знаний о бинарных последовательностях с хоро-
шими периодическими АКФ можно возвратиться к идее, сформулированной в 6.4 и за-
ключающейся в использовании этих последовательностей в качестве исходного материала
для поиска кодов с привлекательной апериодической АКФ. Рассмотрим некоторую после-
довательность
110
,,,
N
aaa
длины
N
. Любой ее циклический сдвиг
11,,,,,,,
1011
Nsaaaaa
sNss
, обладает такой же периодической АКФ, что и
исходный код, поскольку периодическая АКФ инвариантна к циклическому сдвигу (см.
задачу 5.5). Апериодическая же АКФ циклически сдвинутой копии может отличаться от
АКФ первоначальной. Вместе с границей (6.5) данный факт устанавливает основу для
распространенного алгоритма поиска кодов с приемлемой апериодической АКФ, описан-
ного ниже.
На первом шаге для заданной длины
N
некоторым образом формируется множе-
ство последовательностей кандидатов с хорошей периодической АКФ. Оно может вклю-
чать все известные последовательности заданной длины
N
[35-37], уровень боковых ле-
пестков периодической АКФ которых, согласно (6.5), позволяет надеяться на получение
низкого значения
max,a
или быть ограниченным в соответствии технологическими
предпочтениями проектировщика. Например, если необходимы бинарные коды длины
63N
, то первоначальное множество может быть ограничено только всеми
m
– после-
довательностями данной длины (при указанной длине не существует последовательность
Лежандра, т. к.
N
не простое число) или включать некоторые другие последовательности
с удовлетворительной периодической АКФ. Если же необходима длина
127N
, то мно-
жество может охватывать все
m
– последовательности наряду с последовательностями
Лежандра
1
или содержать другие последовательности с достаточно низкими периодиче-
скими боковыми лепестками.
1
При одной и той же степени могут существовать различные примитивные полиномы, каждый из которых
генерирует отличные
m
–последовательности одной и той же длины. Следовательно, при фиксированной
длине могут существовать несколько
m
–последовательностей, и все они подходят для поиска хороших
апериодических кодов. В отличие от предыдущего существуют только две последовательности Лежандра
одинаковой длины, отличающиеся значением первого символа (+1 в одной из них и –1 в другой (см. сноску
на стр.172)).
175
На втором этапе осуществляется исчерпывающий поиск по критерию наименьшего
уровня максимума бокового лепестка апериодической АКФ среди всех однопериодных
сегментов последовательностей кандидатов. В частности, берется однопериодный сегмент
первой последовательности кандидата, вычисляется его апериодическая АКФ и запомина-
ется в памяти уровень максимального бокового лепестка наряду с номерами последова-
тельности кандидата и его сдвига. Затем осуществляется циклический сдвиг сегмента на
одну позицию, и производятся все необходимые вычисления. Если новое значение макси-
мума апериодического бокового лепестка окажется ниже предыдущего, то его значение и
номер нового сдвига заменяют ранее записанные в памяти данные, в противном случае
зарегистрированные значения сохраняются без изменения. Данная процедура повторяется
N
раз, т.е. для всех циклических сдвигов первой последовательности кандидата, после
чего подобному исследованию подвергается следующая последовательность кандидат и
т.д. Результатом поиска служит последовательность с минимальным значением
max,a
среди всех последовательностей, отобранных на первом этапе. Очевидно, отсутствуют га-
рантии того, что полученный результат будет наилучшим среди всех возможных бинар-
ных последовательностей данной длины.
Данная процедура, впервые предложенная в начале 60-х годов, в последствие ши-
роко использовалась многими авторами, постепенно охватывая все более и более обшир-
ное множество кандидатов среди бинарных последовательностей. Один из наиболее под-
робных списков бинарных кодов, синтезированных подобным образом, может быть най-
ден в [34].
Пример 6.10.1. Длина
712
3
N
удовлетворяет условию существования
m
–
последовательности. Имеются два примитивных бинарных полинома степени 3:
1)(
3
xxxf
и
1)(
23
xxxf
. Непосредственная проверка показывает, что
m
– по-
следовательности, порождаемые ими, являются зеркальным отображением друг друга, т.е.
одна из них получается из другой считыванием справа налево. Подобное преобразование
не изменяет ни периодическую, ни апериодическую АКФ (см задачу 5.5). Следовательно,
достаточно включить во множество кандидатов только одну
m
– последовательность, на-
пример, построенную в примере 6.7.1:
1,1,1,1,1,1,1
. Кроме того,
7N
является
простым числом, удовлетворяющим соотношению
34 hN
, при котором также сущест-
вуют и минимаксные последовательности Лежандра, т.е. последовательность, полученная
в примере 6.9.1:
1,1,1,1,1,1,1
, а также ее копия с первым символом, замененным
–1. Последняя полностью повторяет выбранную
m
– последовательность, тогда как пер-
вая – после замены знаков всех элементов – совпадает с циклически сдвинутым зеркаль-
ным отображением
m
– последовательности. Поскольку изменение полярности также не
затрагивает ни периодическую, ни апериодическую АКФ (см. задачу 5.5), то из четырех
возможных кандидатов в множество для анализа достаточно включить только одну мини-
максную последовательность. Пусть это будет последовательность Лежандра, начинаю-
щаяся символом +1. Вычисление ее апериодической АКФ дает следующие значения
1,1,2,1,0,1,0:6,,2,1),( mmR
a
и
7/2
max,
a
. После циклического сдвига
влево последовательность превращается в
1,1,1,1,1,1,1
, а вычисления приводят
к следующему результату
3)4(
a
R
,
7/3
max,
a
, т.е. максимальный апериодический
боковой лепесток хуже, чем у исходного кода. Следующий циклический сдвиг дает
1,1,1,1,1,1,1
и
2)1(
a
R
,
7/2
max,
a
, т.е. аналогично первоначальному ре-
зультату. После следующего сдвига приходим к последовательности
1,1,1,1,1,1,1
, имеющей апериодическую АКФ с боковыми лепестками
0;1,0)( mmR
a
, т.е. с
7/1
max,
a
. Данная последовательность является глобально
оптимальной среди всех ФМ кодов, поскольку ни один из подобных кодов не может иметь
176
меньший уровень максимального апериодического бокового лепестка (см. (6.4)). Действи-
тельно, найден код Баркера длины 7, который является зеркальной копией последователь-
ности, приведенной в табл. 6.1.
Пример 6.10.2. Предположим, что
1464257 N
. Поскольку число 257 про-
стое, то существуют две последовательности Лежандра данной длины, отличающиеся
только первым символом. Вместе с тем,
N
представимо в виде
14 h
и, следовательно,
максимальный боковой лепесток ПАКФ этих последовательностей составляет величину
257/3/3
max,
N
p
(см. (6.26)). Несмотря на это упомянутые последовательности мо-
гут рассматриваться как перспективные с точки зрения
max,a
, поскольку нижняя граница
(6.4) устанавливает
257/5.1
max,
a
. Применение ранее описанной процедуры приводит
к последовательности с максимальным ненормированным апериодическим боковым лепе-
стком, равным 12, т.е.
257/12
max,
a
или –26.6 дБ (сравним полученный результат с
наиболее длинным бинарным кодом Баркера, для которого
13/1
max,
a
или –22.3 дБ).
Последовательность, получаемая после отбрасывания последнего символа, превращается
в код длины
256N
с тем же значением максимального не нормированного бокового ле-
пестка и, значит,
64/3256/12
max,
a
, т.е. снова приблизительно –26.6 дБ. Апериоди-
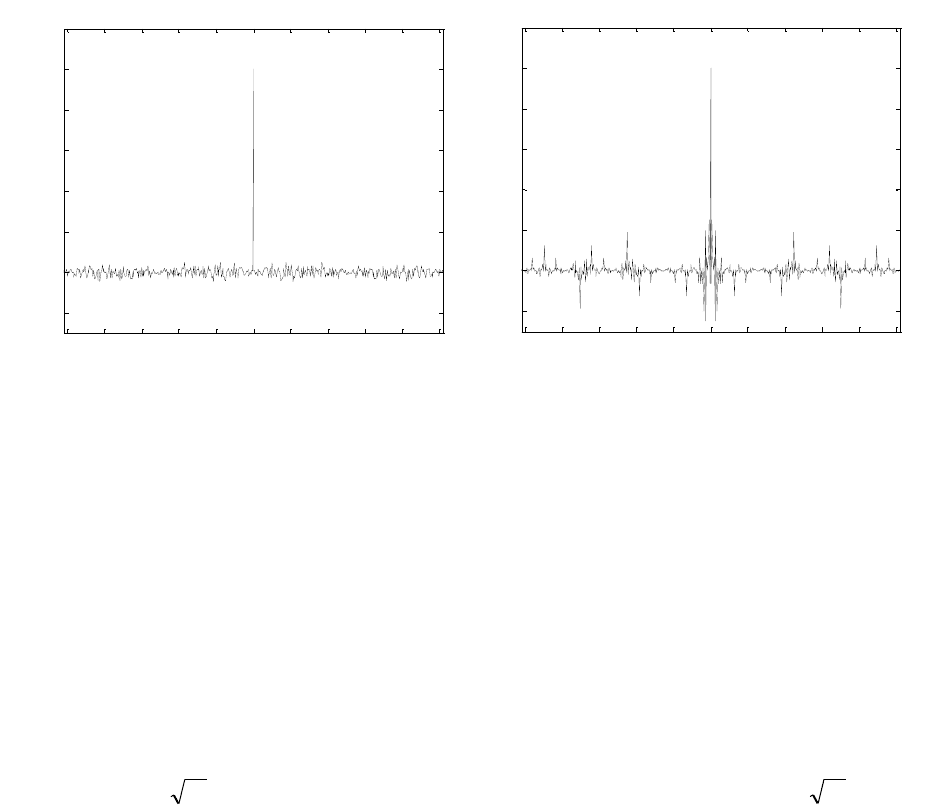
ческая АКФ данного кода показана на рис. 6.16, a. Интересно, что в стандарте UMTS 3-го
поколения в качестве кода первичной синхронизации используется бинарная последова-
тельность точно такой же длины
256N
, обладающей апериодическими боковыми лепе-
стками вплоть до
4/1
(рис. 6.16, b), т.е. значительно большими в сравнении с только что
найденной последовательностью. С другой стороны, выбор кода для поиска соты в UMTS
производился с учетом многих других требований, включая реализационные, которые,
возможно, перевесили критерий хорошей автокорреляции.
На рис. 6.17 представлен еще один иллюстративный материал по оптимизации би-
нарных кодов с точки зрения максимального бокового лепестка апериодической АКФ,
демонстрирующий зависимость
max,a
от длины
N
для предположительно лучших би-
нарных последовательностей, взятых из [25-27, 34]. Пунктирная линия отвечает кривой
N
a
/77.0
max,
, аппроксимирующей зависимость
)(
max,
Nf
a
как
Na/
со значе-
нием
a
, найденным с помощью метода наименьших квадратов. Как следует из рисунка,
-250 -200 -150 -100 -50 0 50 100 150 200 250
-0.2
0
0.2
0.4
0.6
0.8
1
-250 -200 -150 -100 -50 0 50 100 150 200 250
-0.2
0
0.2
0.4
0.6
0.8
1
a)
b)
Рис.6.16. Апериодическая АКФ двух бинарных кодов длины 256: код из примера
6.10.2 (a) и код первичной синхронизации UMTS (b).
