Ипатов В.П. Широкополосные сигналы

Подождите немного. Документ загружается.

147

Задачи.

5.1. Дискретный сигнал длины

5N

имеет комплексные амплитуды вида

jajajajaja  1,1,1,1,1

43210

и частоты

4,3,2,1,0,0  iF

. Опре-

делить значения фаз и амплитуд его элементарных символов (чипов) и классифицировать

сигнал по способу модуляции.

5.2. Дискретный сигнал задан своими амплитудно-фазовым и частотным кодами

вида

 ,1,0,1,,0],2/)1(exp[  iFiija

. Вычислить значения его амплитуд и

фаз. Классифицировать сигнал по способу его модуляции. Является ли данный сигнал пе-

риодическим? Если да, определить величину периода.

5.3. Доказать четность периодической и апериодической автокорреляционных

функций кодовых последовательностей АФМ сигналов.

5.4. АФМ сигнал состоит из прямоугольных чипов длительности



и опреде-

ляется кодовой последовательностью, заданной вектором

)1,0,0,1,0,1,1( a

. Вычислить и

построить его апериодическую и периодическую АКФ. Повторить операции для случая

2/

5.5. Что произойдет с периодической и апериодической АКФ АФМ сигнала при

следующих трансформациях кодовой последовательности:

а) циклическом сдвиге элементов;

б) изменении знака всех элементов;

в) изменении знака только у элементов с четными позициями;

г) умножении всех элементов на одну и ту же константу;

д) зеркальном отображении последовательности (т.е. считывании справа налево)?

5.6. Возможна ли для ФМ кода комбинация

1)1(,3)1( 

? Что можно ска-

зать о комбинациях

6.08.0)1(,1.2)1( jRR



;

jRjR

 1.1)1(,8.06.0)1(

? Ка-

ково возможное значение

)1()1(

RR 

для ФМ кода?

5.7. Расстояния между частотами ЧМ сигнала кратны величине

 /1F

. Доказать,

что последовательность согласованных по времени прямоугольных импульсов с различ-

ными частотами ортогональна.

5.8. ЧМ сигнал длины

содержит

NM 

частот. Чипы с различными частотами

ортогональны. Возможно ли, чтобы АКФ данного сигнала имела нулевые значения при

всех ненулевых сдвигах вида

 m

148

6. Широкополосные сигналы для измерения времени,

синхронизации и разрешения во времени.

6.1. Дополнительные требования, предъявляемые к АКФ.

Вернемся к задачам оценивания временной задержки и разрешения во времени,

рассмотренным в 2.12, 2.15 и вспомним требования, предъявляемые к сигналу в случае,

когда требуются высокая точность измерения и разрешающая способность. В обеих этих

задачах необходимо выполнение следующего принципиального условия, заключающегося

в высокой концентрации во времени отклика согласованного фильтра на входной сигнал

или, что эквивалентно, «острой» АКФ сигнала, и тесно связанной с этим широкой полосы

сигнала. Привлекательность распределенности спектра в противовес простому укорачива-

нию сигнала состоит в том, что при значительном выигрыше от обработки

1WT

воз-

можно вложение в сигнал такого количества энергии, которое диктуется требуемой вели-

чиной отношения сигнал–шум (SNR), управляя только длительностью, а не пиковой мощ-

ностью, которая, как правило, жестко ограничена сверху. Тогда привлечение соответст-

вующей угловой модуляции позволяет расширить полосу сигнала, что обеспечит времен-

ную компрессию сигнала согласованным фильтром, так что длительность отклика фильт-

ра (время корреляции

/1

) окажется во много (примерно

)WT

раз меньше длитель-

ности

сигнала.

Уточним, какого вида АКФ можно считать «острой» или «хорошей», ориентируясь

на рассматриваемые задачи приема. Действительно, АКФ (см. определения (2.66) или

(2.67)) любого физически реализуемого сигнала не может строго равняться нулю при всех

значениях



, не принадлежащих интервалу

],[



, если время корреляции



меньше

длительности сигнала

. Тогда наряду с т. н. основным лепестком (main lobe), или цен-

тральным пиком (central peak), сосредоточенным в пределах интервала

],[



, АКФ

будет обладать также боковыми лепестками (side lobe), находящимися вне указанного ин-

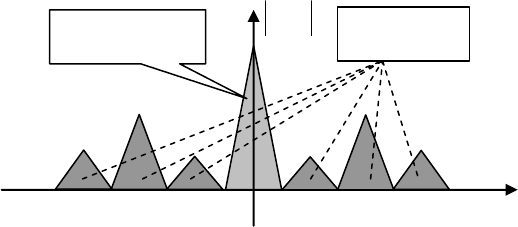
тервала (см. рис. 6.1). Наличие боковых лепестков носит преобладающе вредный харак-

тер, как при измерении запаздывания, так и разрешении во времени. Действительно, оп-

тимальное (по правилу максимального правдоподобия) измерение задержки сигнала тре-

бует фиксации временной позиции максимума огибающей выходного сигнала согласо-

ванного фильтра

)(tr

(см. параграф 2.12), а в отсутствии шума отклик согласованного

фильтра–детектора на входной сигнал в точности представляет собой АКФ огибающей. В

реальной ситуации, когда сигнал наблюдается на фоне шума, всегда имеется вероятность

возникновения ложного максимума вне «тела» основного пика АКФ, превышающего по

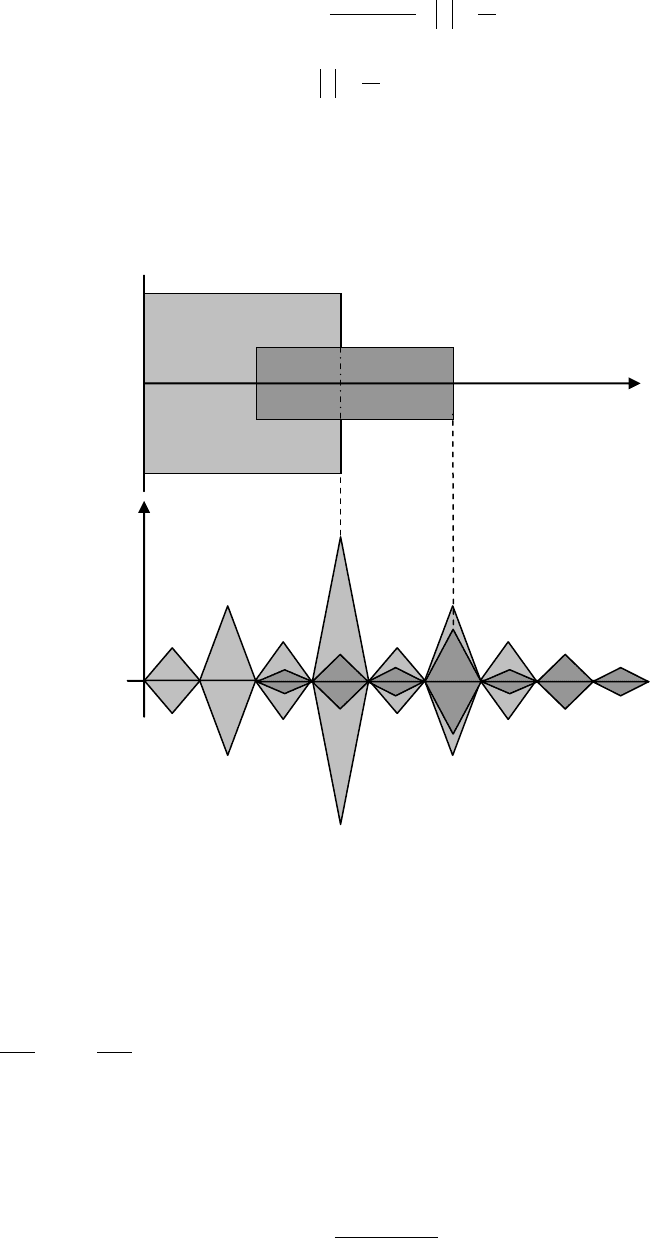
величине истинный (т.е. расположенный в пределах «тела»), что изображено пунктирной

линией на рис.6.2. В подобной ситуации возникает аномальная ошибка оценивания, при

Рис. 6.1. Основной пик и боковые лепестки АКФ.





)(R



Основной пик

Боковые

лепестки

149

которой отклонение



оценки



от истинного значения



превосходит



. Ясно, что пе-

репутывание основного лепестка с ложным пиком, возникающим поблизости от значи-

тельного бокового лепестка, более вероятно, чем с ложным пиком, возникающим «на пус-

том месте», поскольку для гауссовского шума «легче» поднять боковой лепесток до высо-

ты основного, чем создать его с нулевого уровня.

Для иллюстрации вредного влияния боковых лепестков на процедуру временного

разрешения рассмотрим суперпозицию двух копий полосного сигнала, которые характе-

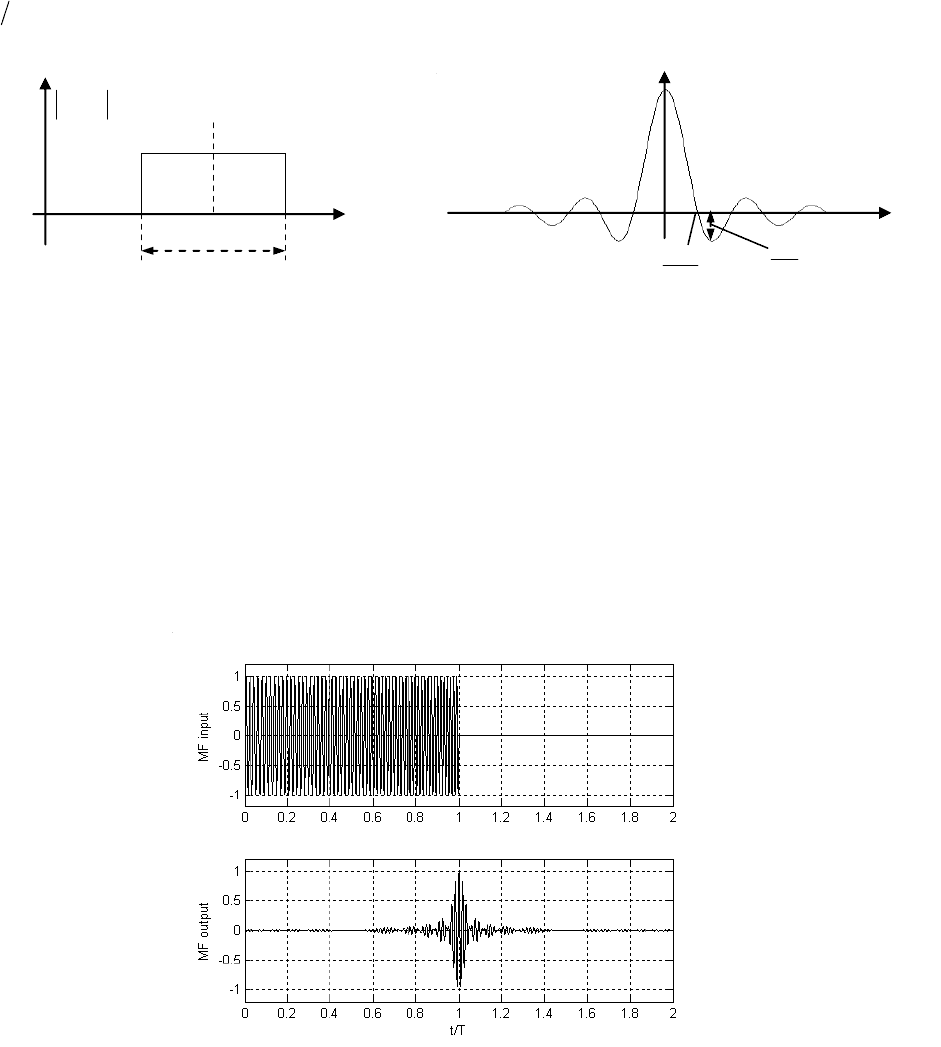
ризуется разными амплитудами и временными сдвигами, как это показано на рис. 6.3, а.

После обработки согласованным фильтром основной лепесток более слабой копии оказы-

вается полностью замаскированным боковым лепестком более сильной копии (см. рис.

6.3, b). В этих условиях наблюдатель не сможет надежно извлечь необходимую информа-

цию из обоих сигнальных копий или даже определить число принятых копий. Ситуация

подобного рода типична для случая не разрешимых сигналов, несмотря на то, что основ-

ной лепесток АКФ значительно уже длительности сигнала.

В наиболее общих терминах требования, предъявляемые широкополосным сигна-

лам при решении задач измерения запаздывания и разрешения во времени, теперь могут

быть сформулированы следующим образом: АКФ сигнала должна иметь достаточно

острый центральный пик и по возможности наиболее низкий уровень боковых лепестков.

В следующих параграфах этой главы будут рассмотрены пути и инструменты достижения

этой поставленной фундаментальной задачи.

6.2. Сигналы с непрерывной частотной модуляцией.

Исторически к числу первых открытых сигналов, обладающих эффектом времен-

ной компрессии согласованным фильтром, относится импульсный сигнал с линейной час-

тотной модуляцией (ЛЧМ). Как следует из названия, мгновенная частота этого сигнала

линейно изменяется в течение его длительности. Рассмотрим полосный сигнал, мгновен-

ная частота

)(tf

которого возрастает во времени по закону

,)(

ftf



где

– девиация частоты, т.е. полный диапазон изменения частоты, а

– как обычно,

центральная частота. Полная мгновенная фаза

)(t

сигнала определяется как интеграл от

мгновенной частоты и, следовательно, фаза ЛЧМ импульса подчиняется квадратичному

закону

,2)(2)(

tfduuft









Рис. 6.2. Иллюстрация возникновения аномальной ошибки.

)(

150

Полагая вещественную огибающую прямоугольной, комплексная огибающая ЛЧМ сигна-

ла принимает вид































,exp

)(

tWj



Подставляя это соотношение в общую формулу (2.66) для АКФ, последняя может быть

вычислена формально без особых трудностей. Однако существует менее формальный и

более прозрачный с физической точки зрения способ, приводящий к тому же результату.

Из теории частотной модуляции хорошо известно, что если индекс модуляции



значителен

)1( tW

, то спектр частотно-модулированного колебания содержит компо-

ненты всех мгновенных частот, причем форма спектра описывается вещественной оги-

бающей сигнала. Таким образом, в рассматриваемом случае спектр располагается в диапа-

зоне

]

[

f 

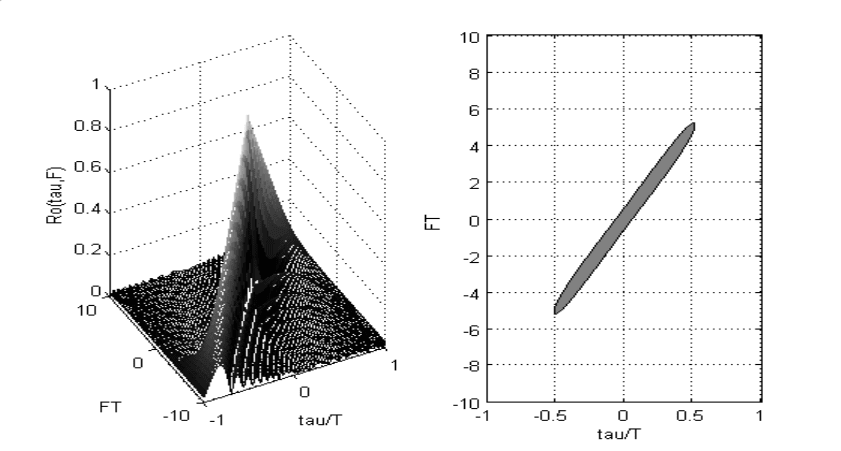
и имеет форму, близкую к прямоугольной (см. рис. 6.4, a). Те-

перь АКФ (2.66) может быть найдена в результате обратного преобразования Фурье, по-

добно тому, как это уже использовалось в 2.12.2. Поскольку энергетический спектр ока-

зывается прямоугольным, то его обратное преобразование Фурье даст функцию вида

xx/sin

, так что нормированная АКФ ЛЧМ сигнала представима как





W )sin(

)(



, (6.1)

что и демонстрирует рис. 6.4, b.

Как следует из рис. 6.4, полная (т.е. измеренная между двумя ближайшими к нача-

Рис. 6.3. Иллюстрация отсутствия разрешения сигналов.

)(r

)(ts

)( ts

151

лу координат нулями) ширина основного лепестка АКФ составляет

W/22 

. Тогда,

полагая ширину основного лепестка на некотором ненулевом уровне равной

W/1

получаем, что согласованный фильтр осуществляет временную компрессию ЛЧМ сигнала

WTTWT

/

раз.

Существенным недостатком ЛЧМ сигнала является высокий уровень боковых ле-

пестков АКФ. Ближайший к началу координат боковой лепесток имеет уровень, равный

)дБ13(21.032 

по отношению к основному, и не зависит от выигрыша от обработки

, т.е. он не может быть уменьшен за счет увеличения девиации

. Известны эффек-

тивные методы снижение уровня боковых лепестков путем сглаживания огибающей сиг-

нала либо использованием взвешивания, либо рассогласованной обработкой в приемнике.

Однако выигрыш в уровне боковых лепестков, достигаемый данными методами, обеспе-

чивается или за счет расширения основного пика, и/или потерями в отношении сигнал–

шум.

Пример 6.2.1. Рассмотрим прямоугольный ЛЧМ импульс с девиацией

/20

На рис. 6.5 представлены собственно сигнал и отклик на него согласованного фильтра,

полученные с использованием программы, разработанной в среде Matlab. Сравнение ве-

личины временной компрессии и уровня первого бокового лепестка с теоретически пред-

сказанными значениями показывают их практическое совпадение. 

Другим недостатком ЛЧМ сигнала является гребенчатая форма функции неопреде-

ленности

),(

F

. Из материала, изложенного в 2.14-2.15, можно сделать вывод о том,

)(

)(





3

Рис. 6.4. Аппроксимация спектра и АКФ ЛЧМ импульса.

Рис. 6.5 Временная компрессия прямоугольного ЛЧМ импульса.

152

что для одновременного измерения временной задержки и частоты точно также, как и для

частотно–временного разрешения наилучшей является игольчатая функция неопределен-

ности, обладающая одним центральным пиком в начале координат и резко спадающая во

всех направлениях частотно-временной плоскости. Как следует из рис. 6.6, на котором

изображены функция неопределенности (a) и диаграмма неопределенности (b) ЛЧМ сиг-

нала, последний не может служить эффективным инструментом для решения упомянутых

выше задач. Если пара значений

F,

попадает в эллипс, изображенный на рис. 6.6, b, точ-

ность оценивания этих параметров становится очень низкой, поскольку копии сигнала со

всеми подобными парами значений сильно коррелированны, т.е. с трудом поддаются раз-

личению. Аналогичный вывод можно сделать о разрешении таких сдвинутых по времени

и частоте копий сигнала: высокая схожесть делает задачу их разделения весьма проблема-

тичной.

Известны несколько способов улучшения формы функции неопределенности час-

тотно–модулированных сигналов, например, применение симметричной (V-типа) линей-

ной модуляции.

До сих пор непрерывные ЛЧМ сигнала и их модификации находят широкое приме-

нение в разнообразных широкополосных радарных и сонарных системах, однако в совре-

менных коммерческих коммуникационных системах или общедоступных системах даль-

ней навигации они не нашли широкого применения, уступая указанное пространство дис-

кретным сигналам. Одной из причин подобного предпочтения в дополнении к тому, о чем

уже упоминалось, может служить лучшая совместимость дискретных сигналов с совре-

менными цифровыми технологиями, микроэлектроникой и программно ориентированной

философией современных радиосистем.

6.3. Критерий выбора АФМ сигналов с хорошей апериодической АКФ.

Обратимся вновь к соотношению (5.5) и вспомним, что АКФ

)(



АФМ сигнала

представляет собой АФМ сигнал, у которого в качестве чипов выступает АКФ

)(



ис-

ходного элементарного импульса, а роль кодовой последовательности выполняет АКФ

Рис. 6.6 Функция неопределенности (a) и ее горизонтальное сечение (b) ЛЧМ сигнала.

153

)(m

исходного кода

110

,,,

N

aaa 

. Подобная конструкция явным образом свидетельст-

вует, что при заданном чипе профиль полной АКФ полностью определяется АКФ

)(m

кода. В частности, если длительность чипа не превышает периода их повторения

)( 

то «высота»

)(  m



любого бокового лепестка в точке

 m

просто повторяет величину

АКФ кода

)(m

при сдвиге на

позиций. Из установленного в 6.1 факта следует, что

минимизация уровня боковых лепестков АКФ имеет наивысший приоритет при конструи-

ровании сигнала всякий раз, когда одним из предназначений системы является измерение

времени запаздывания или временное разрешение. Конечно, было бы замечательно иметь

все боковые лепестки равными нулю, однако это абсолютно невозможно для финитных

или апериодических АФМ сигналов. Действительно, рассмотрим некоторый сигнал ко-

нечной длины

, что влечет выполнение неравенств

a



N

, поскольку в про-

тивном случае длина сигнала была бы меньше

. Тогда крайний правый боковой лепе-

сток нормированной апериодической АКФ кода (5.10) подобного сигнала будет

0)1(





. (6.2)

Последнее соотношение немедленно ведет к применению минимаксного критерия

при синтезе сигналов, который требует достижения минимально возможной величины

максимального бокового лепестка АКФ апериодического кода. Формальная запись данно-

го критерия имеет следующий вид

min})({max

max,





. (6.3)

В свете критерия (6.3) предпочтительными являются кодовые последовательности

с наименьшим значением максимального бокового лепестка, однако это требование всегда

сопровождается ограничением на метод модуляции или, более конкретно, на алфавит, ко-

торому принадлежат символы кодовой последовательности. Это ограничение отражает

технологические аспекты, касающиеся сложности формирования и обработки сигнала, и,

как вскоре станет явным, может оказаться очень обязывающим. Таким образом требова-

ния, предъявляемые к наилучшему сигналу, могут быть сформулированы в виде следую-

щей оптимизационной задачи: на множестве всех возможных последовательностей дли-

ны

с символами из заранее выбранного алфавиты найти последовательность или по-

следовательности с минимальной величиной максимального бокового лепестка апериоди-

ческой АКФ.

6.4. Об оптимизации апериодических АФМ сигналов.

Сформулированная выше оптимизационная задача, как и многие другие задачи

дискретной оптимизации, не имеют некоторого общего аналитического решения, и ти-

пичной процедурой ее выполнения является осуществление исчерпывающего поиска. Ог-

раничимся классом ФМ сигналов, общепризнанных наиболее привлекательными. В каче-

стве объяснения причин подобного утверждения достаточно напомнить, что в задачах

временного измерения и разрешения во времени основное достоинство широкополосно-

сти состоит в возможности распределения энергии сигнала на значительном временном

интервале, тем самым, снижая пиковую мощность. Сигналы с ФМ, свободные от ампли-

тудной модуляции, представляют собой предельную версию такого расширения, позво-

ляющую получить пик-фактор



сигнала (отношение пиковой к средней мощности), рав-

ный единице.

Для любого ФМ сигнала

1,,1,0,1  Nia



, так что



N

, и крайний пра-

154

вый боковой лепесток апериодической АКФ (6.2)

/1)1( 

. Следовательно, мак-

симальный боковой лепесток ФМ сигнала ограничен снизу величиной

max,



. (6.4)

Естественно, что ФМ сигналы, удовлетворяющие данной границе, будут оптимальными.

В честь ученого, первым предпринявшего поиск подобных сигналов, они получили назва-

ние кодов Баркера. Действительно, Баркеру удалось найти оптимальные бинарные коды,

лежащие на границе (6.4). Традиционно бинарные последовательности с символами

1

считаются наиболее привлекательными, поскольку в наибольшей степени отвечают циф-

ровой схемотехники и гарантируют наименьшую сложность в их формировании и обра-

ботки. В таблице 6.1 представлены все бинарные коды Баркера. Некоторые из кодов не

являются уникальными в том смысле, что существуют другие последовательности той же

длины, удовлетворяющие нижней границе (6.4).

Таблица 6.1. Бинарные коды Баркера.

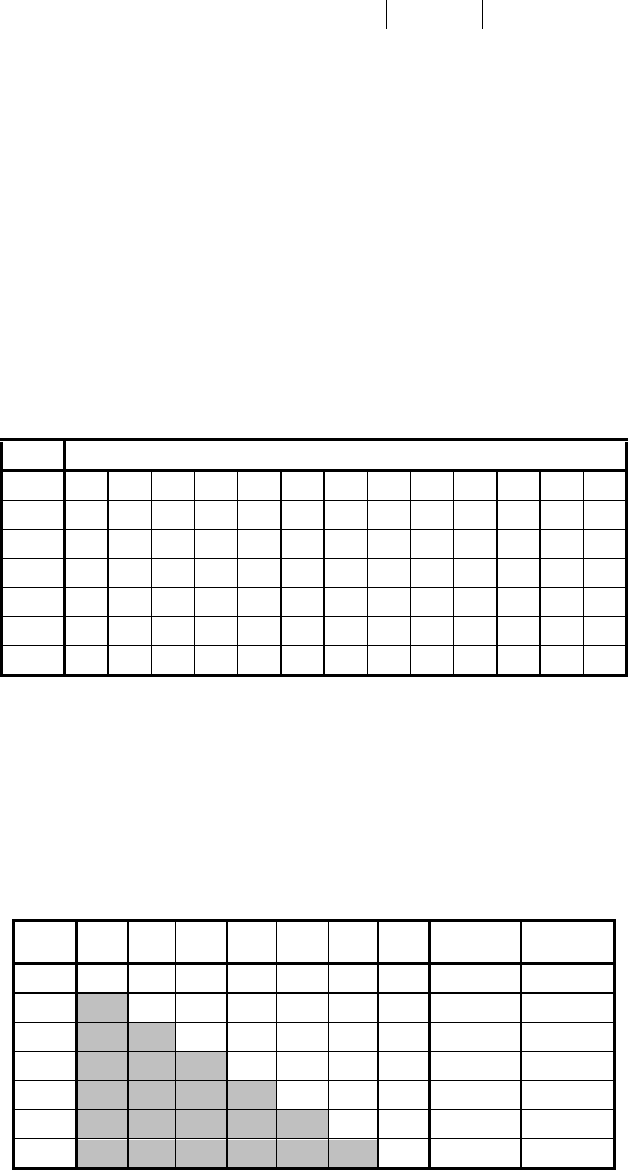
Пример 6.4.1. Таблица 6.2 иллюстрирует вычисление апериодической и периоди-

ческой АКФ кода Баркера длины

7N

. Структура таблицы полностью аналогична таб-

лице 5.1. Как видно, не только апериодическая, но и нормированная периодическая АКФ

характеризуется максимальным боковым лепестком, равным

N/1

. 

Таблица 6.2. Вычисление АКФ бинарного кода Баркера длины 7.

)(mR

–

–1

–

–1

–

–1

–

–1

–

–0

–1

–

–1

Рассмотрим кратко процедуру согласованной фильтрации сигнала Баркера на неко-

тором конкретном примере.

Пример 6.4.2. На рис. 6.7 изображена структура согласованного фильтра для сиг-

нала Баркера длины

7N

. Первым блоком данной структуры является линия задержки с

отводами, разделенными во времени на величину, равную периоду следования чипов



Выходные сигналы отводов линии задержки подаются на сумматор с весами, определяе-

мыми как зеркальное отражение символов кода. Второй частью структуры служит фильтр,

согласованный с одиночным чипом (СФОИ). Чтобы убедиться в том, что указанная схема

является искомым согласованным фильтром, достаточно осуществить проверку, подав на

Код

–

155

ее вход дельта–импульс. Выходной отклик представит собой зеркальное отображение

сигнала, что в точности соответствует реакции согласованного фильтра.

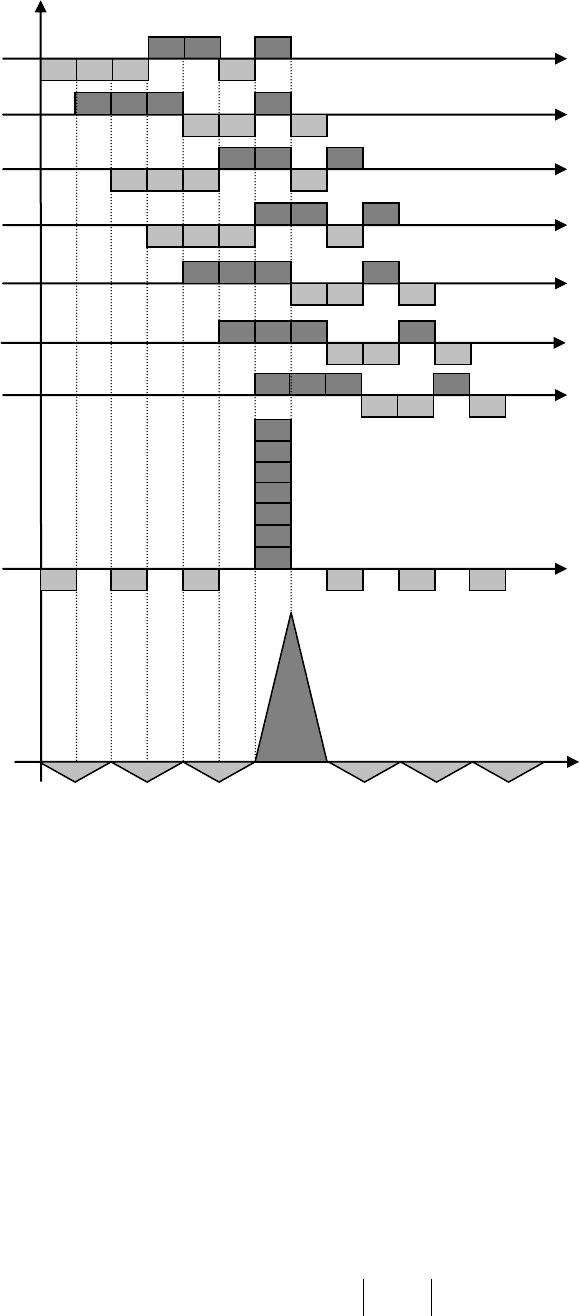
На рис.6.8 представлены диаграммы, пронумерованные в соответствие с точками

схемы, изображенной на рис. 6.7, которые иллюстрируют в деталях согласованную

фильтрацию видеосигнала Баркера, составленного из чипов с прямоугольной огибающей.

Когда последний чип сигнала поступит на вход фильтра, все предшествующие чипы поя-

вятся на входах сумматора с соответственно измененными полярностями и суммирование

осуществляется в фазе, обеспечивая получение основного пика АКФ. До этого момента и

после получаем боковые лепестки, имеющие полярность и уровень относительно основ-

ного в соответствие с результатами таблицы 6.2. 

К сожалению, бинарные коды Баркера существуют только для длин, приведенных в

таблице 6.1. Еще в 60–х годах Турин и Сторер доказали их не существование для любых

других нечетных длинах и для четных, по крайней мере из диапазона

121004  N

. Бы-

ли предприняты достаточно обширные исследования по поиску небинарных ФМ кодов

Баркера с эквидистантным фазовым алфавитом (многофазные или М–ичные ФМ коды),

однако достигнутые результаты далеки от обнадеживающих. Было обнаружено, что даже

скромные успехи в увеличении длины достигаются только за счет значительного увеличе-

ния размера

фазового алфавита. Возможно, что известные к настоящему времени мно-

гофазные коды Баркера наибольшей длины и найденные путем стохастического поиска

характеризуются объемами фазового алфавита от сотен до десятков тысяч

)3632( N

[23], или 60, 90, 120

)4537( N

[24]. Большой размер алфавита неизбежно влечет серь-

езные затруднения при аппаратной реализации, а также значительно более жесткие и

трудновыполнимые требования к допустимым ошибкам воспроизведения, дрейфу пара-

метров и т.п.

Как видно, длины существующих кодов Баркера достаточно малы для удовлетво-

рения многочисленных практических нужд, что в значительной степени стимулирует по-

иск бинарных последовательностей большей длины с уровнем боковых лепестков, пре-

вышающих нижнюю границу (6.4). Поскольку ненормированная АКФ (5.9) любой бинар-

ной последовательности всегда определяется суммой

1

, то возможные значения

max,a



для не баркеровких кодов принадлежат множеству

,/3,/2 NN

. Гарантированное на-

хождение глобально оптимального (т.е. имеющего минимально возможное

max,



при заданном

) бинарного кода может быть осуществлено только путем полного пере-

бора возможных комбинаций. К сожалению, вычислительный объем, необходимый для

подобной оптимизации, экспоненциально возрастает с увеличением длины

и становит-

ся не реализуемым при величинах

, превышающих 50. По крайней мере, как известно

автору, глобально оптимальные бинарные коды, открытые к настоящему времени, охва-

тывают диапазон вплоть до 50 [25, 26].

В соответствие с результатами [22] этот диапазон увеличен теперь до 1 898 884 и маловероятно, что би-

нарные коды Баркера четной длины существуют вне указанного диапазона.



)(ts

Вых

СФОИ

–

Рис. 6.7. Согласованный фильтр для бинарного сигнала Баркера длины N=7.

156

Если основываться на факте, что нахождение глобально оптимальных бинарных

последовательностей большой длины практически не реализуемо, задача (6.3) может быть

сформулирована в более ограниченном виде: найти бинарный код с удовлетворительно

малым уровнем апериодического бокового лепестка

max,a



без гарантии глобальной оп-

тимальности. Общая идея алгоритмов, направленных на решение этой задачи, состоит в

предварительном отборе некоторого ограниченного множества последовательностей, ко-

торое кажется многообещающим в плане корреляционных свойств, и последующем скру-

пулезном поиске кода с минимальным значением

max,a



только среди последовательно-

стей, вошедших в указанное множество. Одним из примеров подобной стратегии является

эволюционный алгоритм [27], посредством которого были найдены бинарные коды длин

до ста включительно, некоторые из которых незначительно лучше кодов Баркера. Так, для

кода Баркера длины 13

077.013/1

max,



, а для лучшего в смысле

max,a



кода из [27]

068.088/6

max,



. Другой продуктивный поход основан на соотношении (5.13), свя-

зывающем апериодическую АКФ со своим периодическим аналогом. Обозначая через

max,p



, максимальный боковой лепесток периодической АКФ

})({max

1,2,1

max,



 

Рис.6.8 Согласованная фильтрация бинарного сигнала Баркера длины N=7.