Хлыбов А.А., Хлыбова О.Н. MathCAD и MATLAB Начальный курс Учебно-методическое пособие

Подождите немного. Документ загружается.

Глава 1. MathCAD

1.2.2. Построение трехмерных графиков

Трехмерные, или 3D-графики, отображают функции двух переменных

вида Z(X, Y).

Такие графики можно построить несколькими способами:

• применить встроенную функцию MathCAD

CreateMesh

CreateMesh(F, x0, x1, y0, y1, xgrid, ygrid, fmap) создает сетку на

поверхности, определенной функцией F, x0, x1, y0, y1 – диапазон изменения

переменных,

xgrid, ygrid – размеры сетки переменных, fmap – функция

отображения. По умолчанию

CreateMesh создает сетку на поверхности с

диапазоном изменения переменных от –5 до 5 и с сеткой 20×20 точек.

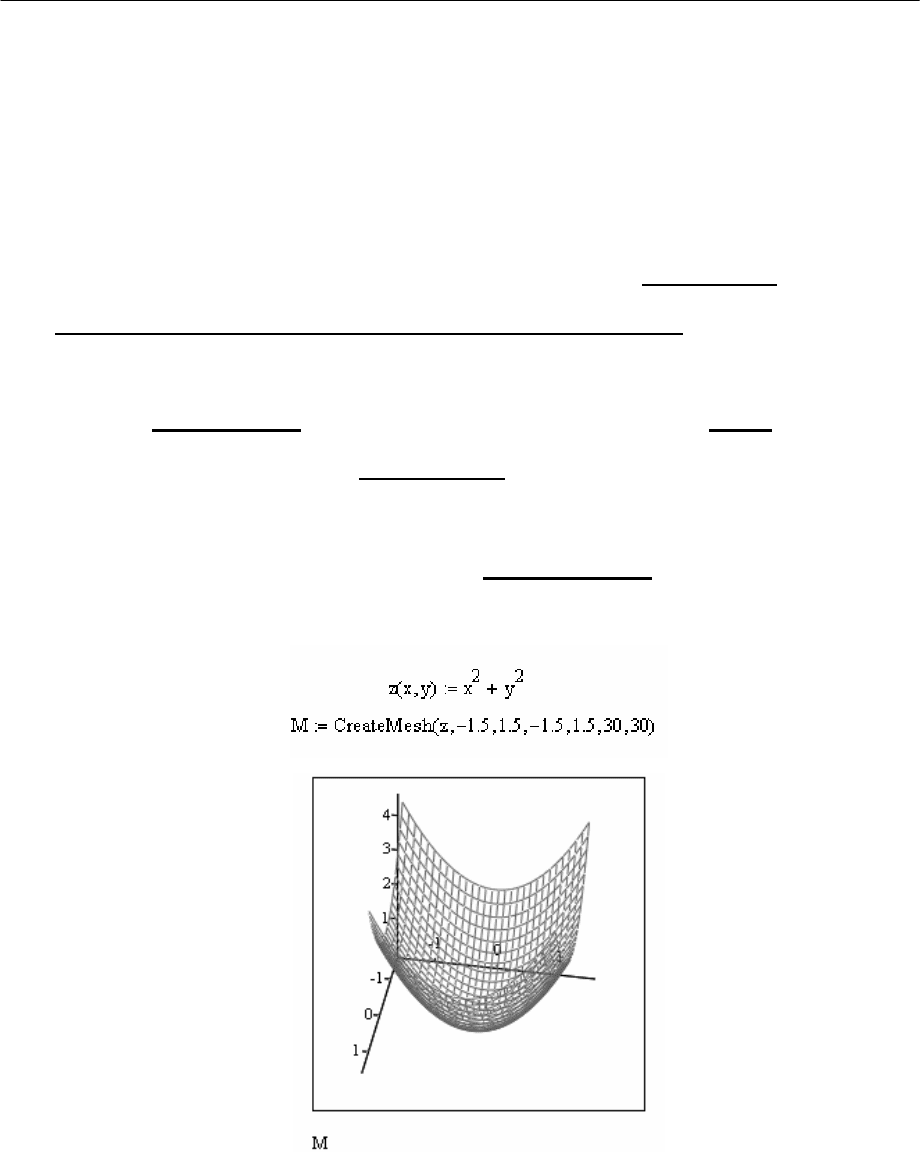
Пример использования функции

CreateMesh для построения 3D-

графиков приведен на Рис. 3.

Рис.1.3

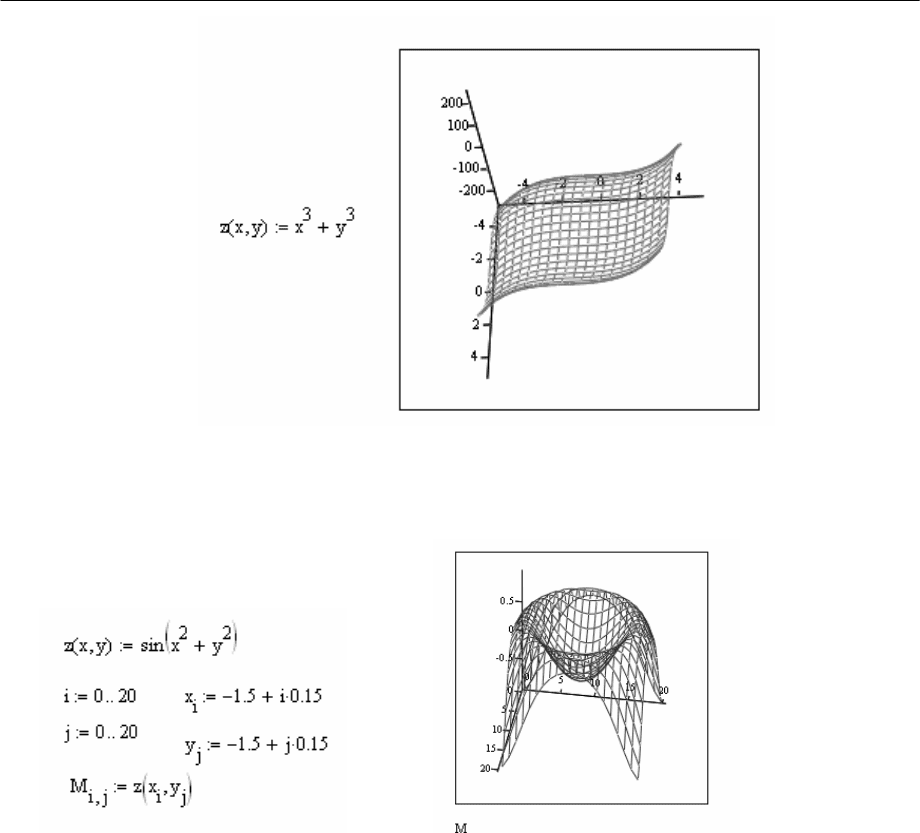
• быстрое создание графика

Для «быстрого» создания трехмерных графиков необходимо в

местозаполнитель ввести имя функции от двух переменных (Рис.1.4).

Глава 1. MathCAD

Рис. 1.4

• дискретизация значений функции

Рис. 1.5

1.2.3. Построение пересекающихся фигур

Особый интерес представляет собой возможность построения на одном

графике ряда разных фигур или поверхностей с автоматическим учетом их

взаимного пересечения. Для этого надо раздельно задать матрицы

соответствующих поверхностей и после вывода шаблона 3D-графика

перечислить эти матрицы под ним с использованием в качестве разделителя

запятой (Рис. 1.6).

Глава 1. MathCAD

fxy,()sinx

(

)

:= gxy,()x

+ 6−:= x020..:= y0

..:=

xy,

x10−()

y10−()

⎡

⎢

⎣

⎤

⎥

⎦

:= L

xy,

x6−()

y6−()

⎡

⎢

⎣

⎤

⎥

⎦

ML, L,

Рис. 1.6. Построение двух пересекающихся поверхностей.

1.2.4. Форматирование графиков

Форматирование двухмерных графиков происходит в окне

Форматирование осей включает в себя управление их внешним

видом, диапазоном, шкалой, нумерацией и отображением некоторых

значений на осях при помощи маркеров.

Изменение внешнего вида шкалы, нанесенной на координатную ось,

производится с помощью диалогового окна Форматирование выбранного

графика (Formatting Currently Selected X-Y Plot). Вызвать его можно

двойным щелчком в области графика или Формат ⇒График ⇒Точка Х-У.

Глава 1. MathCAD

С помощью флажков и переключателей легко поменять внешний вид

каждой из осей. Доступные опции:

- логарифмический масштаб; удобен, если данные разнятся на

несколько порядков.

- линии сетки;

- нумерация, если убрать этот флажок, то числа, размечающие шкалу,

пропадут.

- автомасштаб.

- показать метки, после включения этой опции надо в появившиеся

местозаполнители ввести числи или имя переменной, значение которой вы

хотите отобразить на оси маркером.

- равные масштабы, оси ОХ и ОУ принудительно рисуются в

одинаковом масштабе.

- стиль осей графика можно выбрать из трех видов: ограниченная

область- прямоугольник; пересечение – оси в виде двух пересекающихся

прямых; без границ – оси не показываются на графике.

С помощью вкладки Traces (Трассировки) можно выбрать вид линий.

Здесь же регулируются следующие параметры:

- легенда, описывает ряд данных,

- символ, вид маркера, которым обозначаются отдельные точки

данных,

- строка: solid-сплошная, dot-пунктир, dash-штрих, dadot-штрих-

пунктир,

- цвет линий и точек данных,

- тип представления ряда данных: lines (линии), points (точки), error

(ошибки), bar (столбцы), step (шаг), draw (рисунок), stem (стержень), solid bar

(гистограмма),

- вес – толщина линии.

Тип графика с отображением погрешностей (ошибок) требует задания

трех серий данных. Помимо пар (ХУ) необходимо задать еще две

Глава 1. MathCAD

последовательности данных, представляющих соответствующие значения

ошибок для каждой пары точек.

Для некоторых типов графиков те или иные параметры недоступны,

например, нельзя задать символ для шаговой кривой.

Создать заголовок графика можно на вкладке Метки.

Форматирование трехмерных графиков выполняется с помощью

диалогового окна Формат 3-D графика, которое вызывается двойным

щелчком мыши в области графика.

Изменение типа и масштаба графика происходит на вкладке Общее.

Вращение графика с нажатой левой кнопкой мыши – самый простой способ

ориентации системы координат. Другой способ изменения ориентации – с

помощью полей Вращение, Наклон, Поворот на вкладке Общие, которые в

совокупности определяют соответствующие углы в градусах, и тем самым

задают направление всех осей координат в пространстве. Вкладка Оси

содержит три вложенных вкладки, в которых задаются параметры для

каждой из трех осей. Можно включить или отключить показ линий сетки,

нумерации, задать диапазон по каждой из осей. При помощи вкладки Задние

планы задается показ проекций координатной сетки на три скрытые

плоскости трехмерного графика. На вкладке Дополнительно можно задать

Туман, Прозрачность, Перспективу, Блеск, Подсветку.

Глава 1. MathCAD

1.2.5. Создание анимационного клипа

Основной принцип анимации в MathCAD – покадровая анимация.

Номер кадра задается переменной FRAME.

Алгоритм создания анимационного клипа:

• Создайте объект, чей вид зависит от FRAME.

• Убедитесь, что установлен режим автоматического расчета

(Математика ⇒ Автоматическое Вычисление).

• Выберите Вид

→ Анимация для вызова одноименного

диалогового окна;

• Заключите в выделяющий пунктирный прямоугольник часть

рабочего документа, которую нужно анимировать;

• Установите нижние и верхние границы FRAME (поля От: и До:);

• В поле Скорость введите значение скорости воспроизведения

(кадров/сек);

• Выберите Анимация. После этого в окошке диалогового окна

Анимация будут появляться результаты расчетов выделенной области. По

окончании этого процесса на экране появится окно проигрывателя анимации;

• Запустите просмотр анимации;

• Сохраните анимацию как АVI файл, нажав на кнопку Сохранить

как в окне Анимация;

• Воспроизведите сохраненную анимацию Вид

⇒Воспроизведение.

Сохраненный видеофайл можно использовать за пределами MathCAD.

1.3. Решение уравнений и систем уравнений средствами

MathCAD

Как известно, многие уравнения и системы уравнений не имеют

аналитических решений. В первую очередь это относится к большинству

трансцендентных уравнений. Доказано также, что нельзя построить формулу,

Глава 1. MathCAD

по которой можно было бы решить произвольное алгебраическое уравнение

степени выше четвертой. Однако такие уравнения могут решаться

численными методами с заданной точностью (не более значения заданного

системной переменной TOL).

1.3.1. Численное решение алгебраического уравнения

Рассмотрим одно алгебраическое уравнение с одним неизвестным,

f(x)=0. Для решения таких уравнений MathCAD имеет встроенную функцию

root, которая, в зависимости от типа задачи, может включать либо два, либо

четыре аргумента root(f(x),x) и root(f(x),x,a,b);

где f(x) – скалярная функция, определяющая уравнение, х – скалярная

переменная, относительно которой решается уравнение, a,b – границы

интервала, внутри которого происходит поиск корня.

Первый тип функции root требует дополнительного задания

начального значения переменной х. Поиск корня будет производиться вблизи

этого значения. Таким образом, присвоение начального значения требует

априорной информации о примерной локализации корня.

Начальные приближения могут быть:

1. Известны из физического смысла задачи.

2. Известны из решения аналогичной задачи при других исходных

данных.

3. Найдены графическим способом.

Наиболее распространен графический способ определения начальных

приближений. Принимая во внимание, что действительные корни уравнения

f(x) = 0 - это точки пересечения графика функции f(x) с осью абсцисс,

достаточно построить график функции f(x) и отметить точки пересечения f(x)

с осью Ох, или отметить на оси Ох отрезки, содержащие по одному корню.

Построение графиков часто удается сильно упростить, заменив

уравнение f(x) = 0 равносильным ему уравнением: f

(x)=f

(x), где функции

(x) и f

(x) - более простые, чем функция f(x). Тогда, построив графики

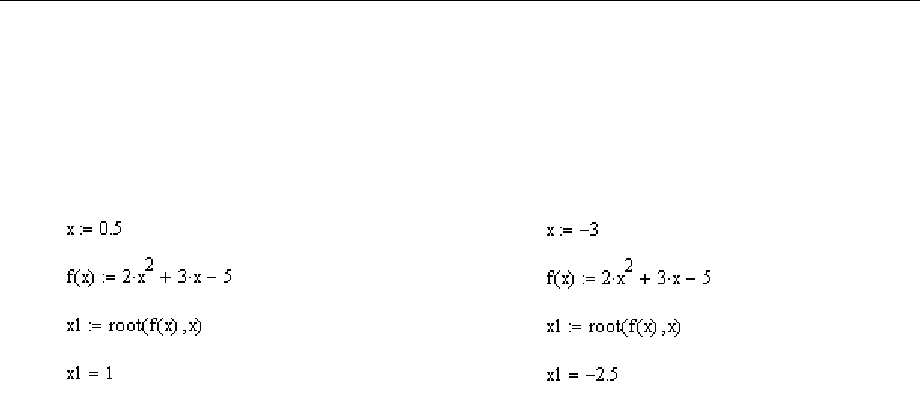
Глава 1. MathCAD

функций у = f

(x) и у = f

(x), искомые корни получим как абсциссы точек

пересечения этих графиков.

Пример решения уравнения с начальным приближением.

Найдем первый корень: Найдем второй корень:

Корни найдены при задании разных начальных приближений.

Отсутствие сходимости функции root

Если после многих итераций MathCAD не находит подходящего

приближения, то появится сообщение Can’t converge to a solution.

(отсутствует сходимость). Эта ошибка может быть вызвана следующими

причинами:

• Уравнение не имеет корней.

• Корни уравнения расположены далеко от начального приближения.

• Выражение имеет локальные max и min между начальным

приближением и корнями.

• Выражение имеет разрывы между начальными приближениями и

корнями.

• Выражение имеет комплексный корень, но начальное приближение

было вещественным.

Чтобы установить причину ошибки, исследуйте график f(x). Он

поможет выяснить наличие корней уравнения f(x) = 0 и, если они есть, то

определить приблизительно их значения. Чем точнее выбрано начальное

приближение корня, тем быстрее будет root сходиться.

Рекомендации по использованию функции root

• Для изменения точности, с которой функция root ищет корень,

нужно изменить значение системной переменной TOL. Если значение TOL

Глава 1. MathCAD

увеличивается, функция root будет сходиться быстрее, но ответ будет менее

точен. Если значение TOL уменьшается, то функция root будет сходиться

медленнее, но ответ будет более точен. Чтобы изменить значение TOL в

определенной точке рабочего документа, используйте определение вида

TOL=0.01. Чтобы изменить значение TOL для всего рабочего документа,

выберите команду Математика ⇒ Параметры… ⇒ Переменные ⇒

Допуск сходимости (TOL).

• Если два корня расположены близко друг от друга, следует

уменьшить TOL, чтобы различить их.

• Если функция f(x) имеет малый наклон около искомого корня,

функция root(f(x), x) может сходиться к значению k, отстоящему от корня

достаточно далеко. В таких случаях для нахождения более точного значения

корня необходимо уменьшить значение TOL. Другой вариант заключается в

замене уравнения f(x) = 0 на g(x) = 0

)(

xg =

• Для выражения f(x) с известным корнем “а” нахождение

дополнительных корней f(x) эквивалентно поиску корней уравнения

h(x) = f(x)/(x - a). Подобный прием полезен для нахождения корней,

расположенных близко друг к другу. Проще искать корень выражения h(x),

чем пробовать искать другой корень уравнения f(x) = 0, выбирая различные

начальные приближения.

1.3.2. Нахождение корней полинома

Если функция f(x) является полиномом v

+ ... + v

+ v

, то

все его корни можно определить, используя встроенную функцию

polyroots(v), где v-вектор, составленный из коэффициентов полинома. Так

как полином n-ой степени имеет ровно n корней (действительных и/или

комплексных, некоторые из них могут быть кратными), то вектор v должен

состоять из n+1 элемента. Результатом действия функции polyroots является

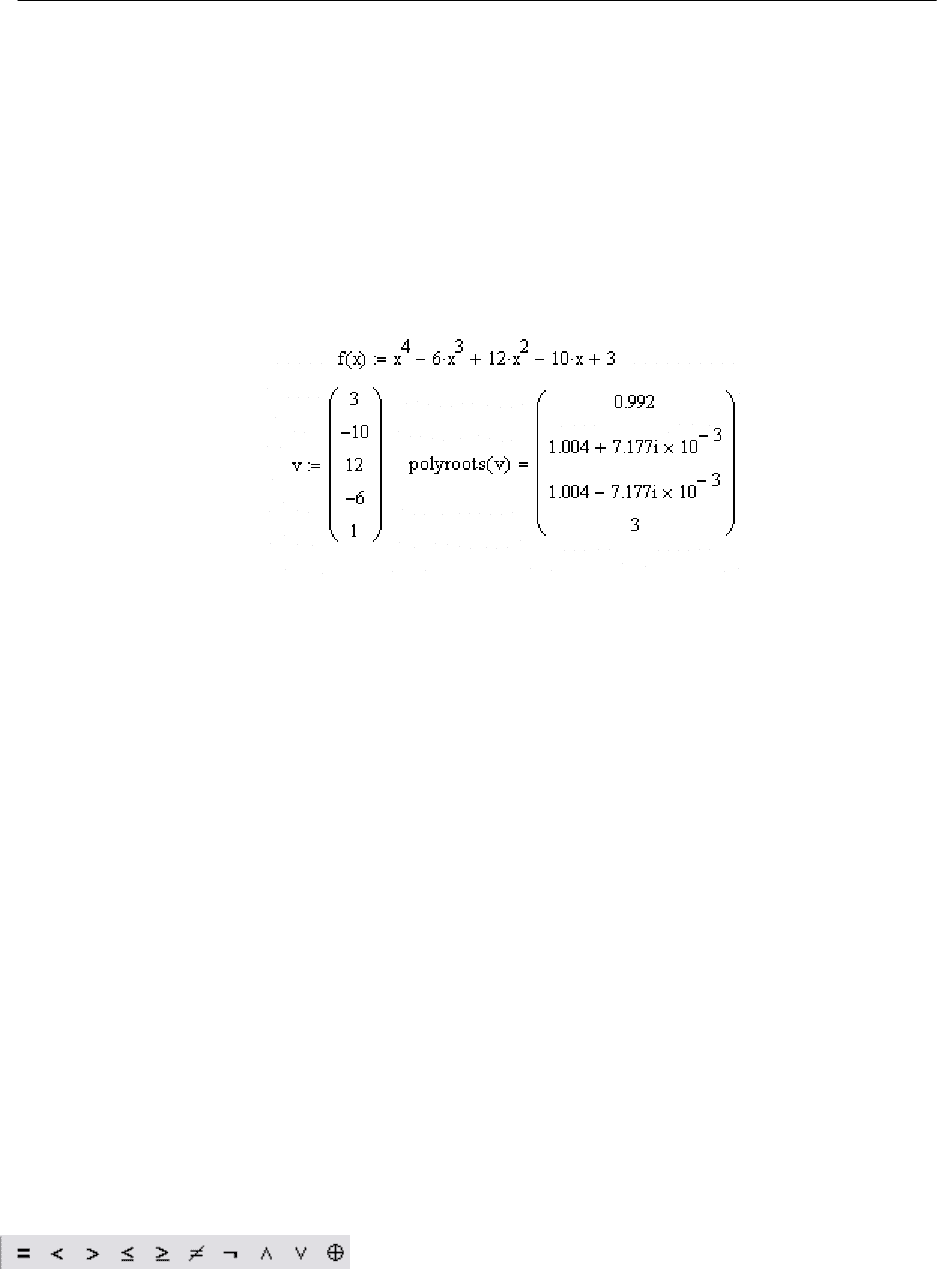
Глава 1. MathCAD

вектор, составленный из n корней рассматриваемого полинома. Начальное

приближение вводить не надо.

Вектор

v удобно создавать использую команду Символы ⇒

Коэффициенты полинома.

Следующий пример иллюстрирует определение корней полинома

средствами MathCAD:

1.3.3. Решение систем уравнений

MathCAD дает возможность решать также и системы уравнений

(линейные и нелинейные). Максимальное число уравнений и переменных

равно 50. Результатом решения системы будет численное значение искомого

корня.

Для решения систем имеется специальный вычислительный блок,

состоящий из трех частей, идущих последовательно друг за другом:

Given – ключевое слово;

Система, записанная логическими операторами в виде равенств или

неравенств;

Find(x

,…x

) – встроенная функция для решения системы

относительно переменных x

,…x

Вставлять логические операторы следует, пользуясь панелью Булевы

. Блок Given/ Find использует для поиска

решения итерационные методы, поэтому требуется задать начальные

значения для всех x

,…x

. Сделать это необходимо до ключевого слова

Given. Значение функции Find есть вектор, составленный из решения по