Хлыбов А.А., Хлыбова О.Н. MathCAD и MATLAB Начальный курс Учебно-методическое пособие

Подождите немного. Документ загружается.

Глава 2. MATLAB

Кроме того, имеются три утилиты, связанные с операциями над

объектами:

closereq — закрыть окно по запросу;

ishandle — проверить дескриптор на истинность;

newplot — восстановить свойства объекта, измененные nextPlot.

Назначение большинства этих операций достаточно очевидно.

2.3. Обработка данных

2.3.1. Статистическая обработка данных

Нахождение максимального и минимального элементов массива

Самый простой анализ данных, содержащихся в некотором массиве,

заключается в поиске его элементов с максимальным и минимальным

значениями. В системе MATLAB определены следующие быстрые функции

для нахождения минимальных и максимальных элементов массива:

• mах(А) — возвращает наибольший элемент, если А — вектор;

или возвращает вектор-строку, содержащую максимальные элементы

каждого столбца, если А — матрица, в многомерных массивах работает с

первой не единичной размерности;

• mах(А,В) — возвращает массив того же размера, что А и В,

каждый элемент которого есть максимальный из соответствующих элементов

этих массивов;

• max(A,[ ],dim) — возвращает наибольшие элементы по столбцам

или по строкам матрицы в зависимости от значения скаляра dim. Например,

тах(А,[ ],1) возвращает максимальные элементы каждого столбца матрицы А;

• [C,I] =max(A) — кроме максимальных значений возвращает

вектор индексов I этих элементов.

Примеры:

a=[1 2 3;4 5 1;6 7 2]; b=[2 7 6;8 5 9;3 4 6];

Глава 2. MATLAB

max(a)

ans =

6 7 3

max(a,b)

ans =

2 7 6

8 5 9

6 7 6

Для быстрого нахождения элемента массива с минимальным

значением служит следующая функция:

• min(A) — возвращает минимальный элемент, если А — вектор;

или возвращает вектор-строку, содержащую минимальные элементы каждого

столбца, если А — матрица;

• min(A,B) — возвращает массив того же размера, что А и В,

каждый элемент которого есть минимальный из соответствующих элементов

этих массивов;

• min(A,[ ],dim) — возвращает наименьший элемент по столбцам

или по строкам матрицы в зависимости от значения скаляра dim. Например,

mах(А,[ ],1) возвращает минимальные элементы каждого столбца матрицы А;

• [C,I] = min(A) — кроме минимальных значений возвращает

вектор индексов этих элементов.

Пример:

A=magic(4)

A =16 2 3 13

5 11 10 8

9 7 6 12

4 14 15 1

[C.I]=min(A)

C =

I: [4 2 3 1]

Работа указанных функций базируется на сравнении численных

значений элементов массива А, что и обеспечивает высокую скорость

выполнения операций.

Нахождение средних, срединных значений массива и стандартных

отклонений

Глава 2. MATLAB

Элементарная статистическая обработка данных в массиве обычно

сводится к нахождению их среднего значения, медианы (срединного

значения) и стандартного отклонения. Для этого в системе MATLAB

определены следующие функции:

• mean (А) — возвращает арифметическое среднее значение

элементов массива, если А — вектор; или возвращает вектор-строку,

содержащую средние значения элементов каждого столбца, если А —

матрица. Арифметическое среднее значение есть сумма элементов массива,

деленная на их число;

• mean(A,dim) — возвращает среднее значение элементов по

столбцам или по строкам матрицы в зависимости от значения скаляра dim

(dim=l по столбцам и dim=2 по строкам соответственно).

Примеры:

A=[1 4 3; 3 6 12; 8 11 9]

A =

1 4 3

3 6 12

8 11 9

b=mean(A)

b =

4 7 8

• median (A) — возвращает медиану, если А — вектор; или вектор-

строку медиан для каждого столбца, если А — матрица;

• median(A,dim) — возвращает значения медиан для столбцов или

строк матрицы в зависимости от значения скаляра dim.

Примеры:

A=magic(3)

A =

8 1 6

3 5 7

4 9 2

M=median(A)

M =

4 5 6

M=median(A,2)

M =

Глава 2. MATLAB

• std(X) — возвращает стандартное отклонение элементов массива,

если X — вектор. Если X — матрица, то std(X) возвращает вектор-строку,

содержащую стандартное отклонение элементов каждого столбца (обратите

внимание, что оно отличается от среднеквадратического отклонения);

• std(X.flag) — возвращает то же значение, что и std(X), если

flag=0; если flag=l, функция std(X.l) возвращает среднеквадратическое

отклонение (квадратный корень из несмещенной дисперсии);

• std(X.flag.dim) — возвращает стандартное или

среднеквадратическое отклонения по рядам (dim=2) или по столбцам(dim=1)

матрицы X в зависимости от значения переменной dim.

Примеры:

» X = linspace(0,3*pi,10)

X = Columns 1 through 7

0 1.0472 2.0944 3.1416 4.1888 5.2360 6.2832

Columns 8 through 10

7.3304 8.3776 9.4248

» s = std(X)

s =

3.1705

Функции сортировки элементов массива

Многие операции статистической обработки данных выполняются

быстрее и надежнее, если данные предварительно отсортированы. Кроме

того, нередко представление данных в отсортированном виде более наглядно

и ценно. Ряд функций служит для выполнения сортировки элементов

массива:

• sort (А) — в случае одномерного массива А сортирует и

возвращает элементы по возрастанию их значений; в случае двумерного

массива происходит сортировка и возврат элементов каждого столбца.

Допустимы вещественные, комплексные и строковые элементы. Если А

Глава 2. MATLAB

принимает комплексные значения, то элементы сначала сортируются по

абсолютному значению, а затем, если абсолютные значения равны, по

аргументу. Если А включает NaN-элементы, sort помещает их в конец;

• [В, INDEX] = sort(A) — наряду с отсортированным массивом

возвращает массив индексов INDEX. Он имеет размер size(A), с помощью

этого массива можно восстановить структуру исходного массива.

• sort(A,dim) — для матриц сортирует элементы по столбцам

(dim=l) или по рядам в зависимости от значения переменной dim.

Примеры:

A=magic(3)

A =

8 1 6

3 5 7

4 9 2

[B,INDEX]=sort(A)

B =

3 1 2

4 5 6

8 9 7

sort(A,2)

ans =

1 6 8

3 5 7

2 4 9

• sortrows(A) — выполняет сортировку рядов массива А по

возрастанию и возвращает отсортированный массив, который может быть

или матрицей, или вектором-столбцом;

• sortrows(A,column) — возвращает матрицу, отсортированную по

столбцам, точно указанным в векторе column. Например, sortrows(A,[2 3])

сортирует строки матрицы А сначала по второму столбцу, и затем, если его

элементы равны, по третьему;

• [В, index] = sortrows (А) — также возвращает вектор индексов

index. Если А — вектор-столбец, то B=A(index). Если А — матрица размера

m*n, то B=A(index.:).

B=[1 5 7; 8 12 4; 6 7 14]

B =

1 5 7

8 12 4

6 7 14

C=sortrows(B)

C =

1 5 7

6 7 14

d=sortrows(B,3)

d =

8 12 4

1 5 7

Глава 2. MATLAB

8 12 4 6 7 14

• cplxpair(A) — сортирует элементы по строкам или столбцам

комплексного массива А, группируя вместе комплексно сопряженные пары.

Затем найденные пары сортируются по возрастанию действительной части.

Внутри пары элемент с отрицательной мнимой частью является первым.

Действительные элементы следуют за комплексными парами. Заданный по

умолчанию порог 100*eps относительно abs(A(i))) определяет, какие числа

являются действительными и какие элементы являются комплексно

сопряженными. Если А — вектор, cpl xpair (А) возвращает А вместе с

комплексно сопряженными парами. Если А — матрица, cpl xpai r(А)

возвращает матрицу А с комплексно сопряженными парами, сортированную

по столбцам;

• cplxpalr(A,tol) — отменяет заданный по умолчанию порог и

задает новый tol;

• cplxpair(A.[],dim) — сортирует матрицу А по строкам или по

столбцам в зависимости от значения параметра dim;

• cplxpair(A,tol ,dim) — сортирует матрицу А по строкам или по

столбцам в зависимости от значения параметра dim, используя заданный

порог tol.

2.3.2. Интерполяция и аппроксимация данных

Под аппроксимацией обычно подразумевается описание некоторой,

порой не заданной явно, зависимости или совокупности представляющих ее

данных с помощью другой, обычно более простой или более единообразной

зависимости. Часто данные находятся в виде отдельных узловых точек,

координаты которых задаются таблицей данных. Результат аппроксимации

может не проходить через узловые точки.

Напротив, задача интерполяции — найти данные в окрестности

узловых точек. Для этого используются подходящие функции, значения

которых в узловых точках совпадают с координатами этих точек. Например,

Глава 2. MATLAB

при линейной интерполяции зависимости у(х) узловые точки соединяются

друг с другом отрезками прямых и считается, что искомые промежуточные

точки расположены на этих отрезках.

Для повышения точности интерполяции применяют параболы

(квадратичная интерполяция) или полиномы более высокой степени

(полиномиальная интерполяция). Для обработки данных MATLAB

использует различные функции интерполяции и аппроксимации данных.

Полиномиальная регрессия

Одна из наиболее известных аппроксимаций — полиномиальная. В

системе MATLAB определены функции аппроксимации данных полиномами

по методу наименьших квадратов — полиномиальной регрессии. Это

выполняет функция, приведенная ниже:

• polyfit(x,y,n) — возвращает вектор коэффициентов полинома р(х)

степени n, который с наименьшей среднеквадратичной погрешностью

аппроксимирует функцию у(х). Результатом является вектор-строка длиной

n+1, содержащий коэффициенты полинома в порядке уменьшения степеней х

и у;

• [p,S] = polyfit(x,y,n) — возвращает коэффициенты полинома р и

структуру S для использования вместе с функцией polyval с целью

оценивания или предсказания погрешности;

• [p,S] = polyfit(x,y,n,mu) возвращает коэффициенты полинома р и

структуру S для использования вместе с функцией polyval с целью

оценивания или предсказания погрешности, но так, что происходит

центрирование (нормирование) и масштабирование х, xnorm = (х -

mu(l))/mu(2), где mu(l) = mean(x) и mu(2) = std(x). Центрирование и

масштабирование не только улучшают свойства степенного многочлена,

получаемого при помощи polyval, но и значительно повышают качественные

характеристики самого алгоритма аппроксимации.

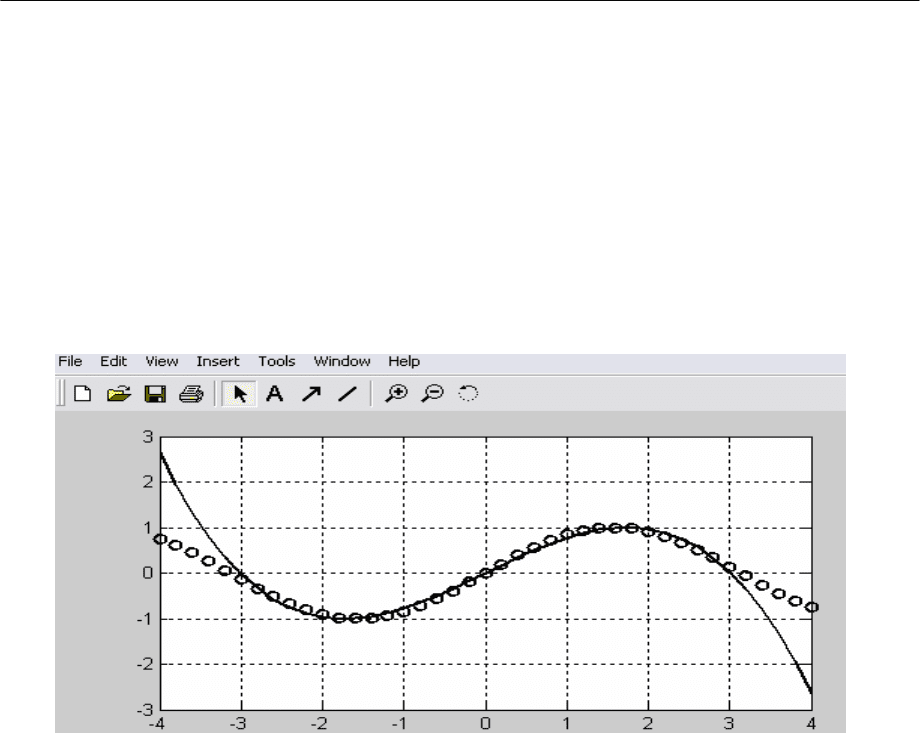
Пример: Полиномиальная регрессия для функции sin

x=(-3:0.2:3)';

Глава 2. MATLAB

y=sin(x);

p=polyfit(x,y,3)

p = -0.0953 -0.0000 0.8651 0.0000

x=(-4:0.2:4)';

y=sin(x);

f=polyval(p,x);

plot(x,y,'o',x,f)

Рисунок, построенный в этом примере, дает наглядное представление о

точности полиномиальной аппроксимации. Следует помнить, что она

достаточно точна в небольших окрестностях от точки х = 0, но может иметь

большие погрешности за их пределами или в промежутках между узловыми

точками.

График аппроксимирующего полинома третьей степени на рисунке

показан сплошной линией, а точки исходной зависимости обозначены

кружками. К сожалению, при степени полинома свыше 5 погрешность

полиномиальной регрессии (и аппроксимации) сильно возрастает и ее

применение без центрирования и масштабирования становится рискованным.

Обратите внимание на то, что при полиномиальной регрессии узловые точки

не ложатся точно на график полинома, поскольку их приближение к нему

является наилучшим в смысле минимального среднеквадратического

отклонения.

Глава 2. MATLAB

2.3.3. Обработка данных в графическом окне

В меню Tools имеются две команды для обработки данных:

Basic Fiting – основные виды аппроксимации (регрессии);

Data Statistics – статистические параметры данных.

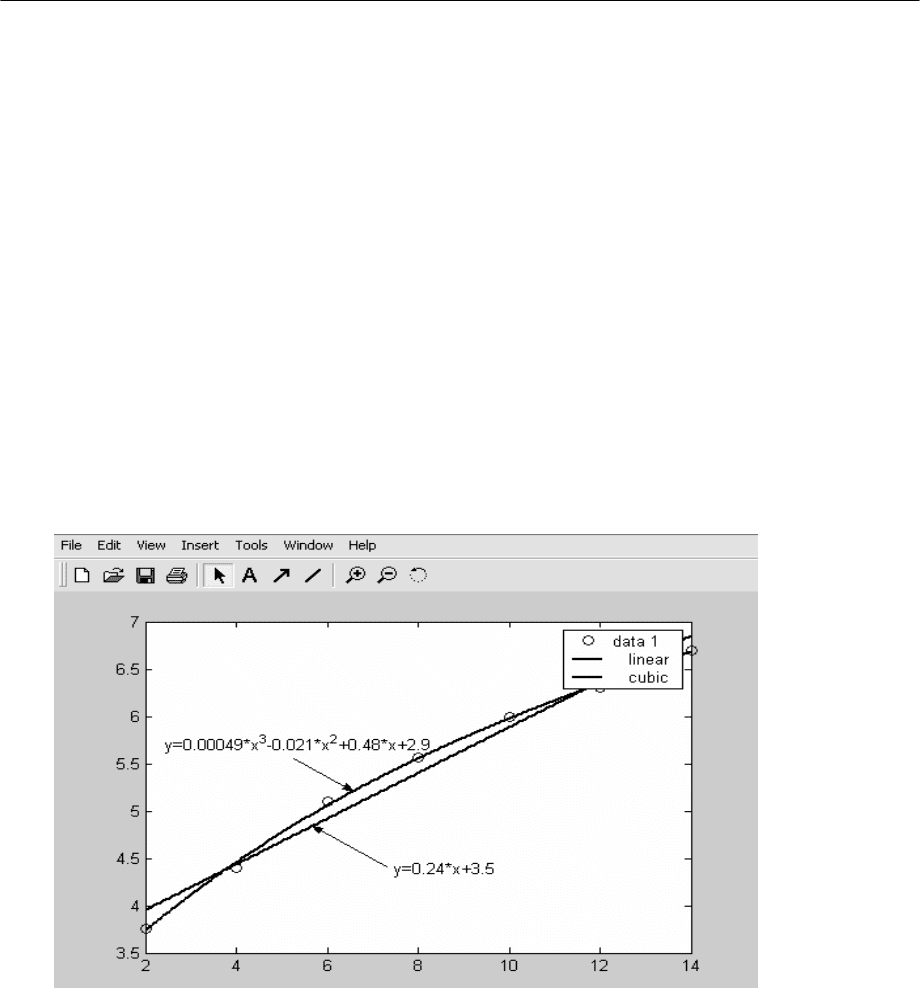
Пусть некая зависимость y(x) задана векторами координат ее точек:

>> x=[2,4,6,8,10,12,14];

>> y=[3.76,4.4,5.1,5.56,6,6.3,6.7];

>> plot(x,y,'o');

Ниже показан пример выполнения полиномиальной аппроксимации

для степеней полинома 1 и 3.

Опция Show equation выводит на график уравнения регрессии.

2.3.4. Интерполяция периодических функций рядом Фурье

Под интерполяцией обычно подразумевают вычисление значений

функции f(x) в промежутках между узловыми точками.

Линейная, квадратичная и полиномиальная интерполяция реализуются

при полиномиальной аппроксимации. А вот для периодических (и особенно

для гладких периодических) функций хорошие результаты может дать их

Глава 2. MATLAB

интерполяция тригонометрическим рядом Фурье. Для этого используется

следующая функция:

• interpft(x,n) — возвращает вектор у, содержащий значения

периодической функции, определенные в n равномерно расположенных

точках. Если length(x)=rr и х имеет интервал дискретизации dx, то интервал

дискретизации для у составляет dy=dx*m/n, причем n не может быть

меньше, чем r. Если X — матрица, interpft оперирует столбцами X,

возвращая матрицу Y с таким же числом столбцов, как и у X, но с n

строками. Функция y=interpft(x,n,dim) работает либо со строками, либо со

столбцами в зависимости от значения параметра dim.

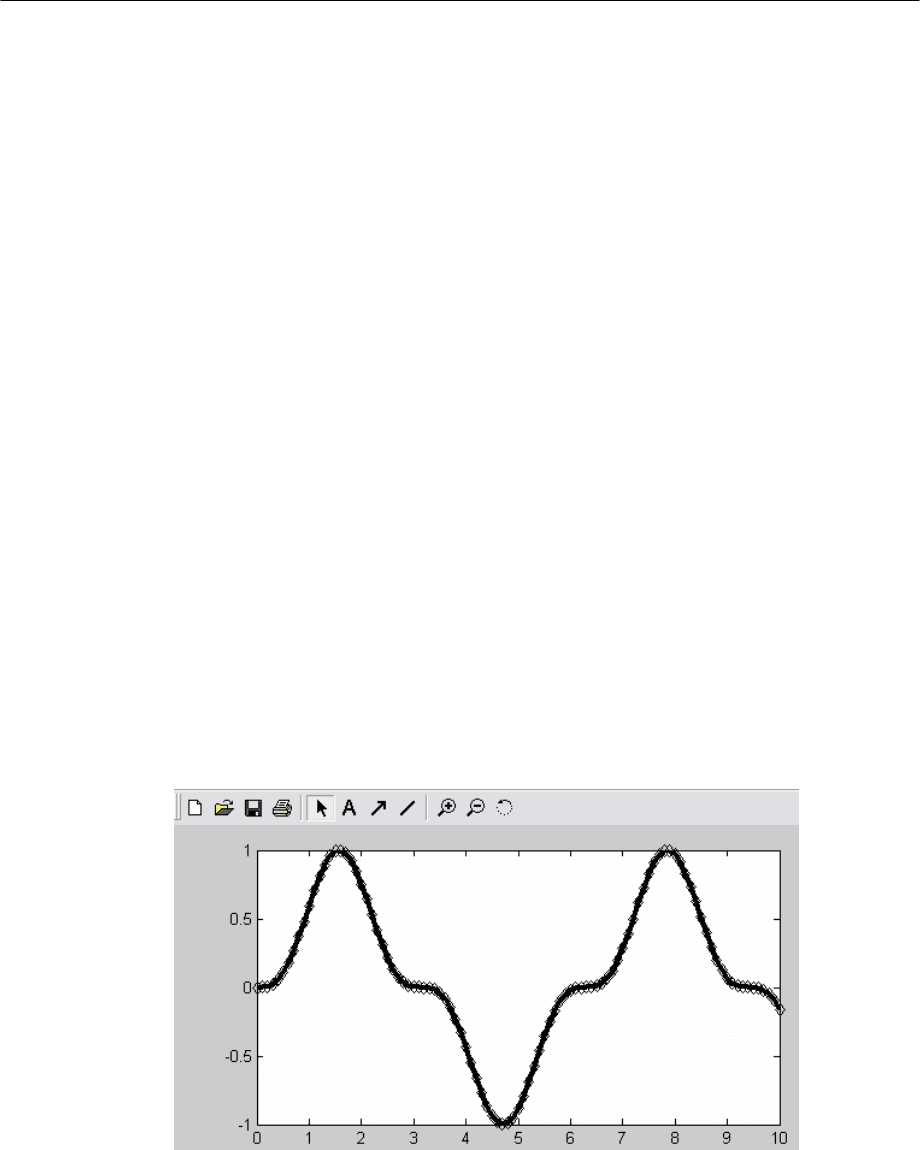
Пример:

x=0:0.1:10; y=sin(x).^3; (задаем интервал от 0 до 10 и функцию)

x1=0:0.1:10; y1=interpft(y,101); (задаем интерполирующую функцию)

plot(x,y, 'k'), (выводим график функции, черный цвет)

hold on, plot(x1,y1, 'kd') (в этом же окне (hold on) выводим

интерполирующую функцию, черный цвет, ромбики )

Рисунок иллюстрирует эффективность данного вида интерполяции на

примере функции sin(x).^3.