Higgins R.A. Engineering Metallurgy: Applied Physical Metallurgy

Подождите немного. Документ загружается.

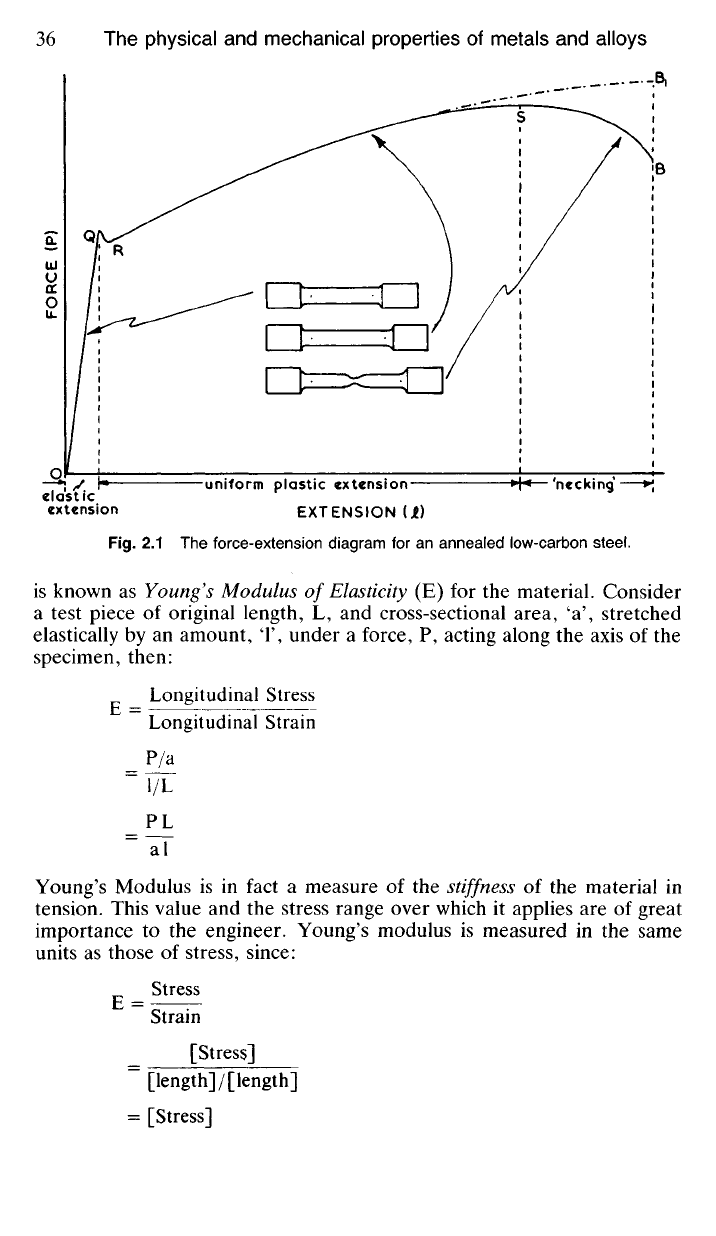
Fig.

2.1 The force-extension diagram for an annealed low-carbon steel.

is known as Young's Modulus of

Elasticity

(E) for the material. Consider

a test piece of original length, L, and cross-sectional area, 'a', stretched

elastically by an amount, T, under a force, P, acting along the axis of the

specimen, then:

Longitudinal Stress

Longitudinal Strain

P/a

l/L

_PL

~~aT

Young's Modulus is in fact a measure of the stiffness of the material in

tension. This value and the stress range over which it applies are of great

importance to the engineer. Young's modulus is measured in the same

units as those of stress, since:

_ Stress

E = —

Strain

[Stress]

~ [length]/[length]

= [Stress]

FORCE (P)

elastic

extension

uniform plastic extension

EXTENSION [Jt)

'necking

If at any point on the part of the curve under consideration the force is

relaxed then the test piece will return to its original length, extension so

far being entirely elastic.

2.31 If the test piece is stressed beyond the point O the curve deviates

from its straight-line characteristics. Q is therefore known as the elastic

limit or limit of proportionality and if the force is increased beyond this

point a stage is reached where a sudden extension takes place for no

increase in the applied force (assuming that we are testing a specimen of

annealed low-carbon steel as indicated in Fig. 2.1). An explanation of this

phenomenon, known as the yield point, R, will be given later (8.61). If

the force is now removed the elastic extension will disappear but a small

permanent plastic extension or permanent set will remain.

As the force is increased beyond the point R the test piece stretches

rapidly—first uniformly along its entire length and then locally to form a

'neck'. This 'necking' occurs just after the maximum force value has been

reached at S, and since the cross-section decreases rapidly at the neck, the

force at B required to break the test piece is less than the maximum force

applied at S.

This might be an appropriate moment at which to mention the difference

between a 'force/extension' diagram and a 'stress/strain' diagram since

these terms are often loosely used by both metallurgists and engineers.

Fig. 2.1 clearly represents a force/extension diagram since total force is

plotted against total extension, and, as the force decreases past the point

S, for reasons just mentioned, the decrease is indicated on the diagram.

Stress however is measured as force per unit area of cross-section of the

test-piece and if we wished to plot this we would need to measure the

minimum diameter of the test piece at each increment of applied force.

This would be particularly important for values of force after the point S,

since from S onwards the effective cross-section is decreasing rapidly due

to the formation of the neck. The test piece is only as strong as the force

its minimum diameter will support.

If stress were calculated on this decreasing cross-section the resulting

stress/strain diagram would follow a path indicated by the broken line to

Bi from S onwards. In practice, however, a nominal value of the tensile

strength of a material is calculated using the maximum force (at S) and the

original cross-sectional area of the test piece. Therefore:

Maximum force used

Tensile strength = _ . .—

—

Original area or cross-section

In this connection the term 'engineering stress' is often used; it implies the

force at any stage of the loading cycle divided by the original area of

cross-section of the material.

Although tensile strength is a useful guide to the mechanical properties

of a material it is not of paramount importance in engineering design.

After all, the engineer is not particularly interested in a material once it

begins to stretch plastically—unless of course he is a production engineer

engaged in deep-drawing or some other metal-forming process. In the case

of structural or constructional engineering, the elastic limit, Q, will be of

far greater significance than tensile strength.

2.32 The form of force/extension diagram described above is in fact a

special case, obtained only for wrought irons and low-carbon steels in the

soft condition (8.61). Most alloys, particularly if they have been heat-

treated or cold-worked, show neither a definite elastic limit nor a yield

point and give, on test, diagrams of the types shown in Figs. 2.2 and 2.3.

FORCE

EXTENSION

Fig.

2.2 The effects of heat-treatment on the force-extension diagram of carbon steel. (A)

is in the quenched condition; (B) is quenched and tempered; and (C) represents the annealed

condition.

EXTENSION

Fig.

2.3 Typical force-extension diagrams for a non-ferrous alloy, showing the absence of

a well-defined yield point. (D) represents the cold-worked condition, and (E) the fully annealed

condition.

Since the yield point is of greater importance to the engineer than the

tensile strength

itself,

it becomes necessary to specify a stress which corre-

sponds to a definite amount of permanent extension as a substitute for the

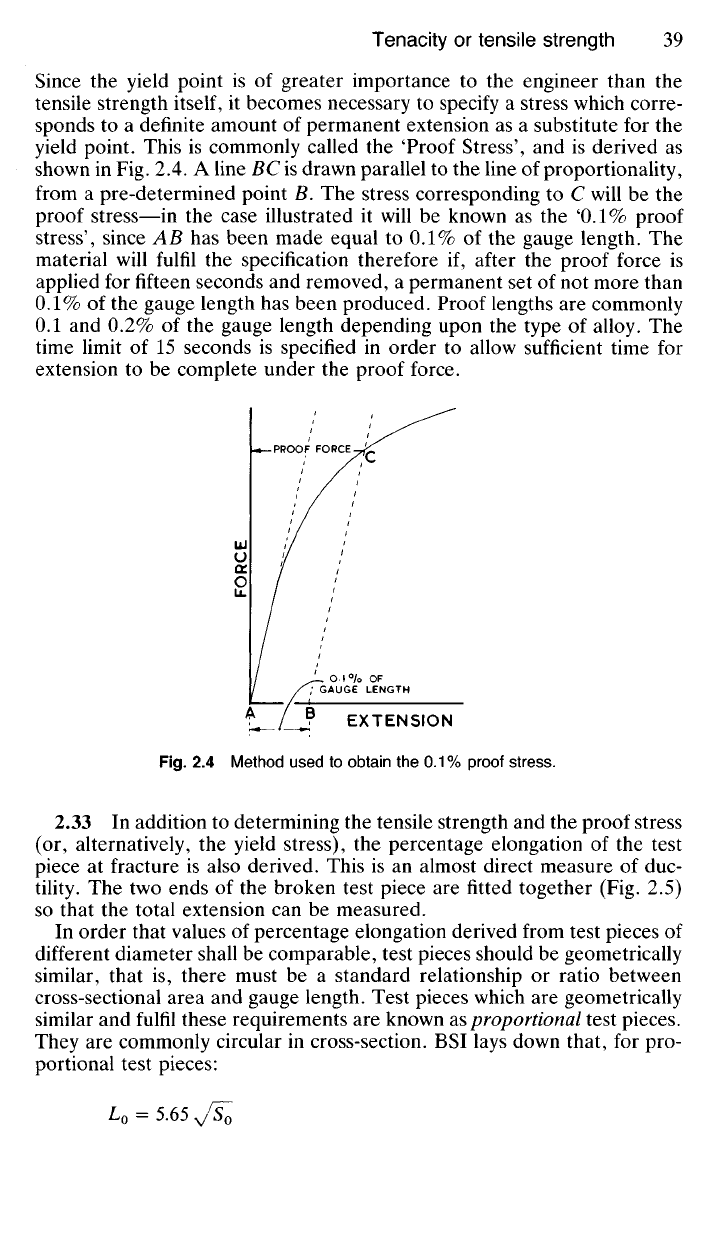
yield point. This is commonly called the 'Proof Stress', and is derived as

shown in Fig. 2.4. A line BC is drawn parallel to the line of proportionality,

from a pre-determined point B. The stress corresponding to C will be the

proof stress—in the case illustrated it will be known as the '0.1% proof

stress',

since AB has been made equal to 0.1% of the gauge length. The

material will fulfil the specification therefore if, after the proof force is

applied for fifteen seconds and removed, a permanent set of not more than

0.1%

of the gauge length has been produced. Proof lengths are commonly

0.1 and 0.2% of the gauge length depending upon the type of alloy. The

time limit of 15 seconds is specified in order to allow sufficient time for

extension to be complete under the proof force.

Fig.

2.4 Method used to obtain the 0.1 % proof stress.

2.33 In addition to determining the tensile strength and the proof stress

(or, alternatively, the yield stress), the percentage elongation of the test

piece at fracture is also derived. This is an almost direct measure of duc-

tility. The two ends of the broken test piece are fitted together (Fig. 2.5)

so that the total extension can be measured.

In order that values of percentage elongation derived from test pieces of

different diameter shall be comparable, test pieces should be geometrically

similar, that is, there must be a standard relationship or ratio between

cross-sectional area and gauge length. Test pieces which are geometrically

similar and fulfil these requirements are known as proportional test pieces.

They are commonly circular in cross-section. BSI lays down that, for pro-

portional test pieces:

FORCE

PROOF FORCE

O l°/o OF

GAUGE LENGTH

Fig.

2.5 The

determination

percentage elongation

and

percentage reduction

area.

where L

is the gauge length and So the original area of cross-section. This

formula has been accepted by international agreement and SI units are

used. For test pieces of circular cross-section it gives a value

^ 5d

where 'd' is the diameter at the gauge length. Thus a test piece 200 mm

in cross sectional area will have a diameter of 15.96 mm (16 mm) and

hence a gauge length of 80 mm. Some old tensile testing machines may

still be calibrated in 'tons force'. Since 10 kN =

1.00361

tonf,

dual value

scales are not necessary, since, within the accuracy required, 1 tonf = 10

kN.

2.34 The smallest diameter, S

, of the neck is measured and from it

the percentage reduction in area calculated (Fig. 2.5). Thus, from our

complete set of observations we can derive the following values:

,,,.,.,.

Yield force

(a) Yield stress = . .

—

Original area of cross-section

Proof force \

or Proof stress =

Original area of cross-section J

Maximum force

(b) Tensile strength = ——— -

:—

Original area of cross-section

Increase in gauge length x 100

—

——

Original gauge length

(d) Percentage reduction in area =

(Original area of cross-section

—

Final area of cross section) x 100

Original area of cross-section

In terms of SI units stress is measured in N/m

. However, since it is

difficult to appreciate the very large force necessary to break a test piece

(original area

cross section)

'neck'

gauge

length,

°/o

Elongation

°/o

Reduction

in area

Plate 2.1 The Avery-Denison Servo-controlled Tensile Testing Machine, with an applied

force capacity of 60OkN.

The straining unit which is shown on the left embodies a double-acting hydraulic cylinder

and ram. The force on the test piece is measured by load-sensitive cells and is indicated on

the display panel of the control console shown on the right. The full load/extension cycle is

electronically controlled and a permanent trace is produced. (Courtesy of Messrs Avery-

Denison Ltd, Leeds).

of one square metre in cross-section, most bodies, including BSI, quote

tensile stress in metals in N/mm

. This at least enables the student to relate

the tensile strength of a steel to the force necessary to break in tension

one of the thicker steel strings on his guitar.

2.35 Early tensile-testing machines were of the simple beam type in

which the applied force was magnified by using a first-order lever system.

With such machines an accurate evaluation of extension was possible up to

the elastic limit by using a sensitive extensometer but beyond the maximum

force, determinations of force/extension characteristics were impossible

because the test piece fractured quickly as soon as necking began, there

being no means of relaxing the applied force rapidly enough. Modern

machines however are usually servo-hydraulically loaded (Plate 2.1) so that

a complete force/extension relationship can be obtained. Since advanced

computer control technology is now employed automatic calculation of

proof stress, yield stress, ultimate tensile stress and percentage elongation

are carried out; whilst software is available for cycling and data storage.

Software programs can be written to meet other specific requirements.

These machines can also be used for compression and transverse testing,

and vary in size between large machines with a capacity of 1300 kN and

small bench models having a capacity of only 20 kN.

2.36. In situations where a large amount of energy is being expended

against gravity as in various types of aero-space travel—or even driving

the humble 'tin Lizzie' up a hill—it becomes necessary to relate the tensile

properties of a material to its relative density. Thus, what used to be called

the 'strength-to-weight ratio' became important in the design of both land

and air transport vehicles. In modern terminology this became 'specific

strength'. Thus:

.„ , Tensile strength of material

Specific strength = —

Relative density of material

When stiffness is the prime consideration, however, Young's Modulus of

Elasticity is a more appropriate guide to the required properties and a

value termed specific modulus is now generally accepted as being relevant,

ie—

Young's modulus of elasticity

Specific modulus of elasticity =

iTTT-—"A

Relative density

Hardness Tests

2.40 Classically, hardness could be defined as the resistance of a surface

to abrasion, and early attempts to measure surface hardness were based

on this concept. Thus in the Turner Sclerometer a loaded diamond point

was drawn across the surface of the test piece and the load increased until

a visible scratch was produced. In Moh's Scale—still used to evaluate the

hardness of minerals—substances were arranged in order of hardness such

that any material in the scale would scratch any material listed below it.

Thus diamond (with a hardness index of 10) heads the list whilst talc (with

an index of 1) is at the foot of the scale.

Whilst such methods undoubtedly reflect a true concept of the funda-

mental meaning of hardness, they have been abandoned in favour of

methods which are capable of greater accuracy but in which the resistance

of the surface layers to plastic deformation under static pressure is

measured rather than true hardness. In most of these methods the static

force used is divided by the numerical value of the surface area of the

resulting impression to give the hardness index.

2.41 The Brinell Test, probably the best known of the hardness tests,

was devised by a Swede, Dr. Johan August Brinell in 1900. In this test a

hardened steel ball is pressed into the surface of the test piece using the

appropriate specified force. The diameter of the impression so produced

is then measured and the Brinell Hardness Number, H

derived from:

Force, P

Surface area of impression

It can be shown that the surface area of the impression is

n—l D - yJD

- d

j where D is the diameter of the ball and 'd' the diameter

of the impression (Fig. 2.6). Since we are dealing with the actual area of

the curved surface of the impression the derivation of the above expression

is quite involved.

Hence,

and the units will be kgf/mm

. To obviate tedious calculations H

is found

by reference to the appropriate set of tables.

2.42 It is obviously important that the stress produced by the indenter

at the surface of the test piece shall suit the material being tested. If for

example in testing a soft metal we use a force which is too great relative

to the diameter of the ball, we shall get an impression similar to that

Fig.

2.6 The relationships between ball diameter, depth of impression and dimensions of

the test piece in the Brinell-type test.

not less

than 8h

TEST PIECE

not less

than 3D

indicated in Fig. 2.7A. Here the ball has sunk to its full diameter and the

result is obviously meaningless. The impression shown in Fig. 2.7B on

the other hand would be obtained if the force were too small relative to

the ball diameter and here the result would be likely to be very uncertain.

For different materials then, the ratio P/D

has been standardised in order

to obtain accurate and comparable results. P is measured in kgf and D in

mm.

Material Approximate H

range PID

ratio used

Steel and cast iron Over 100 30

Copper, copper alloys and .~

aluminium alloys 30-200

Aluminium 15-100 5

Tin, lead and their alloys 3-20 1

INCORRECT CORRECT

Fig.

2.7 The influence of depth of impression on the accuracy of a Brinell determination.

Thus in testing a piece of steel we can use either a 10-mm ball in conjunc-

tion with a 3000 kgf load; a 5 mm ball with a 750 kgf load; or a 1 mm ball

with a 30 kgf load. In the interests of accuracy it is always advisable to use

the largest ball diameter that is possible. The limiting factors will be the

width and thickness of the test piece, and the small ball would be used for

thin specimens, since by using the large ball we would probably be, in

effect, measuring the hardness of the table supporting our test piece. The

thickness of the specimen should be at least eight times the depth, 'h', of

the impression (Fig. 2.6). Similarly the width of the test piece must be

adequate to support the applied force and it is recommended that the

distance of the centre of the indentation from the edge of the test piece

shall be at least three times the diameter of the indenting ball.

2.43 The Vickers Hardness Test—or Diamond Pyramid Hardness

Test —uses as its indenter a diamond square-based pyramid (Fig. 2.8)

which will give geometrically similar impressions under different applied

forces.

This eliminates the necessity of deciding the correct P/D

ratio as is

required in the Brinell test. Moreover, the diamond is more reliable for

hard materials which have a hardness index of more than 500, since it does

not deform under pressure to the same extent as a steel ball. Using the

diamond point, however, does not eliminate the necessity of ensuring that

B C

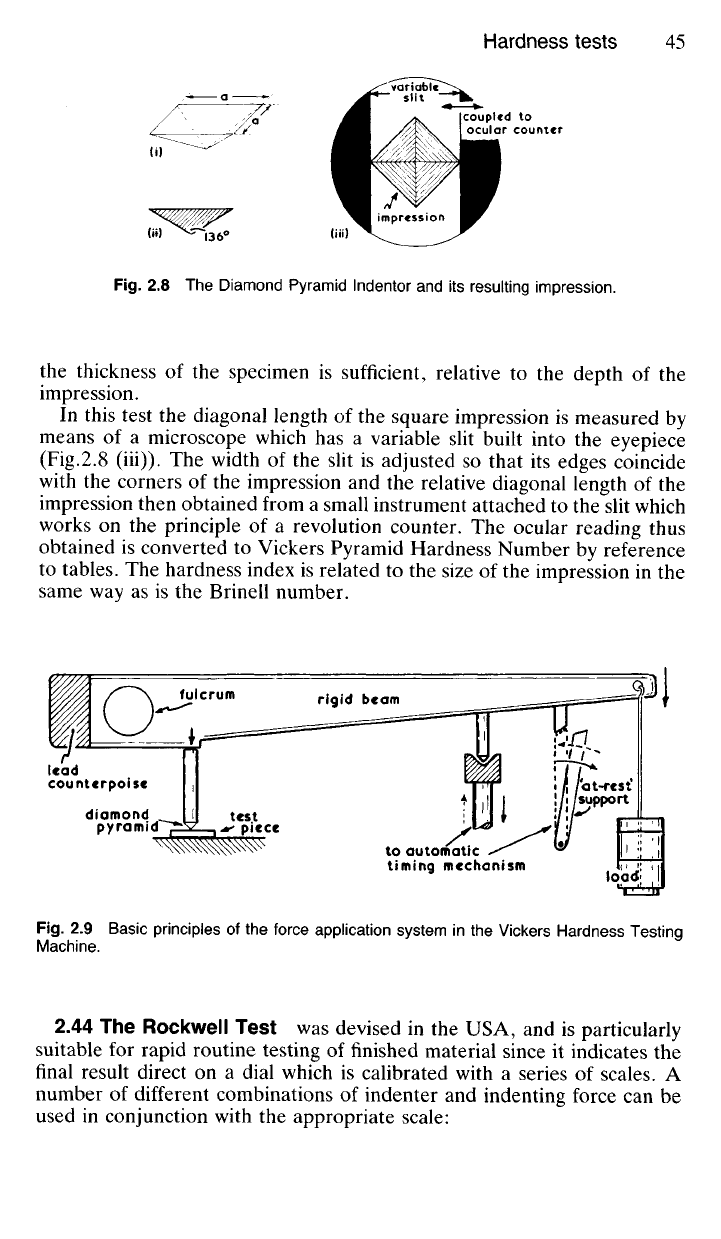
Fig.

2.8 The Diamond Pyramid lndentor and its resulting impression.

the thickness of the specimen is sufficient, relative to the depth of the

impression.

In this test the diagonal length of the square impression is measured by

means of a microscope which has a variable slit built into the eyepiece

(Fig.2.8 (iii)). The width of the slit is adjusted so that its edges coincide

with the corners of the impression and the relative diagonal length of the

impression then obtained from a small instrument attached to the slit which

works on the principle of a revolution counter. The ocular reading thus

obtained is converted to Vickers Pyramid Hardness Number by reference

to tables. The hardness index is related to the size of the impression in the

same way as is the Brinell number.

Fig.

2.9 Basic principles of the force application system in the Vickers Hardness Testing

Machine.

2.44 The Rockwell Test was devised in the USA, and is particularly

suitable for rapid routine testing of finished material since it indicates the

final result direct on a dial which is calibrated with a series of scales. A

number of different combinations of indenter and indenting force can be

used in conjunction with the appropriate scale:

fulcrum

rigid beam

lead

counterpoise

diamond .

pyramid

test

piece

to automatic

timing mechanism

at-rest'

support

load

variable

slit

coupled

ocular counter

impression

(iii)

(i)

(i»)