Хермен Г. Восстановление изображений по проекциям: Основы реконструктивной томографии

Подождите немного. Документ загружается.

298

ГЛАВА

Таблица

15.1

г Р L

(«}

1,6,2)

(2,5,8)

1.6,2,8)

(5.8,7,10)

1,6,2,8,7,10)

(8.7,10,4)

1,6,2,8,7,10,4)

8 (7,10,4) [1,6,2,8.7,10,4)

(10,4,9) Ц6,2,8.7,10,4,9)

10 (4,91 [1,6,2,8,7,10,4,9)

(9,

13)

1,6,2,8,7,10,4,9,13!

9 (13,12)

1,6.2,8.7.10.4.9,13,12)

(12,3,14) [1,6,2,8,7,10,4,9,13,12,3,14)

(3,14)

1,6,2,8,7,10,4,9,13,12,3,14)

(14,11)

1,6,2,8,7,10,4,9,13,12,3,14,11)

(И)

1,6,2,8,7,10.4,9,13,12,3,14,11)

1,6,2,8,7,10,4,9,13,12,3,14,11)

ема в направлении на центр к-го элементарного объема, может иметь одно

из шести возможных значений). Можно использовать это свойство для

уменьшения затрат времени по проверке наличия граней в «перечне» L в 6

раз.

Кроме того, разбиение L на шесть групп в соответствии с выбранным

критерием окажется также полезным при отображении поверхностей орга-

нов,

как это будет видно в следующем разделе.

15 3. УСТРАНЕНИЕ СКРЫТЫХ ЧАСТЕЙ ПОВЕРХНОСТИ

Как было показано в предыдущем разделе, алгоритм определения гра-

ниц органов дает «перечень» L граней, каждая из которых представляет со-

бой упорядоченную пару элементарных объемов, однако теперь целесо-

образно рассматривать грань в виде элементов квадратной формы, занима-

ющих одно из шести возможных положений (три взаимно перпендикуляр-

ные пары противоположных направлений).

Для простоты последующего анализа будем предполагать, что внешняя

область содержит в себе внутреннюю область, что обычно всегда можно

сделать для любой интересующей нас поверхности путем соответствующе-

го выбора диапазона чисел Хаунсфилда, который определяет множество Q.

Предположим, что имеется экран системы отображения, расположенный в

пространстве в фиксированном положении, причем плоскость экрана пол-

лностью содержится во внешней по отношению к поверхности области.

ТРЕХМЕРНОЕ ОТОБРАЖЕНИЕ ОТДЕЛЬНЫХ ОРГАНОВ

299

f Л

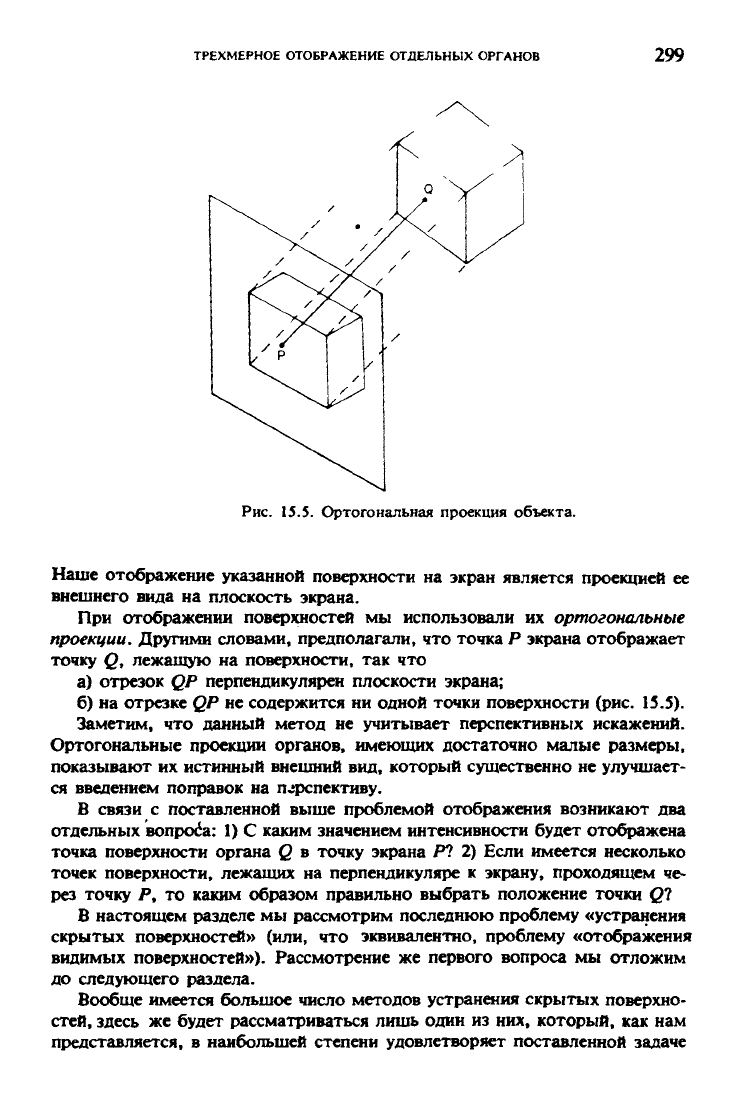
Рис. 15.5. Ортогональная проекция объекта.

Наше отображение указанной поверхности на экран является проекцией ее

внешнего вида на плоскость экрана.

При отображении поверхностей мы использовали их ортогональные

проекции. Другими словами, предполагали, что точка Р экрана отображает

точку Q

лежащую на поверхности, так что

а) отрезок QP перпендикулярен плоскости экрана;

б) на отрезке QP не содержится ни одной точки поверхности (рис. 15.5).

Заметим, что данный метод не учитывает перспективных искажений.

Ортогональные проекции органов, имеющих достаточно малые размеры,

показывают их истинный внешний вид, который существенно не улучшает-

ся введением поправок на перспективу.

В связи с поставленной выше проблемой отображения возникают два

отдельных вопроса: 1) С каким значением интенсивности будет отображена

точка поверхности органа Q в точку экрана Р? 2) Если имеется несколько

точек поверхности, лежащих на перпендикуляре к экрану, проходящем че-

рез точку Р, то каким образом правильно выбрать положение точки Q1

В настоящем разделе мы рассмотрим последнюю проблему «устранения

скрытых поверхностей» (или, что эквивалентно, проблему «отображения

видимых поверхностей»). Рассмотрение же первого вопроса мы отложим

до следующего раздела.

Вообще имеется большое число методов устранения скрытых поверхно-

стей,

здесь же будет рассматриваться лишь один из них, который, как нам

представляется, в наибольшей степени удовлетворяет поставленной задаче

300

ГЛАВА 15

отображения органов и который обычно называется буферным Z-

алгоритмом.

С каждой точкой (с каждым элементом растра) Р на экране устройства

отображения мы свяжем две

величины:

яркость Ь(Р)

расстояние

d(P) от

поверхности

до

экрана.

Первоначально каждой точке на экране мы припи-

сываем нулевое значение яркости, соответствующее наиболее темным ме-

стам изображения, и достаточно большое (практически бесконечное) рас-

стояние до экрана. Если элементарная площадка а поверхности ориентиро-

вана перпендикулярно плоскости экрана, то она на нем не отображается.

Все другие элементарные площадки, составляющие данную поверхность,

отображаются независимо друг от друга в соответствии со следующей

процедурой.

Для каждой грани а определяем все точки Р на экране, которые могли

бы быть отображены на нем, если бы данная грань была единственной. За-

тем полученные точки последовательно исследуются по такой методике:

для каждой точки Р находим такую точку Q на грани а, что отрезок PQ

становится перпендикулярным экрану. Пусть d(Q) -- расстояние точки Q

от экрана (т.е. d{Q) — длина перпендикуляра PQ), a b(Q) — яркость, кото-

рую можно было бы приписать точке Р, если бы данная элементарная пло-

щадка была единственной. Если d(Q) < d(P), то мы заменяем величину

Ь(Р) на b(Q)

а величину а(Р) — на d(Q). В противном случае, когда d(Q) не

меньше d(P), то величины Ь(Р) и d(P) остаются неизменными.

Аналогичным образом мы поступаем со всеми остальными гранями,

причем видимые грани отображаются на экране, а скрытые площадки (или

скрытые их части) не дают вклада в изображение.

Имеется три способа увеличить быстродействие только что рассмотрен-

ного общего буферного Z-алгоритма применительно к проблеме отображе-

ния.

Первый их них, некорректное доказательство справедливости которого

мы опускаем, использует следующие факты: если ни одна из граней а и /3

не перпендикулярна плоскости экрана и если точки А и В находятся на эле-

ментарных площадках а и 0 соответственно (но не на их краях), так что

отрезок АВ перпендикулярен экрану, то d{A) < d(B) тогда и только тогда,

когда d[C(a)] < d[C{0)]

где С(а) и С(0) обозначают положение централь-

ных точек граней а и

/3.

Этот результат свидетельствует о том, что в рам-

ках буферного Z-алгоритма в любой точке Q грани а можно заменить ве-

личину d{Q) на d[C(a)\ и закончить отображение. Во втором способе также

можно предположить ввиду малости граней, что все точки грани отобра-

жаются с одинаковыми яркостями, и поэтому в каждой точке Q на грани а

можно заменить величину b(Q) на

Ъ\С{а)].

В третьем способе отображение половины граней вообще не требуется.

Для любой фиксированной ориентации экрана необходимо рассматривать

самое большее три из шести частичных перечней, описанных в последнем

разделе, и при этом гарантируется, что грани, принадлежащие трем

остальным подперечням, оказываются скрытыми, что следует, как указы-

ТРЕХМЕРНОЕ ОТОБРАЖЕНИЕ ОТДЕЛЬНЫХ ОРГАНОВ

301

валось, из принадлежности поверхностей к поверхностям жорданового ти-

па.

Серию подобных отображений можно получить путем перемещения

экрана.

15.4.

МЕТОД НАЛОЖЕНИЯ ТЕНЕЙ

Нам желательно отобразить видимые части регистрируемой поверхно-

сти на экране ЭЛТ так, чтобы их внешний вид имел сходство с реальной

поверхностью объекта при той же ориентации. Подобное трехмерное пред-

ставление объекта на устройстве растрового типа достигается путем нало-

жения теней на изображение (т.е. путем присвоения различным отображае-

мым точкам на экране разных значений градаций яркости). Существует ряд

вариантов отображения формы и высоты поверхности, однако мы рас-

смотрим только два из них — отображение с учетом расстояния Z и ориен-

тации поверхности.

Исходным предположением в этом достаточно простом случае является

то,

что свет распространяется от плоского источника параллельным пуч-

ком перпендикулярно плоскости экрана. Интенсивность, присваиваемая

точке Р экрана и отображающей точку Q элементарной площадки в трех-

мерном пространстве, зависит от расстояния между точкой Q и источни-

ком света, а также от угла между нормалью к поверхности и направлением

на источник света.

С точки зрения вычислений весьма удобно то, что элементарные объе-

мы имеют форму кубов. Поскольку каждый элемент поверхности имеет

форму квадрата, ориентированного в одном их трех направлений, то необ-

ходимо учитывать лишь три положения нормали. Кроме того, ввиду мало-

сти элементов поверхности можно предположить без внесения существен-

ных погрешностей в окончательные результаты, что все точки элемента

поверхности а имеют одно и то же значение d[C(a)] расстояния по Z, а

именно равное расстоянию до его центра, величина которого уже вычисле-

на в процессе определения скрытых частей поверхности.

На практике из-за ограниченного числа ориентации граней зарегистри-

рованной поверхности требуются еще кое-какие операции, поскольку ото-

бражаемые поверхности часто выглядят неровными, шероховатыми, тогда

как в действительности они, вероятно, достаточно гладкие.

Перечислим здесь три метода, предложенные для преодоления указан-

ных недостатков и используемые либо отдельно, либо в сочетании друг с

другом:

а) пропускание полученного изображения через фильтр нижних частот

для сглаживания его внешней поверхности, что эквивалентно его свертке с

функцией, не имеющей в спектре высокочастотных, компонент;

б) использование предположения о том, что экран устройства отобра-

жения имеет большее разрешение, чем это есть в действительности, и ото-

302

ГЛАВА IS

бражение на реальный экран данных, усредненных по такому виртуальному

экрану;

в) существенно ослабить влияние зависимости от угла между световым

пучком и нормали к поверхности по сравнению с расстоянием вдоль оси Z.

Необходимо отметить, что ни один из вышеуказанных методов не

удовлетворяет нас полностью. Например, третий метод, по существу, уст-

раняет важную информацию о глубине, содержащуюся в величине угла

между направлением распространения света и нормалью к поверхности.

Два других метода не позволяют устранить трудность, которую мы рас-

смотрим ниже.

Представим себе часть плоской поверхности исходного объекта, кото-

рал перпендикулярна направлению распространения света. Если ориентация

двух граней элементарных ячеек также перпендикулярна световому пучку,

то отмеченная выше плоская поверхность аппроксимируется гранями эле-

ментарных объемов, параллельных друг другу и перпендикулярных пучку.

В этом случае в каждой точке нормаль к зарегистрированной поверхности

совпадает с направлением распространения света, и поверхность окажется

равномерно яркой. Если ориентация элементарных объемов оказывается

выбранной под углом т/4 к плоской части поверхности исходного объекта,

то плоская поверхность может быть аппроксимирована гранями элемен-

тарных объемов, которые составляют угол т/4 с плоской площадкой по-

верхности (и, следовательно, с направлением светового пучка). В данном

случае в каждой точке нормаль к зарегистрированной поверхности состав-

ляет угол т/4 с направлением распространения света, и поверхность будет

выглядеть равномерно освещенной, однако не такой яркой, как в предыду-

щем случае.

Последнее является серьезным недостатком принятой нами модели, ко-

торый можно преодолеть либо методом наложения теней с использовани-

ем данных об ориентации рассматриваемой элементарной грани и граней,

ее окружающих, либо с использованием элементарных площадок с более

сложной, чем квадратной, формой. Однако, как это будет показано в сле-

дующем разделе, высокого качества трехмерного отображения можно до-

стичь в действительности при использовании в виде основных дистанцион-

ных признаков расстояния вдоль оси Z с последующим применением к по-

лученному изображению операции низкочастотной фильтрации.

15.5.

ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ

Наш первый пример относится к случаю отображения системы желу-

дочков головного мозга человека, которое было сделано по восьми смеж-

ным срезам толщиной 8 мм. На рис. 15.1 (вверху) приведены фрагменты из

80 х 80 элементов изображения трех из указанных срезов. Система желу-

дочков изображена на фрагментах полностью. Размер элемента изображе-

ния в срезах составлял 1,5 х 1,5 мм, что соответствовало размеру элемен-

ТРЕХМЕРНОЕ ОТОБРАЖЕНИЕ ОТДЕЛЬНЫХ ОРГАНОВ

303

тарного объема 1,5 х 1,5 х 8 мм, хотя более желательна, как и в пре-

дыдущих разделах, была бы кубическая форма элементарных объемов.

Чтобы преобразовать элементарные объемы в кубические, использовалась

линейная интерполяция данных для оценки 38 смежных срезов толщиной

1,5 мм. Таким образом, формируется массив из 80 х 80 х 32 чисел, харак-

теризующих среднюю плотность множества элементарных объемов куби-

ческой формы.

Причина, по которой желудочки мозга выглядят более темными, чем

окружающие ткани, состоит в том, что они содержат спинномозговую

жидкость с несколько меньшим, чем у мозга, линейным коэффициентом ос-

лабления (табл. 4.1). Поэтому диапазон & значений, введенный в

разд.

15.1, оказался таким, что его верхний предел стал больше, чем линей-

ный коэффициент ослабления цереброспинальной жидкости, но меньшим,

чем для самого мозга. Последнее означает, что все элементарные объемы,

характеризующие спинномозговую жидкость, имеют числа Хаунсфилда в

указанном диапазоне ^ Таким образом, множество Q элементарных объе-

мов,

в которых числа Хаунсфилда лежат в диапазоне <^(разд. 15.2), соде-

ржит не только области желудочков, но также и другие части мозга, либо

заполненные спинномозговой жидкостью, либо не заполненные ей, но име-

ющие по разным причинам такие же числа Хаунсфилда в данном диапазо-

не,

например, вследствие наличия шума в исходных данных, артефактов

при реконструкции и т.д. Элементарные объемы, которые принадлежат

множеству Q, изображены в виде светлых областей в нижней части

рис. 15.1. Анатомическая картина соответствующих частей системы желу-

дочков, показывающая в том числе положение corpora quadragemina («чет-

верохолмие»), приведена на рис. 15.6.

Рис. 15.6. Анатомическая структура фрагмента системы желудочков головного моз-

га человека.

/ — передние рога латерального желудочка; 2 — третий желудочек; S — четверохолмие;

4 — задние рога латерального желудочка.

304

ГЛАВА 15

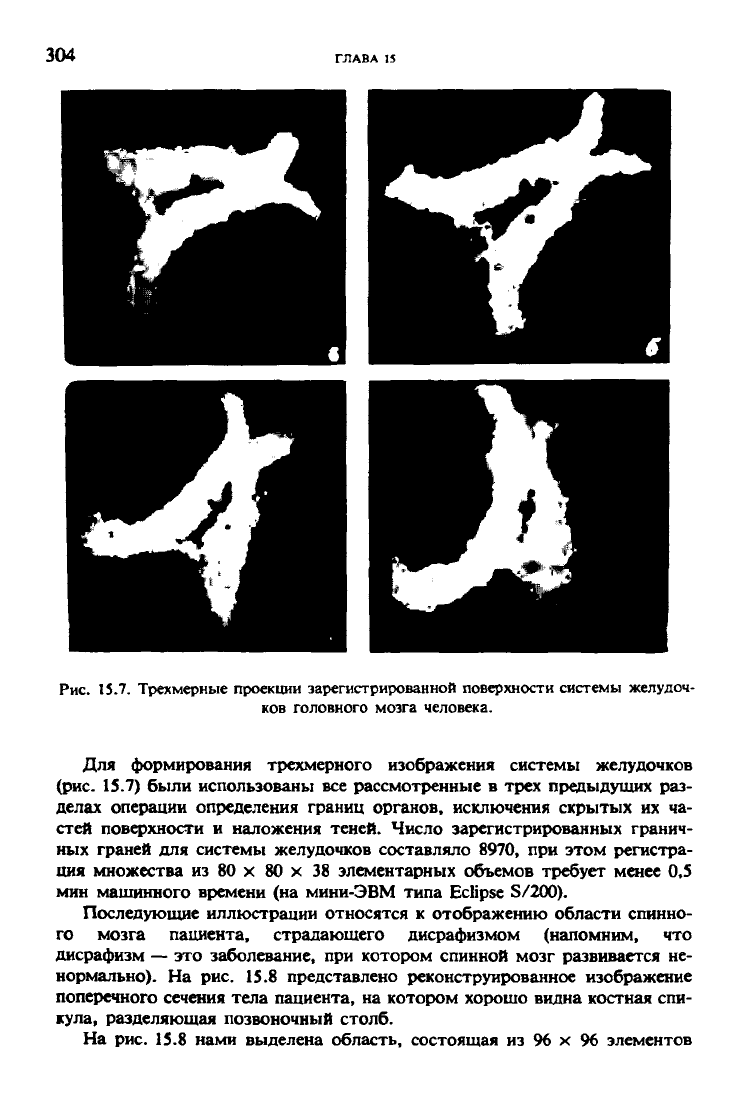
Рис. 15.7. Трехмерные проекции зарегистрированной поверхности системы желудоч-

ков головного мозга человека.

Для формирования трехмерного изображения системы желудочков

(рис. 15.7) были использованы все рассмотренные в трех предыдущих раз-

делах операции определения границ органов, исключения скрытых их ча-

стей поверхности и наложения теней. Число зарегистрированных гранич-

ных граней для системы желудочков составляло 8970, при этом регистра-

ция множества из 80 х 80 х 38 элементарных объемов требует менее 0,5

мин машинного времени (на мини-ЭВМ типа Eclipse S/200).

Последующие иллюстрации относятся к отображению области спинно-

го мозга пациента, страдающего дисрафизмом (напомним, что

дисрафизм — это заболевание, при котором спинной мозг развивается не-

нормально). На рис. 15.8 представлено реконструированное изображение

поперечного сечения тела пациента, на котором хорошо видна костная спи-

кула, разделяющая позвоночный столб.

На рис. 15.8 нами выделена область, состоящая из 96 х % элементов

ТРЕХМЕРНОЕ ОТОБРАЖЕНИЕ ОТДЕЛЬНЫХ ОРГАНОВ

305

Рис. 15.8. Поперечное сечение тела пациента, страдающего диерафизмом.

Костная спикула показана стрелкой. Рамкой обведена область, состоящая

из 96 х 96

элементар-

ных объемов

содержащая изображение спинного мозга.

изображения и содержащая изображение ствола спинного мозга. Каждая

из ячеек имеет размеры 0,8 х 0,8 мм. Из серии восьми смежных срезов

толщиной 1,5 мм методом линейной интерполяции формировался трехмер-

ный массив усредненных плотностей, состоящий из % ж 96 х 14 элемен-

тарных объемов размером 0,8 х 0,8 х 0,8 мм. Был точно установлен та-

кой диапазон чисел Хаунсфилда, чтобы элементарные объемы от кости и

окружающих тканей можно было различить, и в результате получены изо-

бражения двух последовательных слоев (рис. 15.9), содержащих

96 х % х 14 элементарных объемов.

Проблема отображения срезов толщиной 1,5 мм состоит в том, что для

«заполнения» элементарными объемами значительной части спинного моз-

га требуется большое число срезов. Один и тот же пациент должен быть

просканирован 10 раз для получения смежных срезов толщиной 5 мм, а за-

тем по этим срезам необходимо формировать трехмерный массив, соде-

ржащий в данном случае 96 х % х 57 элементарных объемов размером

0,8 х 0,8 х 0,8 мм. Вид слоев, изображенный на рис. 15.10, приблизитель-

но соответствует изображению рис. 15.9, хотя между ними имеется одно

существенное отличие: числа Хаунсфилда, связанные с костной спикулой, на

рис. 15.10 оказываются ниже настолько, что на правом изображении

306

ГЛАВА 15

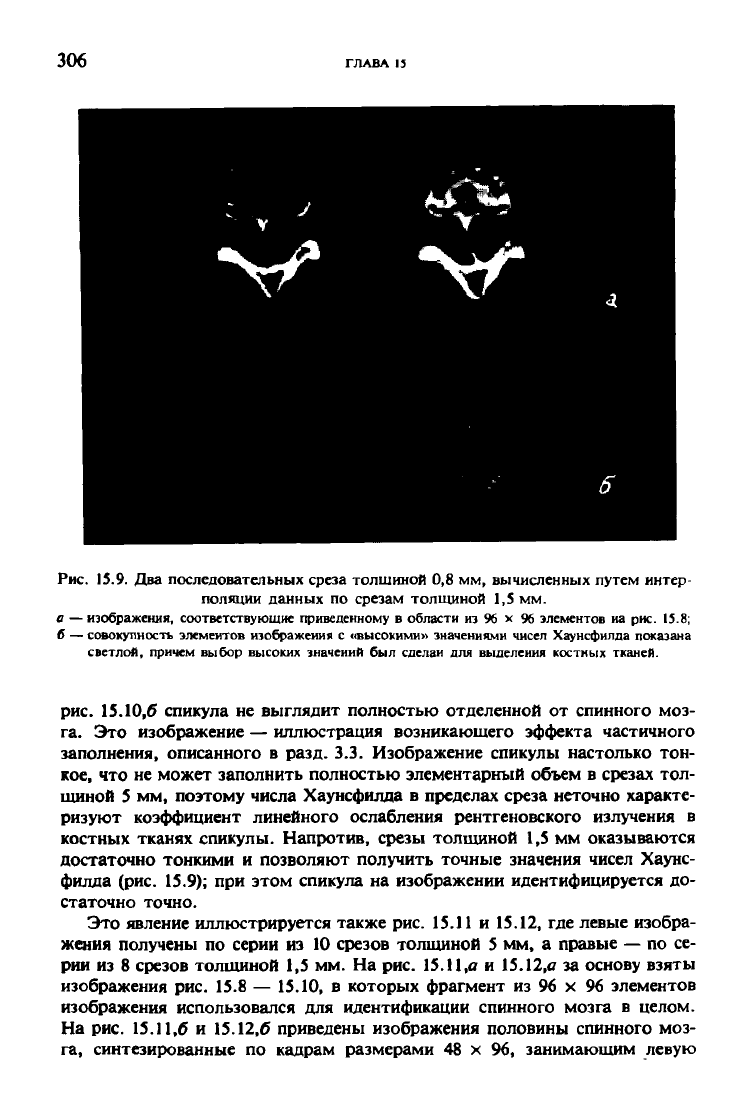
Рис. 15.9. Два последовательных среза толшиной 0,8 мм, вычисленных путем интер-

поляции данных по срезам толщиной 1,5 мм.

а — изображения, соответствующие приведенному в области из 96 х 96 элементов иа рис. 15.8;

б — совокупность элементов изображения с «высокими» значениями чисел Хаунсфилла показана

светлой, причем выбор высоких значений был сделан для выделения костных тканей.

рис. 15.10,6 спикула не выглядит полностью отделенной от спинного моз-

га.

Это изображение — иллюстрация возникающего эффекта частичного

заполнения, описанного в разд. 3.3. Изображение спикулы настолько тон-

кое,

что не может заполнить полностью элементарный объем в срезах тол-

шиной 5 мм, поэтому числа Хаунсфилла в пределах среза неточно характе-

ризуют коэффициент линейного ослабления рентгеновского излучения в

костных тканях спикулы. Напротив, срезы толшиной 1,5 мм оказываются

достаточно тонкими и позволяют получить точные значения чисел Хаунс-

филла (рис. 15.9); при этом спикула на изображении идентифицируется до-

статочно точно.

Это явление иллюстрируется также рис. 15.11 и 15.12, где левые изобра-

жения получены по серии из 10 срезов толщиной 5 мм, а правые — по се-

рии из 8 срезов толшиной 1,5 мм. На рис. 15.11,я и 15.12,а за основу взяты

изображения рис. 15.8 — 15.10, в которых фрагмент из 96 х 96 элементов

изображения использовался для идентификации спинного мозга в целом.

На рис. 15.11,6 и 15.12,6 приведены изображения половины спинного моз-

га,

синтезированные по кадрам размерами 48 х 96, занимающим левую

ТРЕХМЕРНОЕ ОТОБРАЖЕНИЕ ОТДЕЛЬНЫХ ОРГАНОВ

307

Рис. 15.10.

Два

последовательных среза толщиной

0,8

мм, полученных путем интер-

поляции данных

по

срезам толщиной

5 мм.

Данные изображения соответствуют рис. 15.9. Изображение спикулы полностью

не

воспроизво-

дится

иа

рис. 15.10,6 из-за эффекта частичного заполнения объема.

часть первоначального полного кадра размером 96 х 96. При этом можно

одновременно наблюдать как внутренние, так и внешние структуры мозга

при различной его ориентации. Это показано на рис. 15.11 и 15.12, на кото-

рых приведены две серии кинокадров, демонстрирующих изображения

спинного мозга при четырех синхронно измененных положениях пациента.

ПРИМЕЧАНИЯ

ССЫЛКИ

Выражение «хирургия

без

вмешательства» впервые использовано

[157],

чтобь

подчеркнуть потенциальные возможности методов трехмерного отображения органо

при изучении структурных

функциональных динамических характеристик сердш

легких

системы кровообращения.

Частный метод отображения произвольных сечений тела

помощью серии рекон-

струированных томограмм описан в работе

174].

В ней приведен перечень более ранних

работ как по отображению сечений, так и по вопросам определения пространственного

положения границ органов и их отображения

использованием методов, которые

ря-

де случаев существенно отличаются

от

рассмотренных

данной главе. Другой источ-

ник информации

по

рассматриваемому вопросу

— зто

обзор [4],

котором собраны

ссылки

на

работы [45,

48, 53, 60, 103, ПО, 116].