Хермен Г. Восстановление изображений по проекциям: Основы реконструктивной томографии

Подождите немного. Документ загружается.

288

В 0,24,

32 48 64 80 96 112 (26

Координата

32 48 64 80

Координата

16 32 48 64 80

Координата

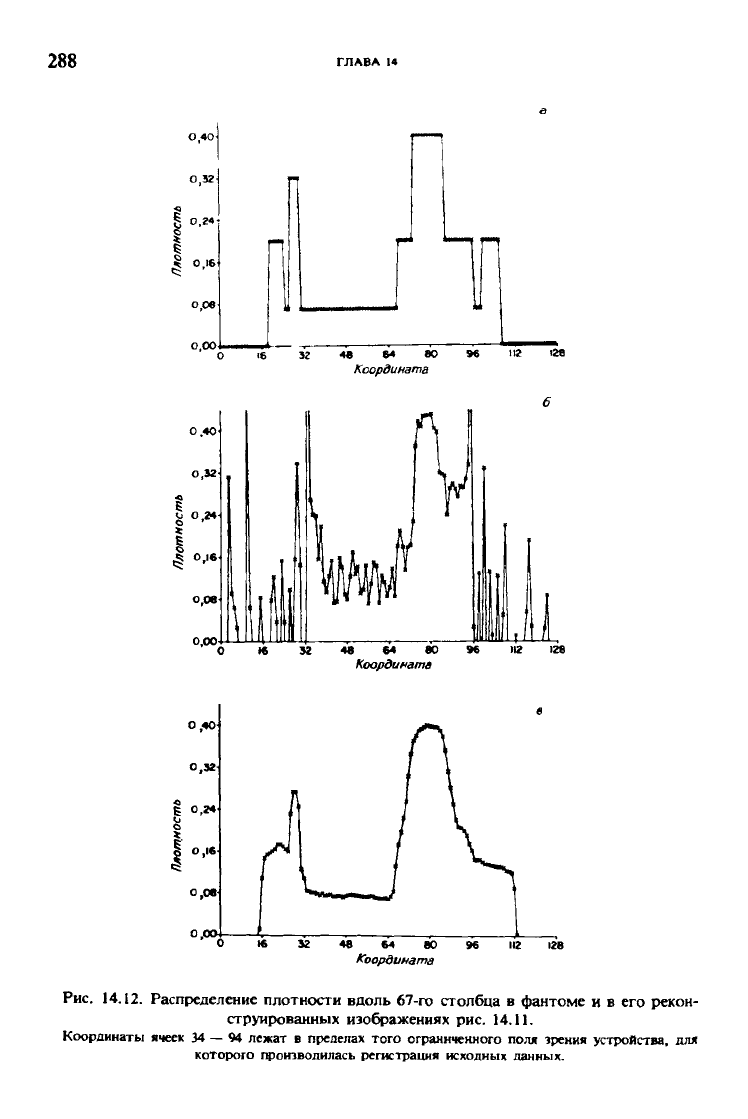
Рис. 14.12. Распределение плотности вдоль 67-го столбца в фантоме и в его рекон-

струированных изображениях рис.

14.11.

Координаты ячеек 34 — 94 лежат в пределах того ограннченного поля зрения устройства, для

которого производилась регистрация исходных данных.

РЕКОНСТРУКЦИЯ ИЗОБРАЖЕНИЯ ТРЕХМЕРНОГО ОБЪЕКТА

289

48 64 80 96

Координата

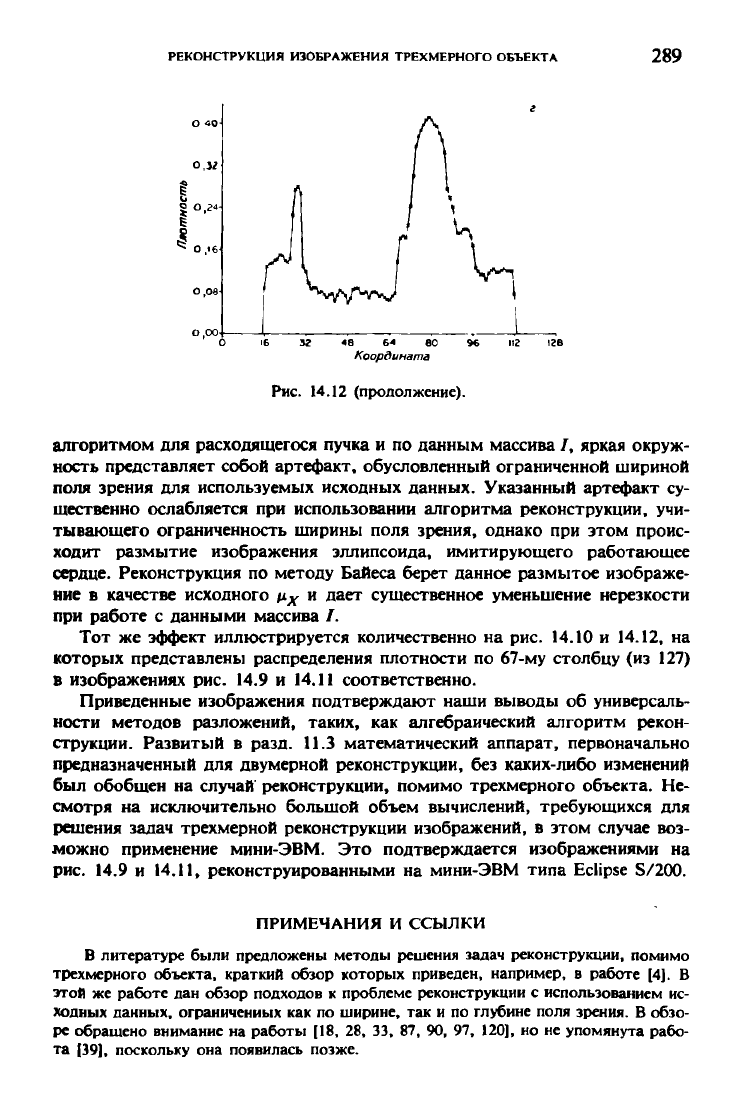
Рис. 14.12 (продолжение).

алгоритмом для расходящегося пучка и по данным массива /, яркая окруж-

ность представляет собой артефакт, обусловленный ограниченной шириной

поля зрения для используемых исходных данных. Указанный артефакт су-

щественно ослабляется при использовании алгоритма реконструкции, учи-

тывающего ограниченность ширины поля зрения, однако при этом проис-

ходит размытие изображения эллипсоида, имитирующего работающее

сердце. Реконструкция по методу Байеса берет данное размытое изображе-

ние в качестве исходного \к

и дает существенное уменьшение нерезкости

при работе с данными массива /.

Тот же эффект иллюстрируется количественно на рис. 14.10 и 14.12, на

которых представлены распределения плотности по 67-му столбцу (из 127)

в изображениях рис. 14.9 и 14.11 соответственно.

Приведенные изображения подтверждают наши выводы об универсаль-

ности методов разложений, таких, как алгебраический алгоритм рекон-

струкции. Развитый в разд. 11.3 математический аппарат, первоначально

предназначенный для двумерной реконструкции, без каких-либо изменений

был обобщен на случай' реконструкции, помимо трехмерного объекта. Не-

смотря на исключительно большой объем вычислений, требующихся для

решения задач трехмерной реконструкции изображений, в этом случае воз-

можно применение мини-ЭВМ. Это подтверждается изображениями на

рис. 14.9 и

14.11,

реконструированными на мини-ЭВМ типа Eclipse S/200.

ПРИМЕЧАНИЯ И ССЫЛКИ

В литературе были предложены методы решения задач реконструкции, помимо

трехмерного объекта, краткий обзор которых приведен, например, в работе [4]. В

этой же работе дан обзор подходов к проблеме реконструкции с использованием ис-

ходных данных, ограниченных как по ширине, так и по глубине поля зрения. В обзо-

ре обращено внимание на работы [18, 28, 33, 87, 90, 97, 120], но не упомянута рабо-

та [391, поскольку она появилась позже.

290

ГЛАВА 14

Описанный в разд. 14.2 метод основан на работе [3]. Методы получения фанто-

мов н проекций основаны на результатах работы [5], в которой приведено описание

наиболее раннего варианта системы (без динамических вариаций). Детальное описа-

ние динамического пространственного реконструктора, а также обсуждение особен-

ностей его применения в физиологии и медицине дано в

[157].

Основанный на байесовском критерии оптимальности алгоритм позаимствован

из работы [6]. Использованный нами метод расширения поля зрения по исходным

данным взят из работы

[108].

Детальный анализ применения сверхбыстродействую-

щего устройства реализации алгоритма для ДПР, названного нами «стационарным

алгоритмом сверточного типа для расходящегося пучка», приведен в работе [46].

Трехмерное отображение

отдельных органов человеческого тела

В предыдущей главе были обсуждены методы, которые могут исполь-

зоваться для получения трехмерного массива данных, представляющих со-

бой средние значения плотностей (или относительных коэффициентов ли-

нейного поглощения) рентгеновского излучения внутри элементарного объ-

ема, расположенного в определенной точке пространства. Даже применяя

алгоритмы реконструкции двумерных изображений и получая набор рекон-

струированных томограмм, можно сформировать трехмерный массив дан-

ных, содержащих пространственную информацию об объекте, а не только

информацию о его поперечных сечениях.

Имея подобный массив трехмерных данных, нетрудно отобразить лю-

бое саггитальное или корональное сечение тела (рис. 2.2), а используя про-

цедуру линейной интерполяции данных, можно рассчитать значения плот-

ности в произвольных точках тела и получить таким образом изображения

срезов в объекте для любой ориентации. Подобный метод достаточно

прост по своей идее, и, хотя он может потребовать разумного подхода при

работе с большими массивами на мини-ЭВМ, в книге подробно рассматри-

ваться не будет.

Вместо этого мы сосредоточим свое внимание на методах, которые по

трехмерному массиву данных позволяют отображать отдельные органы

человеческого тела <так, как если бы эти органы удалены из последнего.

Этот эффект достигается вычислительными средствами, причем вначале

определяют поверхность интересующего органа человеческого тела, а за-

тем отображают его на экране. Комбинацию реконструктивной томогра-

фии с подобной техникой отображения можно назвать «хирургией без вме-

шательства».

15.1.

ОСНОВНЫЕ ПРИНЦИПЫ

Предположим, что интересующая нас область подразделена на элемен-

тарные объемы по методу, аналогичному методу трехмерной дискретиза-

ции разд. 13.1, причем каждый элементарный объем имеет свое число Ха-

унсфилда, аналогичное величине х. в формуле (14.5).

Кроме того, предположим, что трехмерный массив показателей плот-

ности исследуемого органа человека можно отличить от показателей окру-

жающих тканей. Это можно сделать следующим образом: пусть существу-

ГЛАВА 15

РИС.

15.1.

а — реконструированные изображения желудочков мозга выглядят на рисунках более темными,

чем окружающие ткани; б — все элементарные ячейки, имеющие числа Хаунсфилда, близкие к

соответствующим числам для желудочков, белые, все остальные черные.

ет laxort диапазон & значений, число Хаунсфилда внутри органа лежит в

диапазоне <^, а вне его не лежит. Заметим, что элементарный объем либо

находится полностью внутри органа, либо полностью вне его; поэтому

точность представления органов будет определяться размерами элементар-

ных объемов. Из данного определения следует (в рамках исследуемого

приближения), что орган человека состоит из поверхностей, которые разде-

ляют элементарные объемы на два класса, один из которых лежит вне, а

другой — внутри органа.

Примером данного определения может служить рис. 15.1,д, на котором

показаны соответствующие фрагменты трех реконструированных томо-

грамм головы человека, содержащие часть системы желудочков мозга.

Диапазон

выбран

так, что элементарные объемы внутри области желу-

дочков имеют числа Хаунсфилда, лежащие в диапазоне &\ а элементарные

объемы вне этой области имеют числа Хаунсфилда, которые не принадле-

жат диапазону &. На рис. 15.1,6 первые из упомянутых элементарных объ-

емов изображены светлыми, а вторые

—

темными полями.

ТРЕХМЕРНОЕ ОТОБРАЖЕНИЕ ОТДЕЛЬНЫХ ОРГАНОВ

293

Таким образом, мы определили подмножество В элементарных объе-

мов,

в которое входят все элементарные объемы, числа Хаунсфилда для

которых находятся в пределах диапазона &. Интуитивно мы предполагаем,

что «орган» представляет собой подмножество В, которое является в неко-

тором смысле связанным. В следующем разделе мы дадим более точное

определение этому понятию и рассмотрим алгоритмы нахождения границ

органов. Отметим, что органы могут иметь сложные, многосвязные, гра-

ничные поверхности; например, мышца сердца имеет как внешнюю, так и

несколько внутренних поверхностей — по одной на каждую полость серд-

ца.

15.2.

МЕТОДЫ ОПРЕДЕЛЕНИЯ ГРАНИЦ ОРГАНОВ

Обозначим, как и ранее, через J полное число элементарных объемов, а

сами объемы пронумеруем целыми

числами

у,

где

^ j ^ J. Для двух раз-

личных элементарных объемов с индексами j и к будем использовать обо-

значение

/(/, /с), если данные объемы имеют общие грани, или обозначение

e(j

к), если они имеют общее ребро, но не имеют общих граней. В первом

случае будем называть пару элементарных объемов (/', к) гранью объекта, а

пару (/, ( )

—

ребром грани (/, к), если имеются объемы с е (/', f )

/ (/ .

I) (рис. 15.2). Если имеется/(/, *). то мы также говорим, что пара (/', к)

является гранью элементарного объема у. Ясно, что каждый элементарный

объем имеет шесть граней, а каждая грань — четыре ребра. Отметим, что

по причинам, которые станут понятными ниже, мы не будем отождест-

влять грани с (/, к) и (к,

у").

Пусть В и W — два непересекающихся множества элементарных объе-

мов.

Границу

Р(В,

W) между В и W определим как множество граней меж-

ду двумя элементарными объемами, один из которых принадлежит мно-

жеству W. Математически это означает, что

Р(В. W) - {(/>, w)\b

В. \\ е W и f(b.

*•)}.

(15.1)

При этом нас особо не интересуют границы между произвольными мно-

жествами элементарных объемов, поскольку мы ограничимся определени-

ем границ между «рассматриваемым» и «смежным» органами. Определим

теперь смысл введенных понятий.

Для этого обратимся к множеству Q. Интуитивно читатель может.по-

считать, что Q — множество элементарных объемов, значения чисел Хаунс-

филда которых попадают в диапазон значений & (разд. 15.1). например,

если множество Q содержит все элементарные объемы, имеющие одинако-

вую плотность с мышцей сердца (которая по предположению отличается

от плотности крови), то последняя будет «органом» на множестве Q, а

каждая полость сердца (и внешние соединительные ткани) будут «соседним

органом» на Q. Наложим некоторые ограничения на интересующие нас

294

ГЛАВА 15

Рис. 15.2. Пара (у, к) описывает грань элементарного объема

у,

пара (у, /)

—

его

ребро.

множества Q. Во-первых, потребуем, чтобы множество Q было непустым;

во-вторых, Q не должно содержать элементарных объемов, расположен-

ных на границе, другими словами, Q должно быть подмножеством внут-

ренних объемов, обозначаемых в двумерном случае символом N

(разд.

12.3). Вот почему мы будем называть множество элементарных объ-

емов,

удовлетворяющих этим двум условиям,

внутренним

множеством.

Причиной введения второго ограничения является то, что при определении

понятия границы с помощью выражения (15.1) нам были необходимы эле-

ментарные объемы по обе стороны от граничных граней. Второе условие

всегда можно выполнить путем дополнения массива элементарных объе-

мов вспомогательным слоем объемов со всех сторон и присваивания им чи-

сел Хаунсфилда, которые не попадают в диапазон <^.

Пусть Q — внутреннее множество, а В — непустое его подмножество;

при этом будем говорить, что В есть «орган» из Q, если

а) для всех отличающихся друг от друга элементов у и к на подмно-

жестве В существует последовательность f

элементарных объе-

мов,

для которой t

= у, I

= к, и, кроме того, при условии 1 ^ v < и

существует либо пара/( f*. i

v +

*), либо пара е( t

v +

*);

б) подмножество В не является собственно подмножеством любого под-

множества множества Q, которое удовлетворяло бы условию «а».

Проще говоря, «орган» В из Q определяется любым одним из элемен-

тов

следующим образом: «орган» В содержит все элементарные объемы

к, которые можно достигнуть

из

у-го элементарного объема путем пересе-

чения граней и ребер элементарных объемов, принадлежащих множеству

Q. Рис. 15.3 иллюстрирует данное определение.

Пусть Q — внутреннее множество, а В — непустое множество элемен-

тарных объемов, не содержащее ни одного элемента из Q. Другими слова-

ми,

—

подмножество из дополнения Q множества Q. В этом случае мы

говорим, что W является

«смежным

органом» множества Q, если

а) для всех отличающихся друг от друга элементов

в у

и * множества В

на нем существует последовательность t

(

элементарных объемов,

для которой О = у, i

- к, и, кроме того, при условии 1 ^ v < и су-

ществует пара/(

* ') или е( t

, t

v +

>);

б) подмножество В не является собственно подмножеством любого под-

множества Q, которое удовлетворяет первому условию.

ТРЕХМЕРНОЕ ОТОБРАЖЕНИЕ ОТДЕЛЬНЫХ ОРГАНОВ

295

Рис. 15.3. Иллюстрация предлагаемой концепции «органа» и «смежного органа».

Представлены изображения трех последовательно взятых слоев нз трехмерного массива данных.

Неэаштрихованные клетки соответствуют элементарным объемам множества Q. Мы предпола-

гаем,

что все элементы объема, не показанные на рисунке, принадлежат множеству Q. В этом

случае множество Q содержит два «органа», один нз которых состоит нз одного элемента объе-

ма, расположенного в верхнем левом углу правого рисунка, а другой содержит все оставшиеся

элементы множества Q. Множество Q имеет два «смежных органа», один из которых состоит

из двух элементов объема, расположенных в центре среднего рисунка н заштрихованных пере-

крестной штриховкой, а другой — из всех оставшихся элементов множества О.

Проше говоря, «смежный орган» W множества Q определяется одним

из его элементов j следующим образом: «смежный орган» W содержит все

элементарные объемы к

которые можно достигнуть из ./-го элементарного

объема путем пересечения граней элементарных объемов, не принадлежа-

щих множеству Q. Данное определение также иллюстрируется рис. 15.3.

Заметим, что понятие «смежного органа» определено «сильнее», чем

понятие «органов», поскольку в первом случае не допускается связности по

ребрам. Причина этого состоит в том, что нам желательно получить по-

верхность в виде жордановой поверхности, другими словами, в виде по-

верхности, разделяющей пространство на две области с общей границей.

называемые внешней и внутренней оЬ/шстями соответственно. [В нашем

случае поверхностные элементы представляют собой пары элементарных

объемов ф, и>), где b — внешняя, aw — внутренняя области. Заметим, что

полное значение понятия «внутренняя область» определяется как «внутрен-

няя область органа». Весьма вероятно, что внутренняя область может за-

ключать в себе внешнюю, как это было в приведенном примере с мышцей

сердца и его полостями.] Кроме того, каждая точка пространства, не лежа-

щая на жордановой поверхности, должна принадлежать либо внутренней,

либо внешней области. Любые две точки во внутренней (или во внешней)

области можно соединить кривой, не содержащей точек поверхности. Лю-

бая кривая, соединяющая точки внутренней и внешней областей, должна

содержать по крайней мере одну точку поверхности. В частности, полупря-

мая,

берущая свое начало в точке внутри поверхности, не может выйти из

внутренней области, ие пересекая поверхности. Ниже мы широко использу-

ем данное свойство.

Цель настоящего раздела — найти такой алгоритм, который для любо-

го внутреннего множества Q и для 1юбой пары элементов ф, w) границы

296

ГЛАВА IS

P(Q, Q) давал бы нам все элементы множества Р(В, W), где В характери-

зует «орган» из Q, который содержит объем b, a w характеризует «смеж-

ный орган» из Q

который содержит объем и\ Проще говоря, алгоритм

должен давать способ нахождения всех граней на границе (или на ее части)

«органа», который содержит данную поверхность.

Предположим, что мы имеем метод, с помощью которого для любого

внутреннего множества у, любых «органов» В и «смежных «органов» и/,

принадлежащих Q, и для любой поверхности г, лежащей на границе Р(В,

на ней образовывались бы две другие грани

/,(/■)

(г),

для которых

было бы справедливо следующее утверждение: для всех граней р и q, от-

личающихся друг от друга на границе

Р(В

W), на ней существует последо-

вательность граней г

, ... , /*, для которой г

= p

г" = q

и, кроме того,

при условии 1 ^ v < и существует либо грань г" +

/^г

либо грань

+ !

f-$f}-

Подобный метод можно применить в качестве алгоритма

определения граничных поверхностей,

объяснению которого мы и перехо-

дим.

Данный алгоритм дает «перечень» L граней и использует «соединение»

Р граней. Предположим, что пара объемов (Ь,

и>)

— заданная на границе

грань P(Q, Q). Алгоритм включает в себя следующие операции:

а) подставить (b, w) в L и Я;

б) убрать элемент г из Р;

в) если поверхность/j(г) не содержится в «перечне» L, то необходимо

подставить /

(г) в £ иР;

г) если поверхность /

(г) не содержится в «перечне» L, то необходимо

подставить /

(г) в L и Р\

д) если множество Р пустое, то вычисления заканчивают; в противном

случае переходят к выполнению операции «6».

Теперь рассмотрим особенности предложенного алгоритма. Прежде

всего мы предполагаем существование метода, позволяющего получать

функции /j(r)

(г) для любой грани г на границе Р(В,

IV),

причем г, вы-

числяемое по «6», принадлежит границе

Р(В,

W), поскольку она принадле-

жит множеству Я. Легко показать, что на любом этапе выполнения алго-

ритма все элементы множества Р содержатся в Р(В, W). Аналогично все

элементы «перечня» L также содержатся в Р(В, W), и благодаря специфи-

ческим свойствам

функций

любой элемент, принадлежащий

Р(В,

W),

рано или поздно попадает в L. С этого момента множество Р исчерпыва-

ют повторением операции «б», не распространяя алгоритм на операции

«в» и «г». Таким образом, множество при определенных обстоятельствах

оказывается пустым, и с этого момента выполнение алгоритма прекраща-

ется на том «перечне» L, который содержит все элементы границы Р{В,

W) и не содержит никаких других.

Таким образом, алгоритм позволяет выполнить поставленную перед

ним задачу. Единственное, что было здесь опущено, — это объяснение то-

го,

как по грани г рассчитать /

{

{г)

(г).

Хотя этот вопрос и весьма су-

ществен, из-за технических трудностей его подробное изложение в настоя-

щей книге опущено. Здесь на примере «органа», состоящего из трех эле-

ТРЕХМЕРНОЕ ОТОБРАЖЕНИЕ ОТДЕЛЬНЫХ ОРГАНОВ

297

12 9

РИС.

15.4.

а — «орган», содержащий три элементарных объема; б — связанные с ним функции /| (сплош-

ные стрелки) и /

(штриховые стрелки), осуществляющие отображение поверхности на поверх-

ность.

ментарных объемов, мы приведем простую иллюстрацию возможностей

метода.

На рис. 15.4 изображены три элементарных объема, которые по пред-

положению принадлежат множеству Q

а остальные объемы — множеству

Q. Все поверхности на границе

Р(В,

W) пронумерованы цифрами 1 — 14, и

мы будем считать, что заданная поверхность имеет номер 1.

Функции

определяются с помощью графа рис. 15.4,6, причем грань г соединяется

с гранью f

{r) сплошной стрелкой, а с гранью /

(г) — штриховой. Доста-

точно просто, но очень громоздко провести доказательство того» что ука-

занные

функции

{

действительно обладают требуемыми свойствами.

Теперь мы продемонстрируем работоспособность алгоритма при помо-

щи таблицы. В каждой строке табл. 15.1 последовательно приведены зна-

чения величин г, Р и L на пятом этапе вычислений.

На практике может потребоваться слишком много времени для провер-

ки на третьем и четвертом этапах вычислений того, содержатся или нет

грани f

(r) и f£r) в «перечне» L. Последнее обусловлено тем, что множе-

ство Р(В, W) может содержать около

000 элементов (мы увидим это на

примере разд. 15.5), а множество L при определенных обстоятельствах

может иметь такое же число элементов.

Один иэ методов уменьшения количества требуемых вычислений для

определения того, принадлежит ли уже поверхность «перечню» Z,, состоит

в разбиении L на несколько «перечней» меньшего размера в зависимости от

специфических свойств его элементов. При этом каждую новую грань по-

требуется проверять лишь в одной какой-либо группе. Например, все грани

ориентированы в одном из шести возможных направлений (т.е. для граней

с индексами (/, к) вектор, восставленный из

центра

у-го

элементарного объ-