Хермен Г. Восстановление изображений по проекциям: Основы реконструктивной томографии

Подождите немного. Документ загружается.

278 ГЛАВА 14

Рис. 14.5. Проекции фантома грудной клетки, полученные в один и тот же момент

времени при четырех различных положениях источника.

Необходимо отметить, что из-за больших размеров фантома в поле зрения системы изображе-

ния попадает лишь часть фантома.

поворотом рамы ДПР на угол 1,5° от выборки к выборке. Таким образом,

угловое расстояние между положениями «первого» рентгеновского источ-

ника при первой временнбй выборке и «последнего» источника при послед-

ней временнбй выборке также равно 1,5° (рис. 14.4). Другими словами, все

240 положений занимаются в процессе моделирования по крайней мере

один раз одним из 28 источников. Общая продолжительность моделируе-

мого на ДПР процесса равна 2,1833 с; в течение этого времени интеграль-

ные значения плотности регистрируются на 29571696 линиях (132 времен-

ные выборки ж 28 источников ж 63 строки х 127 точек отсчета). Каждый

из упомянутых интегралов вычисляется с учетом положения эллипсоидов

за достаточно малое время. Для имитации статистического характера ре-

гистрации рентгеновских данных к значениям линейных интегралов добав-

лялась случайная шумовая компонента с гауссовым распределением вероят-

ности и нулевым средним значением.

Конечной целью применения в ДПР алгоритмов реконструкции являет-

ся вычисление изменяющегося во времени трехмерного распределения

плотности по коническим рентгеновским проекциям, зарегистрированным в

течение всего времени.

РЕКОНСТРУКЦИЯ ИЗОБРАЖЕНИЯ ТРЕХМЕРНОГО ОБЪЕКТА 279

Рис.

14.6. Проекции фантома грудной клетки, полученные за четыре момента време-

ни при фиксированном положении источника.

На рис. 14.5 приведены проекции фантома, полученные в один и тот же

момент времени при четырех различных положениях источника, а на рис.

14.6 — проекции фантома при фиксированном положении источника за че-

тыре различных момента времени.

Для наших экспериментов из всех рассчитанных линейных интегралов

были получены два массива данных: А (усредненный) и / (мгновенный).

Массив А содержит 240 усредненных по времени проекций. В процессе

моделирования каждое из 240 возможных положений источника (рис, 14.4)

занимается по крайней мере один, но не более 28 раз, хотя и в различные

моменты времени. При формировании массива А для каждого положения

источника рассчитывались одиночные усредненные проекции, состоящие из

127 точек отсчета в каждой из 63 строк, что осуществлялось путем усредне-

ния всех проекций, полученных в данном положении источника. Таким об-

разом, массив А состоял из 1920240 элементов (240 положений источни-

ка х 63 строки х 127 точек отсчета).

Массив / содержит данные, зарегистрированные в отдельные моменты

времени, и состоит из 224048 элементов (28 источников х 63 строки х 127

точек отсчета).

Учитывая очевидные преимущества сверточного алгоритма для веерно-

го пучка (гл. 10), было сочтено целесообразным применять этот алгоритм

280

ГЛАВА 14

1 2

=1^

^^D

■^^ _ -»-*

"^^^^

"-"""^^i

^^w+^s?

^^D

Рис. 14.7. Соотношение между проецированием с помощью конических и веерных

пучков.

В динамическом пространственном реконструкторе заданный рентгеновский источник S проеци-

рует исследуемый объем / на регистрирующий экран 2 с помошью конического пучка. Линия на

экране, на середине которой находится точка D, параллельна плоскости кругового перемещения

рентгеновского источника 3 и характеризует поперечное сечение объекта, изображенное на рисун-

ке штриховой линией, которое оказывается наклонным, т.е. не параллельным плоскости переме-

щения источника. Точки данного сечения проецируются иа линию, содержащую точку D. При

различных положениях источника различные наклонные сечения объекта будут проецироваться

на линии, находящиеся на одном н том же уровне экрана. Однако все указанные наклонные сече-

ния проходят через точку О, которая лежит на оси вращения рамы ДПР. Рассмотрим попереч-

ное сечение объекта, параллельное плоскости перемещения источника и содержащее точку О (об-

ведено иа рисунке сплошной жирной линией). В качестве начального приближения можно счи-

тать,

что все исходные данные, зарегистрированные на экране на уровне точки D, получены с ис-

пользованием веерного рентгеновского пучка, проходящего через сечение, содержащее точку О и

параллельное плоскости перемещения источника. Реконструированные изображения, полученные

с использованием данного предположения, могут быть частично смазаны в направлении, перпен-

дикулярном плоскости перемещения источника.

к обработке массива /. Используемая конфигурация системы регистрации

данных ДПР с одинаковыми временными выборками, к сожалению, не по-

зволяет удовлетворить исходным предположениям, которые были сделаны

при разработке сверточных алгоритмов реконструкции для веерного пучка,

в силу следующих трех причин:

а) рентгеновский пучок является коническим, а не веерным; рентгенов-

ские лучи распространяются не в плоскостях, параллельных плоскости

окружности, на которой расположены источники;

б) в любой заданный момент времени рентгеновский источник располо-

жен на дуге 162°, а не на всей окружности 360°. Другими словами, теперь

система обладает ограниченной глубиной поля зрения; заметим также, что

данное условие противоречит предположениям, сделанным в разд. 14.2;

РЕКОНСТРУКЦИЯ ИЗОБРАЖЕНИЯ ТРЕХМЕРНОГО ОБЪЕКТА 281

в) из-за конечных размеров изображающей системы часть тела выпада-

ет за пределы конуса рентгеновских лучей (этот эффект заметен на рис.

14J

и 14.6), и, таким образом, система обладает ограниченным полем зре-

ния.

Суммарный эффект, имеющий место из-за несоответствия конфигура-

ции системы регистрации исходных данных и использованных при разра-

ботке алгоритма предположений, состоит в том, что реконструированные

в ДПР изображения стационарных объектов, полученные с помощью свер-

точного алгоритма для веерного пучка, гораздо, хуже по качеству обычно

получаемых изображений одиночных поперечных сечений в сканерах рекон-

структивных томографов. Последнее усугубляется тем, что для получения

одиночных временных выборок в ДПР берется лишь 28 положений источ-

ника, тогда как в сканерах с одиночным регистрируемым поперечным сече-

нием вращающийся источник рентгеновских лучей в процессе получения ис-

ходных данных для реконструкции данных занимает 288 и более положе-

ний.

На рис. 14.7 показано, каким образом проекцию, полученную с по-

мощью конического пучка, можно свести к набору эквивалентных проек-

ций, зарегистрированных в веерных пучках. Качество реконструированных

изображений, полученных с применением к массиву / алгоритма, справед-

ливого для веерного пучка, будет продемонстрировано ниже.

14.4.

АЛГОРИТМ ТРЕХМЕРНОЙ РЕКОНСТРУКЦИИ,

ОСНОВАННЫЙ НА ПРОЦЕДУРЕ БАЙЕСОВСКОЙ ОПТИМИЗАЦИИ

Перейдем теперь к рассмотрению такого алгоритма реконструкции, ко-

торый не требует при выводе использования заведомо неверных (или приб-

лиженно справедливых) предположений о конфигурации ДПР. При этом

мы произведем существенное заимствование материала из разд. 11.3, в ко-

тором описан аналогичный алгоритм реконструкции поперечных сечений, а

именно аддитивный алгебраический алгоритм реконструкции, предназна-

ченный для получения байесовской оценки, минимизирующей соотношение

(11.26).

Предположим, что реконструкция трехмерного объекта производится в

отдельные моменты времени, а функция / описывает данный эффект. В на-

стоящем разделе в качестве элементарных объектов будут использоваться

объекты, определяемые в соответствии с формулой (14.4). Таким образом,

Функция

/ будет представлять собой /-мерный вектор изображения х, где

равно среднему значению / в пределах у-го элемента объема.

Для эффективного использования данного представления необходимо,

чтобы размеры элементов объема были малы, поэтому число компонент

вектора х должно быть достаточно велико. Что касается использованного

нами фантома, то он состоял из слоев элементарных объемов, параллель-

ных плоскости вращения источников. В каждом слое содержалось

282 ГЛАВА 14

127 х 127 элементарных объемов для «заполнения» всей грудной клетки,

причем для «заполнения» миокарда требовалось 63 слоя. В своей работе

мы использовали лишь 39 центральных слоев, которые «заполняли» ббль-

шую часть левого желудочка. Таким образом, вектор * имел 629031 компо-

ненту (39 слоев из 127 х 127 элементарных объемов) в любой момент вре-

мени. Целью применений алгоритма реконструкции является вычисление

вектора х по имеющимся исходным данным, причем для реконструкции

одного полного цикла сокращения сердца требуется около 60 последова-

тельных временных Выборок!

В разд. 11.3 было показано, что при определенных предположениях,

описываемых соотношениями (11.38) и (11.39), алгоритм дает последова-

тельность векторов, сходящихся к байесовской оценке х

. Тот же алгоритм

в принципе можно использовать и в случае конического пучка.

Необходимо заметить, что, несмотря на чрезвычайно большой объем

вычислений (в нашем случае вектор х имеет около полумиллиона компонент),

рассмотренный алгоритм применим даже для расчетов на мини-ЭВМ, что

возможно благодаря учету главных геометрических особенностей задачи.

Детали вычислений мы опускаем, но предупреждаем неискушенного чита-

теля о том, что практическая реализация данного алгоритма в значитель-

ной степени зависит от организации в ЭВМ массивов данных, содержащих

значения х^

\ у и ы

(/г)

(вектор R вообще не требует запоминания, поскольку

его компоненты вычисляются по мере надобности). На практике для

уменьшения числа обращений к дисковой памяти использовался слегка из-

мененный вариант указанного алгоритма.

Отметим, что данный алгоритм применяется в сочетании с конической

конфигурацией системы регистрации исходных данных и подтверждается

теорией, даже несмотря на то, что источники располагаются на дуге всего

162° и часть объекта выпадает из конуса рентгеновских лучей. С другой

стороны, теория основывается на предположении о гауссовом законе рас-

пределения случайных величин X -

иЕ

(разд. 11.3), которые, вероятно,

на практике нарушаются, однако, несмотря на это, получающаяся схема

нахождения оценки математически привлекательна.

Другой важный вопрос, который до сих пор не затрагивался, относится

к выбору ожидаемых значений ^игв формуле (11.26)

Вектор изображения х представляет собой выборки случайной функции

с математическим ожиданием \х

. Массив А формировался путем усредне-

ния по времени проекций, что подтверждает целесообразность реконструк-

ции изображения с использованием массива А в качестве вектора ц

Массив А содержит 240 проекций, полученных в конических пучках для

случая, когда источник занимает ряд положений на окружности; поэтому

возражения относительно ограничения глубины поля зрения к массиву А не

относятся. Использование алгоритма, который применим для веерного

пучка, приводит к возникновению размытости между отдельными срезами

(рис. 14.7), что приемлемо для наблюдаемого изображения. Единственное

оставшееся возражение против использования алгоритма реконструкции

РЕКОНСТРУКЦИЯ ИЗОБРАЖЕНИЯ ТРЕХМЕРНОГО ОБЪЕКТА

283

сверточного типа для веерного пучка состоит в том, что исходные данные

имеют ограниченную ширину поля зрения.

К счастью, существуют эффективные алгоритмы предварительной об-

работки исходных данных с ограниченной шириной поля зрения, что позво-

ляет применить к ним алгоритм реконструкции сверточного типа для веер-

ного пучка. Мы выбрали один из этих алгоритмов, который предусматри-

вает проведение следующих операций.

Для каждого положения источника проекции, полученные в расходя-

щемся пучке, дополняются с обеих сторон значениями лучевых сумм на до-

полнительных лучах, так что область реконструкции после дополнения ока-

зывается заключенной между двумя крайними лучами. Лучевые суммы на

дополнительных лучах принимаются равными линейным интегралам

(вдоль луча) для диска с постоянной плотностью и с центром, совпадаю-

щим с началом координат. Плотность в упомянутом диске вычисляется

раздельно для различных краев дополненной проекции, причем значение на

одном краю проекции наилучшим образом (в смысле, определяемом по ме-

тоду наименьших квадратов) сопряжено со значениями лучевых сумм, пер-

воначально измеренных на пяти крайних лучах. Как можно будет убедить-

ся ниже, даже такая довольно грубая экстраполяция дает реконструирован-

ные изображения приемлемого качества.

Преобразуя полученный в коническом пучке массив А во множество

данных веерного типа (как это указано на рис. 14.7) и дополняя указанные

данные по слоям, чтобы избежать эффектов ограничения ширины поля зре-

ния,

можно при использовании сверточного алгоритма для расходящегося

пучка (разд. 10.1) получить величину ц

слой за слоем.

Величину г можно оценить при помощи фантома (или фантомов) для х

аналогично тому, как мы пытались реконструировать и определяли

г = г

Л,

где / — стандартное отклонение компонент вектора х

—

, а

s — стандартное отклонение компонент вектора у

—

Rx.

14.5.

НАГЛЯДНЫЕ ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ АЛГОРИТМОВ

Данные массивов А и I были использованы для реконструкции изобра-

жений. Вначале для получения величин ц

из массива А были взяты 39

групп данных, каждая из которых характеризовала отдельный слой рекон-

струированного объекта. Для каждого из 240 положений источника дела-

лась выборка с соответствующей строки, как это показано на рис. 14.7. Та-

ким образом, величина ц

определялась по 39 отдельным ракурсам с огра-

ниченным полем зрения при помощи алгоритмов реконструкции сверточно-

го типа для веерного пучка. Для каждого ракурса значения рассчитывались

в 16129 точках (127 х 127 центров элементарных объемов) по 30480 значе-

ниям (240 положений источника х 127 выборок для каждого из них).

Было установлено, что для объекта данного типа и данной погрешно-

сти измерений, которые имели место в нашем эксперименте, величина

284

ГЛАВА 14 V

Рис. 14.8. Проекция фантома грудной клетки с нанесенными на нее линиями на уров-

не 22-Й и 42-й строк изображения (общее число строк на экране 63).

г = 0,8 является приемлемой. Теперь, имея значения ц

и г, остается «все-

го лишь» найти оценку **, минимизирующую соотношение (11.26), в кото-

ром в качестве вектора измерений у взят массив /. Напомним, что число

компонент у векторов х и у равно 629031 и 224028 соответственно.

Несмотря на это, был применен алгоритм, описанный в предыдущем

разделе. Был выбран постоянный параметр релаксации X*** = 0,5. Алго-

ритм применялся к исходным данным в течение трех полных циклов итера-

ций,

а разница между оценками функции объекта в конце второго и третье-

го циклов итерации оказалась пренебрежимо малой, поэтому было сочтено

целесообразным ограничиться тремя итерациями. Перейдем теперь к рас-

смотрению полученных результатов.

На рис. 14.8 представлено изображение проекции с нанесенными на него

двумя линиями, которые показывают различные положения линии, середи-

на которых отмечена буквой D на рис. 14.8. На следующих рисунках будут

приведены соответствующие поперечные сечения объекта, одно из кото-

рых, изображенное на рис. 14.7, параллельно плоскости перемещения ис-

точника с центром в точке О (обведено жирной линией). Для линий, отме-

ченных на рис. 14.8, были получены изображения сечений на уровне 22-й и

42-й строк (первоначально при дискретизации было взято всего 63 строки).

Указанные сечения располагались примерно на 3 см выше и ниже плоско-

сти сканирования источника соответственно (рис. 14.9 — 14.12).

На каждом из рисунков приведены изображения самого фантома (а)>

объекта, реконструированного по данным массива / и стационарного алго-

ритма сверточного типа для расходящегося пучка (б), объекта р

, рекон-

РЕКОНСТРУКЦИЯ ИЗОБРАЖЕНИЯ ТРЕХМЕРНОГО ОБЪЕКТА 285

Рис. 14.9. а

—

распределение плотности в фантоме на уровне 22-Й строки и его ре-

конструированные изображения; данный уровень находится приблизительно на 3 см

выше плоскости перемещения рентгеновского источника; б

—

реконструированное

изображение, выполненное с использованием стационарного сверточного алгоритма

для расходящегося пучка и массива /; в — то же с использованием массива А\

г — то же с использованием алгебраического алгоритма реконструкции и массива /.

струированного по данным массива / и алгоритма сверточного типа для

веерного пучка с ограниченной шириной поля зрения (в) и полученного в

конце третьего цикла итераций по методу Байеса по данным массива (г).

Эффект ограничения глубины поля зрения в методе, который выше мы на-

звали «стационарным алгоритмом сверточного типа для расходящегося

пучка», достигается наиболее простым из возможных способов: «пропу-

щенные» ракурсы попросту игнорируются. Последнее оказывается эквива-

лентным предположению о равенстве нулю лучевых сумм указанных ракур-

сов при последующем использовании формул разд. 10.1. Данные, получен-

ные подобным образом, многократно нормируются, причем число норми-

ровок равно отношению полного числа ракурсов (в нашем случае 60, без

пропусков) к действительному числу ракурсов, равному 28. Каждое сечение

реконструируется независимо по частичному массиву / в соответствии с ме-

тодом, изложенном в подписи к рис. 14.7.

На рис. 14.9 и 14.11 изображен внешний вид сечений, взятых на уровне

22-го и 42-го слоев соответственно. Величины плотности фантома, присва-

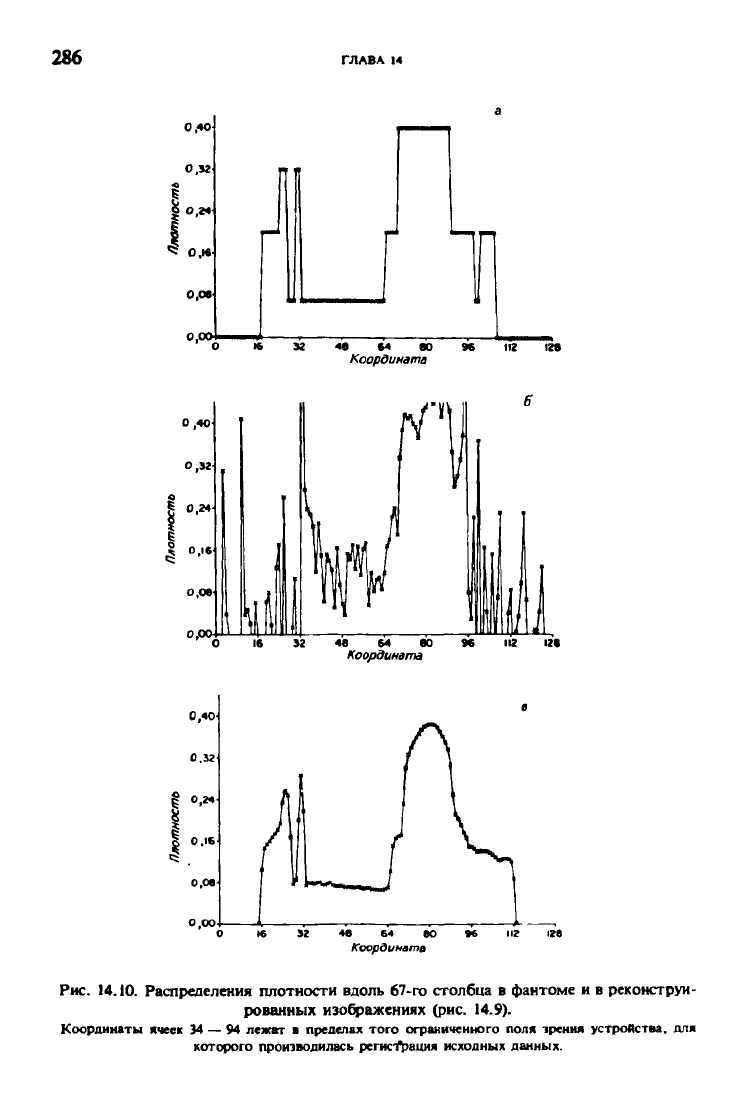
286

ГЛАВА 14

0,40

О 0,241

^ 0,1б|

0,00-

в «4 80

Координата

н2 iza

Координата

Рис. 14.10. Распрелеления плотности вдоль 67-го столбца в фантоме и в реконструи-

рованных изображениях (рис. 14.9).

Координаты ячеек 34

—

94 лежат в пределах того ограниченного поля зрения устройства, для

которого производилась регистрация исходных данных.

РЕКОНСТРУКЦИЯ ИЗОБРАЖЕНИЯ ТРЕХМЕРНОГО ОБЪЕКТА

287

Рис. 14.10 (продолжение).

Рис.

14.11.

Распределение плотности в фантоме на уровне 42-й строки.

Данный уровень находится приблизительно на 3 см ниже плоскости перемещения рентгеновского

источника. Условия регистрации такие же, как н на рис. 14.9.

иваемые данным элементарным объектам, равны значениям плотности в

центрах этих объектов. В изображении, реконструированном сверточным