Хермен Г. Восстановление изображений по проекциям: Основы реконструктивной томографии

Подождите немного. Документ загружается.

258

ГЛАВА 13

|0 при к Ф /.

(PXs = |

M(2/V + !)£-/(М + 2к - I)

при к = Л

(1344)

Анализируя результаты данного и предыдущего разделов главы, можно

отметить следующее. Если исходные данные регистрируются вдоль лучей с

параметрами (

, в

п т

, где t

и 0

Л т

удовлетворяют соотношениям

(13.39) и (13.6) соответственно, общее число лучей составляет

/ = M(2N + 1), а

базисных изображений [где

= U(2V + 1)] заданы со-

отношениями (13.34), (13.35) и (13.13), и если 2V + 1 ^ М и

V + 2U - 1 < N, то матрица R

R является диагональной, а ее диагональ-

ные элементы равны (при 1 ^ j ^ J)

= 2HJE

{\ij\ + 2uj + l)

, (13.45)

Здесь величины и- и f определены в соответствии с формулой (13.10).

Теперь обсудим вопрос о том, насколько приемлем выбор значений (

по формуле (13.39).

Одна из возможностей состоит в выборе величины у, равной

—

т/2\ при

этом 7о = -*/2 и £

= 0, а в общем случае при -N ^ п ^ N имеем

= E sin|>27r/(27V + 1)]. (13.46)

Поскольку величина ( с изменением п в интервале

—

N ^ п ^ N сначала

уменьшается, потом увеличивается, а затем вновь уменьшается, конфигура-

ция лучей в пучке при одном ракурсе при первом рассмотрении недостаточ-

но понятна. Для выяснения этого вопроса введем множество таких отрез-

ков d

что

0 = d

< d

< <d

< Е, (13.47)

</_* = -d

(13.48)

для 1 ^ к ^ 7V, причем множество значений d

эквивалентно множеству

, поэтому в символической форме записи имеем

\ -N <к< N] = {/J -N <п< N]. (13.49)

Указанное множество отрезков d

определяется выражением

= £ sin[/c7r/(27V + 1)], П3.50)

при —N ^ к ^ N. Доказательство того, что величины d

обладают

свойствами (13.47) и (13.48), достаточно очевидно и вытекает из элементар-

ных свойств синусоиды. Замечая, что

НЕИТЕРАЦИОННЫЕ АЛГОРИТМЫ РЕКОНСТРУКЦИИ

259

sin а = sin(7i - а), (13.51)

нетрудно получить подстановкой а - (2N + 1 - 2\K/(2N + 1), что для

—

N ^ п ^ N справедлива формула

sin[(2N + 1 - 2n)n/(2N + 1)] = sin|>2*/(2yv + 1)]. (13.52)

Из соотношений (13.46) и (13.52) получаем, что при условии I ^ п ^ N

имеем

Л,

= </*, (13.53)

где

|2л

если 1 < п < N/2,

[27V н- 1

—

2и. если N/2<n< N

Отметим, что если п лежит в интервале

- N, то к также лежит в том же

интервале. Справедливость записи (13.49) вытекает из свойства (13.49) и

Таким образом, давая определение £

с помощью соотношения (13.46),

мы получаем множество отрезков, достаточно хорошо покрывающих ин-

тервал значений —

Е,

£. Действительно, из свойств синусоиды легко полу-

чить, что

0<(E-d

)<(d

- d

)<-

■

-d

<d,- d

< (л/(2УУ + 1))£,

(13.55)

откуда следует, что, несмотря на неравномерность выборочных точек £

иа интервале —

Е, расстояние между двумя соседними точками нигде не

превышает более чем в т/2 раз (~ 1,57) расстояние, которое можно полу-

чить при равномерной выборке и том же числе точек отсчета.

Если в какой-либо системе регистрации трудно получить выборочные

значения для множества \ в соответствии с зависимостью (13.46), то за-

регистрированные исходные данные можно подвергнуть операции повтор-

ного разбиения (разд. 10.5), так что и в этом случае можно применять ме-

тод,

рассмотренный в данном разделе.

В частности, функционирование системы регистрации в режиме веерно-

го пучка естественным образом приводит к выбору £ в соответствии с

формулой (13.39). В этом режиме исходные данные регистрируются вдоль

лучей с параметрами (

, 0

л т

) = (D sin лЛ, /лД + rtX), где Д = 2т/М

[соотношение (10.20)]. Если величина X выбрана в соответствии с форму-

лой вида

= rc/(2/V + 1), (13.56)

Для некоторых достаточно больших значений N, то видно, что для указан-

ных лучей величины 0

(при в

п 0

= л Л) и £

удовлетворяют выражени-

П3.6) и (13.50) соответственно в предположении, что Е = D. Другими

260

ГЛАВА 13

словами, если вообразить, что область реконструкции занимает всю внут-

реннюю часть круга, по которому движется источник (рис. 5.2), то величи-

ны (

необходимо выбирать так, как этого требует развитая выше тео-

рия.

Однако при этом нет необходимости использовать лучшее приближе-

ние, поскольку, во-первых, полагая Е = D, мы теряем важную априорную

информацию о том, что функция изображения обращается в нуль вне пер-

воначальной малой области реконструкции. Во-вторых, возникает некото-

рая двусмысленность, обусловленная тем, что величины N в формуле

(13.56) и на рис. 5.2 выбраны неодинаковыми. Используя А" для величины

N на рис. 5.2, видно, что N > N . Для применения алгоритма, описанного

в настоящей главе, необходимо положить равным нулю лучевые суммы

вдоль дополнительных лучей.

13.3.

ПРИМЕНЕНИЕ НЕИТЕРАЦИОННЫХ АЛГОРИТМОЬ

РЕКОНСТРУКЦИИ С РАЗЛОЖЕНИЕМ ФУНКЦИИ В РЯД

При использовании метода разложения изображения на кольцевые гар-

монические составляющие необходимо изменить алгоритм вычислений

разл.

13.1 так, чтобы номер гармоник зависел от положения кольца. Дру-

гими словами, определим положительное целое число V

(0 ^ и ^ U

—

и используем выражение для базисных изображений bj в виде (13.11) лишь

в том случае, когда

—

^ v ^ V

(последнее эквивалентно условию

х. = 0 при \vA > V

). Причины такого подхода состоят в том, что коль-

J J -

ца меньшего радиуса имеют меньшую площадь, и нет необходимости

брать частоту гармоники выше, чем у кольца наибольшего радиуса.

Аналогично при использовании метода полиномиальных разложений не-

обходимо изменить алгоритм вычислений, как это сделано в разд. 13.2, и

взять полиномы R

u v

вплоть до степени 2U, которая, как это определено

выражением (13.35), равна \v\ + 2м. Таким образом, мы вновь определя-

ем положительное целое число У

(а именно равное V

= {2U

—

2и),

O^u^U—

\)н используем выражение для базисных функций b в виде

(13.34) лишь в случае, когда - V

^ v ^ У

Рассмотренные в настоящей главе алгоритмы реконструкции можно ре-

ализовать за три этапа вычислений:

а) расчет величины R

б) решение системы нормальных уравнений (1.31);

в) расчет изображения, основанный на решении системы нормальных

уравнений [соотношение

(6.25)].

Рассмотрим особенности применения методов отдельно для каждого из

этапов.

В принципе произведение R

у состоит из двух сомножителей: /-мерного

вектора и матрицы размерами J х /, вычисление которых на первый

взгляд требует J х / операций умножения. Однако величина r

определя-

НЕИТЕРАЦИОННЫЕ АЛГОРИТМЫ РЕКОНСТРУКЦИИ

261

ется формулой (13.22), поэтому

\ / MI \

y)j=

UjmV

nmm

l (13.57)

где

Рп.т

= У,

(13.58)

обозначает измеренную для луча

параметрами

, в

п т

)

лучевую сумму.

Для фиксированного значения

вычисления внутренней суммы

TMK.JPn.rn

(13.59)

in = 0

при

—

V ^ v ^ V

можно сушественно ускорить путем использования алго-

ритма быстрого преобразования Фурье (БПФ, разд.

9.2),

который подроб-

но рассматривать здесь

не

будем.

Что

касается метода полиномиального

разложения,

котором величины

и v

также определены

помощью гар-

монических функций [соотношение (13.41)],

то и в

этом случае вычисления

внешней суммы могут быть также ускорены

при

помощи

БПФ.

Общий подход двух последних разделов

был

продиктован стремлением

упростить решение системы нормальных уравнений,

и в

этом смысле

ко

второму этапу вычислений добавить нечего.

На третьем этапе

нет

чего-либо такого,

что

могло

бы

беспокоить

нас в

случае, когда базисные изображения получены

помощью дискретизации.

Последнее объясняется тем,

что при

этом выходные данные представляют

собой дискретизованное изображение, пригодное

для

непосредственного

отображения или для выдачи вычисленного значения коэффициента относи-

тельного поглощения

отдельных точках. Теперь

же

складывается совер-

шенно иная ситуация.

При

использовании метода полиномиальных разло-

жений каждое базисное изображение дает вклад

каждую точку рекрнстру-

ированного изображения, поэтому вычисление функции

(г,

ф) для

раз-

личных значений

(г,

ф) становится слишком трудоемким

неэкономичным.

Данная ситуация несколько смягчается

случае применения метода разло-

жения

на

кольцевые гармоники, поскольку для получения значений функции

/ (г, ф) в

фиксированных точках

координатами

(г, ф)

учитывается вклад

лишь 2 V

+ 1

базисных изображений. Достаточно просто вычислить функ-

цию/*

(г,

ф)

сначала

точках, лежащих

на

множестве концентрических

ко-

лец

центром

начале координат,

только потом произвести интерполя-

цию

целью получения дискретизованного изображения.

Это

также позво-

лит

нам

использовать алгоритм

БПФ для

ускорения расчетов, которые

противном случае могут оказаться слишком трудоемкими.

Суть разработанного

разд.

13.2

алгоритма будет прои ыюстрирована

ниже

на

стандартных проекционных данных.

Для

этого

нам

потребуется

ввести дополнительные лучи

нулевыми значениями лучевых сумм, как

это

262

ГЛАВА

было описано в разд. 13.2. Действительно, поскольку в стандартной схеме

реконструкции D > Е, то число рассматриваемых лучей составляет

2N + 1 = 1631, причем лишь 165 центральных лучей имеют измеренные

значения лучевых сумм, а остальным присвоены нулевые значения. Учиты-

вая,

что число ракурсов в стандартных проекциях составляет М = 288,

ограничение числа V обусловливает выбор V ^ 143 [см. материал, пред-

шествующий соотношению (13.45)]. Мы приняли V = 143. Кроме того, в

каждом из экспериментов были использованы все возможные полиномы

вплоть до некоторой определенной степени. Другими словами, мы

сначала выбрали степень С, а затем — все значения и и v, удовлетворяю-

щие условиям

О < w, - 143 < г < 143 и \v\ + 2и < G. (13.60)

Поскольку вид полинома подбирается с учетом радиуса D окружности, на

которой располагаются источники (а не из размеров реконструированной

области), то не удивительно, что для точного восстановления требуются

большие значения G.

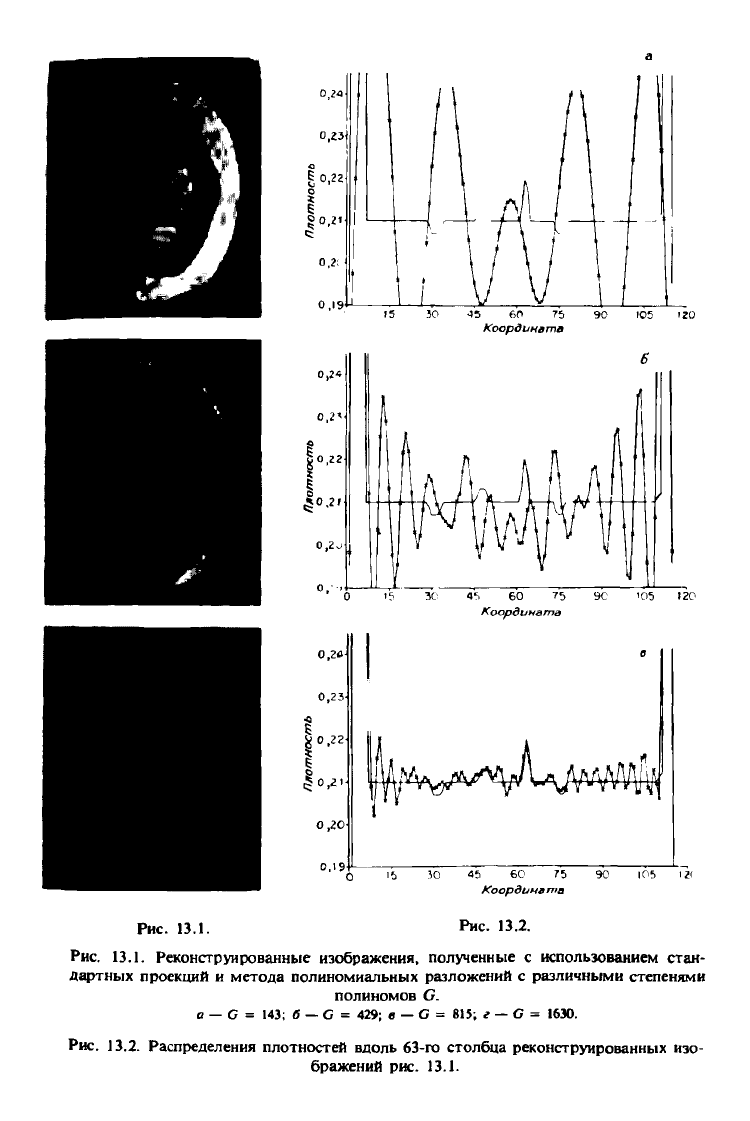
На рис. 13.1 приведены четыре изображения, реконструированные мето-

дом полиномиальных разложений, причем, согласно формуле (13.60), вели-

чина С выбрана равной 143, 429, 815 и 1630 соответственно. Отметим, что

последнее из упомянутых значений оказывается слишком большим, исходя

из развитой в данной главе теории, однако то, что его взяли, может быть

оправданно стремлением к более точному выполнению условия ортого-

нальности функций, чем это предусматривается соотношением (13.29). Рас-

пределения восстановленных значений, взятых вдоль 63-го столбца, приве-

дены на рис. 13.2, а меры различий между изображениями — в табя. 13.1.

Заметим, что появляющиеся при аппроксимации более высоких порядков

необычные артефакты стали заметны из-за выбранных нами уровней бело-

го и черного. В целом реконструкция изображения производится достаточ-

но точно, что следует из величины мер различия между изображениями.

Таблица 13.1

Меры различия между изображениями для реконструкций на рис. 13.1

Степень

d г е t

полинома

143 0,5564 0,3545 0,2374 542

429 0,2413 0,1315 0,1415 725

815 0,1772 0,0769 0,1020 953

1630 0,1586 0,0650 0,0926 1452

0,20

45 60 7Ь 90 105 »20

Координата

1*> 30 45 60 75 90 105 i К

Координата

Рис. 13.1.

Рис. 13.2.

Рис. 13.1. Реконструированные изображения» полученные с использованием стан-

дартных проекций и метода полиномиальных разложений с различными степенями

полиномов С.

a — G= 143; б

—

G = 429; в — С = 815; г — С = 1630.

Рис. 13.2. Распределения плотностей вдоль 63-го столбца реконструированных изо-

бражений рис. 13.1.

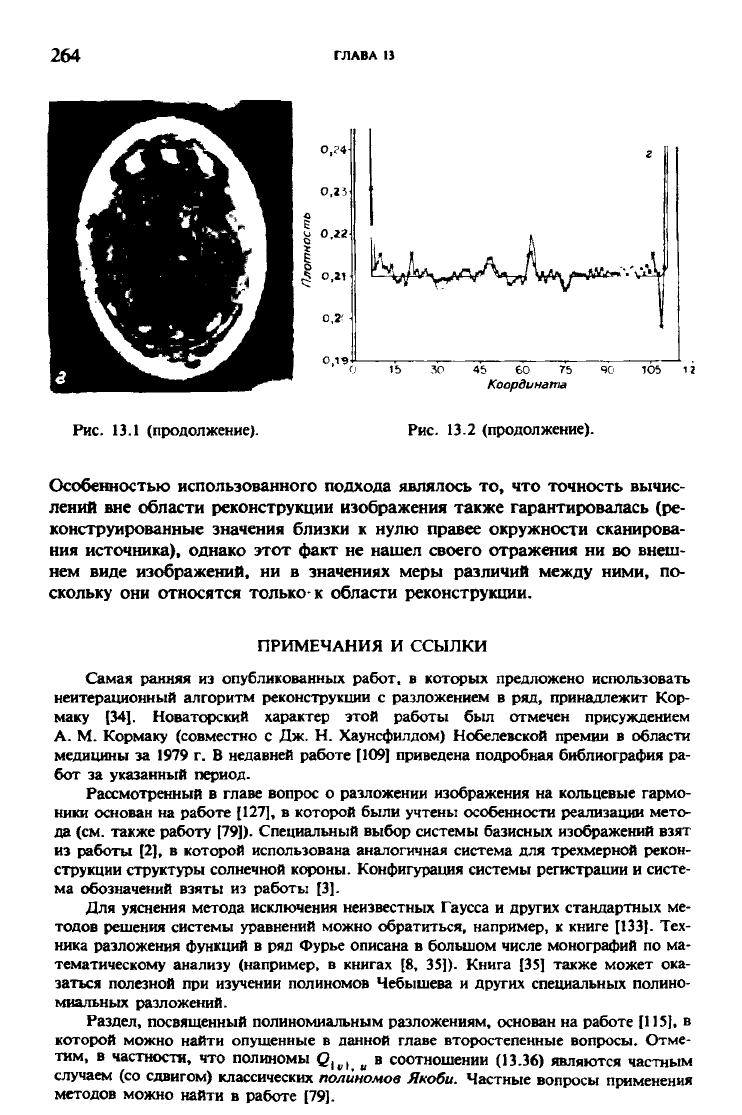
264

ГЛАВА 13

Рис. 13.1 (продолжение). Рис. 13.2 (продолжение).

Особенностью использованного подхода являлось то, что точность вычис-

лений вне области реконструкции изображения также гарантировалась (ре-

конструированные значения близки к нулю правее окружности сканирова-

ния источника), однако этот факт не нашел своего отражения ни во внеш-

нем виде изображений, ни в значениях меры различий между ними, по-

скольку они относятся только-к области реконструкции.

ПРИМЕЧАНИЯ И ССЫЛКИ

Самая ранняя из опубликованных работ, в которых предложено использовать

неитерационный алгоритм реконструкции с разложением в ряд, принадлежит Кор-

маку [34]. Новаторский характер этой работы был отмечен присуждением

А. М. Кормаку (совместно с Дж. Н. Хаунсфилдом) Нобелевской премии в области

медицины за 1979 г. В недавней работе [109] приведена подробная библиография ра-

бот за указанный период.

Рассмотренный в главе вопрос о разложении изображения на кольцевые гармо-

ники основан на работе

[127],

в которой были учтены особенности реализации мето-

да (см. также работу [79]). Специальный выбор системы базисных изображений взят

из работы [2], в которой использована аналогичная система для трехмерной рекон-

струкции структуры солнечной короны. Конфигурация системы регистрации и систе-

ма обозначений взяты из работы [3].

Для уяснения метода исключения неизвестных Гаусса и других стандартных ме-

тодов решения системы уравнений можно обратиться, например, к книге

[133].

Тех-

ника разложения функций в ряд Фурье описана в большом числе монографий по ма-

тематическому анализу (например, в книгах [8, 35]). Книга [35] также может ока-

заться полезной при изучении полиномов Чебышева и других специальных полино-

миальных разложений.

Раздел, посвященный полиномиальным разложениям, основан на работе

[115],

которой можно найти опущенные в данной главе второстепенные вопросы. Отме-

тим,

в частности, что полиномы (?,„,

в соотношении (13.36) являются частным

случаем (со сдвигом) классических

полиномов

Якоби.

Частные вопросы применения

методов можно найти в работе [79].

Реконструкция изображения

трехмерного объекта

Если требуется реконструировать трехмерный объект, используя при

этом алгоритмы, рассмотренные в предыдущих разделах, то нам представ-

ляется единственная возможность — получить отдельные сечения объекта,

а затем синтезировать по ним трехмерное распределение. Подобный спо-

соб реконструкции может породить целый ряд проблем, основная из кото-

рых связана с большими затратами машинного времени. В течение време-

ни,

необходимого для регистрации полного объема данных, пациент может

шевелиться, что будет приводить к рассогласованию сечений. Более того,

для движущихся органов, таких, как легкие и в особенности сердце, посто-

янные смещения являются неизбежными, поэтому в принципе необходимо

регистрировать исходные данные по всем сечениям одновременно.

В ряде случаев эволюция объекта во времени содержит в себе полезную

информацию. Если требуется следить за движением стенки сердца или за

распространением радиоактивных контрастирующих веществ в системе кро-

вообг цения, то возникает важная задача реконструкции полного трехмер-

ного объекта за достаточно короткий отрезок времени. Таким образом,

при этом можно говорить о четырехмерной (пространственно-временнбй)

реконструкции изображения.

Из всех схем сканирования, рассмотренных в разд. 3.4, лишь пятая схе-

ма (рис. 3.3,с)) пригодна для получения подобной информации. В данной

главе будут рассмотрены алгоритмы реконструкции изображения по дан-

ным,

зарегистрированным именно в данной схеме.

14.1.

РАЗЛОЖЕНИЯ ФУНКЦИИ

В РЯД ПО ТРЕХМЕРНОМУ БАЗИСУ

Для описания трехмерных объектов воспользуемся цилиндрической си-

стемой координат, или, другими словами, будем характеризовать каждую

точку объекта набором трех чисел (г, ф

zY При этом предполагается, что

имеется ось z (т.е. бесконечно протяженная прямая линия), вдоль которой

отсчитывается координата z. Множество точек с координатами (г, ф, г

где z

фиксировано, а координаты (г, ф) меняются, образует плоскость,

перпендикулярную оси z и пересекающую ее в точке z

. Особо выделим ко-

ординаты (г, ф)

считая их полярными координатами на плоскости с нача-

лом координат в точке ее пересечения с осью г.

266

ГЛАВА 14

Заметим, что указанная система координат представляется наиболее

естественной, рассматривая трехмерный объект в виде набора поперечных

сечений, причем каждое из них является плоскостью с фиксированным зна-

чением Z, а значения трехмерной функции объекта, ограниченные данной

плоскостью, являются функцией двух полярных координат (г, 0).

Будем предполагать, что все подлежащие реконструкции объекты име-

ют конечные размеры. Говоря более строго, при этом предполагается, что

существуют такие постоянные величины Е и F

для которых

ф, z) = 0 при |г| > Е или М > F, (14.1)

где

функция

/(г, ф, z) Задает значения реконструируемого объекта в точках

с координатами (г, ф, г).

В настоящей книге рассматриваются лишь те алгоритмы реконструкции

истинно трехмерных объектов, которые связаны с методом разложения

функций в ряд. Как и в случае двумерной реконструкции, мы будем предпо-

лагать наличие фиксированного множества из J

элементарных

объектов

(б,,

. . ., bj), линейная комбинация которых дает приемлемое приближе-

ние к любому реальному объекту, описываемому функцией /, и изображе-

ние которого необходимо реконструировать.

В качестве примера подобного подхода, который соответствует технике

дискретизации напх л элементов, рассмотрим следующую модель. Пусть

с — положительное вещественное число, a W

—

целое число, причем

(W + ±)с >

акс {£, F}. (14.2)

Куб,

центр которого совпадает с началом цилиндрической системы ко-

ординат (0, 0, 0) и который имеет четыре грани, параллельные оси г, с раз-

мерами сторон (2W + 1)с, ограничивает область пространства, внутри ко-

торой функция/ отлична от нуля. Мы делим данный куб на (2W + 1) х

х (2W+ 1)х (2И^+ 1) меньших кубов размером с х с х с каждый, ко-

торые называем элементами объема (или сокращенно злобами, разд. 2.4).

Пусть

J = (2W + I)

. (14.3)

Пронумеруем элементы объема числами от 1 до

и введем функцию вида

(

—

для значений координат (г, ф, z)

принадлежащих У-му элементу объема; (14.4)

0 — для остальных координат.

Используемая нами аппроксимация/функции/объекта определяется выра-

жением

JV, <£,*)= 5>A(r,0,zX (14.5)

РЕКОНСТРУКЦИЯ ИЗОБРАЖЕНИЯ ТРЕХМЕРНОГО ОБЪЕКТА 267

гдех— среднее поу-му элементу объема значение функции/.

Имеется и другой способ выбора базисных объектов, основанный на

разложении изображения на кольцевые гармонические составляющие (разд.

13.1).

Суть метода состоит в следующем. Пусть end — положительные

вещественные, a U, К, W

—

положительные целые числа, такие, что

(W + $)с > F и Ш > Е. (14.6)

Пусть также

J = U(2V + 1)(2W + 1). (14.7)

При 1 < j' < J существует единственное значение и в интервале

< и ^ U

—

1, единственное значение v в интервале

—

V ^ v < К, а так-

же единственное значение w в интервале

—

W < w <

для которых спра-

ведливо соотношение

j = и + (w + v(2W + 1))L/ + (W + F(2W + 1))L/ + 1. (14.8Г

Значения и, v и w

удовлетворяющие соотношению (14.8), будут обозна-

чены

и>

соответственно, однако в тех случаях, когда это не вызыва-

ет путаницы, индексы будут опускаться.

Определим при

< у < J базисный объект

Ь.

с помощью выражения ви-

да

Ъ,(г,

ф, z) = RJLr)TM>SJLz\ (14.9)

где/?

и T

определяют, исходя из выражений (13.12) и (13.13), а

I при \z - wc\ < с/2,

Т при \z - wc\ = с/2, (14.10)

0 для остальных с.

Заметим, что последнее определение для случая \z

—

wcl = с/2 является

математическим формализмом, не играющим никакой роли при дальней-

шем рассмотрении.

Каждый из рассматриваемых базисных объектов, описываемых соотно-

шением (14.9), равен нулю вне параллелепипеда высотой с, а внутри его он

аналогичен величине базисного изображения, понятие о котором использо-

вано нами при разложении картины на кольцевые гармоники. Поскольку

интересующие нас характеристики объекта, к сожалению, существенно ме-

няются с изменением z на величину с или меньше, то приведенные в разд.

13.1 аргументы в пользу возможностей аппроксимации изображения разло-

жением по кольцевым гармоникам можно распространить на случай ап-

проксимации объекта линейной комбинацией функций, определенных соот-

ношением (14.9).