Хермен Г. Восстановление изображений по проекциям: Основы реконструктивной томографии

Подождите немного. Документ загружается.

238

ГЛАВА 12

Давая математически точную постановку задачи, будем считать, что

для любого

в интервале 1 < у < / величина Ej обозначает множество но-

меров элементов изображения, имеющих общую сторону с у-м элементом

изображения, и пусть К обозначает множество номеров элементов изобра-

жения, имеющих только одну общую вершину с у-м элементом изображе-

ния при (л х л)-разбиении изображения. Если обозначить через х вектор

изображения перед сглаживанием, а через х' тот же вектор после сглажи-

вания, то получим

х' = Sx, (12.34)

где S — матрица размерностью / х У, (/, Аг)-й элементSj

которой опреде-

ляется следующим образом:

при

/с

= у,

при к е Ej,

при

keV

О для остальных к,

(12.35)

Подобным образом определенная матрица S называется базисной сглажи-

вающей матрицей, связанной с системой сглаживающих весовых коэффи-

циентов (w,

, w

). Отметим, что базисная сглаживающая матрица сим-

метрична.

Частным случаем, который приводит нас к понятию базисной сглажи-

вающей матрицы, является байесовский критерий оптимальности, пред-

ставленный в форме (6.33). При этом V

— ковариационная матрица, свя-

занная с априорным распределением вероятности р

[соотношение

(6.31)].

Если выборки X представляют собой векторы изображения, разумно пред-

положить, что компоненты х и х

не коррелируют между собой, если со-

ответствующие элементы изображения не имеют по крайней мере общих

сторон или вершин, а также что ковариация х и х

определяются тем, име-

ют ли упомянутые элементы изображения общие стороны или вершины.

При этом становится ясно, что У

— базисная сглаживающая матрица.

Другим связанным с введенным выше понятием сглаживающей матри-

цы,

также используемым при реконструкции изображения, является поня-

тие модифицированной сглаживающей матрицы, к определению которой

мы переходим.

Пусть N — множество номеров элементов изображения, не лежащих на

краю изображения, дискретизированного на п х п элементов изображения.

Пусть также Z будет диагональной матрицей из J х J элементов, (/, у)-й

элемент которой определяется как

'V/ = [!

npH/6/V

- (12.36)

(<) для остальных

у"

АЛГОРИТМЫ РЕКОНСТРУКЦИИ С КВАДРАТИЧНОЙ ОПТИМИЗАЦИЕЙ 239

Очевидно, что если х — вектор изображения, то Zx — также вектор изо-

бражения, характеризующий, как и

дискретизированное изображение, за

исключением того, что плотности элементов изображения на его краю рав-

ны нулю. Матрица S' называется

модифицированной сглаживающей

мат-

рицей, связанной с

системой

весовых

коэффициентов

, w

если

справедливо равенство

S' = SZS, (12.37)

где 5 — базисная сглаживающая матрица, связанная с той же системой ве-

совых коэффициентов w

, w

Рассмотрим пример использования модифицированной сглаживающей

матрицы для целей реконструкции изображений. Предположим, что требу-

ется получить решение задачи о дискретной реконструкции изображения, в

котором значения дг

, относящиеся к соседним элементам изображения, в

среднем близки друг другу. Математически данное условие сводится к

требованию, чтобы величина суммы вида

(12.38)

была бы наименьшей из возможных, где

Nj =

EjVV

(12.39)

при 1 ^ у < /, т.е. Nj — множество номеров элементов изображения, гра-

ничащих с 7-м элементом изображения.

Пусть S — базисная сглаживающая матрица, связанная с системой весо-

вых коэффициентов вида 1, -1/8, —1/8, и пусть также

означает транс-

позицию у-й строки матрицы S. Нетрудно проверить, что

- I I **) =

(*7*)

Sjs]x. (12.40)

Таким образом,

if*/- о I

к) =

ВА\

(12-41)

где

В=

Zsjs].

(12.42)

je/v

До сих пор мы стремились показать, что процедура минимизации сум-

мы (12.38) фактически сводится к минимизации квадратичной формы х'Вх.

Очевидно, что матрица В симметрична и, учитывая соотношение (12.41),

240

ГЛАВА 12

неотрицательно определенная. Теперь покажем, что В является также и

модифицированной сглаживающей матрицей.

Определим матрицу Т с помощью соотношения вида

Т = SZ, (12.43)

где S — базисная сглаживающая матрица, связанная с системой весовых

коэффициентов вида (— 1, —1/8, —1/8), a Z — диагональная матрица,

определенная выражением (12.36). При этом (/, *)-й элемент матрицы Т

имеет вид

, <-*. при*

(1244)

для остальных к.

Следовательно, (/, у)-й элемент матрицы SZC равен

(SZSXj = (SZS)

jti

= X

h.kSk.i

= I

ЧкЬ.*

= I

sl)

ijy

*=1 keN keS

(12.45)

где B

j есть (i, у)-й элемент матрицы В. Последнее доказывает, что ма-

трица

В = SZS (12.46)

является модифицированной сглаживающей матрицей, связанной с систе-

мой весовых коэффициентов вида 1, —1/8, —1/8.

В общем случае перемножение У-мерного вектора х с матрицей S из

J х J элементов требует J

операций скалярного умножения. Однако если

в качестве указанного вектора взят вектор изображения, связанный с его

дискретизацией на п х п элементов изображения (J = л

), а в качестве ма-

трицы — сглаживающая матрица, то число потребных для вычисления

значений Sx операций скалярного умножения приблизительно равно kJ, где

к = 3 для базисной сглаживающей матрицы и к = 6 для модифицирован-

ной сглаживающей матрицы, в чем легко убедиться из рассмотрения про-

цедуры сглаживания, описываемой соотношением (11.45).

В наших задачах, где обычно число J > 10000, требования к объему вы-

числений Sx существенно различаются в зависимости от того, является ли

5 матрицей общего вида или же сглаживающей матрицей. Анализируя при-

веденную в разд. 12.1 таблицу, можно уяснить целесообразность введения

предположения о том, что обе матрицы В и С, фигурирующие в соотноше-

нии (12.5), являются сглаживающими.

АЛГОРИТМЫ РЕКОНСТРУКЦИИ С КВАДРАТИЧНОЙ ОПТИМИЗАЦИЕЙ 241

12.4.

ПРИМЕНЕНИЕ МЕТОДА РИЧАРДСОНА

ДЛЯ РЕКОНСТРУКЦИИ ИЗОБРАЖЕНИЙ

Процедура итерации алгоритма Ричардсона в приложении к проблеме

реконструкции изображения описывается выражениями (12.24) и (12.28). В

обоих случаях на каждом шаге итерации необходимо вычислять величину

A(y -

{k)

(12.47)

На первый взгляд может показаться, что указанные вычисления вызовут

большие трудности, однако, как будет показано ниже, при некоторых при-

нятых предположениях трудоемкость вычислений по формуле (12.47) вовсе

не пропорциональна размерам взятых матриц.

Предположим, что матрица А диагональная. Разумность данного пред-

положения для наших задач подтверждается тем, что в табл. 12.1 имеется

лишь единственный случай, когда матрица А недиагональна (при байесовс-

кой оценке, для которой А = V

). Однако V

является ковариационной

матрицей случайной функции, выборки которой при измерениях представ-

ляют собой векторы ошибок измерений. Предположение о диагональности

матрицы А (а следовательно, и матрицы V

) эквивалентно гипотезе о том,

что погрешности при экспериментальном определении величины <r

, х) (где

rj — /-я строка матрицы проекций R) друг с другом не коррелируют. Ре-

альные и модельные эксперименты подтверждают разумность сделанного

предположения.

Если матрица А диагональна и имеет диагональные элементы a

,, то

A(y - K.v'*') - £ а

{у> ~ W х«

»г

(

. (12.48)

Выражение в правой части (12.48) можно вычислить за / шагов путем до-

бавления на каждом шаге к текущему значению нового слагаемого. Вычис-

лительная процедура на каждом шаге весьма сходна с одиночной итерацией

в алгебраических алгоритмах реконструкции (разд. 11.1). На любой стадии

вычислений требуются значения лишь одной строки матрицы R, более то-

го,

лишь ее ненулевые значения. Единственное существенное различие меж-

ду рассматриваемой процедурой (12.48) и /-ступенчатым алгебраическим

алгоритмом реконструкции состоит в том, что если в алгебраических алго-

ритмах вектор изображения обновляется на каждой стадии (и, следователь-

но,

необходимо запоминать лишь один У-мерный вектор), то при вычисле-

нии по формуле (12.48) необходимо хранить в памяти два значения J-

мерного вектора: вектор х^

к)

и сумму, которую мы вычисляем.

Если предположить, что D — сглаживающая матрица (на практике D

обычно выбирают диагональной; разд. 6.4), то все остальные операции в

(12.24) и (12.28) являются операциями умножения 7-мерного вектора на

сглаживающую матрицу, или на скаляр, либо сложения двух У-мерных век-

торов. Все упомянутые операции с точки зрения вычислений, возможно,

242

ГЛАВА 12

даже менее трудоемки, чем расчет по формуле (12.48). Таким образом, об-

щий объем вычислений для одной итерации в методе Ричардсона имеет

тот же порядок, что и для / итераций в алгебраических алгоритмах рекон-

струкции. Поскольку в рассмотренном выше методе SIRT на одном шаге

итерации принимают во внимание все / измеренных значения (в то время

как в алгебраических алгоритмах реконструкции используется лишь одно),

то только что полученный вывод является очевидным. Единственный недо-

статок метода Ричардсона — необходимость запоминания дополнительных

данных.

Поскольку метод Ричардсона является итерационным, то применение

искусственных приемов, аналогичных изложенным в разд. 11.4, приведет

лишь к незначительным изменениям алгоритма.

12.5.

ПРАКТИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ

МЕТОДА РИЧАРДСОНА

Применимость метода Ричардсона будет продемонстрирована на при-

мере двух изображений, реконструированных по стандартным проекциям.

Для первой реконструкции были выбраны следующие величины входя-

щих в формулу (12.3) параметров: х

— выходные данные, полученные в

результате применения дискретного обратного проецирования в сочетании

с процедурой мультипликативной нормировки (рис. 7.5,6). W

эквивалент-

но U

a W

— сумме (В + £/

), где В — модифицированная сглаживающая

матрица, связанная с системой весовых коэффициентов вида 1, —1/8,-1/8

(разд.

12.3). Значение дг

(0)

выбирается равным х

, что вытекает из соотно-

шения (12.22), когда w

(0)

— нулевой вектор. Вычисление по формуле (12.24)

производится за четыре итерации, причем параметр \^ = X выбирается

согласно соотношению (12.32). После каждой итерации производят опера-

ции ограничения и нормирования. Полученные результаты приведены на

рис. 12.1 и 12.2, а также в табл. 12.2.

Наиболее важный вывод, полученный при реконструкции изображений,

состоит в том, что в процессе итераций никогда не достигается предельное

значение плотности в изображении. Например, значение llz

—

Ри^

для

к = 1, 2, 3 и 4 равны соответственно 1316, 848, 594 и 442. Поскольку пред-

полагается, что алгоритм дает сходимость к решению системы уравнений

Ри - z [где матрицы Р, и и z определены выражениями (12.10), (12.7) и

(12.11) соответственно], то, вероятно, потребуется гораздо большее число

итераций, прежде чем можно будет считать значение х^

к)

хорошей аппрок-

симацией искомого путем минимизации вектора. Последнее является об-

щей проблемой в методах квадратичной оптимизации, скорости сходимо-

сти в которых достаточно низки, и требуется большое число итераций для

получения реконструированного изображения приемлемого качества. Дан-

ный итерационный процесс может быть весьма трудоемким и на использу-

емой в эксперименте ЭВМ требовал около 5 мин машинного времени на

каждую итерацию.

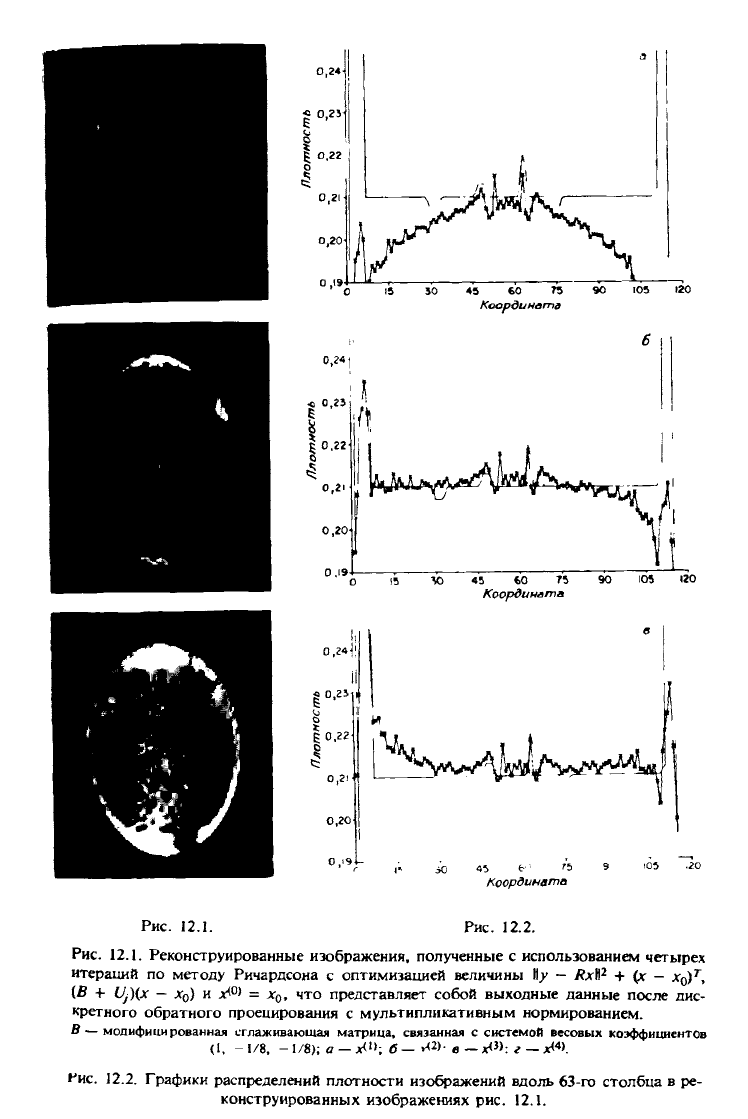
Рис. 12.1.

0,24

< 0,23

| 0,22

0,2i

«Э 60 75 90

Координата

llll

0,24f

0,22

0,2.

^vИУ/^vvУ^4J

45 Ь^ 7$

Координата

Рис. 12.2.

Рис. 12.1. Реконструированные изображения, полученные с использованием четырех

итераций по методу Ричардсона с оптимизацией величины

- Rx№ + {х - дг

)

{В + (Jj)(x - х

) и х<°> = дг

, что представляет собой выходные данные после дис-

кретного обратного проецирования с мультипликативным нормированием.

— модифици рованная

сглаживающая матрица, связанная с системой весовых коэффициентов

(1,

-1/8, -1/8); a-*

h б— Л

>- е-х<

>: г - х<

Ь'ис. 12.2. Графики распределений плотности изображений вдоль 63-го столбца в ре-

конструированных изображениях рис. 12.1.

244

ГЛАВА 12

J/V^

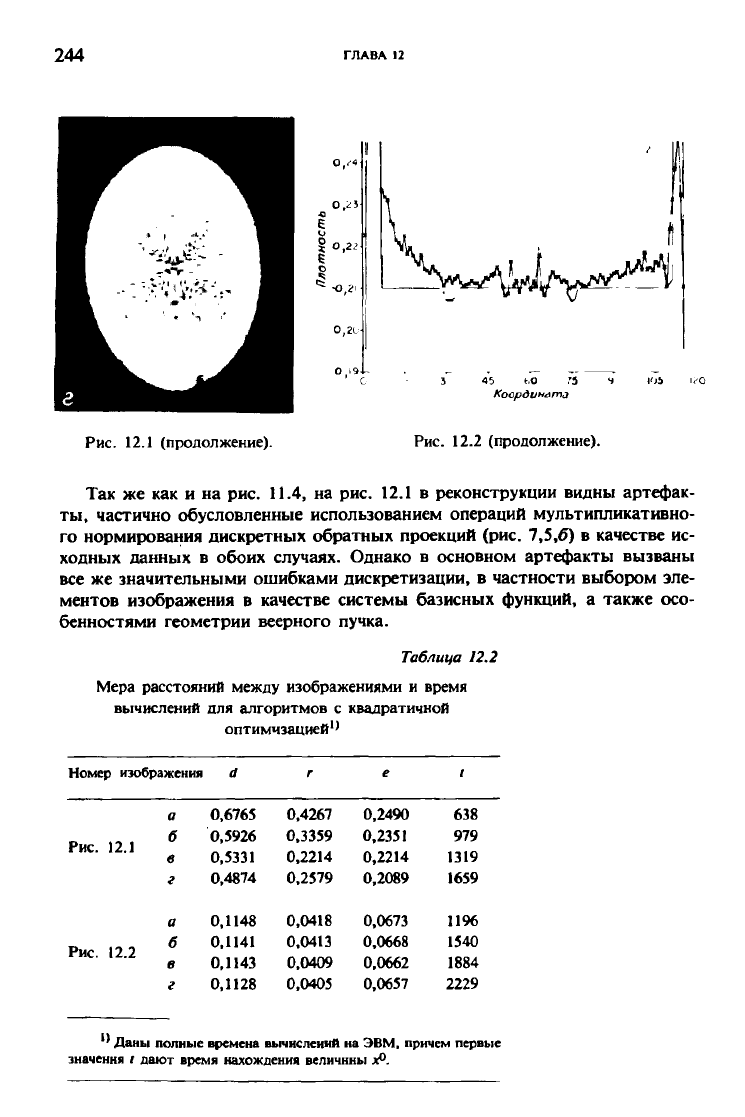
Рис. 12.1 (продолжение).

Координата

Рис. 12.2 (продолжение).

Так же как и на рис. 11.4, на рис. 12.1 в реконструкции видны артефак-

ты,

частично обусловленные использованием операций мультипликативно-

го нормирования дискретных обратных проекций (рис. 7,5,6) в качестве ис-

ходных данных в обоих случаях. Однако в основном артефакты вызваны

все же значительными ошибками дискретизации, в частности выбором эле-

ментов изображения в качестве системы базисных функций, а также осо-

бенностями геометрии веерного пучка.

Таблица

12.2

Мера расстояний между изображениями и время

вычислений для алгоритмов с квадратичной

оптимизацией

Номер

изображения

€

0,6765

0,4267

0,2490

638

Рис.

12.1

0,5926 0,3359 0,2351

979

Рис.

12.1

0,5331

0,2214 0,2214

1319

0,4874

0,2579 0,2089

1659

0,1148

0,0418

0,0673

1196

Рис.

12.2

0,1141

0,0413 0,0668

1540

Рис.

12.2

0,1143

0,0409

0,0662

1884

0,1128

0,0405

0,0657

2229

' Даны полные времена вычислений на ЭВМ, причем первые

значения t дают время нахождения величины х°.

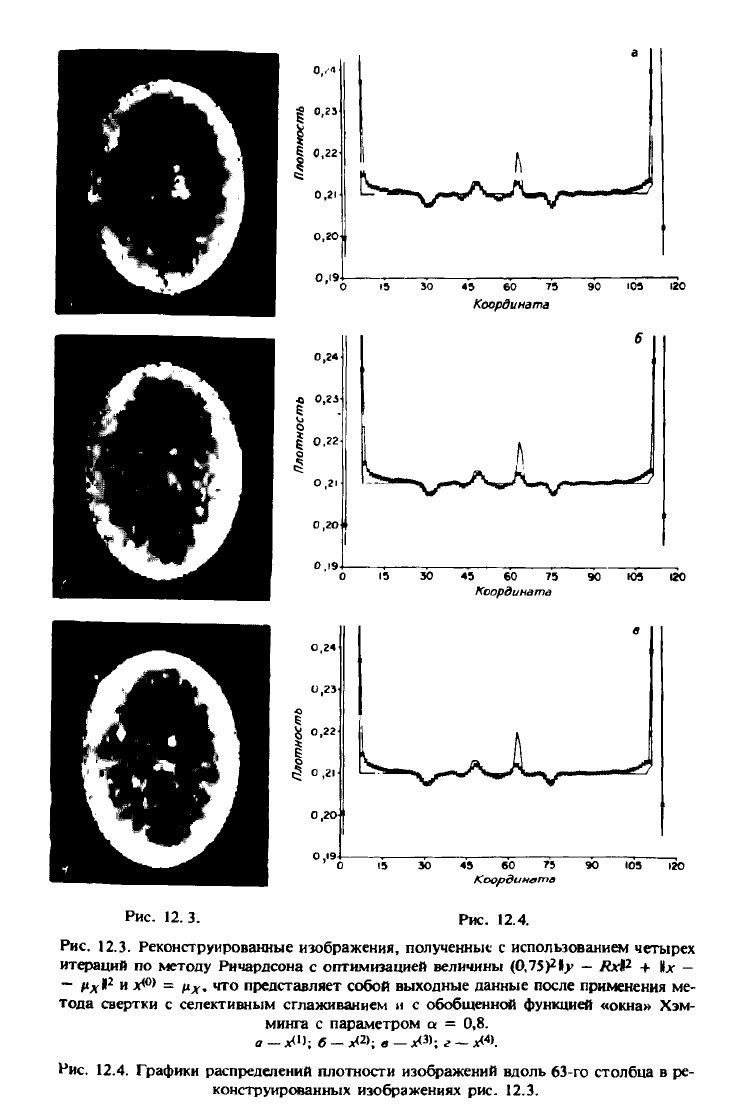
Рис. 12.3.

Рис. 12.4.

Рис. 12.3. Реконструированные изображения, полученные с использованием четырех

итераций по методу Ричардсона с оптимизацией величины (OJSply — /ЫР + Их -

— Мл И

и л<°> = ц

. что представляет собой выходные данные после применения ме-

тода свертки с селективным сглаживанием и с обобщенной функцией «окна» Хэм-

минга с параметром а — 0,8.

О _

Л<1);

_ д<2)

; в

_ j<3).

_ j<4).

Рис. 12.4. Графики распределений плотности изображений вдоль 63-го столбца в ре-

конструированных изображениях рис. 12.3.

АЛГОРИТМЫ РЕКОНСТРУКЦИИ С КВАДРАТИЧНОЙ ОПТИМИЗАЦИЕЙ 246

^5 30 45 60 75 90 105

Координата

Рис. 12.3 (продолжение). Рис. 12.4 (продолжение).

Для второй реконструкции параметры были подобраны таким образом,

чтобы найденное потом значение вектора являлось байесовской оценкой х,

которая минимизировала бы функцию (12.3) при W =

^//,

= Uj и

= ц

, делала бы функцию к(х) тождественной с функциями в соотноше-

ниях (12.3) и (11.26). Действительно, значения \L

и г брались те же, что и в

разд.

11.5, и представляли собой селективно сглаженные выходные данные

полученные по сверточным алгоритмам с использованием функции об-

общенного «окна» Хэмминга с а = 0,8 (рис. 10.5), а г = 0,75. Процедуры

селективного сглаживания, ограничения и нормирования брались точно с

теми же значениями параметров, что и в разд. 11.5. Соответствующие им

реконструированные изображения приведены на рис. 12.3 и 12.4, которые

целесообразно было бы сравнить с рис. 11.8 и 11.9, реконструированными

с использованием алгебраических алгоритмов реконструкции и с целью оп-

тимизации той же функции при помощи тех же искусственных приемов. За-

метим, что /-итерации в алгебраическом алгоритме реконструкции соот-

ветствуют одной итерации в методе Ричардсона в том смысле, что все лу-

чевые суммы в обоих случаях используются лишь один раз. Вновь следует

отметить довольно низкую скорость сходимости при использовании мето-

да квадратичной оптимизации, которая становится еще более очевидной из

сравнения соответствующих данных табл. 12.2 и 11.1.

Заключительные замечания в конце разд. 11.5 о сравнительной эффек-

тивности применения алгебраических алгоритмов реконструкции и сверточ-

ного алгоритма почти дословно можно повторить, что и при сравнении ме-

тода квадратичной оптимизации и сверточного алгоритма. Что же касает-

ся сравнения алгебраических алгоритмов реконструкции с рассмотренным в

данной главе методом, то, как было установлено, алгебраические алгорит-

мы реконструкции требуют гораздо меньший объем памяти и дают боль-

НЕИТЕРАЦИОННЫЕ АЛГОРИТМЫ РЕКОНСТРУКЦИИ 247

ший объем данных за один цикл вычислений. С другой стороны, в рамках

метода квадратичной оптимизации возможности выбора квадратичного

функционала шире, нежели в алгебраических алгоритмах реконструкции, и,

кроме того, итерации по методу Ричардсона требуют несколько меньше

машинного времени, чем в алгебраических алгоритмах реконструкции, хо-

тя,

возможно, это и не дает слишком больших выгод.

ПРИМЕЧАНИЯ И ССЫЛКИ

Причины, по которым рассмотренные в данной главе методы получили назва-

ние «алгоритмы реконструкции с одновременными итерациями» состоят в том, что

одноименный метод SIRT был впервые использован в [47] для реконструкции изо-

бражений.

Из последних результатов по применению метода SIRT следует назвать работу

[101].

Определения и основные положения линейной алгебры, которые мы здесь ис-

пользовали, можно найти в книге [37]. Наш вывод для матриц Риг требуемого ви-

да основан на работе [72], которая может быть полезной для заполнения отдельных

пробелов в приведенном анализе. Последнее развитие указанной работы дано в [10]

и содержит анализ соотношения (12.33) и сглаживающих матриц, а также двух нери-

чардсоновских методов решения системы уравнений Ри = г, а именно метода со-

пряженного градиента

и метода

полуитераций

Чебышева.

Термин «метод Ричард-

сона» в обобщенном смысле, как он здесь употреблялся, использован, например, в

работе

[159],

в которой приводится также библиография работ по математическим

основам метода и вывод соотношения (12.33).

Дополнительные сведения по методам квадратичной оптимизации и SIRT мож-

но получить по уже цитированным выше работам, а также по библиографии к ним.