Хермен Г. Восстановление изображений по проекциям: Основы реконструктивной томографии

Подождите немного. Документ загружается.

218

ГЛАВА 11

Справедливость этого утверждения непосредственно вытекает из сходи-

мости релаксационного метода решения системы неравенств, поскольку

множество векторов М, для которых выполняется условие (11.47), можно

охарактеризовать следующим образом. Пусть при 1 ^ j ^ J имеем

_! - {х|*;</<} (Ц.51)

j= {x\-Xj£ -А}. (11.52)

Тогда

М = f)Mj. (11.53)

i= 1

Таким образом, множество А/ векторов, удовлетворяющих условию

(11.47),

можно проанализировать точно так же, как и множество N в

разд. 11.2. Читатель легко может убедиться в том, что применение релак-

сационного метода для решения системы неравенств при замене множества

N на А/, при выборе релаксационного параметра равным единице и началь-

ного вектора J? позволяет получить вектор т

(J?) за U итераций, где т

определено соотношением (11.48). Таким образом, процедура ограничения

в данном случае эквивалентна применению релаксационного метода к си-

стеме с большим числом неравенств. Этот вывод завершает рассмотрение

вопроса о сходимости процедуры (11.50).

Существуют и другие разновидности процедуры ограничения, помимо

описываемых соотношениями (11.48) и (11.49). Например, имеется способ

определения таких ограничивающих функций

которые в сочетании с ал-

горитмом (11.41) обеспечивают сходимость к решению с минимальной нор-

мой (11.40) и (11.47). Другой метод полезен в случае, когда заранее извест-

но о наличии в изображении лишь двух различных уровней плотности (что

имеет место в некоторых задачах неразрушающего контроля), и состоит в

использовании функции т

, которая устанавливает величины J? равными

либо одному, либо другому значению плотности.

Еще один искусственный прием, с которым мы уже познакомились в

книге, — это операция нормировки, которая рассматривалась в разд. 7.2 в

связи с алгоритмом обратного проецирования. Иногда оказывается, что

многократное нормирование в процессе итераций ведет к повышению ско-

рости сходимости к ожидаемой оценке в алгебраическом алгоритме рекон-

струкции.

Несмотря на то что существуют и другие приемы, об использовании ко-

торых указано в литературе, данный раздел будет завершен рассмотрением

четырех вопросов, связанных с упомянутыми искусственными приемами,

хотя и отличающихся от них деталями.

Существенным параметром, доступным нам для варьирования в ал-

гебраических алгоритмах реконструкции, является релаксационный пара-

АЛГЕБРАИЧЕСКИЕ АЛГОРИТМЫ РЕКОНСТРУКЦИИ ИЗОБРАЖЕНИЙ 219

метр.

Выше отмечалось, что выбор небольшого значения релаксационного

параметра, как установлено, оказывает положительное влияние на качество

реконструированных изображений при использовании подобных алгорит-

мов (даже с использованием полученных в эксперименте данных), близких

к алгебраическим алгоритмам реконструкции. Оказывается, что малое зна-

чение параметра релаксации (неполная релаксация) обусловливает уменьше-

ние влияния погрешностей в уравнениях и предупреждает появление эффек-

та «соли и перца», часто наблюдаемого на реконструкциях, полученных ал-

гебраическим алгоритмом при больших значениях параметра релаксации.

В отдельных случаях ограниченное использование метода при больших

значениях релаксационного параметра все-таки желательно. Например, при

решении системы неравенств это может существенно сократить вычисле-

ния,

если всякий раз лишь слегка изменять параметр релаксации (=2), что

будет проявляться в зеркальном отображении оценки перед итерацией от-

носительно гиперплоскости, связанной с данным неравенством. Выбороч-

ное применение указанного метода зеркальных отображений может при

определенных условиях гарантировать конечную сходимость.

Выбор начального приближения (оценки) х^ оказывает большое влия-

ние на конечный результат итерационной процедуры, особенно в случаях,

когда вследствие ограниченности по. быстродействию и стоимости средств

число итераций не может быть слишком большим. Например, значение х

(0)

в алгоритме (11.38) принимается равным М

. На практике весьма затруд-

нительно найти среднее значение многомерной случайной функции, описы-

вающей реальное распределение в изображении. Вместо выходных данных,

получаемых при помощи других алгоритмов (таких, как сверточный алго-

ритм или алгоритм обратного проецирования), в алгебраических алгорит-

мах необходимо использовать начальную оценку дг

(0)

. На практике чаще

встречаются случаи построения изображений с однородной градацией ярко-

стей,

возможно, с оце

ненн

ым значением средней плотности изображения

(или даже нулевого уровня) в каждом элизе.

Изменение порядка следования неравенств (или равенств) в системе

может также существенно влиять на реальные характеристики того или

иного алгоритма. В такой системе регистрации исходных данных, как ис-

пользуемая нами стандартная конфигурация, оказывается целесообразным

последовательно брать уравнения, описывающие лучи одного ракурса, а

уже затем переходить к лучам ракурса, при котором направление на источ-

ник образует большой угол (например, в 60

) по сравнению с предыдущим

его положением.

11.5.

ЭФФЕКТИВНОСТЬ АЛГЕБРАИЧЕСКИХ АЛГОРИТМОВ

РЕКОНСТРУКЦИИ

В этом разделе будут продемонстрированы возможности некоторых из

обсуждавшихся выше алгебраических алгоритмов реконструкции примени-

тельно к стандартным проекционным данным.

На всех изображениях представлены картины, полученные после 7-й,

27-й,

37-й и 47-й итераций. На 7-й итерации измерения проводились особо

220

ГЛАВА II

Таблица

111

Мера расстояния между изображениями

и время реконструкции изображений

алгебраическими алгоритмами

Номер

рисунка

0,2397

0,1535

0,1882

919

Рис.

11.2

0,1469

0,1003

0,0799

1542

Рис.

11.2

0,1176

0,0806

0,0385

2162

^г

0,1109

0,0748

0,0414

2786

0,3096

0,1564

0,1666

912

Рис.

11.4

0,2043 0,0970

0,1183

1528

Рис.

11.4

0.1567

0,0723

0,0952

2145

^г

0,1308

0,0605

0,0807

2762

0,3118

0,1512

0,1703

926

Рис.

11.6

0,2039

0,0882

0,1238

1553

Рис.

11.6

0,1540

0,0598

0,0989

2177

0,1257

0,0452

0,0838

2797

0,1068 0,0370

0,0618

1458

Рис.

11.8

0,1000

0,0335

0,0574

2065

Рис.

11.8

0,0947

0,0311 0,0542

2661

^г

0,0904 0,0292

0,0514

3256

тщательно для всех возможных положений источника и детекторов. Для

любого положения источника каждый луч рассматривают последователь-

но,

причем положения источников выбираются так, чтобы два последова-

тельно взятых положения стягивали центральный угол, приблизительно

равный 60° (рис. 5.2).

На рис. 11.2 и 11.3 показаны результаты применения релаксационного

метода решения системы уравнений (11.22) и (11.23) к несовместной систе-

ме уравнений Rx = у при значении параметра релаксации Х

(

** = 1 для всех

к. Последнее аналогично использованию алгоритмов (11.1) и (11.2). Необ-

ходимо выбрать х^ равным результатам, полученным после применения

алгоритма дискретного обратного проецирования с мультипликативной

нормировкой (рис. 7.5,в). Качество полученных изображений совершенно

неприемлемо, и оно существенно не улучшается при последующих итераци-

ях.

В табл. 11.1 приведены данные о мерах расстояний между изображени-

ями и о времени его получения.

Метод неполной релаксации существенно повышает качество изображе-

ний.

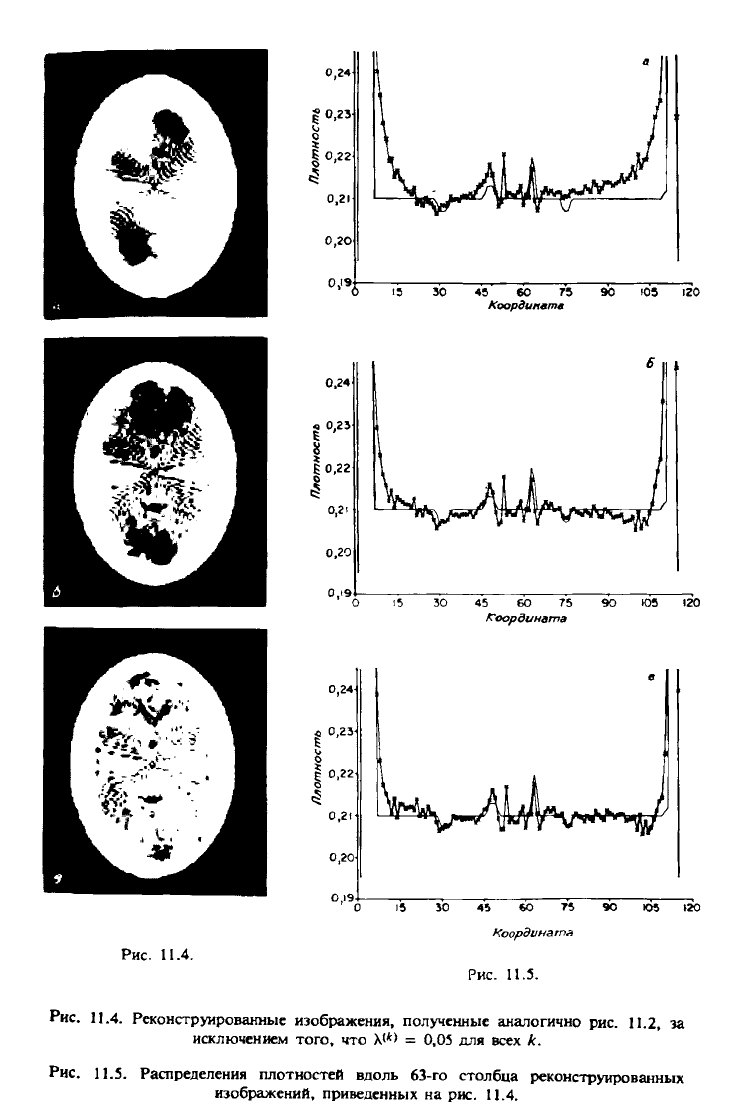
На рис. 11.4 и 11.5 представлены результаты машинных эксперимен-

тов,

аналогичных во многих отношениях тем, в результате которых были

получены рис. 11.2 и 11.3, однако при Х

(А:)

= 0,05 для всех к. Из рисунков

видно существенное повышение качества изображений благодаря простому

изменению параметра релаксации.

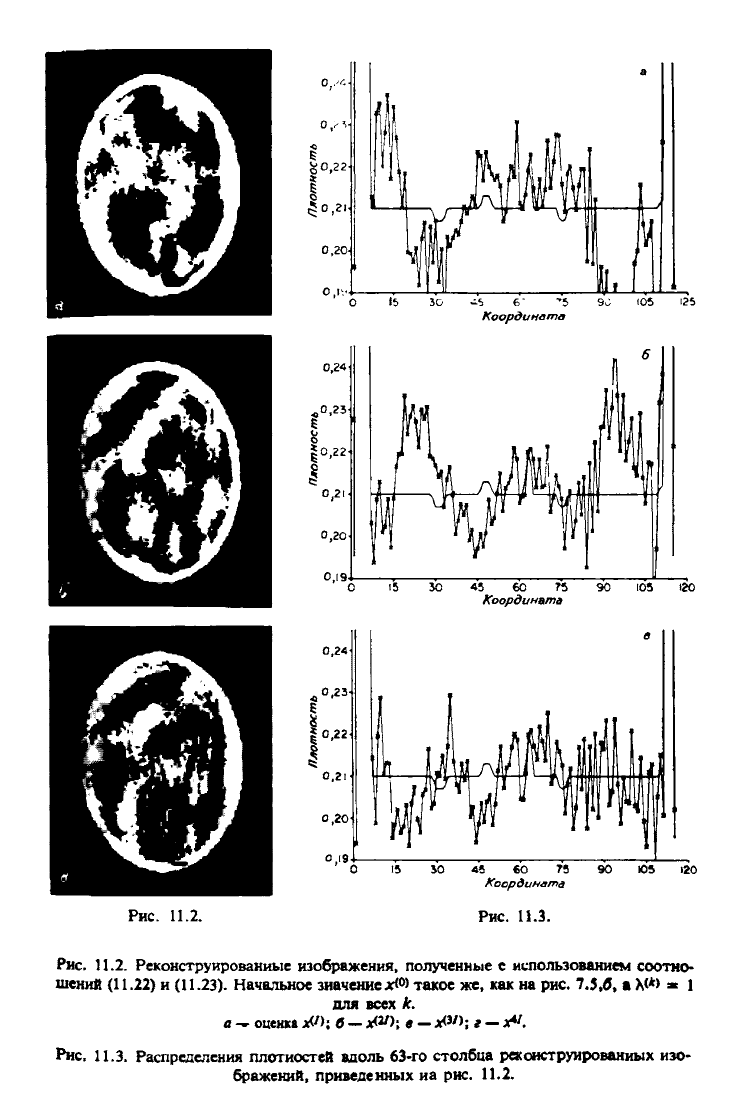
Рис. 11.2.

Рис. 11.3.

Рис. 11.2. Реконструированные изображения, полученные с использованием соотно-

шений (11.22) и (11.23). Начальное значение

дг<

такое же, как на рис. 7.5 Д а

Х<*>

ж 1

для всех к.

а ^ оценка xVh б - *W; в -

хРП;

*4/.

Рис. 11.3. Распределения плотностей вдоль 63-го столбца реконструированных изо-

бражений, приведенных иа рис. 11.2.

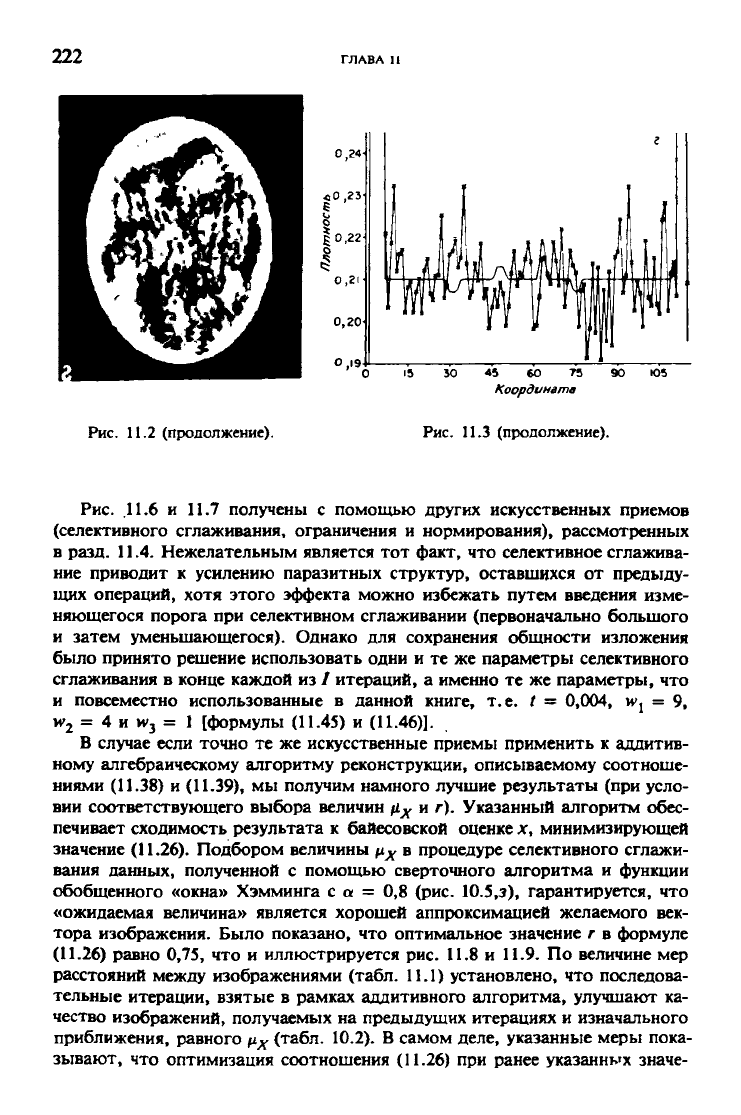
222

ГЛАВА 11

Координата

Рис.

11.2 (продолжение). Рис. 11.3 (продолжение).

Рис.

.11.6 и 11.7 получены с помощью других искусственных приемов

(селективного сглаживания, ограничения и нормирования), рассмотренных

в разд. 11.4. Нежелательным является тот факт, что селективное сглажива-

ние приводит к усилению паразитных структур, оставшихся от предыду-

щих операций, хотя этого эффекта можно избежать путем введения изме-

няющегося порога при селективном сглаживании (первоначально большого

и затем уменьшающегося). Однако для сохранения общности изложения

было принято решение использовать одни и те же параметры селективного

сглаживания в конце каждой из / итераций, а именно те же параметры, что

и повсеместно использованные в данной книге, т.е. / = 0,004, и^ = 9,

и>

= 4 и vv

= 1 [формулы (11.45) и (11.46)].

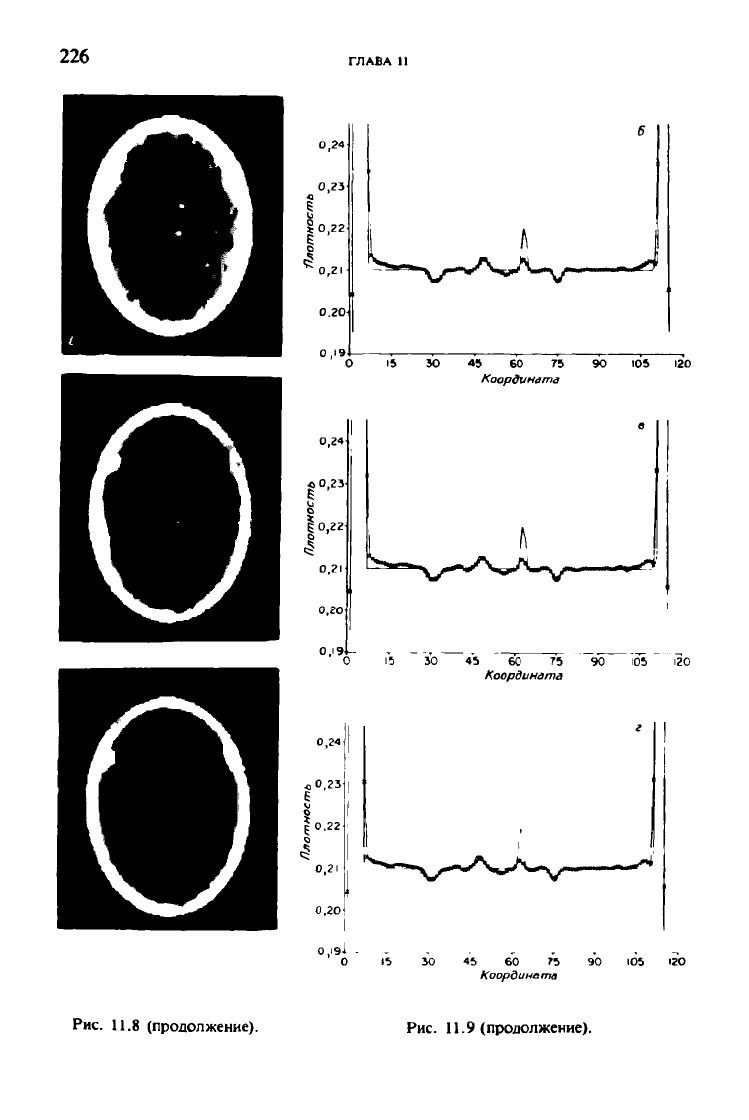
В случае если точно те же искусственные приемы применить к аддитив-

ному алгебраическому алгоритму реконструкции, описываемому соотноше-

ниями (11.38) и (11.39), мы получим намного лучшие результаты (при усло-

вии соответствующего выбора величин \к

и г). Указанный алгоритм обес-

печивает сходимость результата к байесовской оценке

дг,

минимизирующей

значение (11.26). Подбором величины ц.

в процедуре селективного сглажи-

вания данных, полученной с помощью сверточного алгоритма и функции

обобщенного «окна» Хэмминга с а = 0,8 (рис. 10.5

,з),

гарантируется, что

«ожидаемая величина» является хорошей аппроксимацией желаемого век-

тора изображения. Было показано, что оптимальное значение г в формуле

(11.26) равно 0,75, что и иллюстрируется рис. 11.8 и 11.9. По величине мер

расстояний между изображениями (табл. 11.1) установлено, что последова-

тельные итерации, взятые в рамках аддитивного алгоритма, улучшают ка-

чество изображений, получаемых на предыдущих итерациях и изначального

приближения, равного р

(табл. 10.2). В самом деле, указанные меры пока-

зывают, что оптимизация соотношения (11.26) при ранее указанных значе-

|0,гз.

0,21

о,го

0,19;

ОЛ

°'

гу

£0,22

0,21

0,20

0,19

-о 0,23

| 0,22

15 30 45 60 75 90 Ю5 120

Координата

15 30 45 60 75 90 Ю5 «20

Координата

Рис.

11.4.

15 30 45 60 75 90 Ю5 120

Координата

Рис. 11.5.

Рис. 11.4. Реконструированные изображения, полученные аналогично рис. 11.2, за

исключением того, что Л<*> = 0,05 для всех *.

Рис. 11.5. Распределения плотностей вдоль 63-го столбца реконструированных

изображений, приведенных на рис. 11.4.

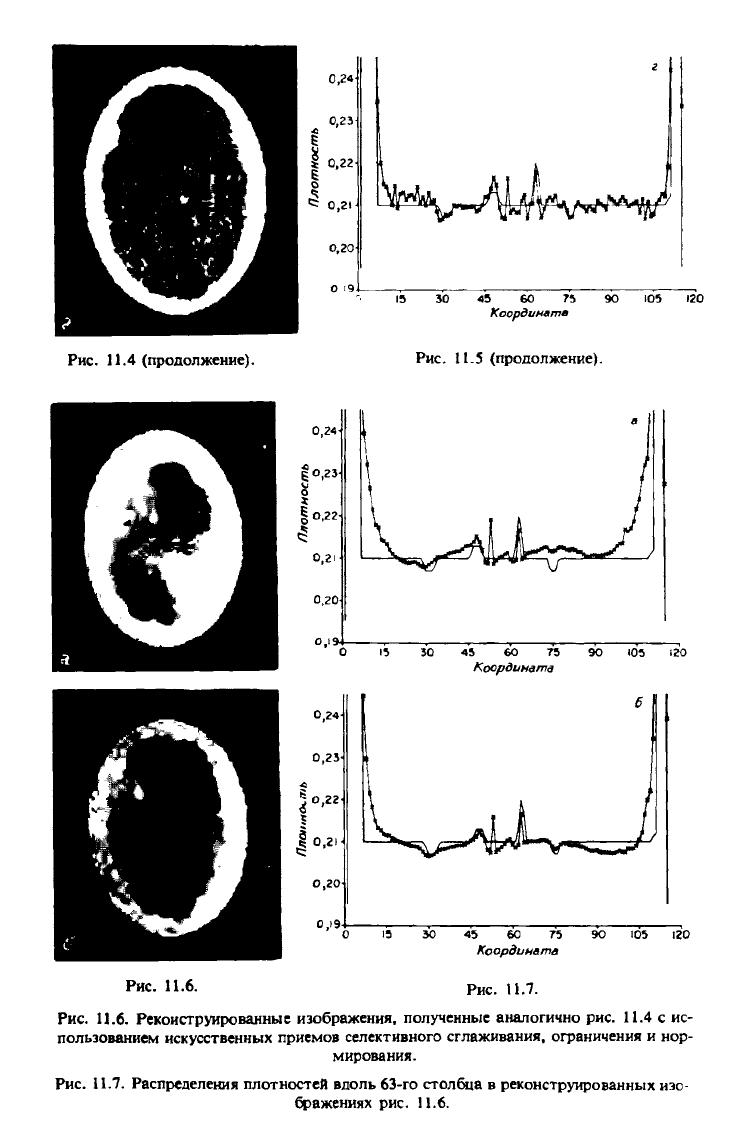
15 30 45 60 75 90 Ю5 «20

Координата

Рис.

11.4 (продолжение).

Рис.

11.5 (продолжение).

Рис.

11.6.

Рис.

11.7.

Рис.

11.6. Рекоиструированные изображения, полученные аналогично рис. 11.4 с ис-

пользованием искусственных приемов селективного сглаживания, ограничения и нор-

мирования.

Рис.

11.7. Распределения плотностей вдоль 63-го столбца в реконструированных изо-

бражениях рис. 11.6.

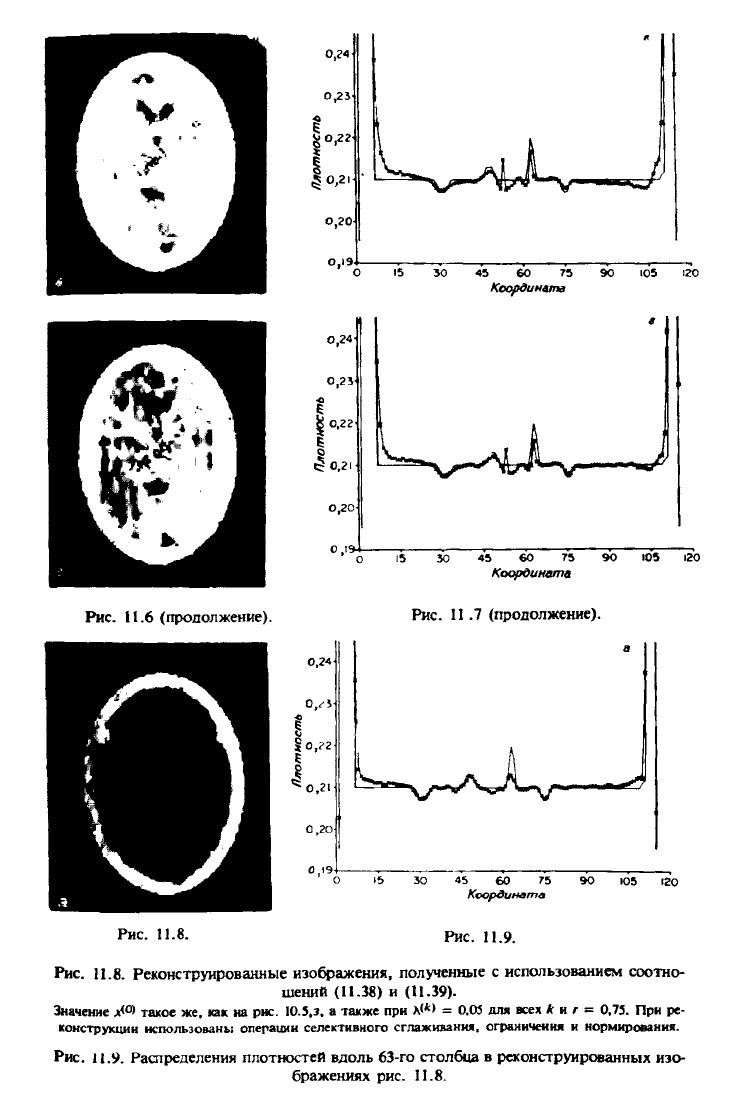
Рис. 11.6 (продолжение).

Рис. 11.8.

0,23'

£0,22

^0,21

0,20

0,19-

°|

0,2з||

■о

£ 0.22

|5 0,21

0,20-jl

0/3

§0,?2

^0,21

0,20

15 30 45 60 75 90 Ю5 120

Координата

15 30 45 60 75 90 105 120

Координата

Рис. 11.7 (продолжение).

1^«->

30 45 60 75 90 Ю5 120

Координата

Рис. 11.9.

Рис. 11.8. Реконструированные изображения, полученные с использованием соотно-

шений (11.38) и (11.39).

Значение л<°) такое же, как на рис. Ю.5.з. а также при А<*> = 0.05 для всех к и г = 0,75. При ре-

конструкции использованы операции селективного сглаживания, ограничения и нормирования.

Рис. 11.9. Распределения плотностей вдоль 63-го столбца в реконструированных изо-

бражениях рис. 11.8.

тз

К)

Плотность

и»

1з<

t*1

АЛГЕБРАИЧЕСКИЕ АЛГОРИТМЫ РЕКОНСТРУКЦИИ ИЗОБРАЖЕНИЙ 227

ниях г и \L

позволяет получить реконструированные изображения более

высокого качества, нежели те, которые мы уже видели до сих пор или уви-

дим после этого в книге. Читателю предоставляется возможность самому

судить о том, соответствует ли мерам расстояния между изображениями

визуальные восприятия этих реконструкций.

Из табл. 11.1 видно, что каждая итерация в алгебраических алгоритмах

реконструкции требует приблизительно 600 с машинного времени, что

близко по порядку величины ко времени полной реконструкции сверточным

алгоритмом. В отличие от четырех обсуждавшихся выше искусственных

приемов дополнительные итерации практически не влияют на качество ре-

конструируемых изображений, поэтому сомнительно, что при этом повы-

шение качества изображений могло бы окупить вложенные затраты. По-

следнее показывает, что в рутинных методах рентгеновской реконструктив-

ной томографии алгебраические алгоритмы реконструкции не могут соста-

вить конкуренцию сверточному алгоритму, однако в тех случаях, когда

конфигурация системы регистрации достаточно специфична (или же малб

число зарегистрированных фотонов), алгебраические алгоритмы могут

быть эффективней сверточного алгоритма.

ПРИМЕЧАНИЯ И ССЫЛКИ

Для целей реконструкции изображений алгебраические алгоритмы впервые были

опубликованы в [52]. Одновременно аналогичный метод реконструктивной томогра-

фии был уже предложен в описании к патенту Хаунсфилда [88], первоначально заре-

гистрированному им в 1968 г. На самом же деле тот простой алгоритм, который

описывается соотношением (11.2), в 1937 г. уже был предложен Качмаржем [94] для

решения систем совместных линейных уравнений. Методическое изложение особен-

ностей алгебраических алгоритмов реконструкции принадлежит Гордону [50]. Мето-

ды,

рассмотренные в данной главе, являются частными случаями так называемых

методов генерации

строк,

предназначенных для решения систем разреженных урав-

нений или неравенств; их обзор содержится в работе [27].

Принятая нами методика изложения релаксационных методов решения систем

уравнений и неравенств основана на работах [71, 85], в которых приведена библио-

графия более ранних работ. Обладающий свойством конечной сходимости метод

ART-3 описан в [63]. Теорема о минимальной норме представляет собой тривиаль-

ное следствие теоремы, которая в теории получила название «проекционная теоре-

ма» (не следует путать ее с теоремой того же названия в теории реконструкции изо-

бражения; для знакомства с первой см. работу [112]). Релаксационный подход к на-

хождению решения с минимальной нормой для системы неравенств приведен в рабо-

те

[106].

Вопрос о том, каким образом указанный подход использовать для рекон-

струкции изображений, был исследован в [73].

Рассмотрение байесовского подхода основано на работах [81, 82]. Во второй из

перечисленных работ приведено детальное рассмотрение вопроса о справедливости

предположений, использованных в байесовском подходе.

Термин «искусственные приемы» впервые введен в [71] для обозначения проце-

дур,

описанных в разд. 11.4. Подробное изложение этих вопросов можно найти в са-

мой работе и библиографии к ней. Алгоритм, позволяющий находить решение с ми-

нимальной нормой для комбинированной системы соотношений (11.40) и (11.47),