Хермен Г. Восстановление изображений по проекциям: Основы реконструктивной томографии
Подождите немного. Документ загружается.

188
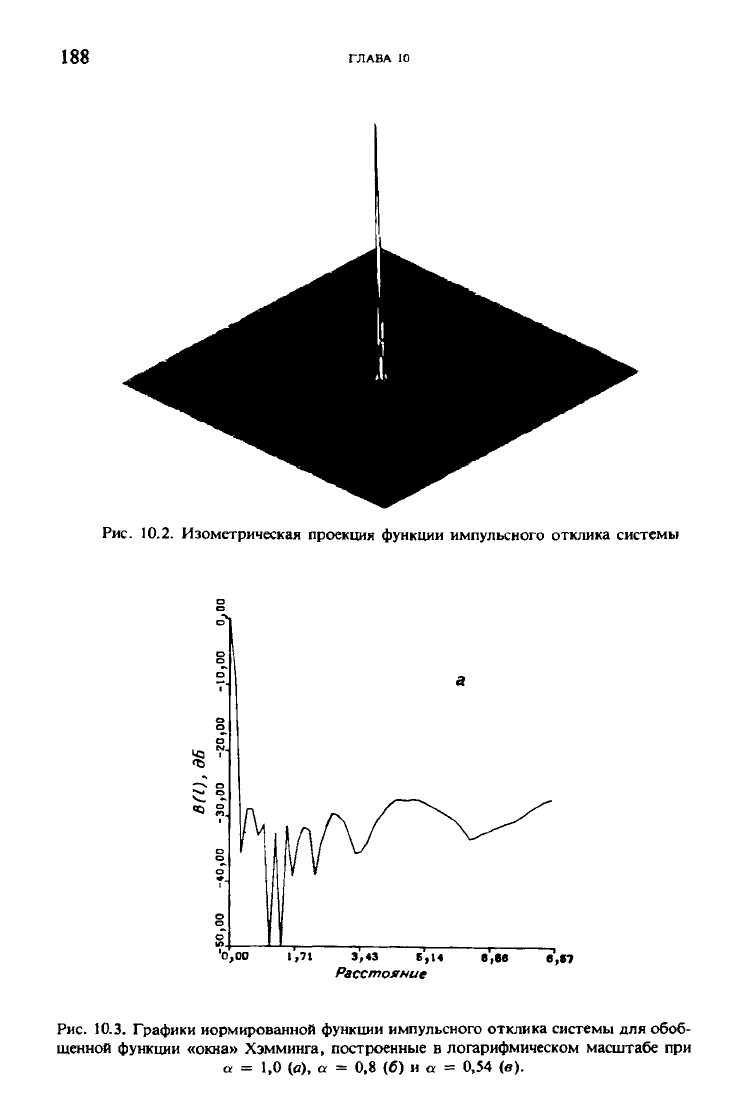
Рис. 10.2. Изометрическая проекция функции импульсного отклика системы
h
'0,00
1,71
3,43 6,14
Расстояние
6,66
6,87
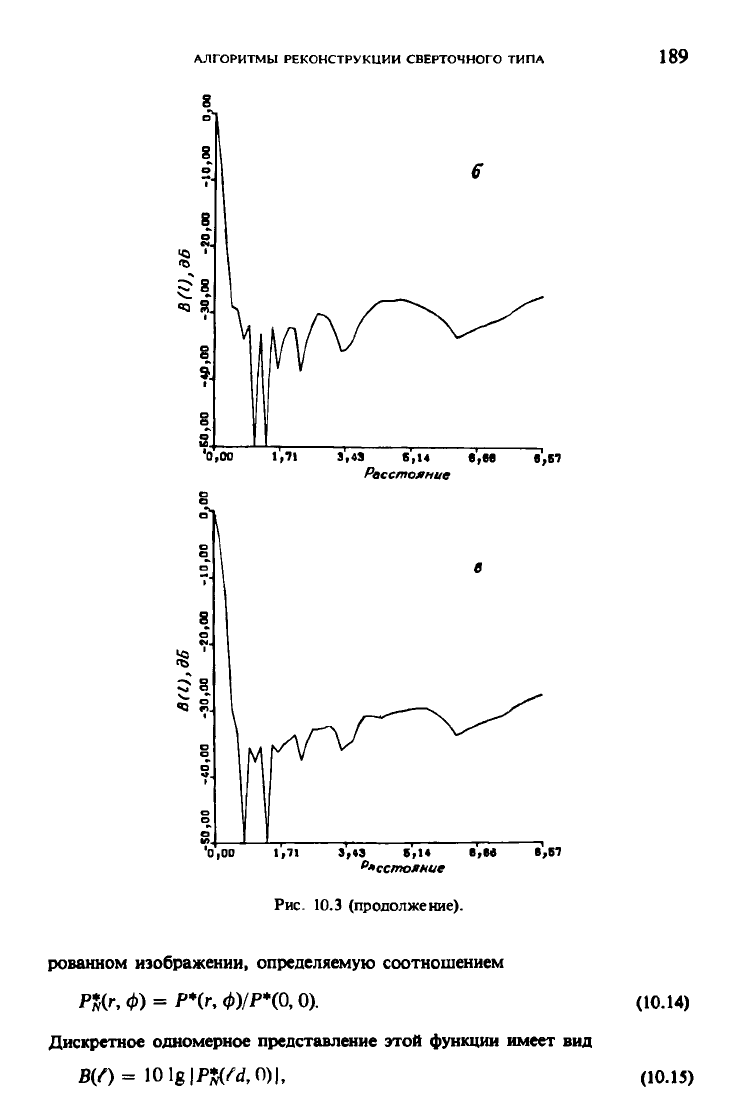
Рис. 10.3. Графики нормированной функции импульсного отклика системы для обоб-
щенной функции «окна» Хэмминга, построенные в логарифмическом масштабе при
а = 1,0 (о), а = 0,8 (б) и a = 0,54 (в).
АЛГОРИТМЫ РЕКОНСТРУКЦИИ СВЕРТОЧНОГО ТИПА
189
'0,00
1,71 Э,4Э 6,14 6,66
Расстояние
'0,00 1,71
3,43 6,14
&*сстояние
6.67
6,64 6,67
Рис. 10.3 (продолжение).
рованном изображении, определяемую соотношением
PJS(r, ф) = Р*(г, </>)/Р*(0, 0). (10.14)
Дискретное одномерное представление этой функции имеет вид
В(0= 101g|PJK«,0)|
f
(10.15)

190
ГЛАВА 10
Ta6.i , ш 10.1.
Критерии качества изображающей системы для функции обобщенного «окна» Хэмминга
пои различных значениях а
1
*
а
Полушири-
на на полу-
высоте
HWHM
Интен-
■снвность
первого
бокового
лепестка
Интенсивность
фона на боль-.
шом расстоянии
от максимума
10
5
X
10
4
X
10
2
х
Х
-^12,0/^
S
1,0
0,5586
-29,945 -27,098
5,6777
9,6478
2,5619
0,2494
0,8 0,5984 -31.820 -27,186 8,6949 8,5270 2,1138 0,1783
0,54 0,8106 -35,505 -27,506
52,0823
9,1819
1,0325
0,1012
') Первые шесть критериев относятся к измерениям функции импульсного отклика (т.е. пока-
зывают способность системы реконструировать полезный сигнал), тогда как седьмой критерий
характеризует способность системы подавлять шумы. Чем меньше значения всех семи показате-
лей,
тем выше качество системы в целом.
где d — шаг между отсчетами в изображении, в нашем случае равный
0,1504 см. Очевидно, что В(0) = 0. При t Ф 0 было бы желательно, что-
бы величина В(() была возможно малой и при f — ос стремилась бы к
нулю. На рис. 10.3 приведены графики для трех выбранных нами функций
«окна».
В табл. 10.1 приведены значения критерия качества системы В(( ), ко-
торый определяется следующим образом (необходимо учитывать, что
меньшие величины более желательны):
а) полуширина функции на полувысоте HWHM — наименьшее положи-
тельное значение 1, для которого справедливо соотношение
Д(0 = lOlgO.5;
б) интенсивность первого бокового лепестка равна В( t ) при наимень-
шем положительном целом значении l, для которого В( t) > В( 1 — 1) и
В( t) > В( I + 1);
в) интенсивность фона (на большом расстоянии от максимума), соот-
ветствующая интенсивности в последней ячейке по оси дг, т.е. в нашем слу-
чае В (57).
Анализируя функцию импульсного отклика системы, сразу замечаем не-
достатки наших критеоиев качества системы в силу их несовместимости.
Хотя первый показатель HWHM при а = 1,0 выглядит предпочтительнее,
чем при а = 0,54, два других показателя (интенсивности первого всплеска
и фона) ведут себя обратным образом, поэтому «оптимальность» той или
иной функции «окна» зависит от выбора соответствующего критерия.

АЛГОРИТМЫ РЕКОНСТРУКЦИИ СВЕРТОЧНОГО ТИПА
191
Развивая эту мысль, рассмотрим следующий способ оценки качества
нормированной функции импульсного отклика. Большие значения интен-
сивности в непосредственной близости от самой точки считаются «прием-
лемыми», поскольку означают простое размытие изображения. По мере
отдаления от точки большие значения интенсивности становятся все менее
желательными, поскольку означают нечто большее, чем размытие или рез-
кие колебания. Однако существенные значения на слишком большом отда-
лении от точки нельзя связать с точкой, как и те артефакты, которые, воз-
можно, созданы деталями, не лежащими в плоскости исследуемого сече-
ния,
и поэтому этот эффект не может исказить медицинский диагноз. Се-
мейство приемлемых функционалов качества системы &
R
для нормирован-
ной функции импульсного отклика можно определить следующим образом:
$RP%
= f f \гРЦг
ч
ф)\
2
г dr
(1ф.
(10.16)
Jo Jo
Как и в случае ранее введенных критериев качества, меньшим значениям
^Рдг соответствует более высокое качество.
В табл. 10.1 приведены критерии качества для функций импульсного от-
клика при а = 1,0, 0,8 и 0,54 и трех различных величинах R. Из таблицы
видно, что об оптимальности каждой из функций «окон» можно говорить
при соответствующем выборе величины Я.
К проблеме выбора функции «окна» можно подойти с совершенно раз-
ных позиций. Если задать нормированную функцию импульсного отклика,
то можно получить соответствующую (или близкую) к ней функцию «ок-
на». Однако из приведенного выше обсуждения недостатков критериев ка-
чества по функции импульсного отклика следует, что данный способ синте-
за функции «окна» не гарантирует достижения высокого качества рекон-
струированного изображения. При этом центр тяжести проблемы смеща-
ется с вопроса «какая функция «окна» обеспечивает высококачественную
реконструкцию?» на вопрос «функция импульсного отклика какого вида
обеспечивает высококачественную реконструкцию?» Поскольку наиболее
эффективным методом, в рамках которого можно ответить на первый во-
прос, является метод спектрального разложения (разд. 8.6), то становится
не совсем ясным, какую пользу можно получить от подобной замены проб-
лем.
10.4.
РЕКОНСТРУКЦИЯ ШУМОВОЙ СОСТАВЛЯЮЩЕЙ ИЗОБРАЖЕ-
НИЯ
Помимо функции импульсного отклика, эффективность алгоритма ре-
конструкции определяется способностью системы противостоять воздейст-
вию шума, содержащегося в исходных данных. Предположим, что проек-
ции искажены аддитивным шумом. Благодаря линейности операции сверт-

192
ГЛАВА 10
ки реконструированное изображение представляет собой сумму собственно
изображения и реконструкции его шумовой составляющей. По этой причи-
не ниже мы отдельно рассмотрим влияние алгоритма реконструкции на
шумовые характеристики изображения.
Чтобы получить некоторое представление о соотношениях, связываю-
щих шумовые характеристики реконструированного изображения с шумо-
выми характеристиками исходных данных, проведем исследование особен-
ностей реконструкции на весьма простой, но не реализуемой в имеющихся
приложениях модели шума, а именно предположим, что каждое измерение
g(n\
9
тД) представляет собой независимую выборку одной и той же слу-
чайной
•
величины R, причем ее математическое ожидание ц
р
= 0 (разд.
1.2). Таким образом, реконструированное значение интенсивности в точке-с
координатами г, ф, определяемое соотношением (10.13), также является
случайной величиной, которую мы обозначим через F*(r
9
ф). Легко пока-
зать,
что
n
F
*,
r
фу
= 0; другими словами, это означает, что если шумовая
составляющая исходных данных имеет нулевое среднее значение, то и ре-
конструированное значение шума в этой же точке также имеет нулевое
среднее. Дисперсия случайной величины
У
F
*,
r
ф)
зависит от ряда парамет-
ров,
таких, как дисперсия исходных данных V
Rl
вид сворачиваемых функ-
ций <?
(1)
и <?
(2
\ используемых на стадии реконструкции, вид интерполяцион-
ной функции ф, используемой в формуле (10.13), число ракурсов М
%
шаг
между отсчетами по углу
X
и положение точки г, ф. Точная формула имеет
вид
[C(r,0)]
2
F
R
, (10.17)
где
;2
Л
2 М-1 1 N Г JV "12
Ю-.
Ф»>
-
яд,
Z
^1,11*V
-
■«*,..]
•
О"*
И
Чп\п = Я
{1)
((п - n)A)cos пХ + q
{2)
((ri - n)A)cos rik (10.19)
Для определения чувствительности алгоритма реконструкции к воздей-
ствию шумов требуются не оценки в отдельных точках изображения, а
обобщенная мера влияния шумов. Один из способов получения подобной
меры состоит в усреднении величины
С(г
%
ф) по ряду точек с координатами
г,
ф
%
что и было сделано в ходе экспериментов по реконструкции шумовой
компоненты по формулам (10.17) — (10.19) при использовании 49 значений
на сетке из 7 х 7 элементов с шагом 2,8576 см. Результаты экспериментов
сведены в столбец табл. 10.1, обозначенный буквой S. Усредненное значе-
ние стандартного отклонения в реконструированном изображении равно
SVT^
[формула (10.17)].
С учетом анализа, проведенного в разд. 8.6, оказывается неудивитель-
ным,
что функция «окна» с максимально подавленными высокочастотны-

АЛГОРИТМЫ РЕКОНСТРУКЦИИ СВЕРТОЧНОГО ТИПА
193
ми компонентами (при
а = 0,54)
является наиболее устойчивой
к
воздейст-
вию шума.
Отметим,
что, в то
время
как
величина
S
показывает, каким образом
различные функции «окна» способны подавлять
шум при
реконструкции
отдельных точек,
она тем не
менее ничего
не
говорит
о
том, как скоррели-
рован
шум в
реконструированном изображении. Может, например, полу-
читься
так, что
функция «окна» имеет малое значение параметра
S и тем
не менее является неприемлемой, если исходные данные сильно зашумле-
ны,
поскольку
при
этом возникают структурированные шумы,
т.е.
шумы,
которые особо влияют
на
реконструированное изображение
в
соседних точ-
ках, давая эффект, весьма сходный
с
эффектом возникновения ложных
структур
в
относительно больших областях изображения.
10.5.
ПОВТОРНОЕ РАЗБИЕНИЕ
Как было показано
в
разд.
8.1,
луч
с
координатами
а, 0 в
системе веер-
ного пучка соответствует точке
в
системе
( f,
0)-координат.
В гл. 6 уже
был использован сверточный алгоритм
для
вычисления обратного преоб-
разования Радона функции
р
двух вещественных переменных
по
вычислен-
ным
ее
значениям
в
точках
ud, i/Г, где
—
U ^ и ^ U и 0 ^ v ^ V
—
1,
причем
Ud > Е и VT = х.
Можно считать [формула
(10.2)],
что
исходные
данные
g(n X,
/иД),
где - N < п ^ N, 0 ^ т ^ М - 1,
причем
N\ ^ б и
А/А
= 2х,
зарегистрированные
в
веерном пучке, позволяют получать значе-
ния функции
р в
соответствии
со
следующим правилом:
p(D
sin
пЯ,
тА + пА) =
д(пХ,
тА).
(10.20)
где
- N ^ л ^ N, 0 < т ^ М - 1, Ud > £, УГ = х. На
рис. 10.4 показа-
ны точки
в
системе координат
/, 0, в
которых
по
формуле (10.20) определя-
лись значения функции
р (рис. 6.2).
Переписывая соотношение (6.5), получаем
p(D
sin
пЯ,
тА +
иЯ)
= p(D
sin(
—
и)Я, wA
+ иЯ + я)
=
p(D
sin( -и)Я,
wA + пЯ - я).
(10.21)
Таким образом, функция p(Dsinп\,
тА + п\) в
формуле (10.20)
при
значе-
ниях аргумента
тА + лХ,
лежащих
вне
интервала
0+ т,
дает
нам
значе-
ния функции
р{ f, в) при t =
DsinnX
для
значений
л, для
которых
-7У<л<7У,иО<0<т.
Подводя итоги, заметим,
что
проекции, полученные
в
схеме
с
веерным
пучком, дают
нам
значения
р(1
п
, 0
П k
)
t
где /„ =
DsinnK
- N ^ л ^ 7V,
0
^
^п
k
< Т
•
по
которым необходимо найти значения
p(nd
%
vT) при
-С/<и<(/и0<|;<И-1.
Одним
из
способов нахождения указанных значений является описанный
194
ГЛАВА 10
-DimNX
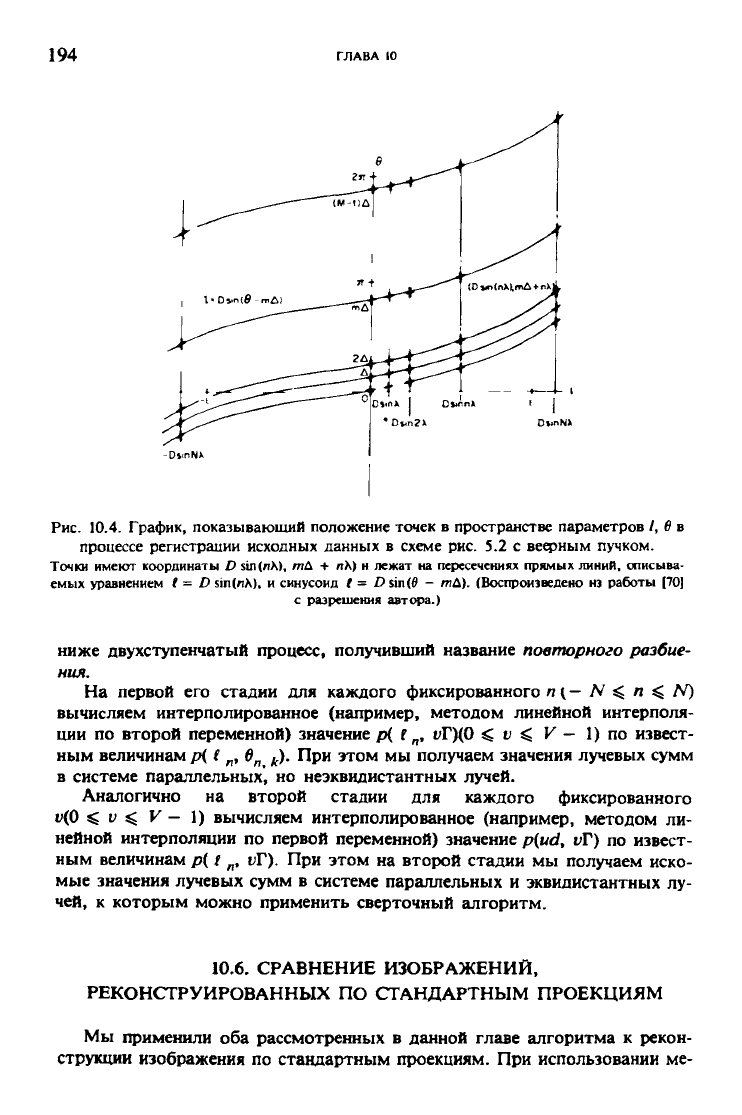
Рис. 10.4. График, показывающий положение точек в пространстве параметров /, в в
процессе регистрации исходных данных в схеме рис. 5.2 с веерным пучком.
Точки имеют координаты D sin(nX), тА + лХ) н лежат на пересечениях прямых линий, описыва-
емых уравнением ( = D sin(nX), и синусоид / = £>sin(0 - гпД). (Воспроизведено нз работы [70]
с разрешения автора.)
ниже двухступенчатый процесс, получивший название повторного разбие-
ния.
На первой его стадии для каждого фиксированного п{— N ^ п < ДО
вычисляем интерполированное (например, методом линейной интерполя-
ции по второй переменной) значение р( I
п
, tT)(0 ^ v < V
—
1) по извест-
ным величинам р{ (
л
, в
п к
). При этом мы получаем значения лучевых сумм
в системе параллельных, но неэквидистантных лучей.
Аналогично на второй стадии для каждого фиксированного
v(0 ^ v < V - 1) вычисляем интерполированное (например, методом ли-
нейной интерполяции по первой переменной) значение p(ud, vT) по извест-
ным величинам р( t
п%
vT). При этом на второй стадии мы получаем иско-
мые значения лучевых сумм в системе параллельных и эквидистантных лу-
чей,
к которым можно применить сверточный алгоритм.
10.6.
СРАВНЕНИЕ ИЗОБРАЖЕНИЙ,
РЕКОНСТРУИРОВАННЫХ ПО СТАНДАРТНЫМ ПРОЕКЦИЯМ
Мы применили оба рассмотренных в данной главе алгоритма к рекон-
струкции изображения по стандартным проекциям. При использовании ме-

АЛГОРИТМЫ РЕКОНСТРУКЦИИ СВЕРТОЧНОГО ТИПА
195
Таблица 10.2
Мера расстояния между реконструированными изображениями рис. 10.5
Алгоритм реконструирования a d г е t
Сверточный алгоритм для
1.0
0,1038
0,0447
0,0597
158
параллельного пучка (с
0,8
0,1278
0,0510
0,0756 164
повторным разбиением данных)
0,54
0,1629
0,0602
0,0962 162
Сверточный алгоритм для
1.0
0.0918
0.0422
0,0500
835
веерного пучка (без
0,8
0,1162
0,0480 0,0674 847
сглаживания данных)
0,54
0,1545
0,0570
0,900
863
Сверточный алгоритм для
1.0
0,0913 0,0406 0,0497
841
веерного пучка (со сгла-
0,8
0,1159
0,0465 0,0674
853
живанием данных)
0,54 0,1544
0,0558
0,900
868
тода повторного разбиения образуется стандартная конфигурация системы
с параллельным пучком (разд. 5.6). В обоих алгоритмах были применены
линейная интерполяция данных и функция обобщенного «окна» Хэмминга
при трех значениях параметра а (1,0, 0,8 и 0,54). Результаты реконструк-
ции представлены на рис. 10.5 и 10.6, а также в табл. 10.2. Был применен
алгоритм нелинейного сглаживания при значении порога, равном 0,04, и
весовых коэффициентах, составляющих 9, 4 и 1 (смысл этих понятий станет
ясен из разд. 11.4) для данных, обработанных сверточным алгоритмом
для веерного пучка. Полученные при этом результаты приведены здесь же.
Алгоритм, развитый в гл. 5 для анализа различных физических источников
погрешности, также является сверточным алгоритмом для веерного пучка,
использующим функцию обобщенного «окна» Хэмминга с а = 0,8, и алго-
ритм нелинейного сглаживания с описанными выше параметрами.
Здесь мы можем привести некоторые выводы из полученных результа-
тов.
Во-первых, можно отметить небольшие различия между реконструиро-
ванными изображениями, полученными при помощи сверточного алгорит-
ма для веерного пучка, с одной стороны, и алгоритма с повторным разбие-
нием и последующей операцией свертки для параллельного пучка — с дру-
гой;
поэтому можно утверждать, что выбор алгоритма не определяет ка-
чества реконструкции.
Проведенный нами хронометраж показал, что операции повторного
разбиения и сворачивания для параллельного пучка требуют меньше ма-
шинного времени, чем сверточный алгоритм для веерного пучка. Это не-
удивительно, так как в последнем используется вдвое большее число ракур-
сов,
а также операций умножения на весовые коэффициенты на стадии об-
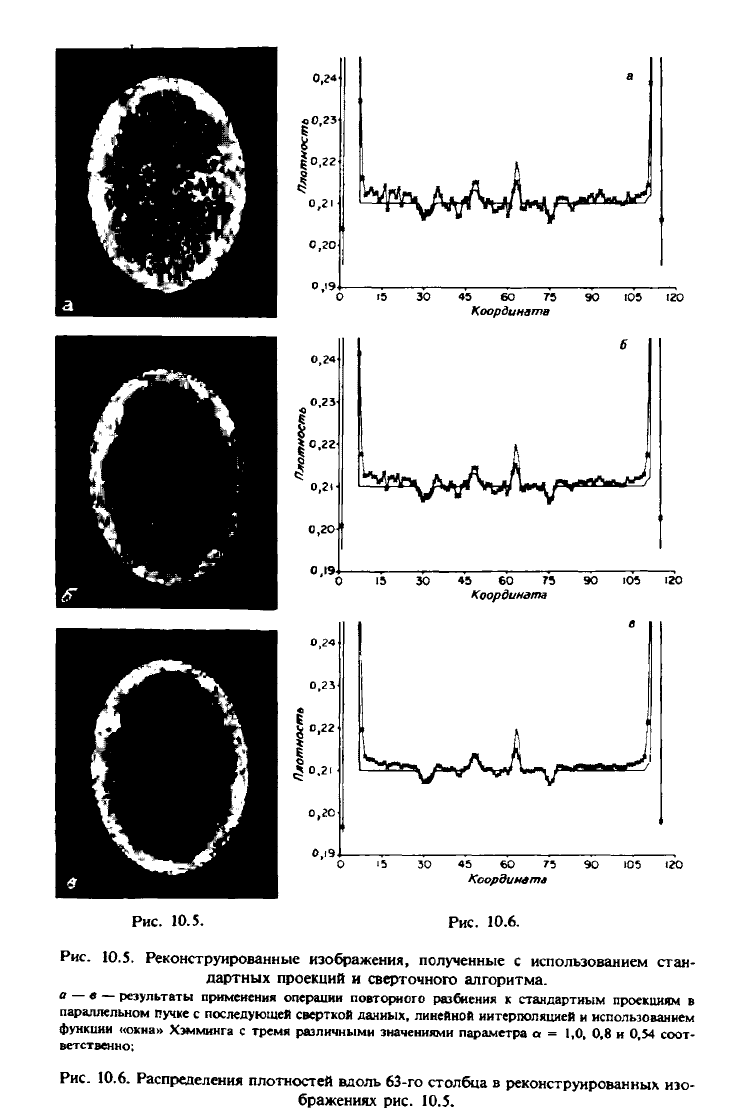
Рис. 10.5.
g0,23
|о,22{
0,19
0,24
0,23
| 0,22
I
0,2«
°»
20
1t
0,191
I
0,22]
5
0,21
0,20
0.i9
45 60 75 90 105 120
Координата
30 45 60 75 90 Ю5 120
Координата
45 60 75
Координата
Рис. 10.6.
90 Ю5 120
Рис. 10.5. Реконструированные изображения, полученные с использованием стан-
дартных проекций и сверточного алгоритма.
а
—
в
— Результаты применения операции повторного разбиения
к
стандартным проекциям
в
параллельном пучке
с
последующей сверткой данных, линейной интерполяцией
и
использованием
функции «окна» Хэмминга
с
тремя различными значениями параметра
а = 1,0, 0,8 и 0,54
соот-
ветственно;
Рис.
10.6.
Распределения плотностей вдоль 63-го столбца
в
реконструированных изо-
бражениях
рис. 10.5.
0,23
J
I
°'
22
I
^ 0,21
0.20H
^\^J^ri^
0,24
О
£ 0,22-^
$
0,2»
0,19
0.24-Ц
0,23
I
^ 0.2 f
0,20 A
0,19
15 30 45 60 75 90 105 120
Координата
15 30 45 60 75 90 105 120
Координате
15
30 45 60 75 90 105 " 120
Координата
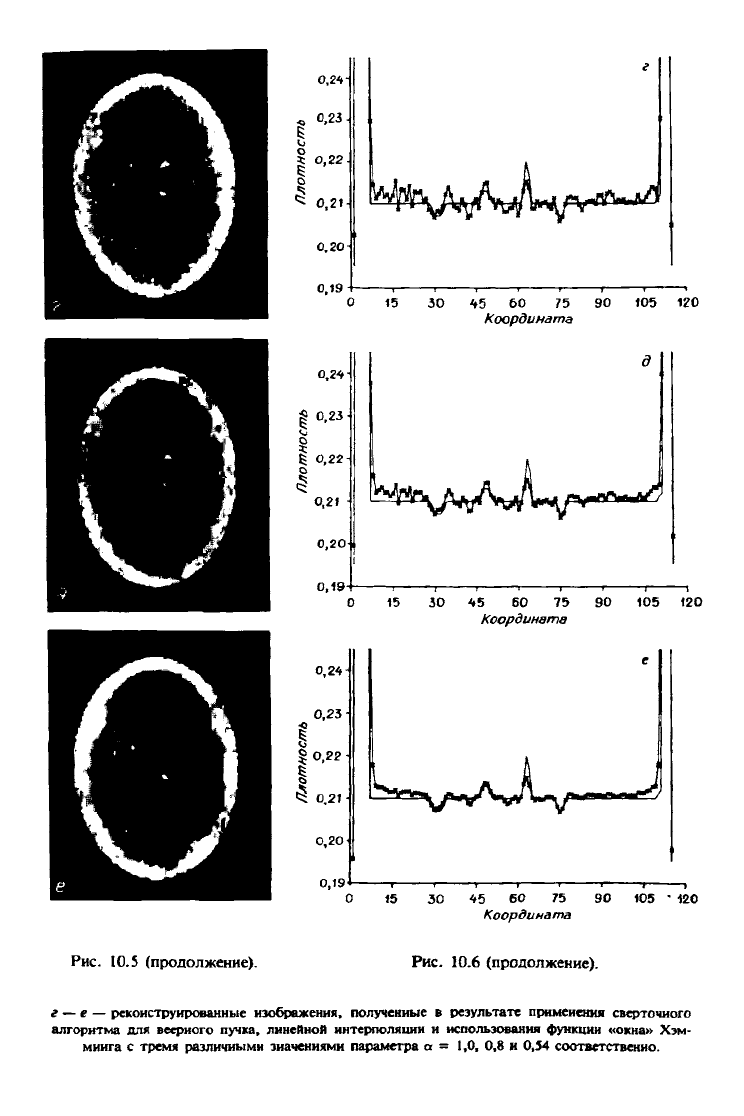
Рис. 10.5 (продолжение).
Рис. 10.6 (продолжение).
г — е — реконструированные изображения, полученные в результате применения сверточиого
алгоритма для веерного пучка, линейной интерполяции и использования функции «окна» Хзм-
миига с тремя различными значениями параметра а = 1,0, 0,8 и 0,54 соответственно.
