Хермен Г. Восстановление изображений по проекциям: Основы реконструктивной томографии

Подождите немного. Документ загружается.

138

ГЛАВА 8

ла (8.31) и рис. 8.3, в особенности ограниченную по частоте функцию «ок-

на»].

Окончательно, если для некоторого семейства функций «окна» [F

)

выбор величины А в виде А

< \/d представляется идеальным, то, вероят-

но,

существует и другое семейство функций «окна» (G

}, такое, что

= F

. Таким образом, в дальнейшем мы будем предполагать, что

А = l/d, т.е. ширина полосы частот функции «окна» обратно пропорцио-

нальна шагу между отсчетами.

Предполагая, что замечание о соответствии функций q и &~

остает-

ся в силе [Ф определяется формулой

(8.31)],

мы тем самым оставляем от-

крытым вопрос о выборе функции «окна» F

(U). Метод регуляризации, из-

ложенный в разд. 8.4, показывает, что для рассмотренных семейств функ-

ций «окна» оптимальная предельная величина Ф дается выражением

Ф(С/)

—

(С/). Можно, таким образом, показать, что ограниченная по часто-

те функция «окна», которая получается при подстановке в Ф его идеально-

го значения в диапазоне до А/2, может оказаться наилучшей. Однако в ме-

тоде регуляризации используется предположение об идеальных исходных

данных. Как было видно из приведенного выше анализа свойств функции

ее значения вблизи пороговой величины l/2d могут быть неточными,

что и учитывается в методе регуляризации; кроме того, поскольку в этом

случае мы будем полагать F

(U) = IC/I, функция F

будет умножаться на

Fj,

причем в качестве F, берется наибольшее из минимально возможных

значений функции.

Из всего сказанного можно сделать следующий вывод. Если набор ис-

ходных данных достаточно «хорош», а фурье-образ &р

достаточно точно

ограничен по частоте величиной \/d, то достаточно выбрать q таким, что-

бы равенство [F

q\(U) = F

(U) =

С/1

было справедливо в диапазоне про-

странственных частот

—

1/2*/ ^ U < \/2d. Однако если исходные данные

сильно зашумлены или возникают ложные частоты на пространственных

частотах вблизи значения \/2d

то выбор функции F

(U) с малым значени-

ем вблизи \/2d представляется наиболее разумным для получения хороших

результатов, поскольку это исключает дальнейшее перемножение искажен-

ных амплитуд гармоник на пространственных частотах вблизи l/2d с отно-

сительно большими значениями

С/1.

Точный выбор фильтра должен зави-

сеть от схемы получения исходных данных

типа реконструируемого объекта.

Теперь мы подошли к рассмотрению функции F

. В идеальных условиях

она везде имеет величину порядка единицы, однако на практике при выбо-

ре функции необходимо учитывать различные факторы. Мы предполагали,

что произведение [&p

](U) х l^q^U) приближенно равно нулю при

IC/I > \/2d. Однако как F,, так и F

являются периодическими функциями

с периодом l/d, и таким образом, при IC/I > l/2d маловероятно, что их

произведение было близко к нулю. Функцию F^(U) можно использовать в

качестве средства коррекции спектра, и при этом желательно выбирать ве-

личину

1/^(С/)1

достаточно малой при IC/I > l/2d. Даже при IC/I < \/2d

нежелательно иметь функцию F

}

(U) порядка единицы, поскольку функции

(C/) и F

(U) можно использовать для подавления искаженных значений

СВЕРТОЧНЫЙ АЛГОРИТМ РЕКОНСТРУКЦИИ

159

'0,00 1,00 2,00 3,00 4,00

Частота

1,00 2,00 3,00

Частота

4,00

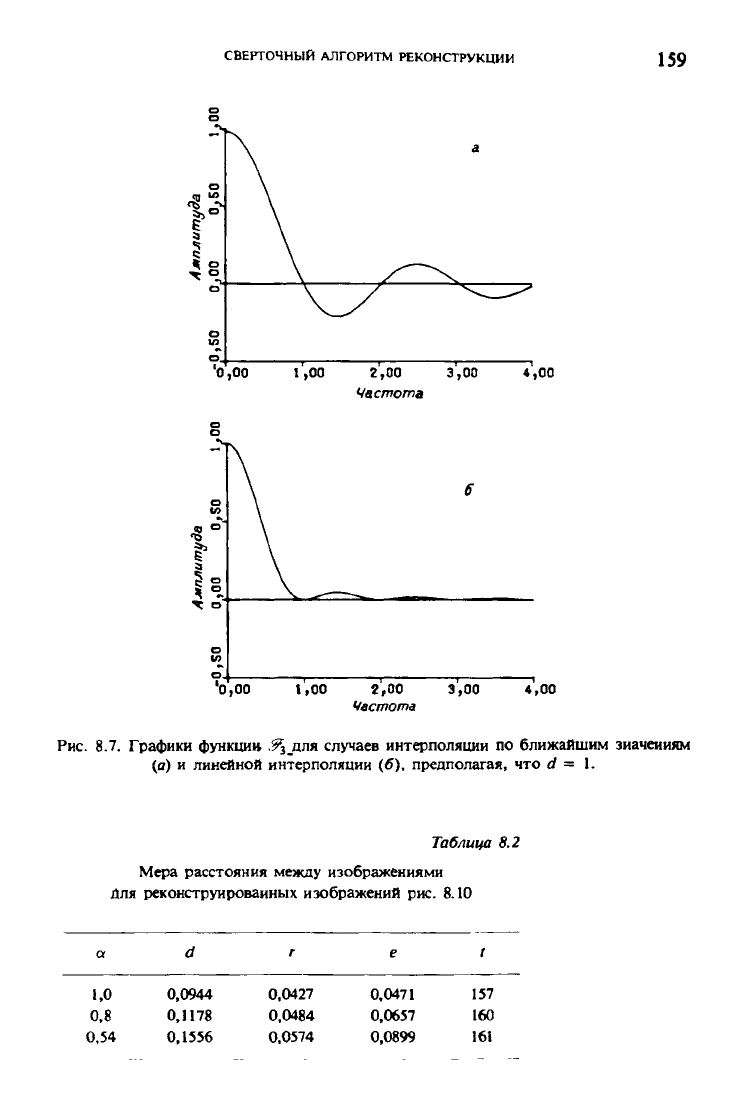
Рис. 8.7. Графики функции ^з_для случаев интерполяции по ближайшим значениям

(а) и линейной интерполяции (б), предполагая, что d = 1.

Таблица

8.2

Мера расстояния между изображениями

Для реконструированных изображений рис. 8.10

1.0

0,0944

0,0427

0,0471

157

0,8

0,1178

0,0484 0,0657

160

0,54

0,1556

0.0574

0,0899

161

0,2*

1°,22

0.201

0,24

0,23

I 0,22

0,20

0,.*

^=^^

Рис. 8.8.

15 30 45 60 75 90 105 120

Координата

Рис. 8.9.

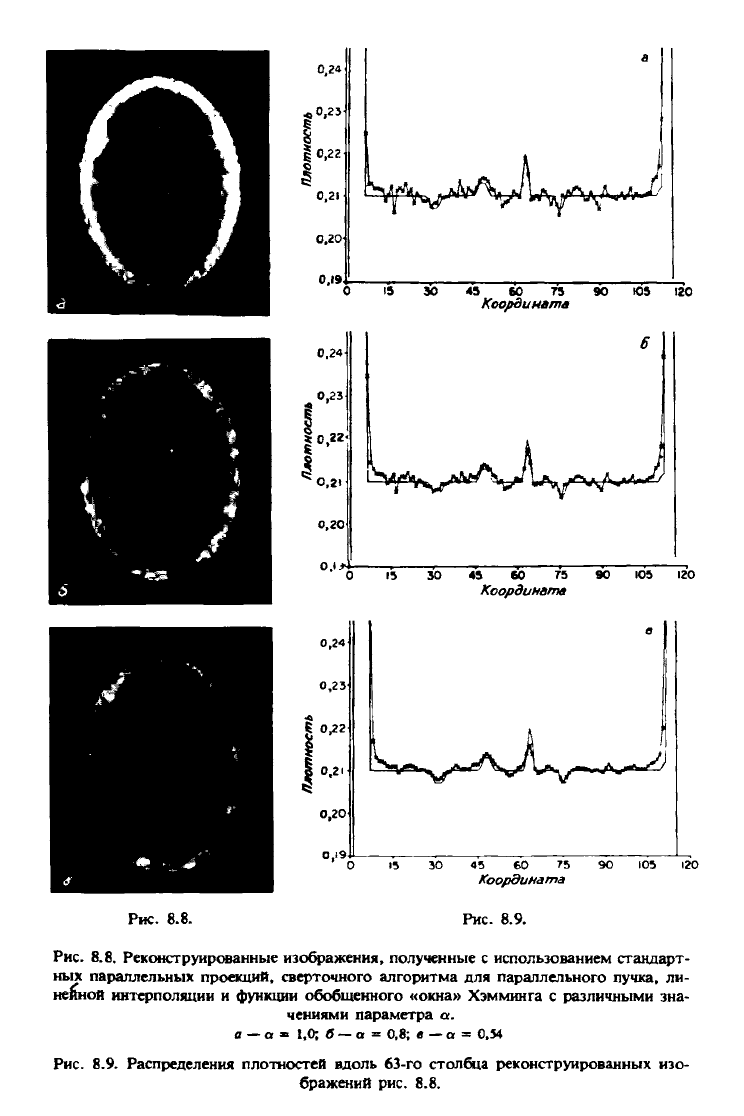
Рис. 8.8. Реконструированные изображения, полученные с использованием стандарт-

ных параллельных проекций, сверточного алгоритма для параллельного пучка, ли-

нейной интерполяции и функции обобщенного «окна» Хэмминга с различными зна-

чениями параметра а.

—

1,0; б

—

а = 0,8; в

—

а = 0.54

Рис. 8.9. Распределения плотностей вдоль 63-го столбца реконструированных изо-

бражений рис. 8.8.

СВЕРТОЧНЫЙ АЛГОРИТМ РЕКОНСТРУКЦИИ

161

функции F

}

(U) на пространственных частотах \U\ порядка l/2d. Следова-

тельно, оптимальная функция F

— это функция, равная единице в начале

координат, спадающая до величины l/2d и близкая к нулю за пределами

значения 1/2*/.

На рис. 8.7 приведен график функции F^(U) для случая интерполяции по

ближайшим значениям и для метода линейной интерполяции. С учетом

сделанных замечаний не вызывает удивления тот факт, что линейная ин-

терпретация обычно дает лучшую реконструкцию, чем метод интерполя-

ции по ближайшим значениям.

Проиллюстрируем приведенное выше рассмотрение реконструирован-

ными изображениями, полученными с использованием стандартных проек-

ций в параллельном пучке. Дополнительный анализ сворачивающей функ-

ции будет приведен в разд. 10.2.

На рис. 8.8 представлены результаты реконструкции с использованием

линейной интерполяции и функции обобщенного «окна» Хэмминга при раз-

личных значениях параметра а. Случай а = 1 соответствует прямоуголь-

ной функции «окна», ограниченной по частоте; при этом подавления про-

странственных частот вблизи U = 1/2*/ не происходит. Случай а = 0,54

представляет другой крайний случай, соответствующий «окну» Хэмминга.

При а

—

0,8 имеет место промежуточный случай. Отметим, что меньшим

значениям а соответствуют изображения, воспринимаемые как более рав-

номерные (за счет подавления высокочастотных гармоник), однако при

этом на изображении в шумах можно не заметить опухоль. На рис. 8.9 по-

строено распределение значений плотности вдоль 63-го столбца, а в

табл.

8.2 приведены данные по измерению расстояний по реконструирован-

ному изображению и по времени вычислений.

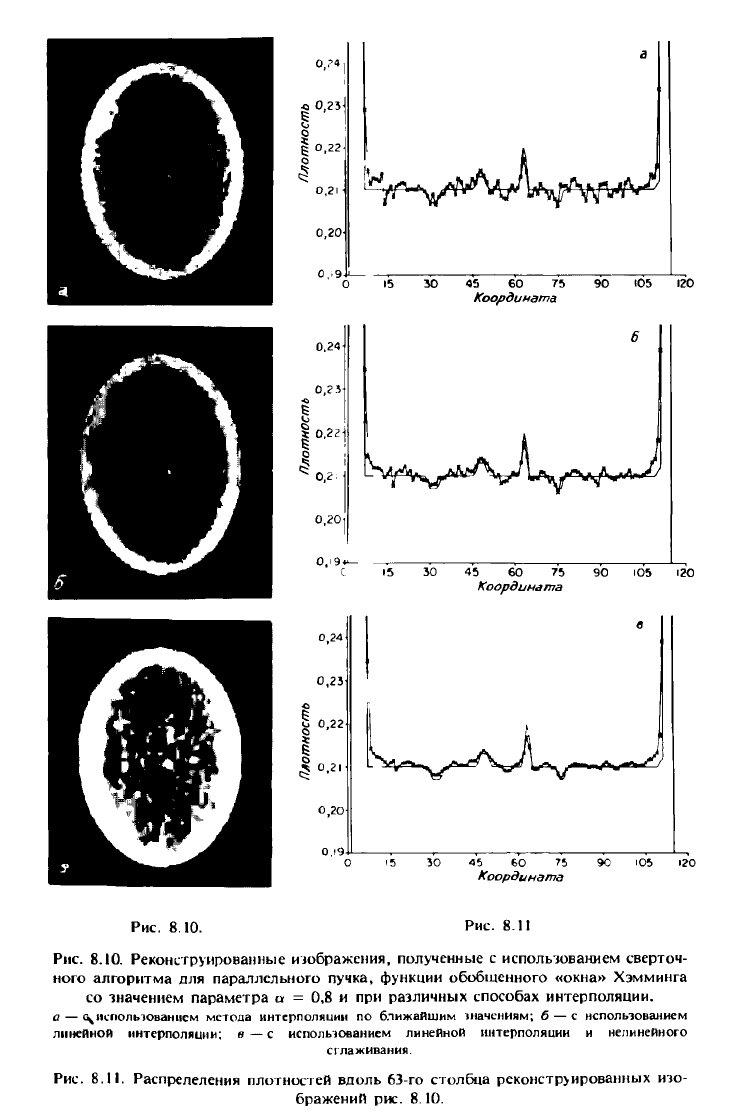
На рис. 8.10 и 8.11, а также в табл. 8.3 дано сравнение методов интер-

поляции (линейной и по соседним значениям) при фильтрации фильтром

Хэмминга с а = 0,8. Из обоих рисунков видно, что первый метод интерпо-

ляции заметно превосходит второй, однако измерения расстояний d и е по

изображению, наоборот, свидетельствуют о преимуществах способа интер-

Таблица 8.3

Мера расстояния между изображениями для реконструированных

изображений рис. 8.10

Метод обработки d г е t

Интерполяция по ближайшим

значениям 0,1168 0,0589 0,0652 144

Линейная интерполяция 0,1178 0,0484 0,0657 160

Нелинейное сглаживание 0,1175 0,0470 0,0657 166

■Q

0,23

| 0,22

So.22

15 30 45 60 75 90 Ю5 120

Координата

L-a^J

15 30 45 60 75 90 105 120

Координата

гъ\\

t 0,22

| 0.21

**s)

15 30 45 60 75 90 Ю5 1?0

Координата

Рис. 8.10.

Рис. 8.11

Рис. 8.10. Реконструированные изображения, полученные с использованием сверточ-

ного алгоритма для параллельного пучка, функции обобщенного «окна» Хэмминга

со значением параметра а = 0,8 и при различных способах интерполяции.

a — \ использованием метода интерполяции по ближайшим значениям; б— с использованием

линейной интерполяции; в — с использованием линейной интерполяции и нелинейного

сглаживания.

Рис. 8.11. Распрелеления плотностей вдоль 63-го столбца реконструированных изо-

бражений рис. 8.10.

СВЕРТОЧНЫЙ АЛГОРИТМ РЕКОНСТРУКЦИИ

163

поляции по соседним значениям. Причина состоит в том, что оба эти изме-

рения сильно зависят от точности реконструкции черепа. Линейная интер-

поляция обеспечивает меньшую точность, чем метод интерполяции по со-

седним значениям в области изображения, занимаемой черепом, однако в

области, расположенной внутри черепа, ситуация обратная. Эти выводы —

яркий пример специфических особенностей реконструктивной томографии.

а именно надлежащий выбор оптимальных значений свободных парамет-

ров зависит от того, какую информацию требуется извлечь из реконструи-

рованного изображения. Третий пример в приведенной серии изображений

представляет собой копию стандартной реконструкции по методу, исполь-

зующему линейную интерполяцию в сочетании с нелинейным сглаживани-

ем (гл. 5). Данная процедура обработки изображений будет рассмотрена в

разд.

11.4.

8.7. В ЧЕМ ЖЕ ПРИЧИНА ПОПУЛЯРНОСТИ

СВЕРТОЧНОГО АЛГОРИТМА?

Сверточный алгоритм наиболее широко используется при реконструк-

ции изображений по исходным данным, получаемым в системе регистра-

ции с параллельным пучком. Имеется много аргументов в пользу этого ал-

горитма.

Основное преимущество алгоритма — это простота вычислений. Как

это было показано в разд. 8.3, затраты машинного времени и объем памя-

ти с использованием сверточного алгоритма исключительно малы даже

при работе на универсальных ЭВМ. Анализ показывает, что сравнительно

просто построить специализированное вычислительное устройство, кото-

рое весьма эффективно реализует данный сверточный алгоритм. По исход-

ным данным о каждом ракурсе могут независимо выполняться операции

свертки и обратного проецирования для другого ракурса, а результирую-

щее изображение представляет собой просто сумму подобным образом об-

работанных ракурсов. В существующих в настоящее время сканерах рекон-

струкция большеформатных изображений (состоящих, например, из

512 х 512 элементов) осуществляется по многим (порядка 500) ракурсам в

течение промежутка времени менее 1 мин.

Качество реконструкции в сверточном алгоритме в среднем практически

такое же, как и у других алгоритмов, а часто даже превышает его. Это не

означает, что не существует случаев, когда изображения более высокого ка-

чества получаются без помощи сверточного алгоритма, а с помощью дру-

гих алгоритмов реконструкции, однако, когда имеется большое количество

достаточно точных исходных данных (по-видимому, рентгеновскую томо-

графию можно отнести к этой категории), сверточный атгоритм является

наиболее эффективным по сравнению с другими алгоритмами.

Научная и техническая подготовка по физике и электротехнике у боль-

шинства специалистов, занимающихся разработкой томографической аппа-

ратуры, также способствует распространению сверточного алгоритма. Тот

анализ, который был проведен в последнем разделе главы с использовани-

164

ГЛАВА 8

ем преобразования Фурье для пояснения влияния выбора вида функций F,,

и F

, хорошо понятен инженерам и научным работникам. На самом деле

указанная «привычность» ведет к утверждениям типа «сверточный алго-

ритм предпочтительней алгоритма с разложением функции в ряд, посколь-

ку соответствующий математический аппарат более понятен». Однако, на

наш взгляд, эта причина популярности сверточного алгоритма не выдержи-

вает критики. Дело в том, что теория, положенная нами в основу метода

разложения в ряд, также «строга», как и теория, лежащая в основе свер-

точного и других алгоритмов реконструкции. Различные аспекты этой

проблемы легче всего пояснить при рассмотрении других теорий: и хотя

трудно объяснить поведение некоторых методов разложения в ряд на осно-

ве анализа Фурье, априорные знания легче учесть в методах разложения в

ряд,

чем в каком-либо другом преобразовании. К этому вопросу мы вер-

немся позднее.

В заключение отметим, что сверточный алгоритм приводит к эффектив-

ной реконструкции при сравнительно небольших затратах, и до тех пор,

пока мы не будем располагать сведениями об эффективном использовании

алгоритмов в других областях, наиболее приемлемым, по-видимому, будет

применение одного из имеющихся алгоритмов, предназначенных для рабо-

ты с параллельным пучком.

ПРИМЕЧАНИЯ И ССЫЛКИ

Математическая формулировка сверточного алгоритма для целей реконструкции

изображений при регистрации данных в параллельном пучке впервые была предло-

жена в [17]. В работе [135] был рассмотрен случай, учитывающий дискретный харак-

тер исходных данных. В обоих указанных подходах были использованы ограничен-

ные по пространственной частоте функции «окна», как это было подробно сделано в

доказательстве, предложенном в [78]. В работе [142] авторы предложили использо-

вать функции «окна» с пропусканием, отличным от равномерно ограниченного по

пространственной частоте; они были инициаторами применения функции «окна» в

виде sinx/x в сочетании с линейной интерполяцией. Термин «окно Хэмминга» был

введен в работе [31]. Как было показано в

[140],

в частности, использование функ-

ции обобщенного «окна» Хэмминга эквивалентно ограничению по пространственной

частоте исходных данных, сглаживаемых с помощью усреднения по трем точкам,

что обсуждалось, например, в работе

[142].

Исчерпывающий анализ функций «окна»

был проведен в

[140],

где впервые были корректно разделены сворачивающая и ин-

терполяционная функции. Приведенное выше изложение данного вопроса в значи-

тельной степени вызвано воздействием именно этой работы.

Понятие о семействе регуляризующих функций в литературу по реконструкции

изображений было введено в [77]. В настоящей книге был использован подход, пред-

ложенный в работе [29].

Точную формулировку теоремы о дифференцировании под знаком интеграла

можно найти в любом учебнике по математическому анализу, например в [8].

Общее содержание материалов, посвященных преобразованию Фурье, дискрети-

зации и интерполяции данных, легко можно найти в специальных монографиях по

упомянутым вопросам, например

книге [15]. Рассмотрение функции «окна» различ-

ного вида можно найти в литературе по обработке сигналов, например в книге

[130].

СВЕРТОЧНЫЙ АЛГОРИТМ РЕКОНСТРУКЦИИ 165

Примеры появляюшихся при использовании сверт очною алгоритма артефактов,

связанных с наличием в исходных данных высокочастотных компонент пространст-

венных частот, приведены в работе [83].

Имеется ряд публикаций, посвяшенных сравнению характернее ик свсрточного

алгоритма с алгоритмами, основанными на разложении в ряд [78, 142).

Другие алгоритмы реконструкции,

основанные на преобразованиях

для параллельного пучка

В данной главе обсуждаются два различных алгоритма реконструкции

по исходным данным, полученным в схеме с параллельным пучком, а

именно алгоритм Фурье и алгоритм, в котором сначала выполняют обрат-

ное проецирование, а затем фильтрацию данных в фурье-пространстве.

Оба упомянутых алгоритма основаны на использовании двумерного преоб-

разования Фурье, к рассмотрению которого мы и переходим.

9.1.

ДВУМЕРНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ

Двумерное преобразование Фурье представляет собой оператор, кото-

рый ставит в соответствие одну комплекснозначную

функцию

двух

поляр-

ных координат другой комплекснозначной функции ^у (также двух поляр-

ных координат) согласно определению

l&i Л

(Я,

Ф) = Г Г \г\ /(г, 0)ехр[ - InirR соз(Ф - ф)] dr

d<t>.

(9.1)

Двумерное

обратное преобразование

Фурье представляет собой опера-

тор,

который ставит в соответствие одну комплекснозначную функцию F

двух полярных координат другой комплекснозначной функции 3^ "^(так-

же двух полярных координат) согласно определению

1&г

П(г> Ф)

= f f

IRI

F(R, Ф)ехр[2я1Яг cos(tf> - Ф)] dR

d<b.

(9.2)

Jo J-oo

Для многих функций, в том числе и встречающихся в данной книге (в тех

случаях, когда это не оговорено особо), имеет место соотношение

= &

f = f. (9.3)

Аналогично тому, как мы поступали в одномерном случае [формула

(8.30)],

функцию / двух полярных координат можно разложить на гармонические

составляющие по двум переменным; двумерный фурье-образ при этом ха-

рактеризует сами гармоники. Поясним это более подробно.

Пусть /-=• функция двух полярных координат, a F—ее двумерный

ДРУГИЕ АЛГОРИТМЫ РЕКОНСТРУКЦИИ

167

фурье-образ.

Из

выражений

(9.2) и (9.3)

следует,

что

ас

R11

F(K, <D)|COS[2KK> соь(ф

- Ф) +

а(Я, Ф)]

d<£>

-со

|Я||Г(Я. Ф)|^п[2лЯ/

cos(<f)

- Ф) +

а(Я, Ф)1

ЛФ.

~ -ос

(9.4)

где а(/?, Ф)

—

аргумент функции

F(R

Ф). При

любых фиксированных зна-

чениях

R и

Ф функции вида IF(/?,

Ф)1 cos

[2тг/?г cos

(ф

—

Ф) + а(/?, Ф)] и

IF(/?,

Ф)1 sin

[2тгRr

cos

(ф

—

Ф) + а(/?, Ф)]

являются гармоническими

функциями двух полярных координат

(г, ф),

имеющими пространствен-

ную частоту

\R\

направление Ф, амплитуду IF(/?, Ф)I

начальную фазу

*(R,

Ф).

Как

же

выглядит гармоническая функция двух полярных координат?

За-

метим вначале,

что

если зафиксировать координату

ф, то

результирующая

функция достанется гармонической

теми

же

амплитудой

\F(R

Ф)1, на-

чальной фазой «(/?,

Ф) и

пространственной частотой

IR cos (ф

—

Ф)

Так,

на линии

проходящей через начало координат

образующей угол Ф

положительным направлением

оси х

(линия

ф = Ф),

упомянутая гармони-

ческая функция имеет пространственную частоту

IR I. На

любой линии,

перпендикулярной

L (т.е.

описываемой уравнением вида

cos (ф

—

Ф) = г

где

— константа), гармоническая функция двух полярных координат

по-

стоянна

(рис. 9.1).

Если функция

достаточно плавная, амплитуды гармоник

\F(R

Ф)1

на

высоких пространственных частотах

разложении

(9.4)

малы. Гово-

рят,

что

функция

ограничена

по

пространственной частоте, если

при

IRI

^ А/2

справедливо равенство [^У](/?,

Ф) = 0, где А —

положитель-

ное вещественное число, называемое шириной полосы пространственных

частот функции

(см. аналогичные определения

для

функции одной пере-

менной

разд.

8.4).

Весьма любопытны

полезны свойства двумерного фурье-образа, игра-

ющие важную роль

при

реконструкции изображений

нашедшие свое

вы-

ражение

в так

называемой теореме

проекциях. Последняя устанавливает

фундаментальное соотношение между преобразованием Радона, двумер-

ным преобразованием Фурье

оператором

представляющим собой

двумерный аналог одномерного преобразования Фурье, определямого сле-

дующим образом. Пусть

р —

функция двух переменных,

а р

описывается

соотношением (8.11)

виде

(() = p(f, 0);

тогда 3^

p — другая функция

двух переменных, определяемая соотношением

l^ypJL. fl) = l^PeJL). (9.5)

Другими словами, S?

представляет собой фурье-образ

по

первой перемен-

ной.