Хермен Г. Восстановление изображений по проекциям: Основы реконструктивной томографии

Подождите немного. Документ загружается.

128

ГЛАВА 7

ным у, где у

= pU,, 0

) для 1 < / = / (разд. 6.1 и 6.2). Мы ограничим

наше рассмотрение схемой сбора данных для М равномерно

распределенных в пространстве параллельных лучей в каждом ракурсе.

Пусть А обозначает угол между направлениями ракурсов (так что

А = гг/Л/), a d — шаг между параллельными лучами. Пусть Ш > Е > г.

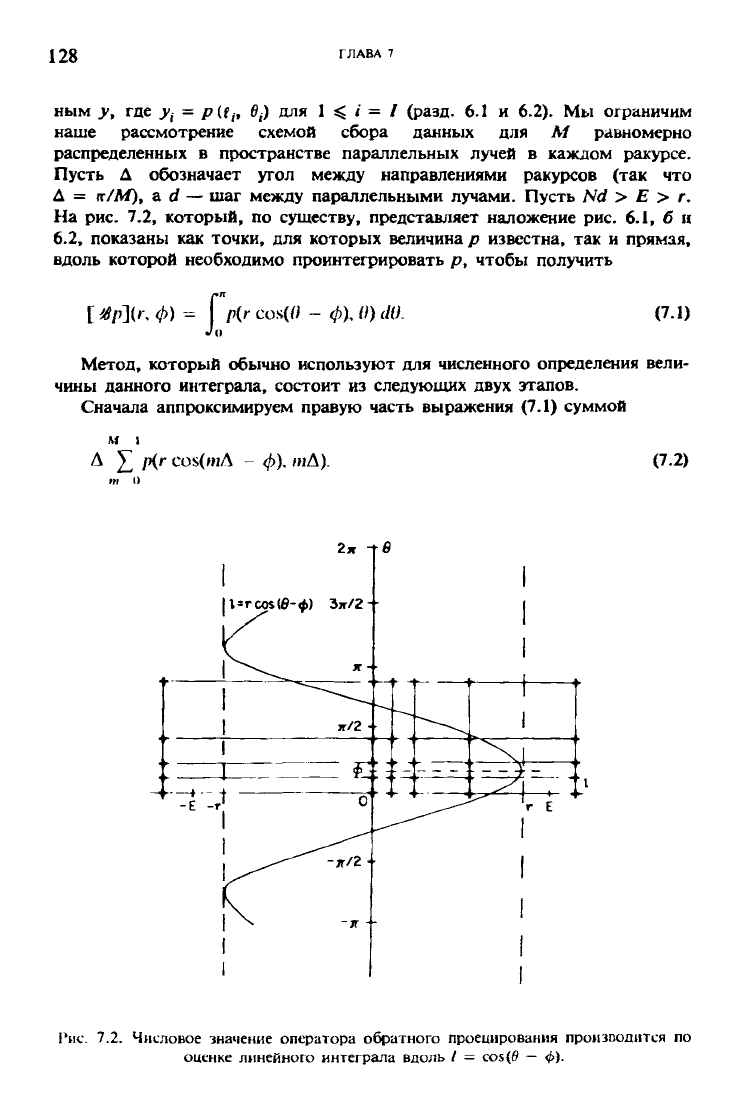
На рис. 7.2, который, по существу, представляет наложение рис. 6.1, б и

6.2, показаны как точки, для которых величина р известна, так и прямая,

вдоль которой необходимо проинтегрировать /?, чтобы получить

[Лр](г

ф)

-Г*

г cos(0 - </>), 0) dO.

(7.1)

Метод, который обычно используют для численного определения вели-

чины данного интеграла, состоит из следующих двух этапов.

Сначала аппроксимируем правую часть выражения (7.1) суммой

м 1

A YJ P(

COS(WIA - фУ #нА).

(7.2)

2я 10

Рис. 7.2.

Числовое значение оператора обратного проецирования производится

по

оценке линейного интеграла вдоль

/ =

cos(0

— ф).

АЛГОРИТМЫ ОБРАТНОГО ПРОЕЦИРОВАНИЯ

129

которую называют суммой

Римана

для данного интеграла, а затем произ-

водим оценку для каждого значения т величины р(гcos (тА

— Ф)>

тА) по

известным значениям

p(nd

тА) (

—

N ^ п ^ N) путем

интерполирования.

В реконструктивной томографии обычно используют два метода интер-

поляции: метод

интерполяции

по

ближайшему значению

и метод линей-

ной

интерполяции.

При интерполяции по ближайшему значению вычисля-

ют p(rcos(mA

—

ф), тА) по величинам p(nd, тА)

где п выбирают таким

образом, чтобы выражение \nd

—

rcos(mA

—

ф)\ имело наименьшее воз-

можное значение.

При линейной интерполяции п выбирают так, чтобы

nd ^ rcos(mA

—

ф) < (п + \)d, и вычисляют p(rcos(mА - ф), тА) по фор-

муле

(п +

1 )ii —

г cos(wA

—

ф)

, p(mi тА)

г cos(wA - ф) - nd

Р((п + IRiwA). (7.3)

Другими словами, определение

#p](r

ф) при помощи метода интерпо-

ляции по ближайшему значению выполняют следующим образом: склады-

вают вместе лучевые суммы для лучей по одному из каждого ракурса, ко-

торые являются ближайшими к точке (г, ф), и результат умножают на А.

Линейная интерполяция является несколько более сложной и дорогостоя-

щей:

вместо лучевых сумм одного луча складывают линейную интерполя-

цию лучевых сумм двух лучей, которые находятся по обеим сторонам от

точки (г, ф).

Чтобы получить дискретизированное изображение, вычисления повто-

ряют для центральной точки каждого элемента изображения и полученный

результат рассматривают как оценку плотности

данном элементе изобра-

жения. Такое дискретизированное изображение может быть представлено

как У-меоный вектор-столбец х* (разд. 6.3).

С учетом замечаний, сделанных в конце разд. 7.1, должно быть ясно,

что при таком методе можно получить дискретизированное изображение

х*

средние плотности которого

х*

существенно отличаются от средней

плотности х дискретизации х изображения, которое реконструируют. Так

как обычно мы имеем достаточно хорошую оценку х величины х, как это

отмечалось в конце разд. 6.4, то мы можем скорректировать это при по-

мощи нормировки, которая может быть либо

аддитивной,

либо

мульти-

пликативной.

Аддитивная нормировка позволяет получить дискретизированное изо-

бражение х**, у которого 7-компонента равна

*Г

л-Г + <v

.V*)./.

(7.4)

$ 0,22

0.21

0,20

0l9i

0,24

g 0,23

0,22-

0,21

0,20

0,19-

15 30 45 60 75 90 105 120

Координата

15 30 45 60 75 90 Ю5 120

Координате

Рис. 7.3.

Рис. 7.4.

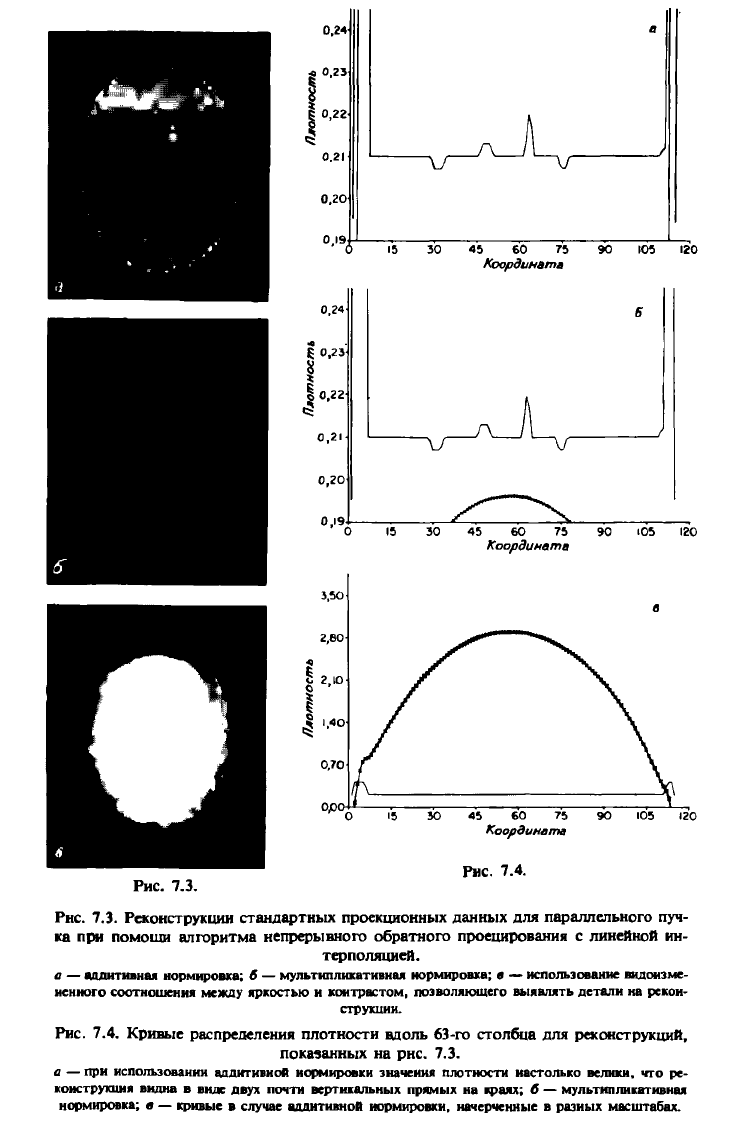
Рис. 7.3. Реконструкции стандартных проекционных данных для параллельного пуч-

ка при помоши алгоритма непрерывного обратного проецирования с линейной ин-

терполяцией.

—

аддитивная нормировка; б

—

мультипликативная нормировка; в

—

использование видоизме-

ненного соотношения между яркостью и контрастом, позволяющего выявлять детали на рекон-

струкции.

Рис. 7.4. Кривые распределения плотности вдоль 63-го столбца для реконструкций,

показанных на рнс. 7.3.

—

при использовании аддитивной нормировки значения плотности настолько велики, что ре-

конструкция видна в виде двух почти вертикальных прямых на краях; б

—

мультипликативная

нормировка; в — кривые в случае аддитивной нормировки, начерченные в разных масштабах.

АЛГОРИТМЫ ОБРАТНОГО ПРОЕЦИРОВАНИЯ

131

Мультипликативная нормировка дает дискретизированное изображение,

у-я компонента которого равна

х;* = х?(х/3с*). <7.5)

Последнее выражение применимо только тогда, когда х* Ф 0. Отме-

тим,

что в любом случае средняя плотность *•• равна х.

Интересное свойство мультипликативной нормировки состоит в том,

что при ее проведении результат_получает вновь правильную размерность.

Это связано с тем, что величина х имеет размерность обратной длины, так

как получается суммированием с безразмерной величиной, деленной на сум-

му длин, в результате чего xj

имеет правильную размерность. С другой

стороны (7.4) почти не имеет физического смысла: величинах

—

х* равна

разнице между величиной, имеющей размерность обратной длины (х), и

безразмерной величины (*• ). По этой причине обычно рекомендуют

пользоваться мультипликативной, а не аддитивной нормировкой.

Методы, описанные выше, были использованы для стандартных проек-

ционных данных в параллельном пучке с применением метода линейной ин-

терполяции. Полученные результаты представлены на рис. 7.3, а соот-

ветствующие кривые распределения плотности вдоль столбца 63 — на рис.

7.4. Как видно из данных по столбцу, рассмотренные алгоритмы не приме-

нимы для исследования тканей внутри головы. Изображение на рис. 7.3, б

выглядит черным. Это связано с принятым нами условием воспроизводить

значения 0,1945 см

-1

и меньше черным цветом (разд. 4.3). По этой причине

мы воспроизводим данное изображение при другой установке соотношения

между яркостью и контрастом на рис. 7.3, е. Меры различия между изо-

бражениями приведены в табл. 7.1.

Таблица

7.1

Меры различия между изображениями и время счета на ЭВМ при «непрерывном»

обратном проецировании реконструкций по стандартным проекционным данным

для параллельного пучка

Алгоритм нормировки

Аддитивный

Мультипликативный

14,6040

0,8111

12,0195

0,5818

3,9950

0,2731

125

7.3.

ДИСКРЕТНОЕ ОБРАТНОЕ ПРОЕЦИРОВАНИЕ

В последнем разделе мы получили дискретизированное изображение пу-

тем численного определения интеграла в выражении (7.1) для центральных

132

ГЛАВА 7

точек элементов изображения. В качестве альтернативного подхода можно

использовать алгоритм с разложением функции в ряд.

Рассмотрим базисные изображения, которые имеют значения 1 внутри

элемента изображения и 0 вне [базисные изображения определены выраже-

нием

(6.17)].

В этом случае г

/у

равна вычисленной длине пересечения /-го

луча с у-м элементом изображения. Приведенные ниже критерии описыва-

ют то, что следует ожидать из интуитивных соображений от реализации

алгоритма обратного проецирования для элементов изображения:

а) луч должен давать вклад только в те элементы изображения, кото-

рые он пересекает, и не давать вклада в остальные;

б) вклад /-луча в элемент изображения должен быть пропорционален

— измеренной лучевой сумме для /-го луча;

в) вклад /-го луча ву-й элемент изображения должен быть пропорциона-

лен г-.

Все эти критерии удовлетворяются, если мы используем для оценки

плотности в

x*j

в у-м элементе изображения выражение

1 - I'YjJV (7.6)

В матричном представлении это выражение можно записать следую-

щим образом:

v* = Я

\\ (7.7)

где R

— транспонированная матрица /?, т.е. матрица, у которой (/, у>й

элемент равен г-

{

. Подробно реализация будет описана в разд. 11.1.

Соотношения, приведенные выше, не зависят от того, какие базисные

функции приписаны элементам изображения. Мы полагаем в общем слу-

чае,

что выражение (7.7) является решением дискретной реконструкционной

задачи при использовании алгоритма обратного проецирования для задан-

ной проекционной матрицы R. В частности, мы называем результат умно-

жения /-мерного вектора на R

дискретной обратной проекцией.

Точно так же, как и в случае алгоритма непрерывного обратного прое-

цирования, средняя плотность х* может существенно отличаться от сред-

ней плотности в изображении, подлежащем реконструкции. В таком случае

можно получить хороший результат, применяя аддитивную и мультипли-

кативную нормировку [см. (7.4) и

(7.5)].

Это, конечно, имеет смысл, если

разложение в ряд представляет со^ой дискретизированное выражение.

Дискретное обратное проецироание, определяемое выражением (7.7),

можно использовать для любой схемы сбора данных. Для стандартных

проекционных данных в параллельном пучке это приводит к результату,

весьма сходному по внешнему виду с тем, что показано на рис. 7.3. В том

случае, когда дискретное обратное проецирование применяется для стан-

дартных проекционных данных для веерного пучка, получают несколько

0,24-

£0,23

0,20

0,19 +

0,24 '

10,23-1

§0,22

0,21-(|

0,20

0.19

15 30 45 60 75 90 105 120

Координата

. лН\

15 30 45 60 75 90 105 120

Координата

\2Ъ0

'i/^^^vv^'^

^ 6,401

VV^y^AAl^

15 30 45 60 75 90 105 120

Координате

РИС.

7.5.

Рис 7.6.

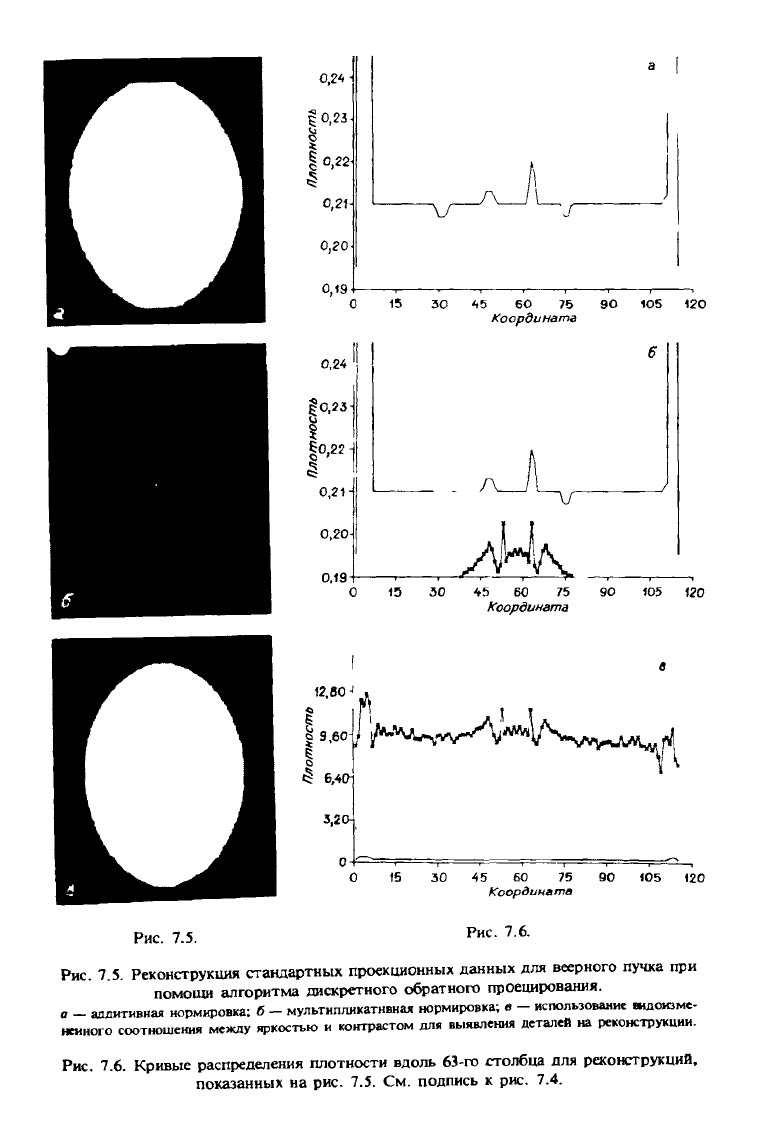
Рис. 7.5. Реконструкция стандартных проекционных данных для веерного пучка при

помощи алгоритма дискретного обратного проецирования.

a - аддитивная нормировка; б - мультипликативная нормировка; в - использование видоиэме-

неиного соотношения между яркостью и контрастом для выявления деталей на реконструкции.

Рис. 7.6. Кривые распределения плотности вдоль 63-го столбца для реконструкций,

показанных на рис. 7.5. См. подпись к рис. 7.4.

134

ГЛАВА 7

Таблица

7.2

Меры различия между изображениями и время счета на ЭВМ для реконструкций

дискретного обратного проецирования по стандартным проекционным данным для

веерного пучка

Алгоритм нормировки

d г

Аддитивный

Мультипликативный

80,5233

0,8109

66,8735

0,5818

25,2084

0,2727

295

297

отличные с виду результаты, которые приведены на рис. 7.5. Кривая рас-

пределения плотности вдоль столбца 63 этих реконструкций дана на рис.

7.6. Другие подробности, характеризующие алгоритм обратного проециро-

вания, приведены в табл. 7.2.

ПРИМЕЧАНИЯ И ССЫЛКИ

Алгоритм обратного проецирования в различных аналоговых и цифровых реа-

лизациях был предложен рядов авторов. Историю этого вопроса можно найти в ра-

боте [51]. В частности, прием, описанный в разд. 7.2, взят из работы [98].

Численное определение интегралов и особенно сумм Римана достаточно подроб-

но изложено в [37]. Рассмотрение других возможных алгоритмов численного опреде-

ления интегралов из (7.1) проведено в работе [21].

Другие алгоритмы интерполяции, отличные от тех, которые были рассмотрены

выше, изучались рядом авторов применительно к алгоритму обратного проецирова-

ния.

Оценка интерполяционных методов Лагранжа приведена в работе

[140].

Оппен-

гсйм [125] предложил использовать модифицированные кубические сплайны; эта те-

ма была далее рассмотрена в работе [86]. Метод фурье-интерполяции обсуждается в

работе

[156].

Оператор обратного проецирования для геометрии с веерным пучком (третья и

четвертая схемы сканирования, рис. 3.3, в иг) приводится в работе [55].

Сверточный алгоритм реконструкции

для параллельного пучка

Благодаря простоте своей реализации

высокой точности вычислений

сверточный алгоритм реконструкции нашел наибольшее применение

в ре-

конструктивной томографии

для

параллельного пучка. Сверточный алго-

ритм представляет собой преобразование,

котором дифференцирование

преобразование Гильберта заменены одной операцией свертки.

8.1.

СВЕРТКА, ПРЕОБРАЗОВАНИЕ ГИЛЬБЕРТА, РЕГУЛЯРИЗАЦИЯ

Сверткой двух заданных функций

ф вещественного переменного

на-

зывается функция (также вещественного переменного)

ф * ф,

определяемая

соотношением

гас

[ф * ФШ = ф(иШь - и) du. (8.1)

J-oo

Заметим,

что при

некоторых значениях параметра

свертка

[ф *

ф]&)

не

определена, поскольку интеграл

правой части

(8.1)

может

не

существо-

вать, однако, согласно сказанному выше, считаем,

что

свертка

[ф *

ф]{и)

определена всюду,

где это

необходимо.

Отметим также,

что

свертка представляет собой оператор, который,

воздействуя

на две

функции

ф и ф

образует новую функцию

ф ♦ ф. Не-

трудно показать,

что

ф+ф=ф*фв

том

смысле,

что для

всех значений

v имеет место равенство вида

W*№) =

W**M

(8.2)

Мы

уже

рассматривали пример свертки,

именно: преобразование

Гильберта

<Я£ф

функции

можно определить

как

свертку

функцией

вида

р(и)= -(\/пи) (8.3)

Другими словами, можно записать выражение

Жф

= ф* р, (8.4)

причем функция

определена формулой (8.3). Комбинируя соотношения

136

ГЛАВА

(8.1),

(8.3) и

(8.4), получим

<Ми)

[Жф]&)

= - - Щ±

du.

(8.5)

7Г

J.^ V - U

Выражение

правой части (8.5) представляет собой

так

называемый не-

собственный интеграл как первого,

так и

второго рода. Интегралом пер-

вого рода последний считается потому,

что

пределы интегрирования

в нем

бесконечны

(от

—

а>

до оо),

однако

при

реконструкции изображения

это не

должно смущать

нас,

поскольку значения функции ф[и) обращаются

нуль

вне конечной области,

что

можно видеть

из

сравнения выражений

(8.5) и

(6.12).

Видно также,

что при

реконструкции изображения преобразование

Гильберта выполняется

для

функции ф(и)

= q(u, в) при

фиксированном

значении

в и при М ^ £,

причем

ф(и) = q(u, в) =

р](ы,

в) = [®уМП(и, в) = 0 (8-6)

[формулы (6.6), (6.11), (6.12)1.

Интеграл

правой части выражения

(8.5)

является также несобствен-

ным интегралом второго рода, поскольку

при и = v

подынтегральное вы-

ражение расходится. Здесь

мы

будем понимать интеграл (8.5)

смысле

его

главного значения,

т.е.

тм=-

ш\Г^

)

и+

Г «»±А

л,

ГСе-0

U-ao V ~ U J

V + E

V - U )

Даже если указанный интеграл

существует, вычислить

его

далеко

не так

просто. Одним

из

методов

его

вычисления является метод регуляризации,

который предполагает определение множества \Р

> 0)

функций

ве-

щественного переменного

(где

индекс

А —

положительное вещественное

число).

Идея

по

существу состоит

в том, что

функцию

для

интересую-

щей

нас

функции

подбирают такой, чтобы выполнялось равенство вида

lim

ф* р

= %

ф,.

(8.8)

i4-»oo

Тогда для произвольного фиксированного значения

вычисление свертки

левой части выражения

(8.8)

производится достаточно просто.

Для более точного выбора функции

необходимо определить класс

функций,

для

которого справедливо равенство (8.8).

разд.

16.7

точно

определен смысл утверждения

о том, что

функция

достаточно «хоро-

шая»

точке i>,

пока мы просто можем считать ф «хорошей»

во

всех точ-

ках. Множество Jp^

1>1

> 0)

функций назовем семейством регуляризую-

щих функций, если

для

любой функции ф вещественного переменного

и лю-

бого вещественного значения

v, при

котором

достаточно «хорошая»,

справедливо соотношение

СВЕРТОЧНЫЙ

АЛГОРИТМ РЕКОНСТРУКЦИИ

137

Таблица

8.1

Определения

часто используемых функций «окна»

Название

функции «окна»

(V)

Прямоугольный

импульс, ограниченный

по

полосе частот

Косинусная

Синусная

Обобщенная

функция Хэмминга

параметром а (0,5 < а ^ 1)

cos(*C/A4)

sin{*U/A)/{Tcu/A)

а + (1 - а)

COS(1TU/A)

> При а = 0,5 функцию обобщенного «окна» Хэмминга называют хэннинго-

вым «окном». При а = 0,54 эту же функцию называют «окном» Хэмминга.

-о,«о

-0,20 0,00

Частот*

0,20 0,40

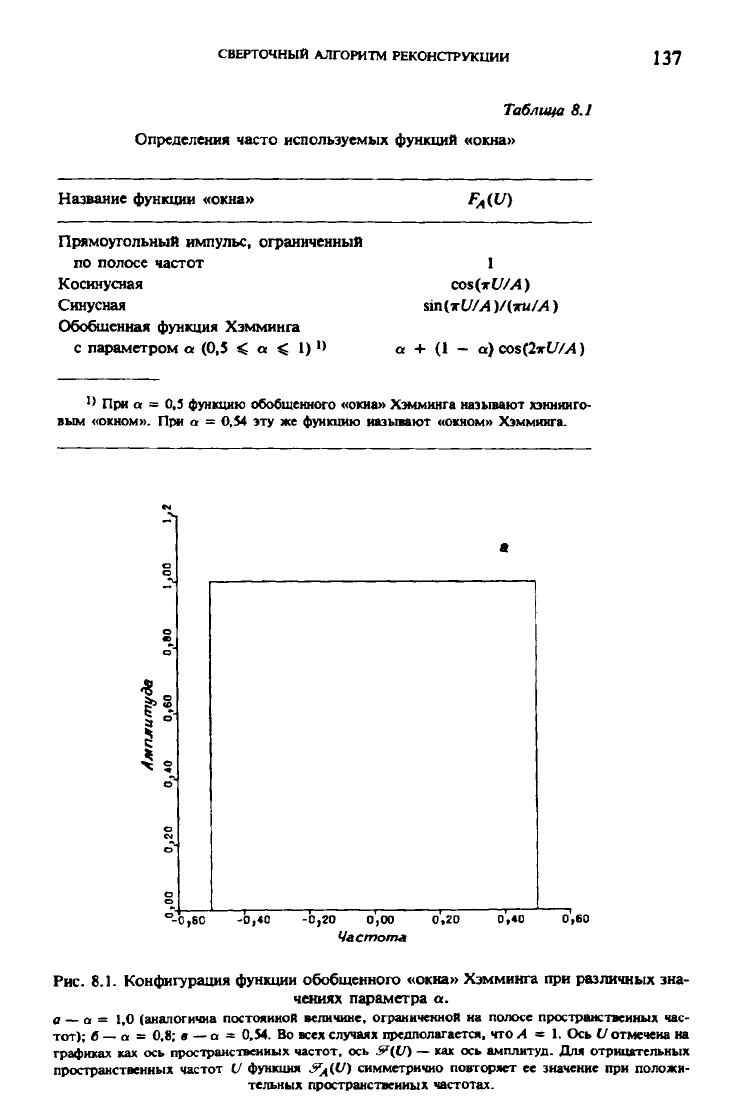
Рис.

8.1. Конфигурация функции обобщенного «окна» Хэмминга при различных зна-

чениях

параметра о.

a _ a

—

1,0 (аналогична постоянной величине, ограниченной на полосе пространственных час-

тот);

б — a = 0,8; в — a = 0,54. Во всех случаях предполагается, что А = 1. Ось (/отмечена на

графиках как ось пространственных частот, ось &{JU) — как ось амплитуд. Для отрицательных

пространственных частот V функция ^((/) симметрично повторяет ее значение при положи-

тельных пространственных частотах.