Хермен Г. Восстановление изображений по проекциям: Основы реконструктивной томографии

Подождите немного. Документ загружается.

148

ГЛАВА 8

ного переменного

другой комплекснозначной функцией (также веществен-

ного переменного), определяемой

как

[^'

0](м)=

<£(C/)exp[2rciC/w]

dU.

(8.28)

J -00

Наиболее важное свойство упомянутых операторов состоит

том,

что для

многих функций

(в том

числе

по

предположению

и для

всех используемых

в данной книге) имеет место соотношение

&ф = &&-

ф = ф.

(8.29)

Именно поэтому оператор

называется обратным преобразованием

Фурье.

Чтобы дать простое качественное объяснение соотношениям между

функциями

и их

фурье-образами, необходимо сделать небольшое отступ-

ление.

Гармонической функцией называют функцию, которую можно предста-

вить либо как

cos(2nUu

+ а),

либо

как

sin(2irC/u

+ а), где R

С/

а —

постоянные,

а и —

переменная. Амплитудой такой функции называют

ве-

личину

\R\ (т.е. все

значения функции лежат

промежутке

от —

до +/?).

Говорят также,

что

функция периодична

периодом 1/1

С/1,

если

для

всех

U выполняется условие

cos(27rC/(u

1/1

С/1

+ а) = R

COS(2TTC/M

+ а).

Форма гармонической функции только

на

одном периоде приведена

на

рис.

7.2.

Поскольку

на

единичном интервале укладывается

С/1

полных периодов

функции,

то U

называют частотой,

величину

а —

начальной фазой коле-

баний.

Чтобы наглядно ощутить качественные связи между функцией

и ее

фурье-образом, предположим,

что

/•оо

<£(")= \<b(U)\cos(2nUu + a(U))dU

"- 00

/•СО

+ i\

\<SKU)\sm(2nUu

+ cx(U))dU,

(8.30)

J -

где

OL(V)

— аргумент функции Ф(С/). Данное соотношение легко доказыва-

ется

помощью формул (8.29), (8.28)

(8.26). Заметим,

что для

любого

фиксированного значения

С/

подынтегральные выражения

правой части

выражения (8.30) представляют собой гармонические функции

по

перемен-

ной

I/,

изменяющиеся

частотой

С/,

амплитудой, пропорциональной моду-

лю фурье-образа Ф(С/),

начальной фазой, совпадающей

аргументом

Ф(С/). Грубо говоря, соотношение (8.30) гласит,

что

как

вещественную,

так

и мнимую часть функции

можно разложить

по

частотам

на

гармониче-

ские составляющие,

амплитуда

начальная фаза

той или

иной гармоники

СВЕРТОЧНЫЙ АЛГОРИТМ РЕКОНСТРУКЦИИ

149

с частотой

U в

таком разложении определяются величиной фурье-образа

функции

ф в

точке

Разумно предположить,

что для

медленно меняющихся функций менее

важен вклад, даваемый высокочастотными компонентами спектра,

т.е. для

гладких функций

величина [Уф](и) достаточно мала

на

высоких часто-

тах. Данное выражение можно доказать строго математически, однако

это

не входит

круг рассматриваемых

данной книге вопросов.

Тем не

менее

внимания заслуживает

так

называемая ограниченная

по

частоте функция

для

которой [&ф]{и)

= 0

при

А/2. В

этом случае говорят,

что

функция

имеет полосу частот

А.

Функции,

которыми

мы,

вероятно,

будем иметь дело при реконструкции изображений,

не

являются ограничен-

ными

по

частоте, однако всегда существует некая ограниченная

по

частоте

функция, практически

не

отличающаяся

от

реально существующей.

Нами

уже

были рассмотрены некоторые ограниченные

по

частоте функ-

ции;

частности, согласно определению (8.21), ограниченной является сво-

рачивающая функция ядра

Чтобы доказать

это,

положим

4U)=W\F

(\U\l

(8.31)

Заметим,

что

Ф({/)

при

\U\

/1/2,

также имеет место свойство чет-

ности

Ф(—

Ф(£/). Используя

эти

соотношения

для Ф({/) и

подставляя

их

формулу (8.28), получим

гА/2

[&-

Щ(и)

= 2

<t>(U)cos(27iUu)

dU.

(8.32)

Сравнение приведенной формулы

формулы (8.21) показывает,

что д(и)

\&~

Ф](к)>

поэтому

является функцией

Ф,

определяемой соотно-

шением (8.31). Последнее означает,

что

сворачивающая функция

виде

функции «окна» шириной

ограничена

по

частоте этой

же

величиной.

Теперь естественным образом возникает следующее построение. Функ-

ции

были введены

разд.

8.1,

соотношения (8.10) привели

нас к се-

мейству

[р

\А

регуляриэирующих функций. Цель построения данно-

го семейства состоит

аппроксимации гильберт-образа [формула

(8.9)],

ко-

торую можно осуществить

наперед заданной точностью

любой точке

при достаточно большом значении

А.

Значение функций

произволь-

ной точке при увеличении

стремится к единице.

связи

этим возникает

вопрос: почему

бы не

использовать взамен выражения (8.31)

его

предель-

ное значение,

именно

не

положить

Ф(С/)

It/I? Если сделать

это, то,

естественно,

мы

получим соотношение вида

Я(р *

Ф); (8.33)

т.е.

при

этом

мы

заменяем приближенную формулу (8.19)

на

формулу,

по-

зволяющую вычислить величину

точно.

этих рассуждениях име-

ется существенный изъян: если функция

определяется соотношением

150

ГЛАВА 8

Ф(С/)

= It/I, то

обратное преобразование Фурье

не

определено

том смысле,

что

интеграл

бесконечными пределами интегрирования

правой части определения

для

обратного преобразования Фурье (8.28)

не

существует.

Таким образом, указанный прием оказывается обреченным

на

неудачу,

а проблема выбора функции

по-прежнему остается открытой. Стремле-

ние достаточно точно аппроксимировать гильберт-образ

очевидностью

требует выбора значения

достаточно большим, однако,

как это

будет

показано ниже, структура используемых данных может диктовать проти-

воположное.

Теперь напомним обозначения, использованные

разд.

8.2.

Функция

двух переменных,

для

которой необходимо вычислить обратное преобразо-

вание Радона, обозначалась буквой р.

Для

любого угла

функция

опре-

делялась

из

соотношения (8.11).

На

этом этапе производится свертка функ-

ций

</-для каждого значения

[формула

(8.18)].

Для пояснения способа

выборки функции

рассмотрим вопрос

о том,

когда свертка функций

q приводит

фурье-образу

от

Важным соотношением, имеющим непосредственное отношение

рас-

сматриваемому вопросу, является теорема свертки, утверждающая,

что

фурье-образ свертки двух функций равен произведению фурье-образов этих

функций,

или в

операторной записи

ФШ) =

l?<t>]W)

х ОТ](С/). (8.34)

Применяя данную теорему

рассмотренному выше случаю, получим

ШГе * qJ](U) = \U\F

(\U\)lf

](Uy

(8.35)

откуда видно,

что

величина фурье-образа свертки

* q в

точке

превы-

шает величину фурье-образа функции

в той же

точке

\U\F

(\U\)

раз.

Этот вывод имеет много интересных следствий. Например, свертка р

* q

является ограниченной

по

частоте функцией

шириной полосы

А. Так как

практический интерес связан

не с

формулой аппроксимации обратного пре-

образования Радона (8.19),

а с его

реальным применением

разд.

8.3, то

необходимо рассмотреть дискретные формы записи свертки

операторов

преобразования Фурье.

8.5. ДИСКРЕТИЗАЦИЯ

ИНТЕРПОЛЯЦИЯ

С помощью соотношения (8.19)

мы

определили оценку/*, получаемую

в результате математически идеализированного сверточного алгоритма,

как обратное проецирование р*

где

р —

функция двух переменных,

об-

ратное преобразование Радона которой необходимо найти,

a q —

сворачи-

вающая функция.

разд.

8.3

отмечалось,

что

операция обратного проеци-

рования обычно применяется

не к

свертке р*

а к ее

аппроксимирован-

ному значению, которое обозначалось через р

. Чтобы использовать

это

СВЕРТОЧНЫЙ АЛГОРИТМ РЕКОНСТРУКЦИИ

151

аппроксимированное значение [формула

(7.2)],

необходимо, чтобы функция

{

(. 0) была известна для тех величин ( и 0, которые определяются из

соотношений ( = г со$(/иД - ^) и б = тД. Так как точка с координатами

(г,

<£), в которой необходимо вычислить интенсивность изображения, мо-

жет находиться в любой точке поля изображения, то функцию р

необходи-

мо определять во всех точках ( е, 0), причем — £ < t ^ £ и 0 = тА, где

т — целое число, лежащее в интервале 0 ^ т ^ М - 1. Определение

функции р

в указанных точках производят в два приема. Вначале по фор-

муле (8.23) мы определяем точные значения р

в точках (n'd

/иД), где

п'

— целое число (—N ^ п' < Л/), а затем показываем, что р

(г соь(тй

—

ф), тА) получают путем интерполяции из значений p

(n'd, тв). В дан-

ном разделе рассмотрим соотношения между сверткой

и ее аппрок-

симированным значением р

Отметим прежде всего, что указанное рассмотрение относится только к

функциям одного переменного, так как для любого фиксированного значе-

ния /иД величина р

( i

/иД) определена значениями функции р( (, тД), т.е.

значениями р

тА

( е ) [формула (8.11)J. Таким образом, эту проблему можно

переформулировать следующим образом.

Предположим, что р

— функция одной вещественной переменной, при-

чем р

( i ) = О при I ( I ^ £, а Е — положительное вещественное число.

Пусть д является другой функцией, также одной переменной, d — вещест-

венное число, а N — целое число, такое, что Nd > Е. Определим некото-

рую новую функцию t таким образом, чтобы для целых значений п' вы-

полнялось равенство

t(rid) = d X Pe(nd)ci((n - n)d). (8.36)

Для всех значений вещественной переменной функция /(f) определя-

ется путем интерполяции значений t(n'd).

Упражнение. Исследуйте вопрос о том, каким образом выбор функции

q и метода интерполяции сказывается на соотношениях, связывающих

функции р

и t.

Здесь мы изложим постановку задачи в частной формулировке, потому

что р

представляет собой проекционные данные, которые поступают с ре-

ального прибора. С другой стороны, выбор сворачивающей функции и ал-

горитма интерполяции делаем мы сами, и о том, как их выбрать, показано

ниже.

Для решения указанной проблемы более подробно рассмотрим сущ-

ность процесса интерполяции. Для любого положительного вещественного

числа d (называемого шагом дискретизации) и любой функции веществен-

ных переменных (называемой интерполяционной функцией) определим опе-

ратор J/g, который назовем оператором интерполяции для шага дискре-

тизации d и для интерполяционной функции ф и который связывает произ-

вольную функцию ф одной вещественной переменной с другой функцией

152

ГЛАВА 8

■^~/ф

(также одной вещественной переменной) согласно соотношению

\J*A1(v)= £ <Kndmv-nd).

(8.37)

П= ~ ас

В практических расчетах сумма

выражении (8.37) обычно имеет конеч-

ное число слагаемых, поскольку

большинстве приложений интерполяци-

онные функции полагают равными нулю

вне

некоторого небольшого

ин-

тервала. Например,

при

интерполяции

по

двум ближайшим значениям

ис-

пользуют функцию

>р

следующего вида:

ФМ =

(1 если

- d/2 < и < d/2,

0.5 если

\и\ = d/2,

(8.38)

0 если

> d/2

Здесь предполагаем,

что

усредненное значение желательно получить

точ-

ке,

находящейся точно посредине между двумя точками отсчета.

При ли-

нейной интерполяции необходимо использовать интерполяционную функ-

цию

(

другого вида,

именно

«-{;-"<

, i х

• ~~ \

/d\

если

\и\ < d,

ФАи)

39)

если

|и| > d.

Заметим,

что для

каждой

из

двух указанных выше интерполяционных

функций справедливо соотношение

№Ф](т1) =

<Knd\

(8.40)

для любой функции

ф и при

любом целом значении

п.

Интерполяционные

функции, удовлетворяющие соотношению (8.40), будем называть собствен-

ными интерполяционными функциями,

Предположим,

что

функция

/ в

нашем случае должна задаваться

с по-

мощью собственной интерполяционной функции

ф.

Точный метод опреде-

ления функции состоит

следующем:

по

формуле (8.36) определяют функ-

цию

t в

точках

координатами

n'd

для всех целых значений

л',

затем

с по-

мощью соотношения (8.37)

при

замене ф

на / для

всех вещественных значе-

ний

определяют функцию

—

^t. При

этом фурье-образ функции

можно найти следующим образом.

Пусть имеем

•Fi(V)= £ lfp

HU + k/d).

(8.41)

к- -СС

FzW) = Е l?<lHU + k/d),

(8-42)

СВЕРТОЧНЫЙ АЛГОРИТМ РЕКОНСТРУКЦИИ

153

F>(U)

= WKU)/d.

(8.43)

тогда получаем

[•*>]«/)

= F

{

(U) х F

(U) х F,(U).

(8.44)

Доказательство данного утверждения требует более серьезной матема-

тической подготовки,

чем та,

которая предполагалась

при

написании этой

книги, хотя этапы доказательств имеют важные приложения

сверточном

методе.

следующем разделе речь пойдет

выборе сворачивающей

и ин-

терполяционной функций, базирующемся исключительно

на

соотношениях

(8.41)

—

(8.44).

8.6. ВЫБОР СВОРАЧИВАЮЩЕЙ И ИНТЕРПОЛЯЦИОННОЙ ФУНКЦИЙ

Как

уже

указывалось, соотношения (8.41)

—

(8.44) дают

нам

возмож-

ность производить выбор сворачивающей

q и

интерполяционной

функ-

ций. Предполагается,

что

функция

аппроксимирует свертку

* q. Со-

гласно теореме свертки (разд.

8.4),

фурье-образ свертки

* q

равен про-

изведению фурье-образов функций

и q. С

другой стороны, фурье-образ

функции

/ в

выражении (8.44) представлен произведением следующих трех

функций: функции F

(U)

зависящей

от

проекций

;

функции F

(U)

завися-

щей

от

вида сворачивающей функции

наконец, функции F

{U)

зависящей

от интерполяционной функции

ф.

Грубо говоря,

мы

отождествляем функ-

цию

Fj с

функцией

^р

—

c &q

функции

ставим

соответствие

функцию, величина которой всегда порядка единицы. Взаимная связь меж-

ду упомянутыми тремя парами функций также важна, особенно

связи

тем,

что

поставленная задача оказывается практически неосуществимой.

Рассмотрим функции

{

, F

и F

по

отдельности.

Фигурирующая

выражении (8.41) функция

является периодической

функцией

периодом

\/d.

(Напомним,

что d

— шаг дискретизации

по

пере-

менной

е, или,

другими словами, расстояние между параллельными луча-

ми,

вдоль которых ведут измерение лучевых сумм). Если проекционные

данные изменяются достаточно медленно

пределах области дискретиза-

ции,

то

можно считать,

что

значения \[^p

](U)\ достаточно малы

при

U\ > \/2d

(другими словами, считаются малыми амплитуды высокочас-

тотных гармоник функций

фурье-образе функции

Тогда

при

\U\ < l/2d

получаем соотношение вида

(U) ^ 1?

Рв

]{и\

(8.45)

которое позволяет идентифицировать функции

F, и

&р

* Однако очевидно,

что соотношение (8.45)

не

имеет силы

при U > l/2d,

поскольку функция F

вне интервала

—

l/2d ^ U < l/2d

просто периодически повторяет значе-

ния,

которые

она

принимала

на

самом интервале. Между

тем

фурье-образ

^р

от

проекции

этим свойством

не

обладает. Отсюда следует,

что ее-

154

ГЛАВА 8

_| 1 , 1 , ц-

0 1,5 3,0 4,5 6fi 7.5

Рис. 8.4. Эффект возникновения ложных спектральных составляющих.

Периодическая функция с периодом 2 или с пространственной частотой 1/2 (вверху) выбирается с

интервалом выборки 1,5. Интерполяция по ближайшим значениям дает функцию с периодом 6,

•

или с частотой 1/6 (внизу).

ли функцию F

{U) можно использовать для аппроксимации фурье-образа в

интервале

-1/2*/

< U < 1/2*/, то вне указанного интервала этого делать

нельзя. Если мы предположим, что функция достаточно медленно изменя-

ется в пределах интервала дискретизации, то разумной аппроксимацией

[&p

](U) при \U\ > 1/2*/ будет нулевое значение.

Весьма важным моментом при рассмотрении является следующий воп-

рос:

если значения фурье-образа [&p

](U) представляются малоинформа-

тивными при значениях It/1 ^ 1/2*/, то при этом возникают серьезные

трудности, поскольку у нас отсутствует метод аппроксимации фурье-

образа

при больших значениях

U\. Более того, выражение (8.45) не

имеет силы даже в интервале - 1/2*/ < U < \/2d

в чем можно убедиться

из сравнения определения F

{

(U) (8.41) и выражения (8.45), поскольку при

к Ф

величины [&p

](U + k/d) отбрасывать нельзя. Таким образом, ам-

плитуды высокочастотных компонент спектра р

при малых значениях

С/1

влияют на величину F

(U). В результате возникают ложные частоты, пока-

занные на рис. 8.4.

Явление возникновения ложных частот состоит в следующем: если мы

производим выборку функции р

недостаточно подробно, то при этом те-

ряется не только информация о высокочастотных компонентах в спектре

исходных данных, но и искажаются его низкочастотные компоненты.

Априорная информация (разд. 6.4) в этом случае может помочь восстано-

вить утраченную информацию, однако в сверточном алгоритме использо-

вать подобную информацию невозможно. Если мы не можем вести выбор-

ку чаще (конструкция аппарата обычно ограничивает ее частоту), мы

должны смириться с тем, что реконструированнное изображение будет

низкого качества, если проекции содержат интенсивные высокочастотные

компоненты спектра.

Безусловно, представляется маловероятным, чтобы амплитудные вари-

ации имели бы граничную частоту, в точности равную 1/2*/. Уже отмеча-

лось,

что амплитуды гармоник на пространственных частотах, немного

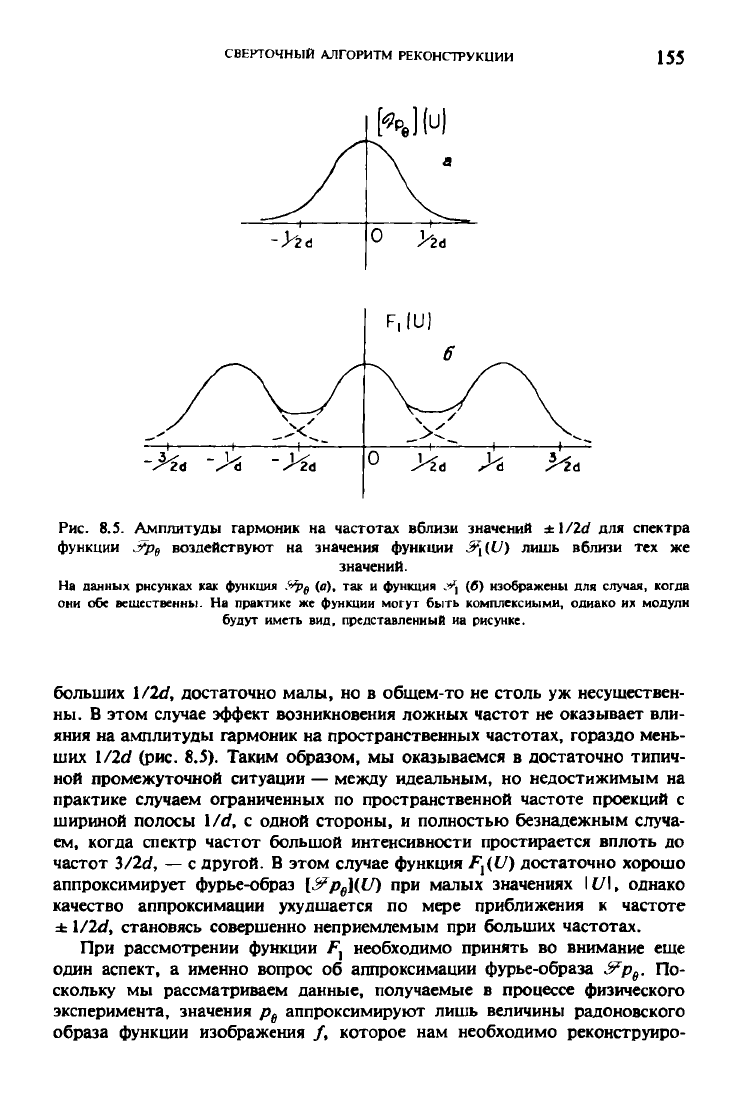
СВЕРТОЧНЫЙ АЛГОРИТМ РЕКОНСТРУКЦИИ

155

-Уг* -У* -Угл

Рис. 8.5. Амплитуды гармоник на частотах вблизи значений ±\/2d для спектра

функции г?р

воздействуют на значения функции £\(U) лишь вблизи тех же

значений.

На данных рнсунках как функция :-ф

(о), так и функция У

(б) изображены для случая, когда

они обе вещественны. На практике же функции могут быть комплексными, однако их модули

будут иметь вид, представленный иа рисунке.

больших l/2d, достаточно малы, но в общем-то не столь уж несуществен-

ны.

В этом случае эффект возникновения ложных частот не оказывает вли-

яния на амплитуды гармоник на пространственных частотах, гораздо мень-

ших l/2d (рис. 8.5). Таким образом, мы оказываемся в достаточно типич-

ной промежуточной ситуации — между идеальным, но недостижимым на

практике случаем ограниченных по пространственной частоте проекций с

шириной полосы \/d, с одной стороны, и полностью безнадежным случа-

ем,

когда спектр частот большой интенсивности простирается вплоть до

частот 3/2d, — с другой. В этом случае функция F

(U) достаточно хорошо

аппроксимирует фурье-образ l&p

](U) при малых значениях It/I, однако

качество аппроксимации ухудшается по мере приближения к частоте

± \/2d

становясь совершенно неприемлемым при больших частотах.

При рассмотрении функции F

}

необходимо принять во внимание еще

один аспект, а именно вопрос об аппроксимации фурье-образа &р

. По-

скольку мы рассматриваем данные, получаемые в процессе физического

эксперимента, значения р

аппроксимируют лишь величины радоновского

образа функции изображения /, которое нам необходимо реконструиро-

156

ГЛАВА

вать.

Можно записать функцию

виде

Ре

= ®ef +

Щ,

№.46)

где

[Я, Л(0

[#/](^ 0). (8.47)

Из определения преобразования Фурье (8.27) следует,

что для

всех

спра-

ведливо соотношение

l&PeW = l&#

fW) + l^rieWl

(8.48)

Поскольку

rig

представляет собой

шум,

содержащийся

исходных дан-

ных,

то

можно рассматривать амплитуду шума

на

частоте

(\[&n

$U)$

как выборку случайного процесса (гл.

особенно разд. 3.1), причем ожида-

емая величина этой выборки примерно одинакова

на

всех частотах

другой стороны,

для

достаточно плавной функции

величина

\[&&P

f\(U)\

становится малой

при

стремлении

С/1

частоте 1/2*/. Следо-

вательно, величины [&p

](U) вблизи частоты 1/2*/,

как

правило, обуслов-

лены

большей степени действием шумов,

чем

преобразованием Радона

реконструируемой функции. Этот фахт также повлиял

на

введенное выше

разделение функций

на

сворачивающую

интерполяционную.

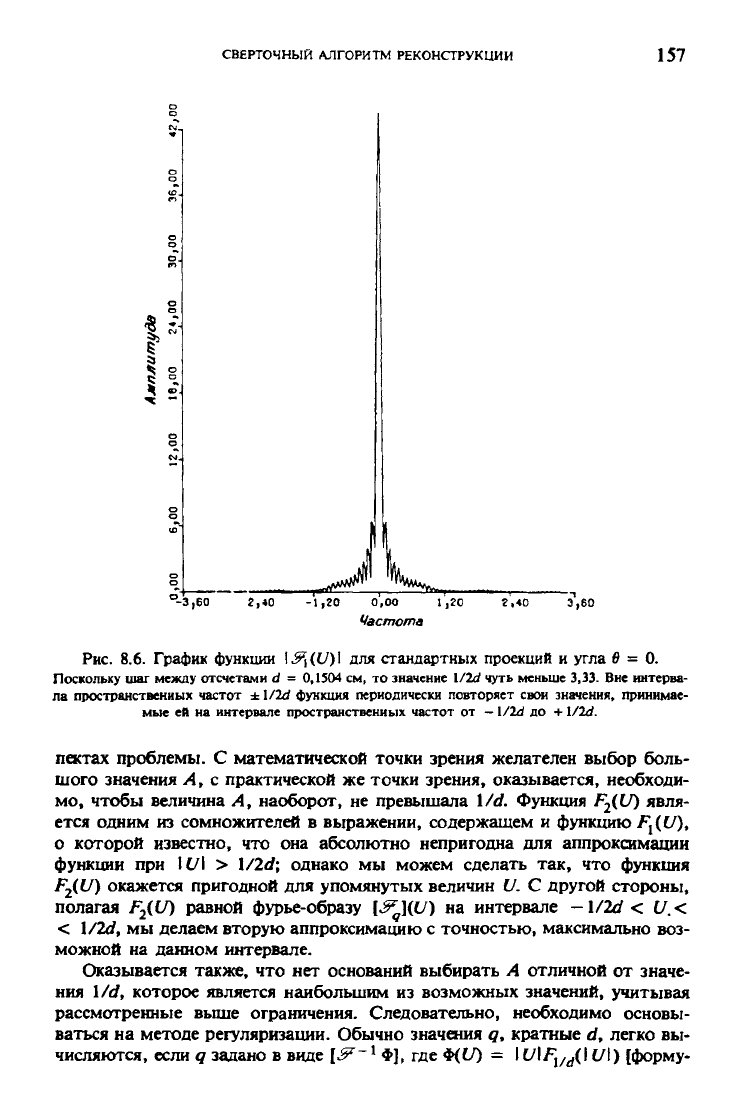
Вид функции

изображен

на

рис.

8.6, на

котором представлена зависи-

мость \F

{

(U)\

для

угла

б =

Ои

стандартных проекций, полученных

в па-

раллельном пучке

Оказывается,

что

функция

определяемая формулой (8.42), связана

функцией

соотношениями того

же

вида,

что и

функции

F, и

, однако

первом случае ситуация гораздо проще, поскольку функцию

можно

вы-

брать

по

своему усмотрению.

В первом приближении функцию

можно выбрать постоянной величи-

ной

на

полосе частот,

не

превышающей величины

\/d.

Если

это

условие

выполнено,

то при

\U\ < \/2d

имеем тождество

для

вида

(U)

l&q](U\

(8.49)

не

аппроксимированные значения

для

по

формуле (8.45).

Анализ, проведенный

разд.

8.4,

показывает,

что

сворачивающая функ-

ция (рассматриваемая

не

точки зрения проблемы регуляризации, изло-

женной

разд.

8.1

8.2)

действительно ограничена

по

частоте.

самом

деле, фурье-образ

является функцией, определяемой соотношением

(8.31).

Если

мы

выбираем величину

А,

не

превышающую

\/d

то

тожде-

ство (8.49) справедливо.

Теперь

мы

должны разрешить дилемму следующего рода: ранее

мето-

де регуляризации предполагалось,

что

величина

должна быть

по

воз-

можности большой,

то

теперь говорим

об ее

уменьшении

до

величины

1/d.

Это противоречие возникло потому,

что мы

говорим

двух различных

ас-

СВЕРТОЧНЫЙ АЛГОРИТМ РЕКОНСТРУКЦИИ

157

1 °

* ю-

"-3,60

2,40

-1,20 0,00 1,20

Частота

2,40

Э,60

Рис. 8.6. График функции \&\(U)\ для стандартных проекций и угла 0 = 0.

Поскольку шаг между отсчетами 4 = 0,1504 см, то значение 1/24 чуть меньше 3,33. Вне интерва-

ла пространственных частот ±1/24 функиия периодически повторяет свои значения, принимае-

мые ей на интервале пространственных частот от -1/24 до +1/24.

пектах проблемы. С математической точки зрения желателен выбор боль-

шого значения А, с практической же точки зрения, оказывается, необходи-

мо,

чтобы величина А, наоборот, не превышала \/d. Функция F

(U) явля-

ется одним из сомножителей в выражении, содержащем и функцию F

(U)

о которой известно, что она абсолютно непригодна для аппроксимации

функции при \U\ > l/2d; однако мы можем сделать так, что функция

(U) окажется пригодной для упомянутых величин U. С другой стороны,

полагая F

(U) равной фурье-образу l^](U) на интервале -l/2d < U,<

l/2d

мы делаем вторую аппроксимацию с точностью, максимально воз-

можной на данном интервале.

Оказывается также, что нет оснований выбирать А отличной от значе-

ния 1/сГ, которое является наибольшим из возможных значений, учитывая

рассмотренные выше ограничения. Следовательно, необходимо основы-

ваться на методе регуляризации. Обычно значения q

кратные d

легко вы-

числяются, если q задано в виде \&~

Ф], где Ф(Ц) = IU\F

l/d

(\U\) [форму-