Хермен Г. Восстановление изображений по проекциям: Основы реконструктивной томографии

Подождите немного. Документ загружается.

168

ГЛАВА 9

Рис.

9.1.

Гармоническая функция двух полярных координат

(г,

ф)

пространствен-

ной частотой

R и

направлением

Ф,

зафиксированная

на

линии

(ф

Ф), является

гармонической функцией переменной

г с

пространственной частотой

На любой линии, перпендикулярной L н описываемой уравнением г cos(4> - Ф)= г

, значения

гармонической функции двух полярных координат постоянны.

Теперь теорему

проекциях можно записать

форме операторного

со-

отношения вида

= &

£. (9.6)

Таким образом, вычисление двумерного фурье-образа сводится

преобра-

зованию Радона,

затем

операции вычисления фурье-образа

по

первой

переменной. Теорема

проекциях непосредствен© вытекает

из

определений

преобразований Фурье

Радона. Детали доказательства

мы

опускаем.

9.2.

ФУРЬЕ-АЛГОРИТМ РЕКОНСТРУКЦИИ

Из выражений

(9.3) и

(9.6) видно,

что

для функции/двух полярных

ко-

ординат имеет место равенство вида

f =

F**f-

(9.7)

показывающее принципиальную возможность использования фурье-

алгоритма реконструкции.

Для

любой функции

р,

описывающей исходные

проекции изображения,

мы

вычисляем его

помощью следующего выраже-

ния:

.*~

^r'-F

(9.8)

Основная трудность

использовании фурье-алгоритма возникает

при

его применении

реальным исходным данным. Рассмотрим этот процесс

поэтапно.

ДРУГИЕ АЛГОРИТМЫ РЕКОНСТРУКЦИИ

169

Напомним об использованном нами предположении о том. что при ре-

гистрации исходных данных в параллельном пучке функция р известна в

точкал с координатами (nd

тД), где — N

^n^NuO^m^M—

1. Для

произвольной пространственной частоты R величину l

p](R, тА) можно

рассчитать по формуле (9.5) и в сочетании с соотношениями (9.7) и (8.27)

получить

p](R.mA)= Г р(/,юД)ехр[-2л/Я/] d/. (9.9)

Здесь мы используем тот факт, что функция р

(£) = 0 при If

> Е.

Интеграл в правой части (9.9) необходимо вычислить при некоторых

выбранных значениях R. Замена интеграла римановой интегральной сум-

мой,

взятой в точках отсчета, дает

0>р](Я, тД) ~ г/ X р(л^шД)ехр[-2я!Ди</]. (9.10)

FI=-/V

В действительности данная аппроксимация верна лишь в ограниченном

диапазоне пространственных частот /?, поскольку выражение в правой ча-

сти (9.10) имеет вид

(R)= £ №р](ЛтЫтД). (9.11)

к=

-со

Использование в этой формуле такого же обозначения F

что и в соотно-

шении (8.41) и последующем анализе разд. 8.6, не является случайным. Не-

трудно показать, что функция, определенная с помощью равенства (9.11),

тождественна введенной в гл. 8 функции F

Как это уже обсуждалось в

разд.

8.6, функциюF

(R) можно аппроксимировать фурье-обраэом \&

p\ х

х (/?, тД) (= lFp

^](R)) при \R

l/2rf,

но даже в этом интервале про-

странственных частот она может быть неточной, особенно вблизи границ

интервала. На пространственных частотах \R\ >

l/2d

вероятно, лучше

полагать

[^ур](/?,

тА) равным нулю, чем пользоваться формулой (9.10).

Мы также должны сделать предположение относительно точек R в ин-

тервале

—

\/2d ^ R ^ l/2d, в котором мы собираемся вычислять значе-

ния

[^ур](/?,

тА). С точки зрения выполнения вычислений желательно (по

причинам, которые мы здесь упомянем) отобрать величины R, которые

кратны значениям

1/(27V

+ l)d. Заметим, что последнее не является реаль-

ным ограничением на плотность расположения точек отсчета, поскольку

вычисления по формуле (9.10) не изменяются, если мы пожелаем восполь-

зоваться ей при больших N. [Напомним, что p{nd, тД) = 0 при nd > £.]

С учетом приведенных выводов можно утверждать, что первым этапом

фурье-алгоритма является вычисление величины

p](w'/(2/V

+ l)d, тА)

170

ГЛАВА 9

по формуле

p](ri/(2N

\)(LmA)

- d £

'rind.

/пЛ)ехр[-2я/ш?'

(2N + 1)].

(9.12)

при

0 ^ m < Л/ - 1 и N ^ п' ^ N.

Сумма

правой части (9.12)

точностью

до d

представляет собой

так

называемый дискретный фурье-образ

по

первой переменной

от

дискретизи-

рованной функции

р.

Введем следующее обозначение:

[®&

p\(n\ т) = £ РШ, wA)exp[ -2ninri/(2N + 1)].

(9.13)

л= -N

Расчет значений ~Ш*

в M(2N + 1)

точках

при 0 < т < Л/ - 1 и

—

N < л' < N

гораздо менее трудоемок, чем

это

может показаться

на

пер-

вый взгляд. Заметим прежде всего,

что как и в

сверточном алгоритме,

здесь

мы

имеем дело

каждым ракурсом отдельно.

27V +

1 различных зна-

чений [^^

р\(п',

т)

при фиксированном

т и

переменной

п'

вычисляются

по

1 значениям функции p(nd

тА) при тех же

значениях

тип. Так как

величины

exp

[

—

2irinn'/(2N

+ 1)]

можно вычислить заранее

занести

память ЭВМ

(так как они не

зависят

от

исходных данных),

то

вычисления

по формуле (9.13)

при

фиксированном

т и

изменяющемся

п'

требуют

вы-

полнения

2(2N + I)

операций умножения. (Множитель

появляется из-за

того,

что

каждый член суммы вещественных чисел умножается

на

ком-

плексное число,

и это

требует двух операций умножения.) Однако имеется

гораздо более эффективный способ вычислений

по

формуле (9.13)

при

—

N < п' < N, чем

метод, рассчитывающий данное выражение раздельно

для каждого значения

п'.

Упомянутый алгоритм носит название быстрого

преобразования Фурье (БПФ).

Его

рассмотрение выходит

за

рамки данной

книги, однако здесь необходимо проанализировать характеристики данного

алгоритма, поскольку

они

весьма существенны

при

оценке эффективности

фурье-алгоритма реконструкции изображений.

С использованием алгоритма БПФ расчет

по

формуле (9.13) потребует

(при фиксированном значении

т для

всех

2N + 1

значений

л',

лежащих

интервале

от

—

N до N)

приблизительно

N(3 +

log

N I)

операций умно-

жения,

где

riog

yv1 есть наименьшая

из

целых величин, превышающая

log

Рассмотрим случай регистрации стандартных проекций

параллельном

пучке

для М = 144 и N = 82. При

этом непосредственные вычисления

по

формуле (9.13) потребуют 2M(2N

+ I)

7840800

= 8 •

операций

ум-

ножения, тогда

как при

использовании алгоритма

БПФ их

потребуется

только

MN(3 +

flog

N"l)

118080

= 10

, т.е.

имеет место уменьшение

объема вычислений

на

весьма существенную величину

в два

порядка.

В се-

рийных сканерах,

где

число отсчетов

может

во

много

раз

превышать

ДРУГИЕ АЛГОРИТМЫ РЕКОНСТРУКЦИИ

171

рассмотренные в нашем примере величины, экономия вычислений может

быть еще более существенной.

Таким образом, с использованием алгоритма БПФ первый этап вычис-

лений по формуле (9.13) при 0 ^ т ^ М - 1и -N^ л' ^ N можно реа-

лизовать с относительно малыми затратами машинного времени.

Теперь мы сталкиваемся с проблемой расчета JJ"

p по вычисленным

значениям &

p в точках [n/(2N + l)d, тА]. Один из возможных путей ре-

шения этой проблемы состоит в использовании предположения о том, что

[^уР](Я.

тА) при \R\ ^ Е наилучшим образом аппроксимируется нуле-

вым значением, что в сочетании с представлением интеграла интегральной

римановой суммой дает расчетное значение в изображении, т.е.

д М-1 N

£1V "Г I

n=-N

(2N 4 \)d

[ЯУурУът)

x exp 2ni — r cos(0 - шД) . (9.14)

В фурье-алгоритме реконструкции этот способ обычно не используют

по причинам чисто вычислительного характера. Возвращаясь к рассмотрен-

ному выше примеру с фантомом головы, исследованным методом стан-

дартных проекций в параллельном пучке, мы видим, что оценка/* получе-

на в У-точках (У = 115 х 115 = 13225). Если формулу (9.14) применять

раздельно в каждой точке, то полное требуемое число операций умножения

составит величину порядка 2JM(2N + 1) > 6 • 10

, даже если мы будем

считать, что значения

ехр 2л/ — — г cos(0 - тА)

2/V + 1

(2N + IVI 4 (2/V + \)d

вычислены заранее и занесены в память ЭВМ. Подобный объем вычисле-

ний чрезвычайно велик с учетом того, что в использованном примере он

гораздо меньше, чем в серийных сканерах, в которых этот объем по край-

ней мере на порядок больше. Чтобы еще раз показать нецелесообразность

вычислений по формуле (9.14), оценим полное число операций умножения,

необходимых для реализации сверточного алгоритма в случае реконструк-

ции фантома головы в параллельном пучке с использованием стандартных

проекционных данных. Как в этом можно убедиться, их полное число ле-

жит в пределах 10

— 10

в зависимости от используемого метода интерпо-

ляции, однако этот объем в любом случае примерно на два порядка мень-

ше,

чем при расчетах по формуле (9.14).

Очевидно, что необходимо найти другой метод расчета величин

p по значениям F

p в точках с координатами {n/(2N + \)d, тА),

Один из путей решения этой проблемы состоит в разбиении вычислений

по формуле (9.14) на два этапа, а именно:

172

ГЛАВА 9

а) для каждого т, лежащего в интервале 0 ^ т ^ М - 1, вычисляем

(n'd,

тА) при

—

N ^ п' ^ N с помощью выражения

(9.15)

б) функцию /* (г, ф) вычисляем по формуле

М- I

/ *(г, </>) = Д £

Гк

(

cos(</> - шД), тА). (9 16)

Последняя операция включает в себя интерполяцию значений p

{r cos (ф

—

— тА), тА) по величинам р

(л'd, тА).

Данный подход практически идентичен сверточному алгоритму, за ис-

ключением того, что функция р

определяется соотношением (9.15), а не

(8.23).

Действительно, соотношение (9.15) можно переписать в виде дис-

кретной свертки функции р со сворачивающей функцией q, и поэтому толь-

ко что рассмотренный подход полностью тождествен сверточному алго-

ритму (по этой причине он больше не будет упоминаться в этой главе).

Рассмотрим теперь эффективную альтернативу упомянутого выше алго-

ритма, которая также является фурье-алгоритмом, но в нем используют

быстрое двумерное преобразование Фурье. Эту разновидность алгоритма

БПФ используют для вычисления двумерного обратного фурье-образа

.^"'FB

У-точках по значениям F, взятым также в У-точках. Число требуе-

мых операций умножения составит в этом случае величину порядка

log

(поточечное вычисление интегральных римановых сумм, как это было уже

установлено, требует У

операций умножения).

Трудности, связанные с этим способом вычислений, состоят в том, что

точки, в которых рассчитываются значения J^

- l

F , и точки, в которых не-

обходимо взять значения F, должны лежать на эквидистантной прямо-

угольной сетке [например, в центрах ячеек w-элементной сетки (разд.

4.1)].

Для наших приложений это не является ограничением, если дело касается

выходного изображения, поскольку нам необходимо вычислить величину

/* = &f

p для точек, находящихся в центрах ячеек. Иначе обстоит де-

ло с входными данными. Первая стадия фурье-алгоритма дает нам значе-

ния в точках с координатами [n/(2N + \)d, тА)

лежащих на концентриче-

ских окружностях, а не на прямоугольной сетке (рис. 9.2).

Таким образом, фурье-алгоритм реконструкции, помимо уже рассмот-

ренной выше первой стадии, имеет еще две. Вторая стадия предусматрива-

ет вычисление значений 3*

р в точках на прямоугольной сетке с использо-

ванием величин &

p, полученных на первой стадии (т.е. на радиальной сет-

ке).

На третьей стадии используется алгоритм БПФ для получения функ-

ции /* в центрах ячеек. Детальное рассмотрение двух последних стадий

выходит за рамки данной книги, однако здесь мы упомянем некоторые

особенности, которые встречаются при разработке фурье-алгоритма и

обеспечивают приемлемое качество реконструкции.

ДРУГИЕ АЛГОРИТМЫ РЕКОНСТРУКЦИИ

173

,1/(2N+I)d

Я)

ы\1

т Т Т "^

■4-

-* +■

Рис. 9.2.

о — вид координатной сетки, на которой вычисляются значения /

p\ б — вид координатной

сетки, в узлах которой необходимо знать величины функции, прежде чем вычислять обратное

двумерное БПФ.

Основная трудность обусловлена тем, что алгоритм БПФ позволяет

вычислить лишь двумерный обратный фурье-образ. Соотношение между

выходными данными после БПФ и истинными значениями обратного

фурье-образа аналогичны соотношению, связывающему функцию F,, опре-

деленную соотношением (9.11), и фурье-образ &Р

±- В частности, если

расстояние между точками, в которых производится интерполяция значе-

ний ^ур, равно 6 (рис. 9.2), то выходные данные после БПФ могут быть

достаточно точными в прямоугольной области, ограниченной соотношени-

ями lrcos<£l < 1/26 и

г sin ф

< 1/26. Более того, вблизи границ обла-

сти возможно ухудшение данных вследствие возникновения ложных про-

странственных частот (разд. 8.6). Таким образом, для получения рекон-

струируемых изображений приемлемого качества нам необходимо выбрать

величину 6 достаточно малой, так, чтобы обратная ей величина 1/6 > Е.

Последнее требование приводит к двум нежелательным для вычислений

последствиям.

Во-первых, операцию БПФ необходимо применять в точках, число ко-

торых намного превышает число ячеек в реконструированном изображении

J и которые соответствуют дополнительным ячейкам, вводимым при заме-

не области изображения с размерами Е х Е на область с размерами

1/6 х 1/6. Подходящее увеличение числа ячеек может быть не больше чем

в 9 раз (если 1/6 = ЗЕ), что существенно снижает вычислительную эффек-

тивность алгоритма БПФ и, кроме того, накладывает дополнительные

требования на объем памяти ЭВМ. Во-вторых, для получения точных зна-

чений &ур на прямоугольной сетке с размером ячейки 6 можно вычислить

величину .?ур на первой стадии процесса в точках с координатами

174

ГЛАВА 9

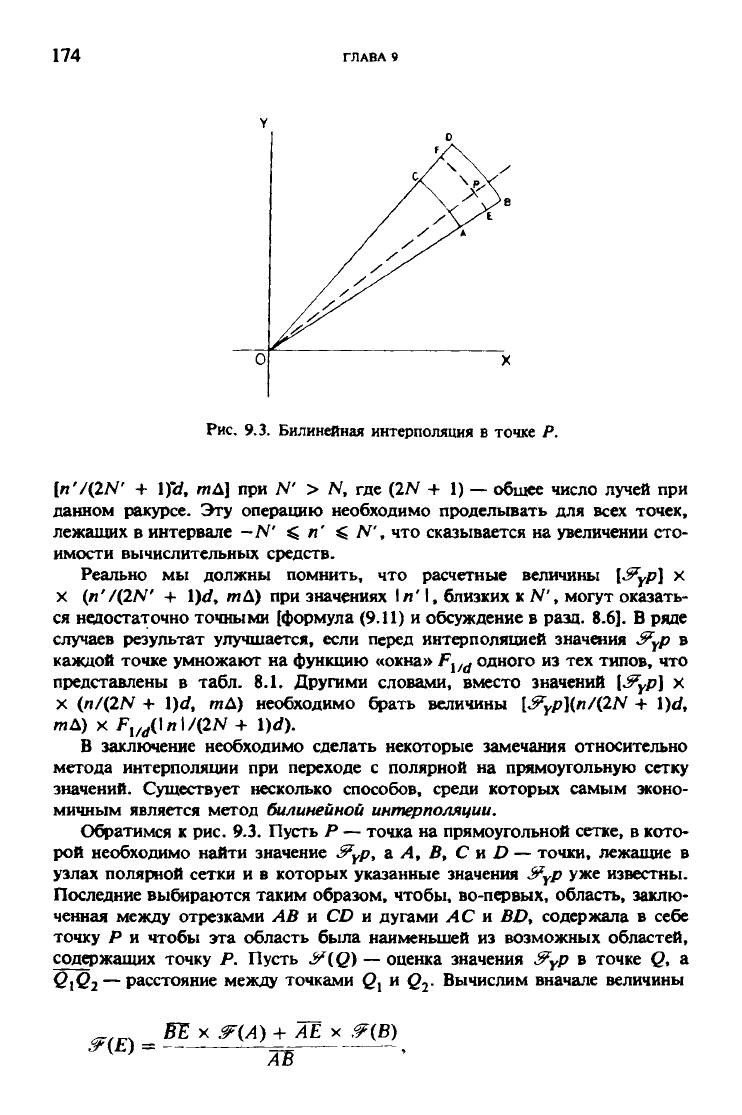
Рис. 9.3. Билинейная интерполяция в точке Р.

[w'/(2N' + 1)7/, т&\ при N' > N, где (2N + 1) — общее число лучей при

данном ракурсе. Эту операцию необходимо проделывать для всех точек,

лежащих в интервале —N' ^ п' ^ N', что сказывается на увеличении сто-

имости вычислительных средств.

Реально мы должны помнить, что расчетные величины [&ур]

х (л'/(2ЛГ' + 1)</, тД) при значениях \п' I, близких к N', могут оказать-

ся недостаточно точными [формула (9.11) и обсуждение в разд. 8.6]. В ряде

случаев результат улучшается, если перед интерполяцией значения &

р в

каждой точке умножают на функцию «окна» F

x/d

одного из тех типов, что

представлены в табл. 8.1. Другими словами, вместо значений \&

p\ х

х (n/(2N + \)d

глД) необходимо брать величины [&

p](n/(2N + \)d

тД) х F

l/d

(\n\/(2N + \)d).

В заключение необходимо сделать некоторые замечания относительно

метода интерполяции при переходе с полярной на прямоугольную сетку

значений. Существует несколько способов, среди которых самым эконо-

мичным является метод билинейной интерполяции,

Обратимся к рис. 9.3. Пусть Р — точка на прямоугольной сетке, в кото-

рой необходимо найти значение ^ур, а Л, В, С и D — точки, лежащие в

узлах полярной сетки и в которых указанные значения &

р уже известны.

Последние выбираются таким образом, чтобы, во-первых, область, заклю-

ченная между отрезками АВ и CD и дугами АС и BD, содержала в себе

точку Р и чтобы зга область была наименьшей из возможных областей,

содержащих точку Р. Пусть &(Q) — оценка значения &

р в точке Q, а

— расстояние между точками Q

и Q

. Вычислим вначале величины

ДРУГИЕ АЛГОРИТМЫ РЕКОНСТРУКЦИИ

175

DF х ¥{С) + CF х &ф)

W> = ~ ^ • (9.17)

Обозначим через РЁ (соответственно через PF) длину дуги, соединяющую

точки Р и Е (соответственно Р и F). Тогда

РЁ х &(F) +

х &(Е)

ПП = ji+pp • (9Л8)

Характеристики фурье-алгоритма реконструкции при использовании

стандартных проекционных данных, полученные в параллельном пучке, ил-

люстрируются рис. 9.4 и 9.5, а также табл. 9.1. Были произведены две ре-

конструкции, в одной из которых двумерный обратный фурье-образ вычис-

лялся с помощью алгоритма БПФ в J - 115 х 115 точках, на первой ста-

дии было принято N

= TV, а число лучей в одном ракурсе составляло

27V + 1 = 165. При второй реконструкции была предпринята попытка

уменьшить эффект возникновения ложных частот путем выбора массива из

345 х 345 точек для алгоритма обратного двумерного БПФ. Размер увели-

ченной области реконструкции стал, таким образом, равным 51,888 см (на-

помним, что размер элиза составляет 0,1504 х 0,1504 см), поэтому

6 =

1/51,888

= 0,0193. Мы стремились подобрать значение N' таким, что-

бы

\/(2N'

+ \)d <

для получения требуемой точности интерполяции на

второй стадии. Мы использовали

TV'

= 244. В обоих реконструкциях перед

интерполяцией производилось поточечное перемножение вычисленной ве-

личины &ур со значением функции обобщенного «окна» Хэмминга при

а = 0,8. Это позволяет сравнивать данные результаты с результатами, по-

Таблица

9.1

Мера расстояния между изображениями

для реконструированных изображений рис. 9.4

115 х 115 0,2780 0,1747 0,1417 Неприемлемо

345 х 345 0,1100 0,0524 0,0592 »

Затраты машинного времени / считаются неприемлемыми, поскольку из-за ограниченно-

го объема оперативной памяти ЭВМ типа Cyber 173 реконструкция рассматриваемых изображе-

ний производилась иа яругой ЭВМ.

176

ГЛАВА 9

Рис. 9.4 Рис. 9.5

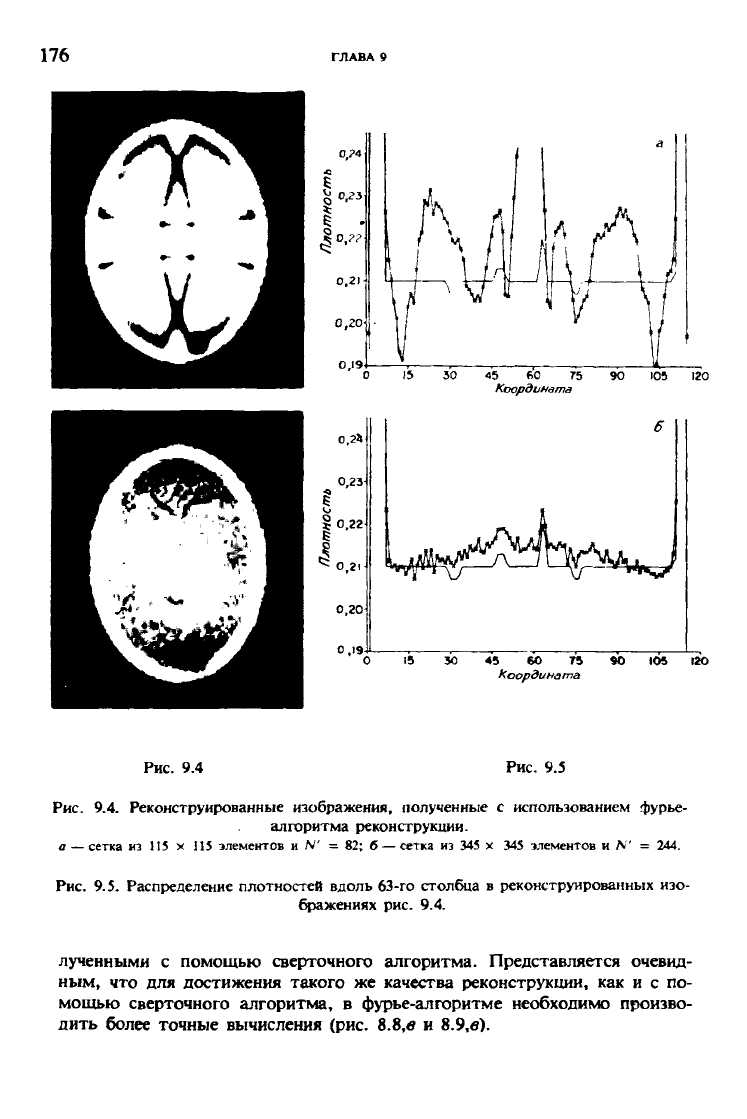
Рис. 9.4. Реконструированные изображения, полученные с использованием фурье-

алгоритма реконструкции.

а — сетка из 115 х 115 элементов и N' — 82; б — сетка из 345 х 345 элементов и Л" = 244.

Рис. 9.5. Распределение плотностей вдоль 63-го столбца в реконструированных изо-

бражениях рис. 9.4.

лученными с помощью сверточного алгоритма. Представляется очевид-

ным,

что для достижения такого же качества реконструкции, как и с по-

мощью сверточного алгоритма, в фурье-алгоритме необходимо произво-

дить более точные вычисления (рис. 8.8,в и 8.9,в).

ДРУГИЕ АЛГОРИТМЫ РЕКОНСТРУКЦИИ

177

9.3.

АЛГОРИТМ р-ФИЛЬТРАЦИИ ОБРАТНОГО ПРОЕЦИРОВАНИЯ

При рассмотрении метода непрерывного обратного проецирования от-

мечалось, что последний дает размытые изображения исходных картин,

причем вклад исходной картины в точке А в реконструированное изображе-

ние в точке В обратно пропорционален расстоянию между этими точками.

Назначение алгоритма, описываемого в данном разделе, состоит в том,

чтобы ликвидировать нерезкость в изображении, возникающей в процессе

обратного проецирования.

Указанный алгоритм основан на соотношении между двумерными

фурье-образами изображения и радоновского образа того же изображения,

подвергнутого обратному проецированию. Это соотношение имеет вид

[^2Ж^ Ф) = |Л

х [&

ЯЯП(К

ФХ

(9.19)

в любой точке с координатами (/?, Ф) при R * 0.

Оценка изображения / по проекциям р> согласно соотношению (9.19),

распадается на четыре стадии:

а) обратное проецирование р для получения величины &р\

б) вычисление двумерного фурье-образа &

&р\

в) получение новой функции F двух полярных координат согласно выра-

жению

F(R

Ф) = |Я| х |\^

ЭД(Я, Ф). (9.20)

г) оценка изображения по формуле

/♦ = ^2^. (9.21)

Этимология названия алгоритма на английском языке такова: нередко ре-

зультаты обратного проецирования в литературе называют слоеграммой

(layergram). В статье, где были сформулированы особенности этого алго-

ритма, первая полярная координата в двумерном фурье-образе обознача-

лась греческой буквой р, поэтому указанные выше операции «б» — «г» по-

лучили наименование р-фильтрации.

Недостатком рассматриваемого алгоритма являются трудности в его

применении, которые последовательно будут рассмотрены ниже.

Достаточно легко вычислить величину &р в любой точке с координата-

ми

(г,

ф),

используя при

этом

выражения для интегральной римановой суммы и

интерполяцию согласно раэд. 7.2. Однако заметим, что, даже если функция

р( (

в) = 0

при

\ t \ ^ Е,

все равно не

существует значения£", для которого

было бы справедливо соотношение

[^р](г,

ф) = 0 при г > £".

Другими словами, существует случай (можно самостоятельно доказать

это),

когда

lim sup [ЗД(г, ф) = 0, (9.22)