Хермен Г. Восстановление изображений по проекциям: Основы реконструктивной томографии

Подождите немного. Документ загружается.

108

ГЛАВА 6

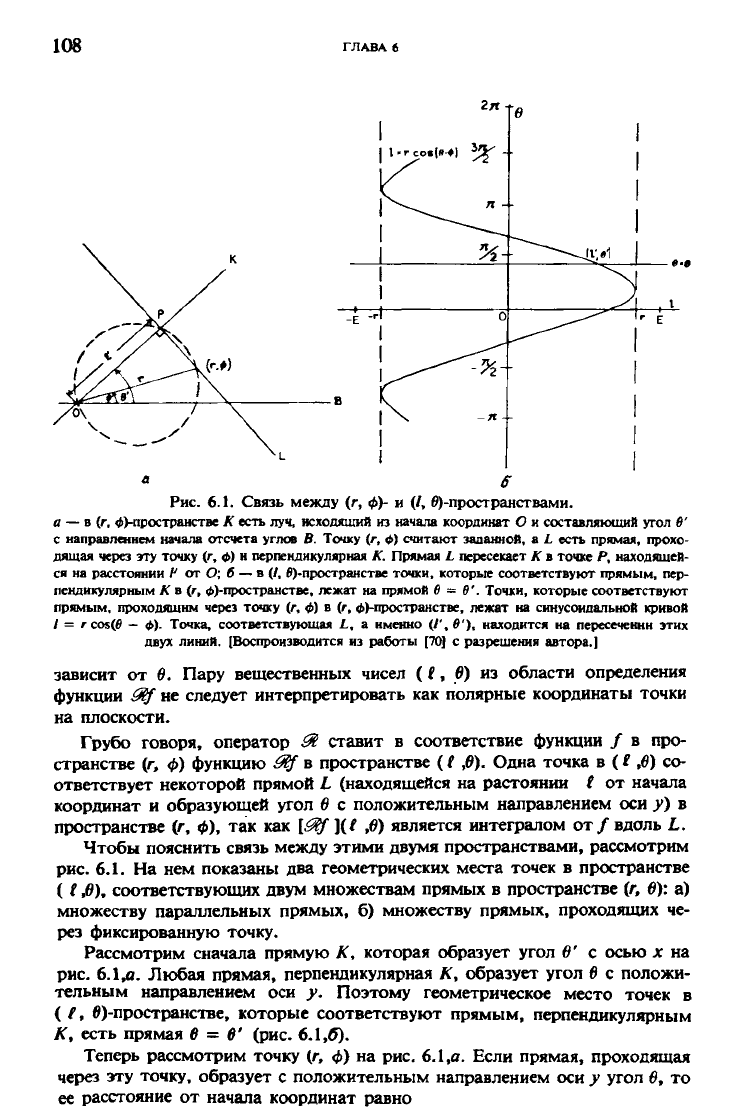
Рис. 6.1. Связь между (г, ФУ и (/, ^-пространствами.

а — в (г, ^Пространстве К есть луч, исходящий из начала координат О и составляющий угол в'

с направлением начала отсчета углов В Точку (г,

Ф)

считают заданной, a L есть прямая, прохо-

дящая через эту точку (г, ф) н перпендикулярная К. Прямая L пересекает К в точке Я, находящей-

ся на расстоянии V от О; б — в (/, ^-пространстве точки, которые соответствуют прямым, пер-

пендикулярным К в (г, ^-пространстве, лежат на прямой в - в'. Точки, которые соответствуют

прямым, проходящим через точку (г, ф) в (/-, ^-пространстве, лежат на синусоидальной кривой

/ = rcos(0 - ф). Точка, соответствующая L, а нменно (/', 0'), находится на пересеченнн этих

двух линий. [Воспроизводится из работы [70] с разрешения автора.]

зависит от 0. Пару вещественных чисел ((, 0) из области определения

функции &f не следует интерпретировать как полярные координаты точки

на плоскости.

Грубо говоря, оператор @ ставит в соответствие функции / в про-

странстве (г, ф) функцию (Щ в пространстве (t ,0). Одна точка в (t ,0) со-

ответствует некоторой прямой L (находящейся на растоянии t от начала

координат и образующей угол 0 с положительным направлением оси у) в

пространстве (г, ф), так как \@f ](£ ,0) является интегралом от/ вдоль L.

Чтобы пояснить связь между этими двумя пространствами, рассмотрим

рис. 6.1. На нем показаны два геометрических места точек в пространстве

(t ,0), соответствующих двум множествам прямых в пространстве (г, 0): а)

множеству параллельных прямых, б) множеству прямых, проходящих че-

рез фиксированную точку.

Рассмотрим сначала прямую К

которая образует угол 0' с осью х на

рис. 6.1,я. Любая прямая, перпендикулярная К, образует угол 0 с положи-

тельным направлением оси у. Поэтому геометрическое место точек в

( е

0)-пространстве, которые соответствуют прямым, перпендикулярным

есть прямая 0 = 0' (рис. 6.1,6).

Теперь рассмотрим точку (г, ф) на рис. 6.1,а. Если прямая, проходящая

через эту точку, образует с положительным направлением оси у угол 0, то

ее расстояние от начала координат равно

ОСНОВНЫЕ ПРЕДСТАВЛЕНИЯ ОБ АЛГОРИТМАХ РЕКОНСТРУКЦИИ

109

*? = Г COS(0 - ф).

(6.7)

Поэтому геометрическое место точек в ( i ,0)-пространстве, которому соот-

ветствуют прямые, проходящие через точку (г, ф), есть кривая, описывае-

мая уравнением (6.7), см. рис. 6.1,6.

Точка в (f ,0)-пространстве, которая соответствует прямой L, являю-

щейся перпендикуляром к К (и поэтому составляющей угол в' с положи-

тельной полуосью у) и в то же время проходящей через заданную точку (г,

ф\ есть точка (rcos(0' - <р), 0').

Входные данные алгоритма реконструкции представляют собой оценки

(основанные на физических измерениях) значений \@f ](1,0) для конечного

числа пар ( £ ,0), а выходные данные являются оценками значений в опреде-

ленном смысле функции /. В этой главе дано точное разъяснение этого ко-

роткого описания.

Пусть оценки \&f ]( i ,0) известны для / пар (£ ,, 0,), ( (

, 0

), ...,(£

). Определим &uf для 1 ^ / ^ / выражением

■*,-/ =[*/](/„0,).

(6.8)

Я"

I 1 t

*/2\

—тА

-2А

(nd,mu)

Nd~E

d 2d nd £ Nd

-Я/2

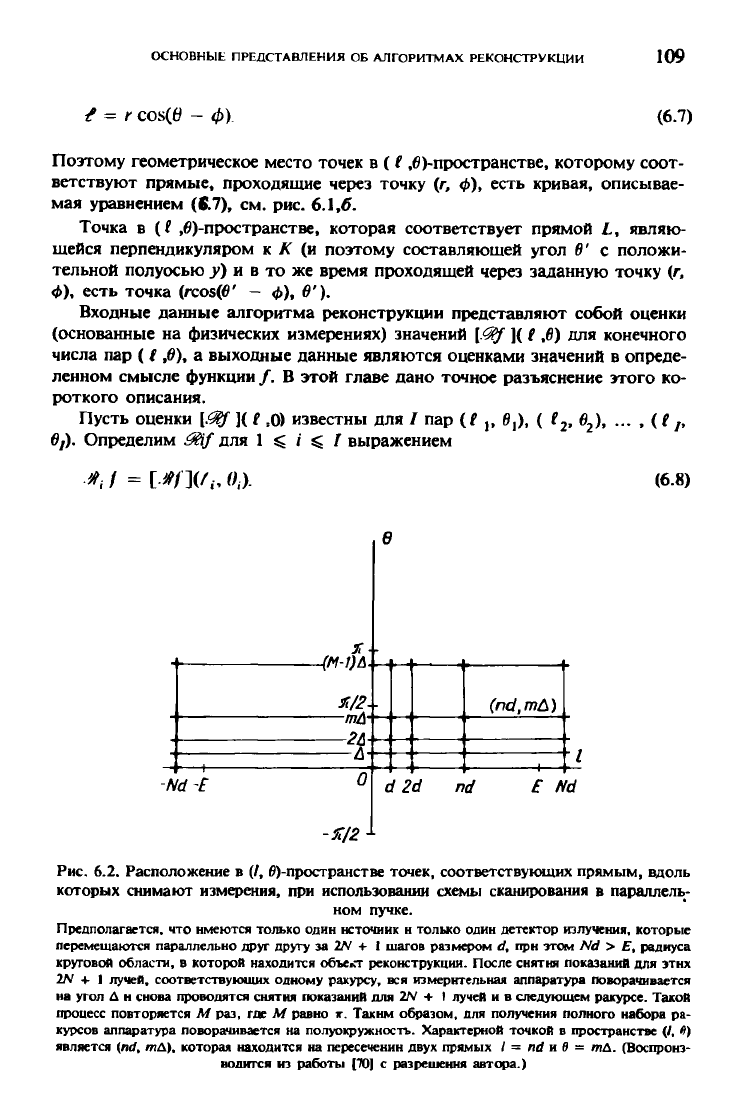
Рис. 6.2. Расположение в (/, ^-пространстве точек, соответствующих прямым, вдоль

которых снимают измерения, при использовании схемы сканирования в параллель-

ном пучке.

Предполагается, что имеются только один источник

только один детектор излучения, которые

перемещаются параллельно друг другу

за

2/V

1 шагов размером

прн этом

Nd > £,

радиуса

круговой области,

которой находится объект реконструкции. После снятия показаний для этих

2/V

-I- 1

лучей, соответствующих одному ракурсу, вся измерительная аппаратура поворачивается

на угол

Д н

снова проводятся снятия показаний для 2/V

+ f

лучей

и в

следующем ракурсе. Такой

процесс повторяется

раз,

где М

равно

ж.

Таким образом, для получения полного набора

ра-

курсов аппаратура поворачивается

на

полуокружность. Характерной точкой

пространстве

(/, в)

является

(nd, тА),

которая находится

на

пересечении двух прямых

/ = nd и в

—

тА.

(Воспроиз-

водится

из

работы [70]

разрешения автора.)

по

ГЛАВА 6

&i — пример функционала; результат его действия на функцию есть ве-

щественное число. В дальнейшем, если не оговорено, мы обозначим через

имеющиеся оценки

&&f,

а для обозначения /-мерного вектора-столбца ис-

пользуем у, где /-й элемент такого вектора есть у

Назовем этот вектор у

вектором измерения.

При построении алгоритма реконструкции мы предполагаем, что метод

сбора данных и, следовательно, набор (< i

в,),..., ((

)) зафиксиро-

ван и известен. Кратко говоря, задача состоит в том, чтобы по эада-

ным значениям у оценить изображение /.

В двух следующих разделах уы рассмотрим основные подходы, кото-

рые используют при оценивании/. Как правило, оценка/обозначается/*.

&&J

равно значению &f в определенной точке (£,, 0

) в пространстве

(I ,0). При использовании любой геометрии сбора данных мы имеем ко-

нечное множество точек (I,, 0), в которых значения Щ/ известны. Напри-

мер,

при использовании первой и второй схем сканирования, рассмотрен-

ных в гл. 3 (схемы параллельного сканирования; см. рис. 3.3,а и б), точки

(t;, 0,), для которых значения Щ/ известны, образуют прямоугольную сет-

ку, как показано на рис. 6.2. Соответствующие расположения в методе сбо-

ра данных с веерным лучом (рис. 3.3,в и г) имеют более сложный вид; они

будут рассмотрены в гл. 10.

6.2. АЛГОРИТМЫ, ОСНОВАННЫЕ

НА ИСПОЛЬЗОВАНИИ ПРЕОБРАЗОВАНИЙ

Один из способов определения оценки f функции / состоит в том, что-

бы дать формулу, которая выражает значения

/*(г> Ф)

через величины г, ф,

У\>

— . У г Такая формула может быть «дискретизированной» версией об-

ратного преобразования Радона, которое описывает / по ее ралоновскому

образу 3$ . Алгоритмы, основанные на таком подходе, называют алго-

ритмами с преобразованием. В остальной части данного раздела мы при-

ведем более детальное объяснение того, что было сказано выше.

Преобразование Радона ставит в соответствие функции / двух полярных

переменных другую функцию

&Pf

двух переменных. Все, что мы ищем, это

оператор

&t~

такой, что

&t~

Щ приводил к / (т.е. при его действии на

данную функцию

&Pf

получалась бы функция /). Точно так как выражение

(1.4) описывает, каким образом определяется значение &f для любой пары

действительных чисел (f ,0) по значениям/, принимаемым этой функцией в

области ее задания, нам нужна формула, которая по функциям от двух ве-

щественных переменных р определяет Prf в точках (г,

ф).

Такой формулой

является

D*"

"рКг.

ф)

= L Г С

]

Л|

(/,

0) d<

d0.

(6.9)

2я

rcos(tf - ф) -е

где р

(1 ,0) обозначает частную производную

от

р(1,0) по / . [См. также

ОСНОВНЫЕ ПРЕДСТАВЛЕНИЯ ОБ АЛГОРИТМАХ РЕКОНСТРУКЦИИ 111

(6.2) гл. 2).] В разд. 16.3 будет показано, что для любой функции изображе-

ния двух полярных переменных / (которая удовлетворяет некоторым физи-

чески разумным условиям)

&Р~

3?f = / в том смысле, что для всех точек

(г,

ф) справедливо

№-**№.

ф)

= f

(г.

ф).

(6.Ю)

Для того чтобы понять сущность оператора ^~

выразим его в виде

последовательности простых операторов.

Обозначим взятие частной производной по первой переменной функции

двух вещественных переменных через &

. Тогда для любой функции р двух

вещественных переменных для любой пары вещественных чисел (£ ft)

в предположении, конечно, что предел правой части этого выражения су-

ществует.

В нашем случае функция/?, на которую действует -0

, есть радоновский

образ функции изображения. Довольно легко функцию изображения / мож-

но выбрать такой, что @

(Щ не определена для всех значений (( ft). Та-

ким примером является функция изображения, которая имеет одинаковые

значения во всех точках внутри кадра изображения. Можно строго матема-

тически определить $

так, что этот оператор имеет смысл и в подобных

ситуациях. Здесь же мы просто предположим, что для любой функции изо-

бражения /, которое хотим восстановить, правая часть выражения (6.11)

определена для р = Рл$. Следующий оператор, который нам надо

ввести, — это оператор преобразования Гильберта

<%f^q

по

отношению к

первой переменной функции двух переменных д. Для любой пары вещест-

венных чисел ( i', В) определим

[*гЙЛ

в) = - - Г ^°] d/.

(6.12)

Отметим, что интеграл в этом выражении является несобственным, так

как подынтегральная функция расходится при f = С. Его можно преоб-

разовать в интеграл в смысле главного значения Коши, т.е.

В нашем случае q — yrol&y&Pf для некоторой функции изображения/. Мы

опять положим, что для изображений, которые нам надо восстанавливать,

предел правой части выражения (6.13) существует.

И наконец, введем важный оператор, который называется оператором

обратного проецирования. Заданной функции t от двух переменных ставит-

112

ГЛАВА 6

ся

соответствие другая функция

двух полярных переменных, значения

которой

любой точке

(г, ф)

определяются следующим образом:

[.Л](г,

ф) = f t(r cos(0 - ф\ 0) dll

(6.14)

Из рис.

6.1

видно,

что

обратное проецирование функции

/ в

данной точке

(г,

ф)

получается путем интегрирования

t по

сегменту кривой

(от в = 0 до

= *")»

уравнение которой задано выражением (6.7).

Почему этот оператор назван обратным проецированием, объясняется

следующим образом.

Обратимся

прямой

К на рис.

6.1,д, которая образует угол

0' с

поло-

жительным направлением оси

х.

«Проекция» функции двух переменных

на

данную прямую

есть функция одной переменной, полученная путем инте-

грирования

вдоль прямой, перпендикулярной

К.

Другими словами,

это

есть [3?f\(t

ft'),

рассматриваемая как функция только

Прямая

кото-

рая проходит через точку

(г,

Ф)

перпендикулярна

К и

пересекает прямую

в точке

Я,

которая находится

на

расстоянии

— г cos (6'

- ф) от

начала

координат.

Теперь рассмотрим обратный процесс. Прежде

чем

находить

3% из/

путем интегрирования (проецирования) вдоль линий, таких, как

получим

для произвольной функции двух переменных

другую функцию

.Л

размы-

тием (обратным проецированием) значений вдоль таких линий. Для фикси-

рованного значения

(определяющего данную прямую) вклад

от / в &t

одинаков для всех точек

(г,

ф)

лежащих

на

одной

и той же

прямой

пер-

пендикулярной

К.

Величина вклада пропорциональна

1(1', 0'), где

—

расстояние

L от

начала координат.

Так

как

проходит через точку

(г,

ф), а К

проходит через начало координат,

то

траектория точки

Р, в ко-

торой

эти

взаимно перпендикулярные прямые пересекаются

при

изменении

0', есть окружность, диаметр которой равен расстоянию

от

начала коорди-

нат

до

этой точки

(г, ф).

Комбинируя (6.11), (6.12)

(6.14), получаем функцию

р от

двух перемен-

ных

и для

любой точки

(г, ф):

1**у'ЛР](г.ф)~- ,' ' dfdO.

(6.15)

Л Jo J ос '' COS(fl -</>)-/

Тождественность правых частей выражений

(6.9) и

(6.15)

точностью

до

постоянного множителя можно кратко выразить операторным уравнени-

ем:

» ' = -

.*.#у(/у.

(6.16)

Обратное преобразование Радона

для

функции двух переменных может

быть сведено

следующей последовательности операций:

ОСНОВНЫЕ ПРЕДСТАВЛЕНИЯ ОБ АЛГОРИТМАХ РЕКОНСТРУКЦИИ 1 13

а) взятию частной производной р по его первой переменной для полу-

чения функции q\

б) преобразованию Гильберта для q по его первой переменной для полу-

чения функции /;

в) обратному проецированию /;

г) умножению полученного результата всех этих операций на (— 1/2тг).

Этот последний процесс иногда называют нормировкой.

Последовательность этих операций предполагает, что известно точное

значение р( {,0) для всех £ и в и что требуемые операции можно выпо-

лнить точно. Ни одно из этих допущений не удовлетворяется, когда мы ис-

пользуем ЭВМ для вычисления функции по экспериментально полученным

проекционным данным. Методы преобразования для реконструкции изо-

бражений основываются на выражении (6.16) или иа альтернативных экви-

валентных выражениях для обратного преобразования Радона ^~

, но их

приходится выполнять по конечному числу «неидеальных» эксперименталь-

ных данных в условиях ограниченных возможностей современных ЭВМ.

Как это делают, будет изложено в следующих главах. Сущность того, что

надо сделать, заключается в построении вычислительных операций (кото-

рые могут быть выполнены на цифровых ЭВМ), которые приводят к оцен-

ке значений двойных интегралов, подобных тому, как находят правую

часть выражения (6.9) по данным значениям р( £,, #,) при 1 ^ / ^ /.

6.3.

АЛГОРИТМЫ РЕКОНСТРУКЦИИ,

ОСНОВАННЫЕ НА РАЗЛОЖЕНИИ ФУНКЦИИ В РЯД

Чтобы выполнить обратное преобразование Радона, были использова-

ны методы математического анализа, о котрых шла речь в последнем раз-

деле, посвященном решению проблемы реконструкции изображения. При

этом обратное преобразование Радона описывается операторами над функ-

циями, заданными на всем континиуме вещественных чисел. Для реализа-

ции обратного преобразования Радона на ЭВМ мы должны заменить не-

прерывные операторы дискретными, которые воздействуют на функции,

имеющие конечное число компонент. Это выполняется в самом конце про-

цедуры вывода алгоритма реконструкции.

Подход, основанный на разложении функции в ряд, принципиально

иной.

Дискретизацию здесь выполняют в самом начале: оценка функции

сводится к нахождению конечного множества чисел. Это производится сле-

дующим образом.

Предположим, что мы зафиксировали набор J базисных изображений

(Ь]

... , bj\; их линейные комбинации приводят нас к адекватной аппрок-

симации любого изображения /, которое мы желаем реконструировать.

Примером такого подхода является п х л-дискретизация, рассмотрен-

ная в разд. 4.1. В этом случае J = п

. Мы нумеруем элементы изображения

(элизы) от 1 до У и определяем

114

ГЛАВА 6

»А.«-(о

если (г,

ф)

находится внутри/'-го

элемента изображения; (6.17)

в противном случае.

Тогда п х я-дискретизация изображения / есть изображение /, которое

определяется выражением

/>**)

Х*А(г,4>Х (6.18)

где

— среднее значение / внутри у-го элемента изображения, а краткое

«стенографическое» обозначение, используемое нами для уравнений такого

типа, имеет вид/ =

Ey-j*^.

Существуют и другие способы выбора базисных изображений; некото-

рые из них будут рассмотрены ниже. После того как базисные изображе-

ния выбраны, любую функцию/ можно представить в виде линейной ком-

бинации базисных изображений [bj] однозначно определенным выбором

коэффициентов x

1 < j^ J

как это показано в (6.18). Здесь мы использу-

ем х для обозначения вектора-столбца, у-я компонента которого есть х., и

называем этот вектор х

вектором

изображения.

Такой подход сводит проблему «вычисления функции изображения/» к

более узкой проблеме «нахождения вектора изображения х», такого, что

оценка/, определяемая выражением (6.18), близка к/, насколько позволя-

ют выбранные базисные изображения. Чтобы выполнить это условие по

возможности более точно, определим меру «близости» между двумя изо-

бражениями. Такое определение было дано в выражении (6.3).

Известное положение математического анализа позволяет сделать вы-

вод о том, что независимо от того, как выбраны базисные изображения,

для любого изображения / существует одно и только одно изображение /,

которое обладает следующими свойствами:

а)

/ есть^линейная комбинация базисных изображений;

б) если / есть линейная комбинация базисных изображений, то

difJ)<d(U

ГУ

(6.19)

Более того, если базисные изображения выбраны так, что они являются

линейно независимыми, т.е. ни одно из них нельзя выразить как линейную

комбинацию других, то существует только единственный вектор, который

приводит к/, определенной по (6.18).

Например, если базисные изображения определены выражением (6.17),

то я х л-дискретизация /

равна

/, удовлетворяющей условиям «а» и «б», а

соответствующий вектор изображения х является единственным.

В идеале метод разложения в ряд должен приводить к такому вектору

изображения /, который наиболее близок

/. Но так как эксперименталь-

ные данные не определяют / однозначно, то, как правило, ищут такой век-

тор изображения

который удовлетворяет менее эффектному, но более

ОСНОВНЫЕ ПРЕДСТАВЛЕНИЯ ОБ АЛГОРИТМАХ РЕКОНСТРУКЦИИ

115

реальному критерию оптимизации. Такие критерии оптимизации будут

рассмотрены

следующем разделе.

Для того чтобы показать, каким образом проблема реконструкции изо-

бражения превращается

дискретную задачу при помощи метода разложе-

ния функции

ряд, рассмотрим

два

свойства функционалов

определен-

ных выражением (6.8).

Первое свойство состоит

в том, что эти

функционалы являются линей-

ными.

Это

означает,

что для

любых изображений

и/

при

всех вещест-

венных числах

и с

и для 1

^ / ^ J

имеет место соотношение

•*.<<'i

/i +

<'2

h) =

<Y*.-

/i +

CiJih-

°)

которое легко доказать, если использовать определения

Щ и

Другое свойство математически менее строго.

Мы

может утверждать,

что «если/j

и/

близки друг к другу,

то

также близки

<%f

».

К со-

жалению,

при

использовании меры различия между функциями, которая

определена

(6.3), математически строгая версия указанного утверждения

не всегда является справедливой.

Тем не

менее, опираясь

на

определение

можно показать,

что

если

определена

учетом условий

«а» и «б», то

Щ} будет приблизительно такой

же, как и

^/.

Это

свойство называется

непрерывностью. Основная слабость метода разложения

в ряд

заключает-

ся

в том, что

сделанное выше предположение иногда сильно нарушается.

Объединяя указанные свойства вместе, можно показать,

что для

1 ^

i < /

.#,1 -.*,-/

= l^XjAbj-

(6.21)

Так

как

функции Ъ. задаются пользователем,

то, как

правило, выраже-

ние

&р.

можно легко вычислить аналитическими методами. Например,

случае, когда Ь: определяется выражением (6.17),

&Pf)

равно длине отрезка

прямой, проходящей

от

источника

детектору

для /-го

положения такой

пары через у-Й элемент изображения,

или,

более точно, прямой, находя-

щейся

на

расстоянии

от

начала координат

составляющей угол

по-

ложительным направлением оси

у; см. (6.8) и рис. 2.8.

Следовательно,

i,j

**ibj.

(6.22)

Напомним еще раз, что

мы используем для обозначения эксперименталь-

но измеряемой оценки

^/.

Комбинируя

это

(6.21), получаем,

что для 1

^ / ^ /

>'.-

i.i

(6.23)

7=1

Пусть

обозначает матрицу,

(/, у)-й

элемент которой равен

г,

Назо-

116

ГЛАВА 6

вем эту матрицу проекционной матрицей. Пусть е обозначает /-мерный

вектор-столбец, i-я компонента которого e

равна разности между левой и

правой частями выражения (6.23). Мы назовем его вектором погрешности.

Тогда выражение (6.23) можно переписать в форме

= Rx + е (6.24)

Таким образом, метод, основанный на разложении функции в ряд, при-

водит к следующей дискретной задаче реконструкции: основываясь на

(6.24),

по данным значениям у оценить вектор изображения х.

Если оценка, которую мы берем в качестве решения поставленной выше

дискретной реконструктивной задачи, есть вектор х*, то оценка/* изобра-

жения, которое надо реконструировать, задается выражением

/*=

£xfbj.

(6.25)

Из изложенного выше можно сделать следующее важное заключение.

Наше обоснование метода, основанного на разложении функции в ряд, не

нуждается в том, чтобы функционал ^ определялся выражением (6.8).

Требуется только, чтобы ^ удовлетворял свойству, выраженному (6.21).

Разные способы определения ^ обладают указанным свойством: схемы с

интегрированием вдоль кривых, а не вдоль прямых или даже по площадям,

например полосам, а вдоль линий потенциально имеют прямое отношение

к общей проблеме реконструкций. Главное достоинство метода с разложе-

нием функции в ряд по сравнению с алгоритмами, основанными на исполь-

зовании преобразований, заключается в том, что их можно непосредствен-

но применить к указанным более общим схемам получения эксперимен-

тальных данных.

6.4. КРИТЕРИИ ОПТИМИЗАЦИИ

В этом разделе рассмотрим критерии оптимизации, которые использу-

ются при оценке вектора изображения методом, основанным на примене-

нии разложения функции в ряд. Хотя об этом не будет сказано в явной

форме, многое из того, что будет изложено ниже, применимо при оценке

изображений алгоритмами, основанными на преобразованиях.

В выражении (6.24) вектор е не известен. В лучшем случае мы можем

считать, что вектор е' является выборкой случайной переменной. Однако в

большинстве случаев это невозможно. Простой подход в попытке решить

(6.24) состоит в том, чтобы принять в качестве первого приближения, что

е есть нулевой вектор. Это чревато опасностью: у = Rx может не иметь

решения или может иметь много решений, ни одно из которых не является

подходящим для рассматриваемой практической задачи. Тем не менее были

выработаны некоторые критерии, указывающие, какой вектор х должен

быть выбран в качестве решения (6.24).

ОСНОВНЫЕ ПРЕДСТАВЛЕНИЯ ОБ АЛГОРИТМАХ РЕКОНСТРУКЦИИ 1 17

Критерии, которые были использованы

при

решении задач реконструк-

ции,

обычно имеют следующий

вид. В

качестве решения (6.24) выбираем

такой вектор изображения

х, для

которого значение функции

{

(х)

мини-

мально,

если имеется более

чем

один вектор, который минимизирует

(х),

то

выбирают

из них тот, для

которого минимально значение некото-

рой другой функции ф

(х).

данном разделе

мы

изложим некоторые

из

предложенных методов выборов функций ф

и ф

С теоретической точки зрения заманчивым является подход, заключаю-

щийся

следующем. Пусть как вектор изображения

так и

вектор ошибки

е являются выборками случайных переменных, которые обозначим соот-

ветственно буквами

X и Е. Так как

обсуждение

разд.

1.2

ограничено рас-

смотрением только дискретных случайных переменных

(т.е. с

конечным

числом возможных исходов),

а в

качестве возможных исходов рассматри-

ваются векторы-столбцы

из

вещественных чисел,

то

здесь необходимы

до-

полнительные пояснения. [Читатель, который

не

имеет желания знако-

миться

основными положениями теории оценок Байеса, может

без

ущер-

ба пропустить этот текст

до

(6.33).]

Случайная переменная

определяется функцией плотности вероятно-

сти

х%

которая представляет собой вещественную функцию

от

7-мерных

векторов

из

вещественных чисел, являющихся возможными исходами

Эта функция плотности вероятности определена

так,

чтобы

для

любых

пар чисел

< u

< и

, ... , t j < и,

было справедливо следующее

утверждение. Вероятность того,

что

выборка

х из X

будет иметь свойство

j ^

для 1

^ i ^ ^» Р

авна

(x)dx

...dx

. (6.26)

ДЛЯ

удобства обозначения интегралы такого рода будут иногда обозна-

чаться сокращенно:

\ Рх(*) dx.

(6.27)

В соответствии

понятиями среднего значения

дисперсии, как они

бы-

ли определены

в (1.4) и

(1.5), введем понятия средний вектор

и матрица

ковариации

которые определены следующим образом:

/•00

/'* =

хр

(х) Ах, (6-28)

J or

/•ОО

Ух

= (х -

ЛхИ*

HxfPxMdx, (6.29)

J СО

где

означает вектор-строку, который равен транспонированному