Хермен Г. Восстановление изображений по проекциям: Основы реконструктивной томографии

Подождите немного. Документ загружается.

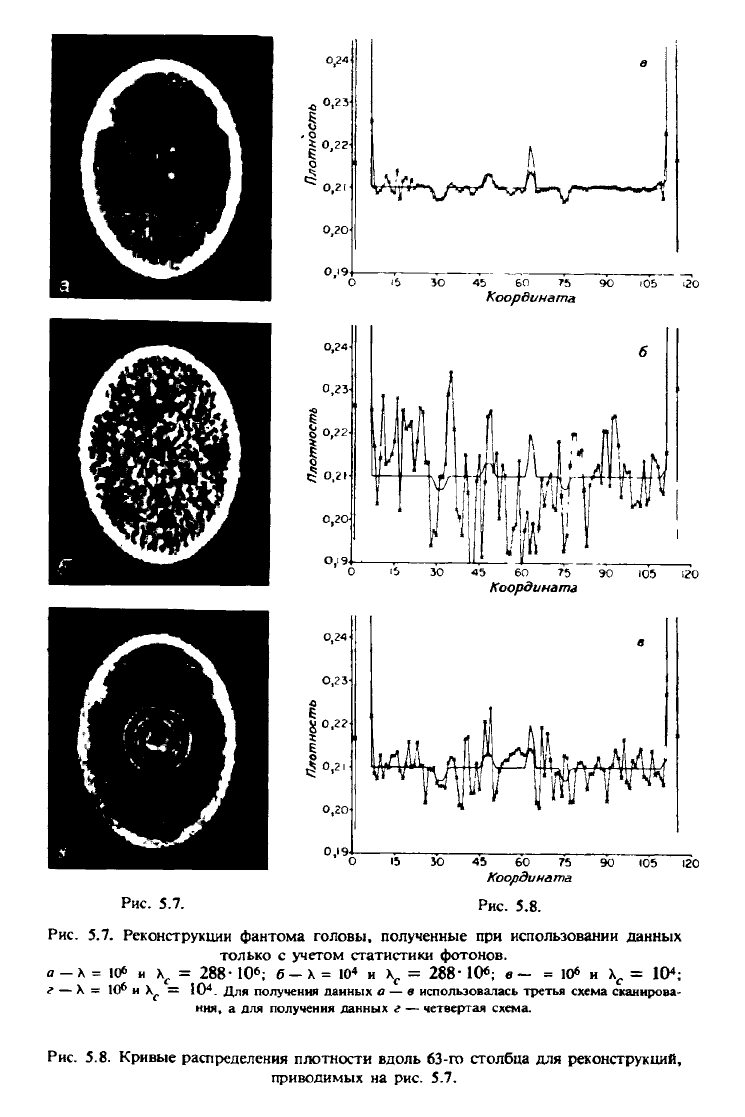
Рис. 5.7.

|о,2г

0.21

^mf^i

15 30 45 60 75 90 Ю5 i20

Координата

30 45 60 75 90 105 120

Координата

а 0.2?

^ 0,21-

0,20

0,19-

15 30

45 60 75

Координата.

Рис. 5.8.

90 «05 120

Рис. 5.7. Реконструкции фантома головы, полученные при использовании данных

только с учетом статистики фотонов.

a - X = 106

= 288- 10

; 6 - X = Ю

и Х

= 288* 10*; в - = 10* н Х

= 10

;

г -

= 10

и X

= 10

. Для получения данных a — в использовалась третья схема сканирова-

ния,

а для получения данных г — четвертая схема.

Рис. 5.8. Кривые распределения плотности вдоль 63-го столбца для реконструкций,

приводимых на рис. 5.7.

ПОЛУЧЕНИЕ ДАННЫХ И РЕКОНСТРУКЦИЯ ИЗОБРАЖЕНИЯ

W^HM^T

15 30 45 60 75 90 105 120

Координата

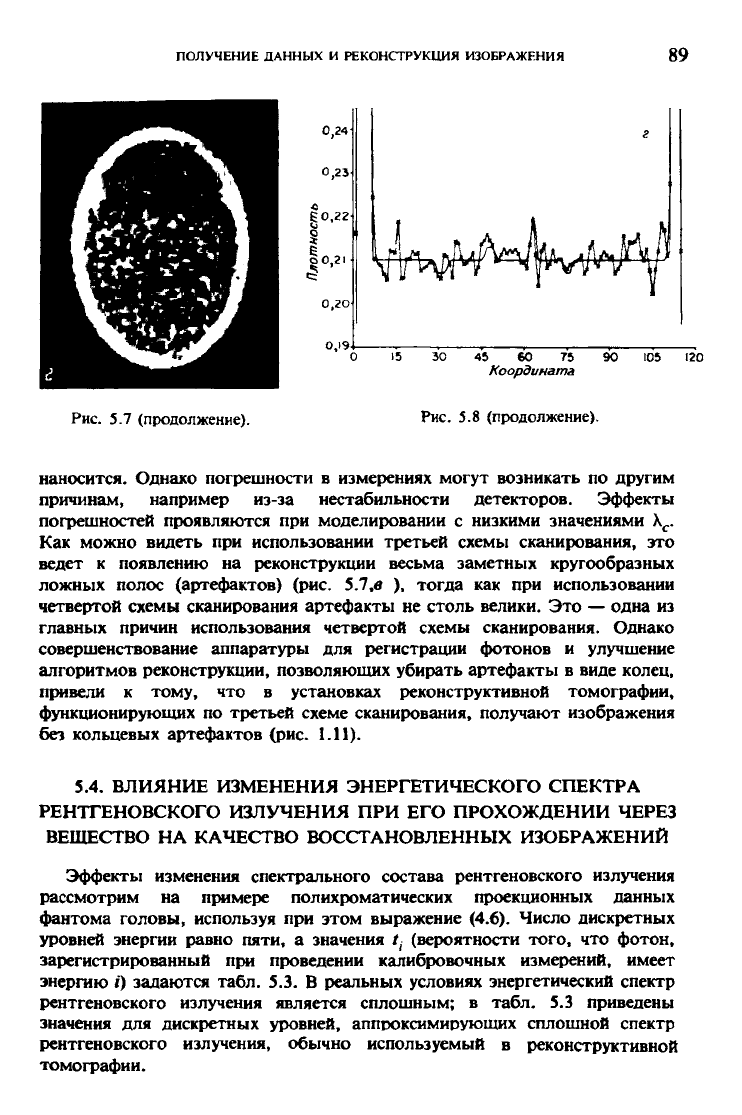
Рис. 5.8 (продолжение).

наносится. Однако погрешности в измерениях могут возникать по другим

причинам, например из-за нестабильности детекторов. Эффекты

погрешностей проявляются при моделировании с низкими значениями \

Как можно видеть при использовании третьей схемы сканирования, это

ведет к появлению на реконструкции весьма заметных кругообразных

ложных полос (артефактов) (рис. 5.7,е ), тогда как при использовании

четвертой схемы сканирования артефакты не столь велики. Это — одна из

главных причин использования четвертой схемы сканирования. Однако

совершенствование аппаратуры для регистрации фотонов и улучшение

алгоритмов реконструкции, позволяющих убирать артефакты в виде колец,

привели к тому, что в установках реконструктивной томографии,

функционирующих по третьей схеме сканирования, получают изображения

без кольцевых артефактов (рис. 1.11).

5.4. ВЛИЯНИЕ ИЗМЕНЕНИЯ ЭНЕРГЕТИЧЕСКОГО СПЕКТРА

РЕНТГЕНОВСКОГО ИЗЛУЧЕНИЯ ПРИ ЕГО ПРОХОЖДЕНИИ ЧЕРЕЗ

ВЕЩЕСТВО НА КАЧЕСТВО ВОССТАНОВЛЕННЫХ ИЗОБРАЖЕНИЙ

Эффекты изменения спектрального состава рентгеновского излучения

рассмотрим на примере полихроматических проекционных данных

фантома головы, используя при этом выражение (4.6). Число дискретных

уровней энергии равно пяти, а значения /, (вероятности того, что фотон,

зарегистрированный при проведении калибровочных измерений, имеет

энергию i) задаются табл. 5.3. В реальных условиях энергетический спектр

рентгеновского излучения является сплошным; в табл. 5.3 приведены

значения для дискретных уровней, аппроксимирующих сплошной спектр

рентгеновского излучения, обычно используемый в реконструктивной

томографии.

Рис. 5.7 (продолжение).

ГЛАВА 5

Таблица 5.3

Спектр f полихроматического рентгеновского излучения, который использовался в

описываемых экспериментах, и значения линейных коэффициентов ослабления р.

метастаза карциномы груди, соответствующие дискретным значениям энергии этого

спектра

Уровни

энергии, кэВ

0,1

0,288

2 52 0,3

0,241

3 60 0,3

0,220

4 84 0,2

0,190

5 100 0,1

0,179

Данные о размерах и расположении элементарных объектов при

использовании выражения (4.6) взяты из табл. 4.2, а величины d^,

(плотности 7-го элементарного объекта при энергии /) рассчитаны по

данным табл. 4.1. Эти полихроматические проекционные данные

вычислялись в приближении точечных источника и детекторов, в

отсутствие рассеяния и без учета статистики фотонов.

Мы хотим узнать, насколько хорошо данный фантом (основанный на

использовании значений линейных коэффициентов ослабления

рентгеновского излучения при энергии 60 кэВ) можно восстановить по

полихроматическим проекционным данным и какое улучшение в качестве

восстановления может быть достигнуто, если использовать метод

коррекции, описанный в разд. 3.2.

На рис. 5.9,0 показана реконструкция, полученная по

полихроматическим данным, а соответствующий ей график зависимости

плотности по 63-му столбцу показан на рис. 5.10,я. На рис. 5.9 видны

следы влияния линейных коэффициентов ослабления на реконструкции

внутри черепа. Это является типичным артефактом для реконструкции

изображения головной области, который связан с изменением

спектрального состава рентгеновского излучения по мере его прохождения

через вещество.

Теперь рассмотрим один из простых методов коррекции, основанный на

том,

что в области реконструкции находится всего два вида вещества.

Одним из них, естественно, должен быть воздух, так как именно он

занимает большую часть области реконструкции. Другое вещество должно

иметь характеристики ослабления рентгеновского излучения, сходные с

аналогичными характеристиками мозговой ткани, но, по всей вероятности,

ослабление в нем рентгеновского излучения должно быть немного сильнее,

чтобы учесть тот факт, что излучение проходит как через мозговую ткань,

так и костную. Среди видов ткани, данные о которых помещены в табл.

0,24

Зс

0,22

0,21

0,19

0,22

0,24

о 0.2 3

30 45 60 75 90 Ю5 120

Координата

30 45 60 75 90 Ю5 120

Координата

60 75 90

Координат*

Рис. 5.9.

Рис. 5.10.

ис.

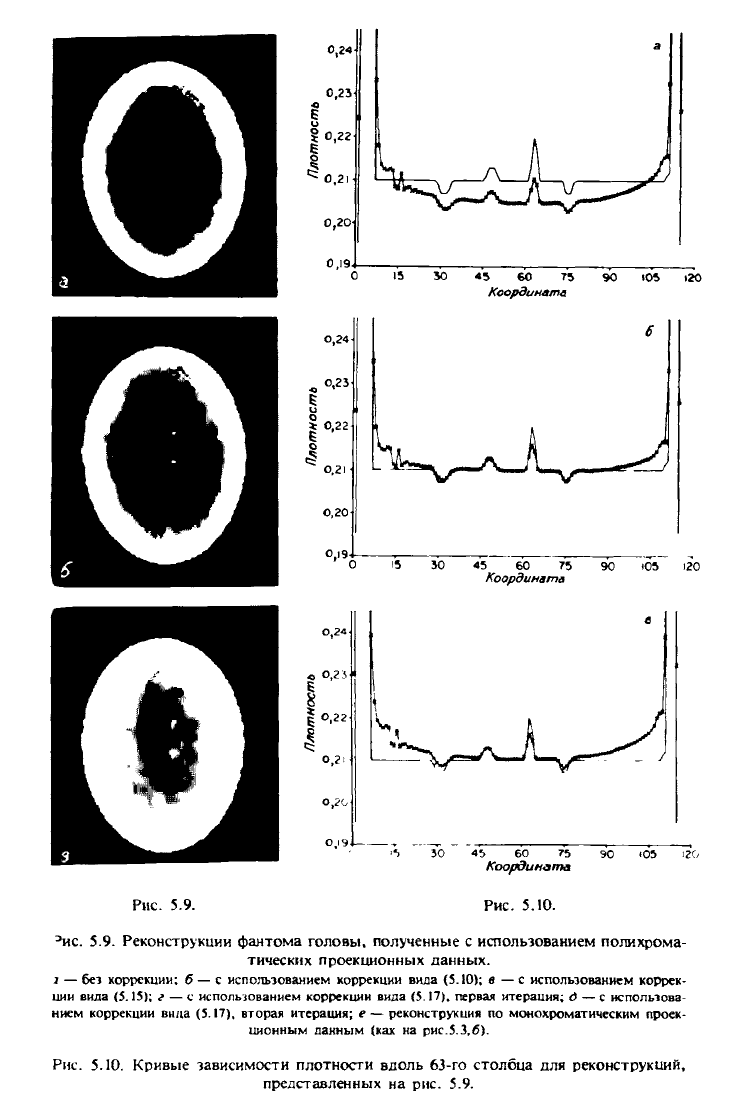
5.9. Реконструкции фантома головы, полученные с использованием полихрома-

тических проекционных данных.

1 — без коррекции;

—

использованием коррекции вила (5.10);

—

использованием коррек-

ции вила (5.15);

—

использованием коррекции вида (5.17). первая итерация;

д —с

использова-

нием коррекции вила (5.17), вторая итерация;

— реконструкция

по

монохроматическим проек-

ционным данным

(как на

рис.5.3,6).

Рис. 5.10. Кривые зависимости плотности вдоль 63-го столбца для реконструкций,

представленных на рис. 5.9.

ГЛАВА 5

* О

30 45 60 75 90 105 120

Координата

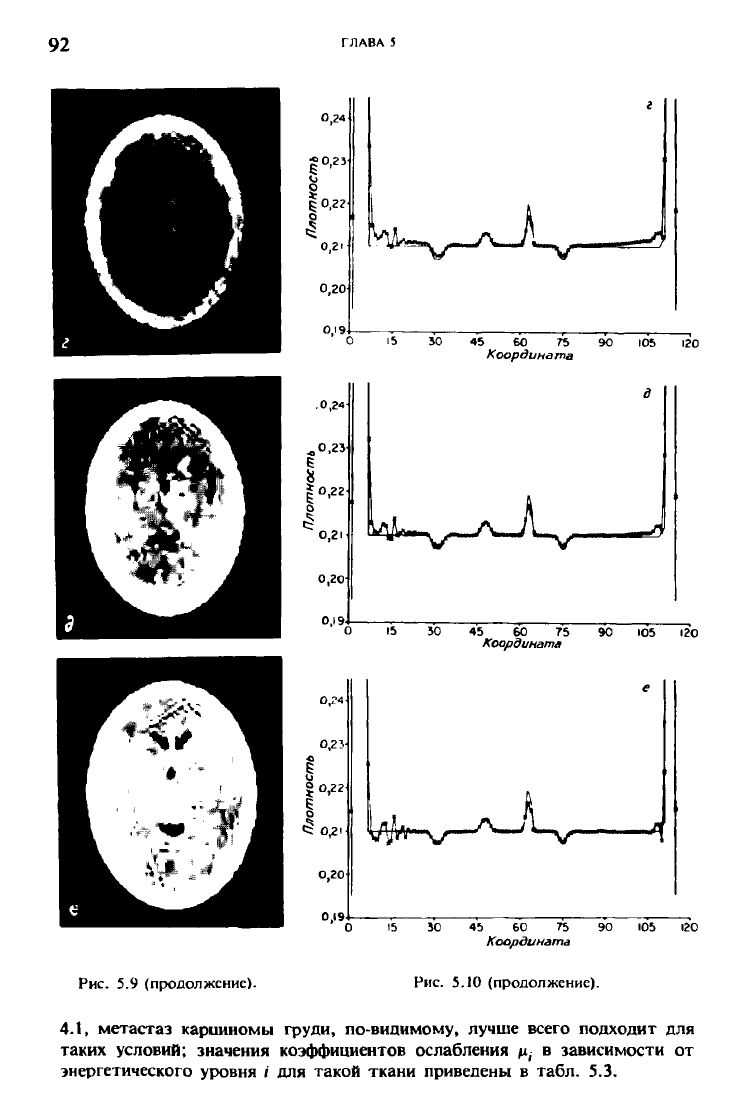
Рис. 5.9 (продолжение).

Рис. 5.10 (продолжение).

4.1,

метастаз карциномы груди, по-видимому, лучше всего подходит для

таких условий; значения коэффициентов ослабления /х, в зависимости от

энергетического уровня / для такой ткани приведены в табл. 5.3.

ПОЛУЧЕНИИ!. ДАННЫХ И РЕКОНСТРУКЦИЯ ИЗОБРАЖЬНИЯ

Используя выражение (3.14) для рассматриваемого дискретного

энергетического спектра и считая, что материалом «а» является воздух, а

материалом «б» — метастаз карциномы груди, получаем следующее

соотношение между полихроматической лучевой суммой р и монохро-

матической лучевой суммой т:

р-

-In £г

(

ехр(-

т) (5.9)

il \ /*з /

(значения /, и /x

приведены в табл. 5.3).

Полином

q'(p) = -0.000088/)

+ 0.009429/)

+ 0.9X6407/7 - 0.000022 (5.10)

является «решением» уравнения (5.9) в том смысле, что если

проанализировать спектр значений монохроматических проекционных

данных лля рассматриваемого фантома головы, то значения т находятся

между 0 и 4. Пусть

го, = 0.0001 х /\ (5.П)

p^-lni/.exp^Snl (5.12)

Другими словами, р. равно значению, правой части выражения (5.9), если т

заменить на /я

. Если вычислить т- и Pj лля у = 0, 1, . . ., 39,99 (т.е. для

n\j = 0, 0,0001, . . ., 3,9999), то получим

Ш*

™ К " 4\Pj))

= 0000060

(5ЛЗ)

V 40,000

Это значит, что для того диапазона значений m

который нас интересует,

среднеквадратичная погрешность из-за расхождения между фактическим

значением т- и величиной, полученной из соотношений (5.10), равна всего

0,00006. С этой точностью (5.10) можно считать решением (5.9).

Данные результаты приводят нас к следующему методу коррекции

эффектов изменения спектрального состава рентгеновского излучения по

мере прохождения через вещество. Для луча, полихроматическая лучевая

сумма которого равна р, монохроматическую лучевую сумму оцениваем

как q'(р). Если приближение, использованное при получении (5.9), имеет

место, а именно имеются только два материала в области восстановления:

воздух и метастаз карциномы груди, то данный метод коррекции является

достаточно хорошим.

Отметим между прочим, что (5.11) подтверждает наше утверждение,

приведенное в разд. 3.2, что использование в качестве корректирующей

ГЛАВА 5

функции полиномов низкого порядка, по всей вероятности, достаточно

оправдано. Мы показали, что для объектов, состоящих из воздуха и

ограниченного количества ткани, метастаза легкого, кубическая коррекция

[п = 3 в выражении (3.15)] дает прекрасные результаты.

На рис. 5.9,6 представлена реконструкция, полученная по

полихроматическим проекционным данным, скорректированным при

помощи (5.10), а на рис. 5.10,6—соответствующий график зависимости

плотности вдоль 63-го столбца. То, что данная реконструкция хуже, чем

изображение, которое получают по монохроматическим данным (рис. 5.3,6

и 5.4), определяется тем, что приближение о наличии только двух видов

ткани в области реконструкции является слишком грубым.

Чтобы дать меру того, насколько хороша поправка на изменение

спектра рентгеновского излучения, основанная на использовании

выражения (5.10), необходимо проанализировать значения лучевых сумм,

полученных в рабочих измерениях для описанного выше фантома. В этом

случае используется 288 положений источника и 165 положений детекторов,

или полное число лучей

520.

Пронумеруем эти лучи некоторым образом,

и пусть т+# р+ обозначают монохроматические и полихроматические

лучевые суммы соответственно для у-го луча (1 < у < 47520).

Количественная мера качества коррекции определяется тем фактом, что

/IF.

520

(

'"'' - «W

= 0.050593. (5.14)

47,520

Следует отметить, что правая часть выражения (5.14) значительно

больше правой части выражения (5.13). Теперь необходимо найти такой

полином q, что если его использовать вместо q' в выражении (4.6), то

правая часть этого выражения будет такой же малой, как и при

использовании любой другой полиномной функции вместо q. Находим, что

полином

<Др)=

1.0265/7

(5.15)

удовлетворяет этому условию. Действительно,

44j))

=0.0385: (5.16)

47,520

превосходит значение, указанное в (5.14).

Интересно отметить, что данный полином q(p) в (5.15) является

полиномом первой степени. Можно показать, что для указанного набора

данных использование полиномов более высокой степени не приводит к

существенному улучшению результата. Наилучшее, чего можно достичь

при использовании полиномов пятой степени, это снизить значение правой

части выражения (5.16) до 0,0381. Следует подчеркнуть, что это есть

ПОЛУЧЕНИЕ ДАННЫХ И РЕКОНСТРУКЦИЯ ИЗОБРАЖЕНИЯ

особенность данного сечения.

Для

других частей тела

головы,

в том

числе

и для

других сечений области головы,

при

которых значительная

часть томограммы составляет область костной ткани, было показано,

что

полиномы более высокой степени приводят

лучшим результатам.

На

рис. 5.9,в

представлена реконструкция, полученная

пс

полихроматическим данным, которые были представлены

при

помощи

выражения (5.15),

соответствующий график зависимости плотности

вдоль 63-го столбца приведен

на рис.

5.10,в.

этой реконструкции числа

Хаунсфилда очень точно воспроизводят реальные коэффициенты

ослабления рентгеновского излучения

тканях, находящихся

центральной

области. Однако

при

помощи линейных полиномов коррекции

размазывание исключить

не

удается,

так как при

такой коррекции можно

только «повысить» данные числа Хаунсфилда одновременно

для

всех

элизов.

При

поверхностном сравнении нескорректированного изображения

и изображения, скорректированного указанным методом

при

помощи

полиномов, можно прийти

выводу

о том, что

предпочтение следует

отдать первому изображению из-за

его

визуальных качеств. Такой

парадокс связан

выбором того окна, которое используют

при

отображении рисунков.

Так

как при

помощи коррекции полиномами

не

удается устранить

размазывание,

то

очередная задача состоит

нахождении другого, более

совершенного метода коррекции. Одним

из них

является итерационной

метод коррекции.

Если получены оценки

т' и р' для

моно-

полихроматических

лучевых сумм, такие,

что т'

—

q(p')

достаточно близко

к т

—

q{p\ где

—

корректирующий полином,

то

можно построить следующее

приближение

монохроматической лучевой сумме:

т ^ т

—

q(p) + q(p).

(5.17)

Сущность метода заключается

следующем. Представим данную

реконструкцию, которая является дискретизированным изображением,

помощью У-мерного вектора

х , где

— число элизов, а у-я компонента

этого вектора

есть оценка относительного линейного ослабления

в у-м

элизе

при

энергии

е.

Оценим

т'

р',

исходя

из

вектора

х.

Пусть

есть J-мерныЙ вектор

у-я

компонента которого равна длине

пересечения луча

с у-м

элизом. Учитывая

все это,

определим

псевдомонохроматическую лучевую сумму

т' как

т'

= £г-

Х/

, (5.18)

7=1

Пусть

для 1 < / ^ / и 1 ^ у < У

величина

р^

обозначает среднее

значение относительного линейного ослабления

для i-го

уровня энергии

у-м элиэе. Предполагаем,

что мы

можем, используя физическую

ГЛАВА

информацию, получить / функций q

для 1 ^ / ^ /, таких, что

УАх,)*Ц

(5-19)

Обозначая через г, вероятность того, что фотон, зарегистрированный во

время калибровки, имеет энергию /, определим псевдополихроматическую

лучевую сумму р' как

р = -In £/,схр - £/^Дх,) . (5.20)

Сравнивая выражения (5.18) и (2.4), а также (5.20) и (3.10), мы видим,

что если х дает хорошую аппроксимацию данной дискретизации

изображения, которое надо восстановить, то (5.17), вероятно, будет

справедливо. Правая часть выражения (5.17) дает новое значение

монохроматических проекционных данных, которые затем можно

использовать повторно в качестве входной информации в алгоритме

реконструкции. На рис. 5.9,г представлена реконструкция, полученная по

этим входным данным, а соответствующий ей график зависимости

плотности вдоль 63-го столбца приведен на рис. 5.10,г. Как реконструкция,

так и график показывают, насколько хорошо действует эта одноразовая

итерация. Область в центре, которая уже была достаточно хорошо

скорректирована, почти не затрагивается, тогда как ббльшая часть

размазанной области скорректирована, а граница между черепом и

мозговым веществом видна намного четче. Замечательным является тот

факт, что на снимке снова видна гематома. Сравнение этой реконструкции

с реконструкцией, полученной по монохроматическим проекционным

данным, относительно которой мы испытываем методы коррекции,

достаточно благоприятно.

Однако с улучшением качества реконструкции растет стоимость этой

реконструкции, а описанный только что метод обходится достаточно

дорого. Если коррекцию ведут при помощи полиномов., то требуется

выполнить несколько операций умножения на лучевую сумму даже для

полиномов высокого порядка. Между тем при вычислении псевдосумм

приходится выполнять большое число операций на каждый луч,

определять длину пересечения луча и элиза, а также возводить в степень.

Время, затраченное на проведение коррекции при помощи полиномов, с

одной стороны, и получения проекционных данных для одного шага итери-

рования — с другой, равно 50 и 1000 с соответственно. Несмотря на то что

в этих программах не используют специальное для реконструкций

математическое обеспечение и поэтому можно ожидать более коротких

коммерческих времен, указанные значения времени дают количественное

представление о разнице в стоимости этих двух методов коррекции.

Если считать, что заново полученная реконструкция (рис. 5.9,г) лучше

реконструкции рис. 5.9,е, то следует ожидать, что повторное вычисление

величин т' up' по этой лучшей реконструкции при помощи (5.17)

ПОЛУЧЕНИЕ ДАННЫХ И РЕКОНСТРУКЦИЯ ИЗОБРАЖЕНИЯ

0,1448

0.0723

0,0830

0,1388

0,0665 0.0777

0,1314

0,0683

0,0736

0,1082

0,0525 0,0542

0,1041

0,0486 0.0553

0,0900

0,0379

0,0517

Таблица

5.4

Мера различия изображений, полученных по монохроматическим,

полихроматическим и скорректированным полихроматическим проекционным

данным

Данные d г е

Полихроматические проекционные данные

Коррекция с использованием выражения (5.10)

Коррекция с использованием выражения (5.15)

Коррекция с использованием выражения (5.17):

первая итерация

вторая итерация

Монохроматические проекционные данные

приведет к еще более высокому качеству реконструкции. Подобная

реконструкция приведена на рис. 5.9,с), а соответствующая кривая

зависимости плотности по 63-му столбцу — на рис. 5.10,д. По сравнению с

предыдущей реконструкцией имеется лишь незначительное улучшение

качества изображения на этом рисунке. С точки зрения стоимости

дальнейшие итерации нецелесообразны.

В табл. 5.4 приведены меры различия изображений для указанных выше

реконструкций.

5.5. ВЛИЯНИЕ ГЕОМЕТРИЧЕСКИХ РАЗМЕРОВ ДЕТЕКТОРОВ

И ПРОЦЕССА РАССЕЯНИЯ ФОТОНОВ

Как было показано в разд. 3.3, кроме статистики фотонов и изменения

спектрального состава излучения по мере его прохождения через вещество,

имеется ряд других причин, почему физические измерения позволяют

получить всего лишь некоторые аппроксимации линейных интегралов от

линейного коэффициента ослабления рентгеновского излучения. В этом

разделе рассмотрим влияние на реконструкции двух из них — геометричес-

ких размеров используемых для измерений детекторов и процесса

рассеяния фотонов рентгеновского излучения.

Математический аспект процесса реконструкции, по крайней мере как на

это указывает выражение (2.5), основан на существовании линейных

интегралов от относительного линейного коэффициента ослабления

рентгеновского излучения. Конечные размеры фокального пятна источника

и детектора приводят к возникновению эффекта частично заполненного

объема, который был рассмотрен в разд. 3.3. Мы промоделировали этот

эффект для рассмотренного нами фантома головы и стандартной